考虑交通信息的PHEV电量消耗轨迹预测与跟随算法研究

王 旭，杜光乾，黄 勇，田光宇

(清华大学 汽车安全与节能国家重点实验室， 北京 100084)

由于现阶段纯电动汽车尚存在行驶里程短、电池价格高、使用寿命短、充电不方便等问题，因此发展插电式混合动力汽车(plug-in hybrid electric vehicle, PHEV)成为新能源汽车发展的重要组成部分[1-3]。从2011年到2016年，我国PHEV销量从2 580辆增长至9.8万辆， PHEV已表现出有效的节能减排能力。由于存在多个能量源且其最优工作区间不同，使得PHEV的性能与能量管理策略紧密相关。现有的策略主要是基于经验制定的规则[4-5]，其节能效果受工况的影响大，因此PHEV的燃油经济性依然存在提升空间。随着汽车智能化、网联化成为必然趋势，汽车部件及系统的控制策略可与多信息系统相结合[6]。若能将实时自车信息、道路信息以及交通信息等有效整合到PHEV的能量管理策略中，则可大幅提升PHEV的工况适应性，从而提升燃油经济性。

根据能量管理策略是否以建立数学模型为基础，PHEV的策略可以分为基于规则和基于优化两种[1，7-9]。基于规则的策略通常根据工程师的经验制定，根据其规则是否以模糊数学为基础，可以分为确定规则的策略和模糊规则的策略[5，10-13]。基于优化的策略则需要建立数学模型，利用优化方法进行求解，主要有基于极小值原理的策略[14-15]和基于动态规划(dynamic programming, DP)的策略[16-17]。DP算法将复杂问题分解为简单子问题并层层求解，是解决复杂优化问题的常见方法之一[16]。Brahma等[18]在给定工况上运用DP算法求解了串联混合动力汽车的能量管理问题。针对DP算法需要工况已知和计算量大的问题，Gong等[19]结合ITS系统提出了双尺度的DP算法，与传统的DP算法相比增加了在线应用能力，并且提升了3.7%的燃油经济性。

本文旨在利用ITS提供的多种信息设计PHEV的能量管理策略。由于目前ITS尚未完全普及，因此有必要首先搭建能获得自车、交通、道路数据的驾驶员在环仿真平台，从而为算法的研究提供基础。在研究电池电量消耗与交通拥堵等级的关系时发现二者显著相关，因此可依据交通拥堵等级预测电量消耗轨迹。首先在剩余行程的尺度上利用各路段的交通拥堵等级预测车速，通过DP算法求解得到各路段的可用电量；然后在当前路段的尺度上利用多种信息更准确地预测车速，并结合该路段的可用电量求解得到最优电量消耗轨迹；最后通过算法跟随该轨迹从而实现在线控制，并验证了算法的有效性。

1 获取ITS数据的仿真平台

由于难以获得现实中ITS的各信息，本文在清华大学汽车安全与节能国家重点实验室的模拟驾驶实验系统的基础上搭建了仿真环境进行驾驶员在环仿真实验，以期获得自车数据、交通数据和道路数据等，以便开展基于ITS的能量管理算法研究。

1.1 仿真环境

为了尽量还原真实的驾驶场景，需要搭建仿真道路环境和交通环境。前者包括道路、路口、交通指示灯以及路边景观等，本文定义了23个平均长度为3 km的路段，共22个路口。后者指行车队列中各车的运行方式，主要包括头车和跟车的车速和安全距离模型。行车队列如图1所示。

图1 行车队列示意图

1.2 仿真实验

基于上述驾驶模拟系统和仿真环境，本文设计了7条具有不同交通环境的路线并进行了驾驶员在环仿真实验，获得了对应的7组实验数据，其中每组数据包括图2中的8个信号。以下的策略研究将以该7组数据为研究基础。

图2 实验中采集的数据

图2中的交通拥堵等级的定义参照北京市交通拥堵评价体系，如表1所示，共分为5个等级，即通过计算各路段的平均车速获得其交通拥堵等级。

表1 交通拥堵等级定义

2 问题建模与求解

本文所研究的并联式PHEV的动力系统结构简图如图3所示，其工作模式包括发动机模式、纯电模式、混动模式和制动能量回收模式。为设计基于ITS的在线策略，可先利用DP算法求解全局最优解并探索规律，再设计在线自适应策略。

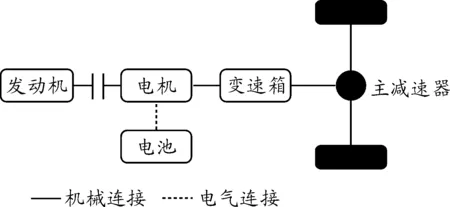
图3 并联式PHEV动力系统结构简图

2.1 能量优化问题模型

本文选取动力电池组的SOC作为状态量，驱动电机输出功率Pm(t)作为控制变量。能量优化问题的目标函数如式(1)所示。

(1)

其中：poil表示油价；Coil表示发动机的燃油消耗速率(L/h)，主要依据发动机万有特性图获得；pele表示电价；Cele=VocIb表示动力电池的耗电功率，Ib(t)为电池电流。由Rint模型有：

(2)

其中：Pb(t)为电池输出功率；Voc(t)为电池的开路电压；R(t)为电池内阻。根据SOC的定义可得其变化率为式(3)所示，其中Qb是电池的标称容量。

式(1)所示的优化问题存在的约束条件包括：始末点状态量确定的等式约束、过程中控制量和状态量因物理原因导致的不等式约束，且存在等式约束，如式(4)所示，其中Pbus为整车需求功率，Pengine为发动机的输出功率。

Pbus(t)=Pengine(t)+Pm(t)

(4)

2.2 动态规划求解

DP将复杂问题分解为简单子问题并层层求解，是解决复杂优化问题的常见方法之一。由于上述能量优化问题高度非线性，难以解析求解，但可数值求解。将式(1)改写为：

通过正向求解可以得到原问题的最优解，其求解过程如图5所示。

对实验所获得的7个线路的数据采用DP算法得到其最优SOC变化轨迹，其中线路1的最优SOC变化轨迹如图6所示。

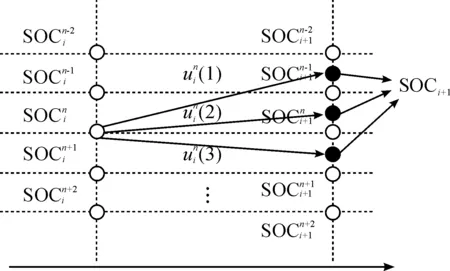
图4 动态规划倒序求解示意图

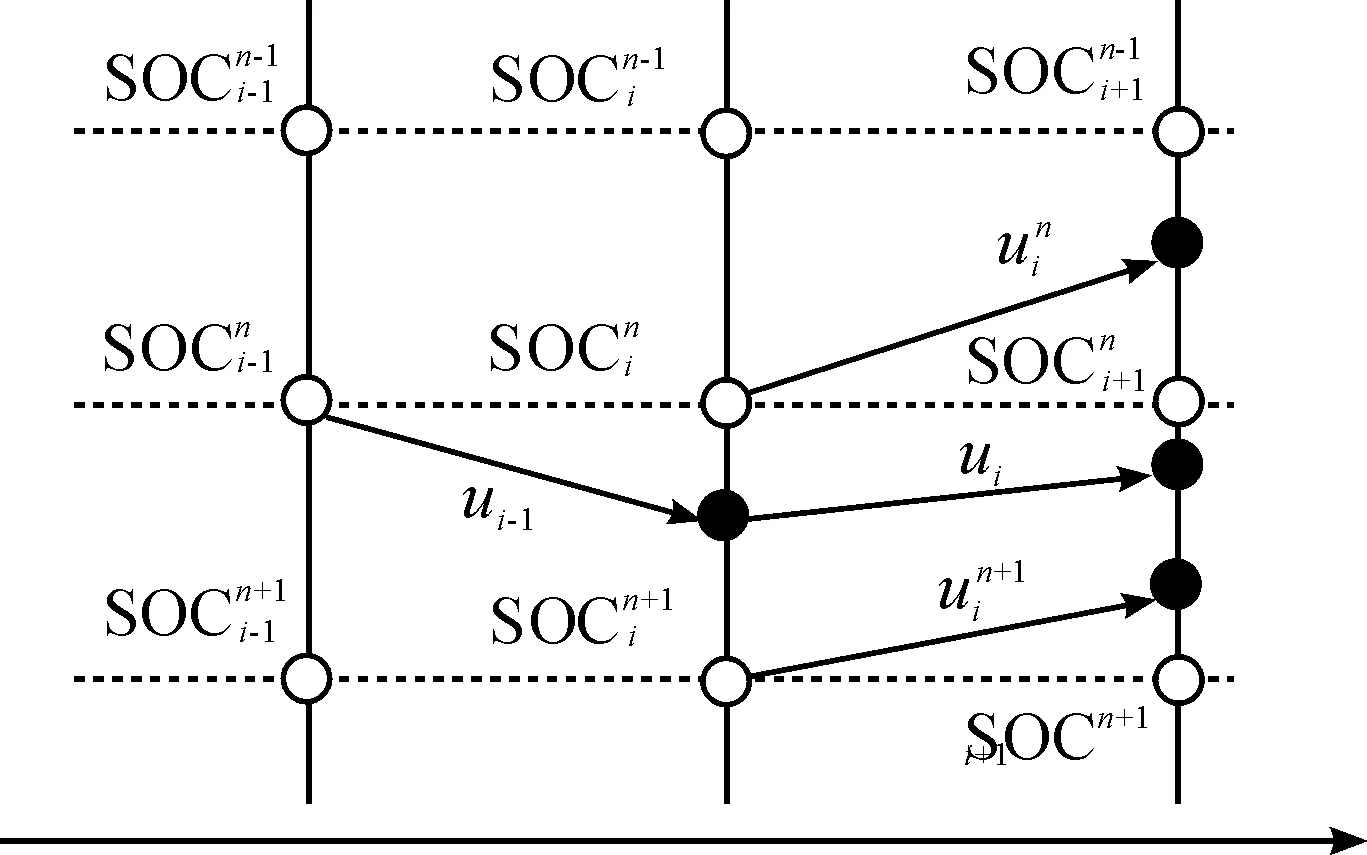
图5 动态规划正向求解示意图

图6 线路1的最优SOC变化轨迹

在利用箱线图定性分析各初始SOC下的电池电量变化速率与交通拥堵等级的关系时发现二者显著相关，以SOC0=0.9时的结果为例，如图7所示，交通拥堵等级越高，即平均车速越大，电池电量变化速率越大。再利用Spearman相关系数定量研究不同初始SOC下二者的相关性，发现相关系数均在0.612 7～0.710 7之间，进一步表明电池电量变化与交通拥堵等级之间的相关性。

3 多信息电量消耗轨迹预测算法

虽然电池电量变化与交通拥堵等级之间存在相关性，但直接根据交通拥堵等级预测电量消耗轨迹难以收敛，而车速序列是判断交通拥堵等级的依据，也是获得电量消耗轨迹的来源。因此，本文一方面利用剩余行程各路段的交通拥堵等级预测对应路段的车速，然后利用DP算法求解出剩余行程的最优电量消耗轨迹，从而得到各路段的可用电量。另一方面，利用当前路段的可用电量和多种实时信息可更准确地预测出当前路段的车速，并利用DP算法求解出当前路段的电量消耗轨迹，在线控制时则跟随该轨迹。在训练上述2个车速预测模型时，利用从仿真平台上采集的前6条线路的数据，将第7组数据用于验证算法的有效性。

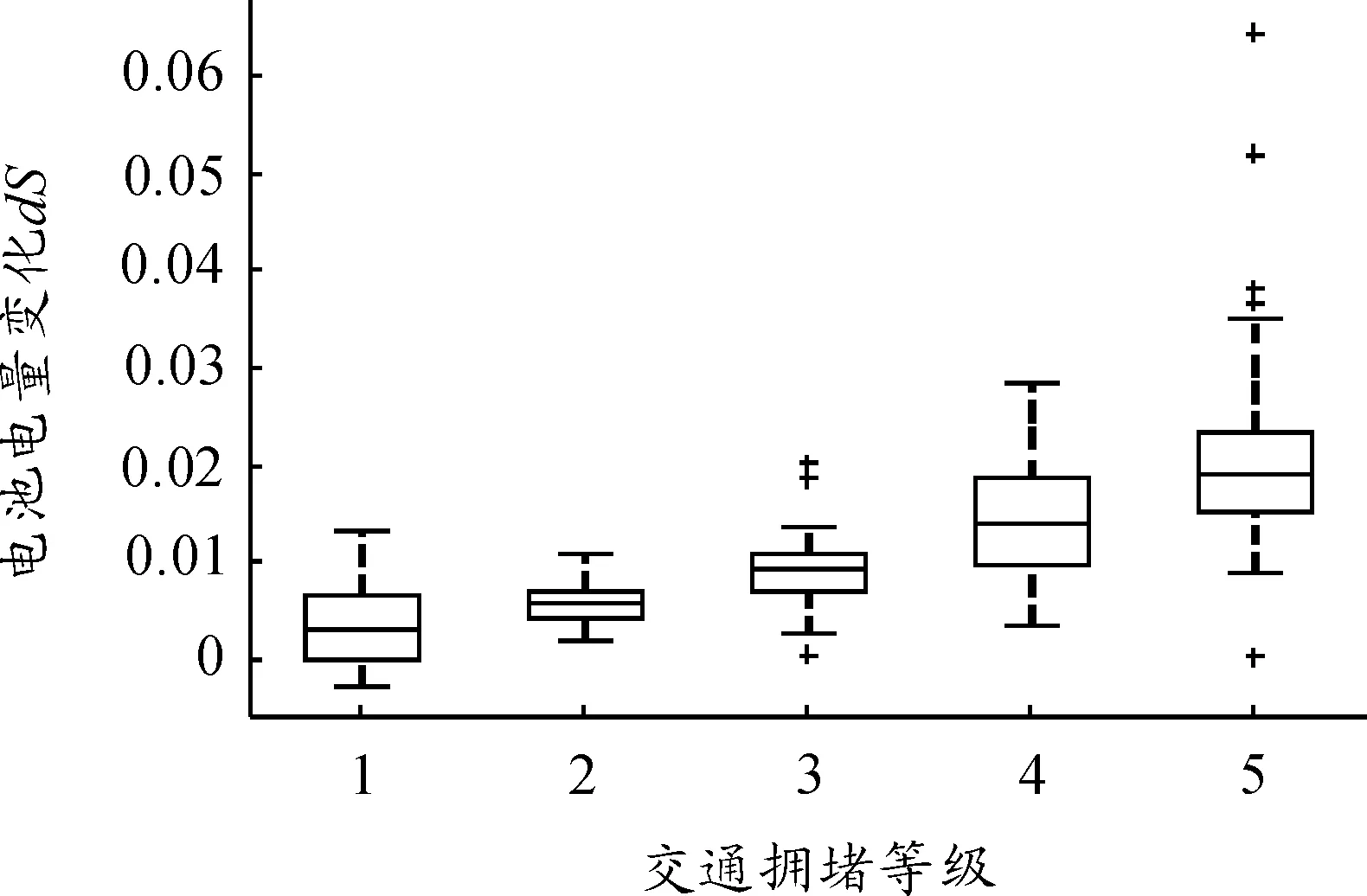
图7 SOC0=0.9时电池电量变化与交通拥堵等级关系

3.1 剩余行程电量分配算法

为了预测剩余行程的车速序列以分配各路段的电池电量，本文设计的复合NARX网络模型如图8所示，其由3个NARX网络模型构成。相对于单NARX网络模型，该复合模型在长时间预测时不会产生振荡。

由于在根据各路段的交通拥堵等级预测车速时并没有在线的前几秒车速可以利用，因此本文随机选取该交通拥堵等级下的历史工况片段的初始5 s车速作为初始数据，然后输入至第1个NARX网络模型中以预测其后的30 s的车速。然后，将此刻已有的35 s车速输入到第2个NARX网络模型中，从而预测此后20 s的车速。第3个NARX网络模型则以此前的55 s的车速为输入，预测当前路段剩余里程的车速序列。

通过从前6组仿真数据中提取的各交通拥堵等级下的工况数据，训练上述复合NARX网络模型，得到了与不同交通拥堵等级相对应的复合车速预测模型。在线应用时则先从ITS中获取各路段的拥堵等级，然后利用对应的车速预测模型预测各路段的车速序列，并组成剩余行程的车速序列，最后利用DP算法计算出电量消耗轨迹，从而获得各路段的电量分配结果。

为了研究通过上述剩余行程电量分配算法分配电池电量的效果，对比了所预测的工况和采集的第7组工况所对应的全局最优SOC轨迹，结果如图9所示，二者的变化趋势几乎一致，但预测工况对应的SOC轨迹存在累积误差，表明仅依据交通拥堵等级可以获得良好的全程电量分配结果。

图8 复合NARX网络模型

虽然通过上述电量分配算法实现了良好的全程电量分配，但当车辆行驶在当前路段时，可进一步利用更多的实时信息，如前车车速、跟车距离、交通灯状态及自车历史车速等，以提高当前路段上车速预测的准确性。

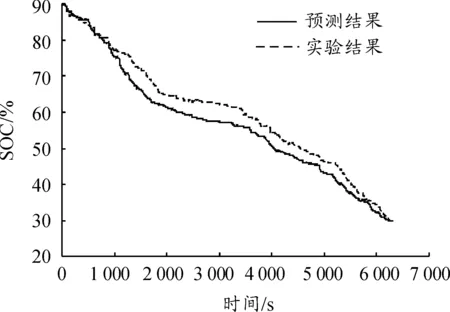
图9 预测工况与实验工况最优SOC变化对比

3.2 当前路段电量消耗轨迹预测算法

针对当前路段上不同阶段的特点，本文设计了3阶段车速预测算法，一方面避免了预测时长有限的问题，另一方面充分结合了不同阶段的特点，算法结构如图10所示。

图10 3阶段区间路段车速预测算法

当车辆行驶在当前路段上时，其自车车速、自车位置、前车车速和前车距离均会影响未来短时间的车速。利用这些信息作为未来20 s车速预测神经网络模型的输入，得到了比只以自车车速为依据的Markov模型更好的车速预测结果，该神经网络模型的预测结果如图11所示。

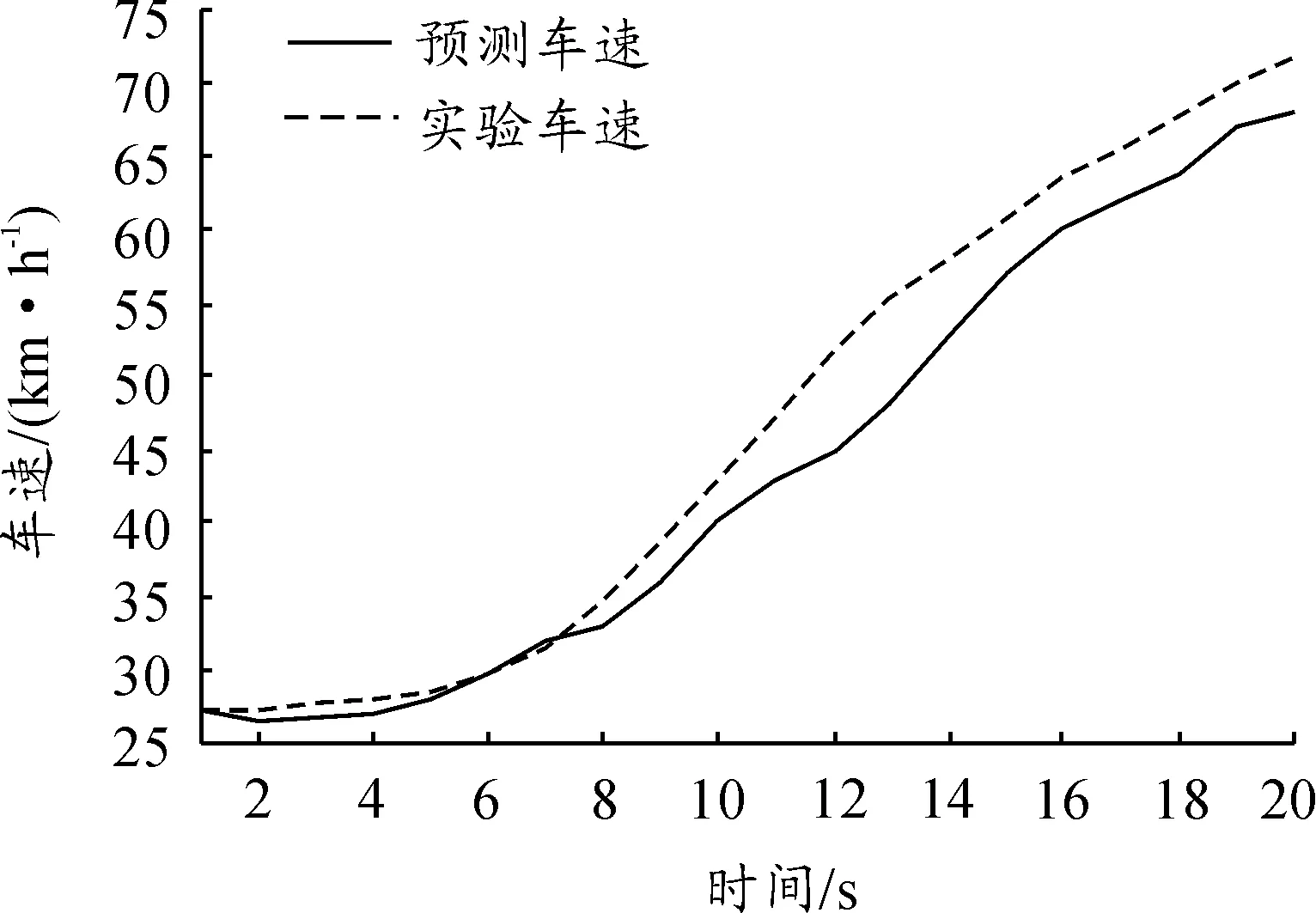
图11 第1阶段神经网络模型预测结果

以第1阶段神经网络模型预测的20 s车速为输入，利用本文3.1节中的复合NARX网络模型作为第2阶段的车速预测模型。图12展示了分阶段的车速预测与不分阶段的车速预测(仅复合NARX模型预测)的结果对比，可以看出：基于上述2个阶段的车速预测模型的预测结果与实验结果相当，同时优于无第1阶段的模型。

第3阶段由于接近路口，因此在第1阶段输入参数的基础上增加了与路口距离及交通灯状态2个输入，建立了神经网络模型。对比采用第1阶段和第3阶段模型进行车速预测的结果，发现新增的2个输入在车辆接近路口时能明显地改善车速预测效果，结果如图13所示。

图12 第2阶段复合NARX网络模型预测结果

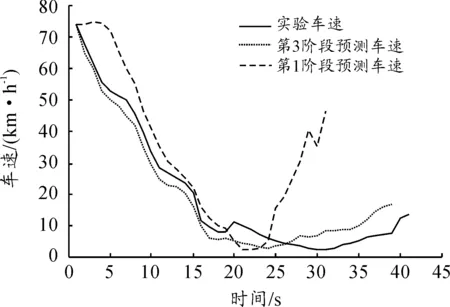
图13 第3阶段神经网络模型预测结果

由于融合了更多实时交通信息和道路信息，上述3阶段区间路段车速预测算法比图8中的复合NARX网络模型在区间路段上预测的车速更加接近实验数据。由于预测出了当前路段的车速序列，且由本文3.1节中的剩余行程电量分配算法可以得到当前路段结束时的SOC，因此可以再次利用DP算法得到当前路段的最优SOC轨迹，并以此作为参考曲线用于设计在线能量管理策略。

4 电量消耗轨迹跟随算法

4.1 算法介绍

在计算最优电量消耗轨迹的过程中，本文未研究DP的运算复杂度，在线应用时可以考虑借助云计算平台完成上述计算任务。由于交通拥堵等级的变化较慢，因此在实施本文3.1节所描述的剩余行程电量分配算法时可每隔2个路段计算1次。本文3.2节中的分3个阶段的当前路段电量消耗轨迹预测需要更高的实时性，因此可以每隔15 s实施一次。

由本文第3节可获得最优电量消耗轨迹，在线能量管理策略则可依据实际SOC与该曲线的偏离情况和整车需求功率的大小决定动力系统的工作模式和功率分配。当实际SOC大于参考的SOC一定值时，可以在满足需求功率的条件下尽量多耗电。当实际SOC小于参考的SOC一定值时，可以在满足需求功率的条件下发电且保证发动机工作在高效区间内。

4.2 算法性能分析

利用线路7的数据验证所设计的电量消耗轨迹跟随算法的性能，以SOC0=0.9为例，对比离线DP得到的最优电量消耗轨迹、预测出的电量消耗轨迹、在线电量消耗轨迹跟随算法的结果及CDCS策略的电量消耗轨迹，如图14所示，表明跟随算法与最优电量消耗轨迹相近。

图14 SOC0=0.9时多种策略SOC轨迹比较

利用线路7的数据，对比不同SOC0下各算法的油耗，计算出DP算法与本文提出的跟随算法相对CDCS策略的节油率，如表2所示。

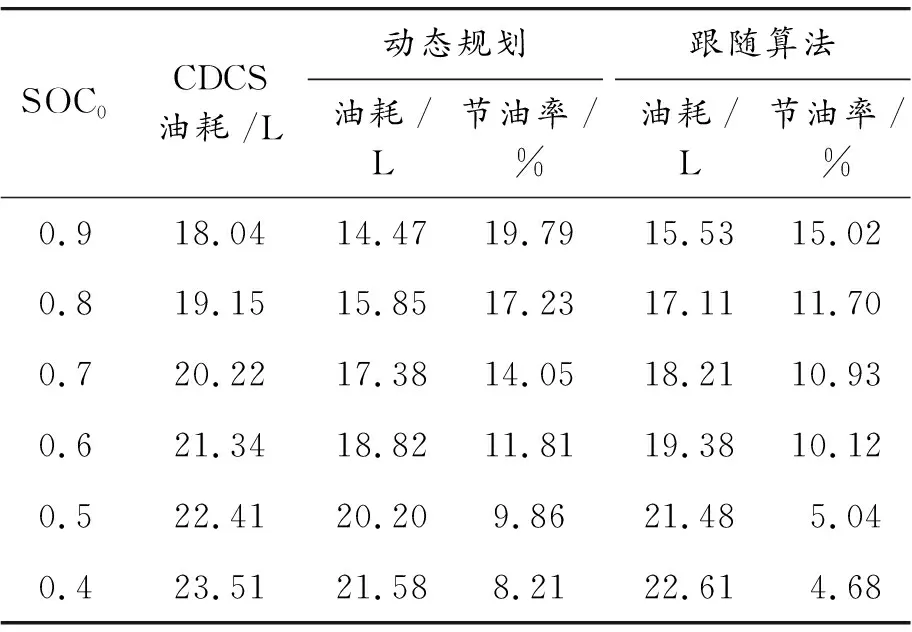
表2 不同算法和SOC0下的油耗计算结果

从表2可以看出：本文所提出的基于ITS的电量消耗轨迹跟随算法相对于CDCS策略能稳定地降低油耗，且与动态规划得到的最优解相近。

5 结论

本文设计了考虑多种交通信息的插电式混合动力汽车电量消耗轨迹预测与跟随算法，即首先利用各路段的道路拥堵等级进行车速预测并获得各路段的电量分配结果，然后在当前路段的尺度上利用更多信息进行车速预测，并结合路段可用电量得到参考SOC轨迹。在线应用时则以实际SOC值与参考SOC值的偏差进行反馈调节，使得车辆的真实SOC轨迹跟随参考轨迹。基于该电量消耗轨迹预测与跟随算法，仿真得出相比于CDCS策略其节油率最多可达15.02%，并接近动态规划算法的全局最优解。