基于benders分解法的生鲜农产品“最后一公里”配送路径优化

常馨玉，庞知非，刘振国，尚晋平

（1.交通运输部科学研究院，北京 100029；2.交通运输部公路科学研究院，北京 100088）

1 引言

随着经济的发展和居民消费水平的提高，我国生鲜农产品的流通量逐年增加，加之电子商务的飞速发展，各类企业纷纷涉足生鲜电子商务。由于生鲜农产品本身的特殊性以及在流通过程中对运输时间有较强的敏感性，要求尽可能的减少运输过程中所消耗的时间，保证生鲜农产品的新鲜程度。我国的冷链干线运输经过几十年的发展，已经能够满足人们对于生鲜农产品消费的需求，而从配送中心到客户手中的“最后一公里”物流配送是电商降低物流成本、提高配送效率、抢夺生鲜配送市场的关键所在，也是全面贯彻落实物流业降本增效的抓手。

2 国内外研究现状

国外最先开始研究生鲜物流配送问题，PedroAmorim[1]等研究食品配送过程中的配送车辆路径优化过程，但并没有将食品的损耗考虑在内；Solomon[2]等将客户点的收货时间窗约束条件加入到生鲜农产品物流配送问题的模型中，满足了生鲜物流配送问题的时效性要求；Miroslaw[3]等提出生鲜农产品在配送过程中需要满足客户的需求、配送服务时间以及产品的新鲜度等条件，将客户点的收货时间窗和配送车辆的控制温度作为约束条件，构建以配送成本最小化为目标的混合整数规划模型；Dabia[4]等提出为了减少配送所需要的时间并降低配送成本，可以在与客户约定的时间段内提供配送服务。国内一些学者也对生鲜农产品的末端配送展开了研究，并取得了相应的成果，杨芳[5]等构建了基于安全和效率的多目标MAS系统模型，提高了生鲜果蔬的流通效率；龚树生，梁怀兰[6]等研究了生鲜食品的冷链物流网络；王红玲[7]等构建了以生鲜农产品在途时间最短、配送成本最小为优化目标的规划问题；石兆[8]等通过建立在时变条件下的仿真模型来求解配送网络的最优路径；杨婷[9]、邵举平[10]等以客户的满意度极大化作为约束条件来优化配送路径。

生鲜农产品的配送问题本质上属于车辆调度（简称VRP问题）问题，是NP-hard问题，因此运用精确算法求解的难度较大，目前对VRP问题的研究大多采用启发性算法，并取得了一定的成果。在求解算法方面，Humberto[11]等运用模拟退火算法对带有时间窗的VRP问题进行求解；Zhang[12]等采用禁忌搜索算法对冷链物流配送路径进行了优化研究；Arbelaitz[13]等建立了带有时间窗的冷链配送路径问题的模型，通过MEAT启发式方法和路线规划启发算法相结合，从而缩小了可行解的搜索范围；Baker（2003）[14]利用遗传算法解决了最基本的VRP问题；Blanton和Wainwright（1993）[15]、Potvin（2002）[16]等利用遗传算法解决了带时间窗的VRP问题。

本文针对生鲜农产品的最后一公里配送问题的特点，引入了生鲜损耗度系数来反映生鲜农产品随时间推移而下降的特点，并建立了在满足客户点收货时间窗的基础上，配送成本最低的混合整数规划模型，并采用精确算法本德斯分解法（benders decomposition）来对该模型进行求解。

2.1 问题描述

本文研究的是城市内生鲜农产品的最后一公里配送问题。问题以配送成本最小化为目标，采用同类型电动三轮车实现生鲜农产品的最后一公里配送。

问题的特点如下：

（1）运输网络包含两类节点：区域配送中心及该配送中心辐射服务范围内若干有配送需求的客户点。其中区域配送中心是配送车辆的始发/终到点。

（2）配送车辆的车型相同，且其额定载货量、实载率、速度、行驶成本等已知。

（3）客户点的货物需求已知且不可拆分，每个客户点的货物需求量不超过一台配送车辆的额定载货量。所有客户点均有收货时间窗限制。在配送周期内配送车辆服务全部客户点，每个客户点每天只能被服务一次。

（4）配送成本主要考虑行驶成本、等待时间惩罚成本和生鲜农产品损耗成本。

2.2 参数及变量

将上述问题定义在有向图G=(V,A)上，V={0,1,...,n}为点集合，其中，0表示区域配送中心，V{0}表示配送网络中等待配送服务的客户点。具体参数及变量含义见表1。

表1 参数及变量

2.3 建立模型

目标函数：

约束条件

目标函数式（1）表示总配送成本的最小化，由三部分组成：第一部分为配送过程的行驶成本；第二部分为配送过程中配送车辆在客户点处等待的惩罚成本；第三部分为配送过程中生鲜农产品生鲜度损耗成本。

约束（2）表示配送车辆进出场站的次数为1；约束（3）表示对于任一客户点来说，只能被一辆配送车辆服务一次；约束（4）表示配送车辆k的进出节点流平衡，且每辆配送车辆对同一个节点服务一次；约束（5）确保了每台配送车辆服务客户点的货物需求总量不超过该配送车辆的实际载货量；约束（6）和（7）表明了配送车辆从区域配送中心出发时间与到达第一个客户点处的到达时间的关系；约束（8）和（9）表明了配送车辆在两个客户点的到达时间之间的关系，约束（10）和（11）表示配送车辆要满足客户点的取货时间窗要求；约束（12）-（14）定义变量 dtk、atki、wtki的取值范围为非负。

3 第一种benders分解策略

benders分解法（简称BD）[17]的基本原理是将模型按照变量类型分解为主问题和子问题，其中主问题包含0-1整数变量，子问题包含连续变量。首先求解主问题获得0-1变量的初始解，并将初始解作为输入来求解对偶子问题，若子问题的对偶问题有界，那么通过求解对偶问题可得到benders最优割，若子问题无界，则得到benders可行割，将得到的割约束添加到主问题中，重建主问题并求解，如此循环迭代，直到求解主问题得到的下界值和求解子问题得到的上界值相等或在一定的偏差范围内，算法停止，得到最优解。

按照经典benders分解法的思路对模型进行分解，分解得到的子问题及重建主问题如下：

3.1 子问题及其对偶问题

主问题包含的约束条件为（2）-（5），固定模型中约束条件（6）-（11）中的整数变量xkij来确定子问题。

目标函数：

约束条件：

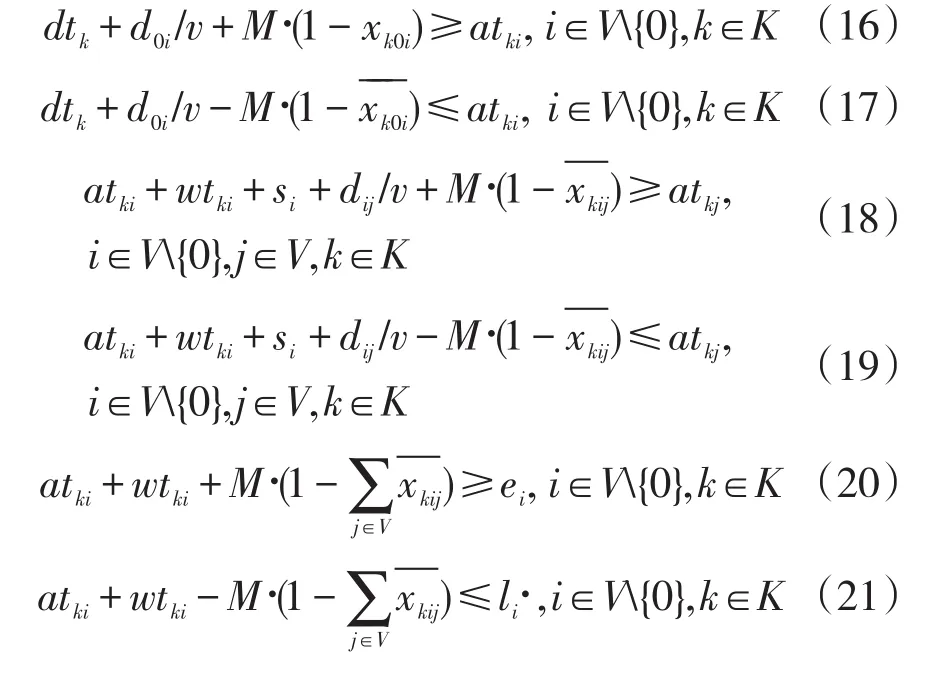
将约束条件转化为原问题的标准形式得：

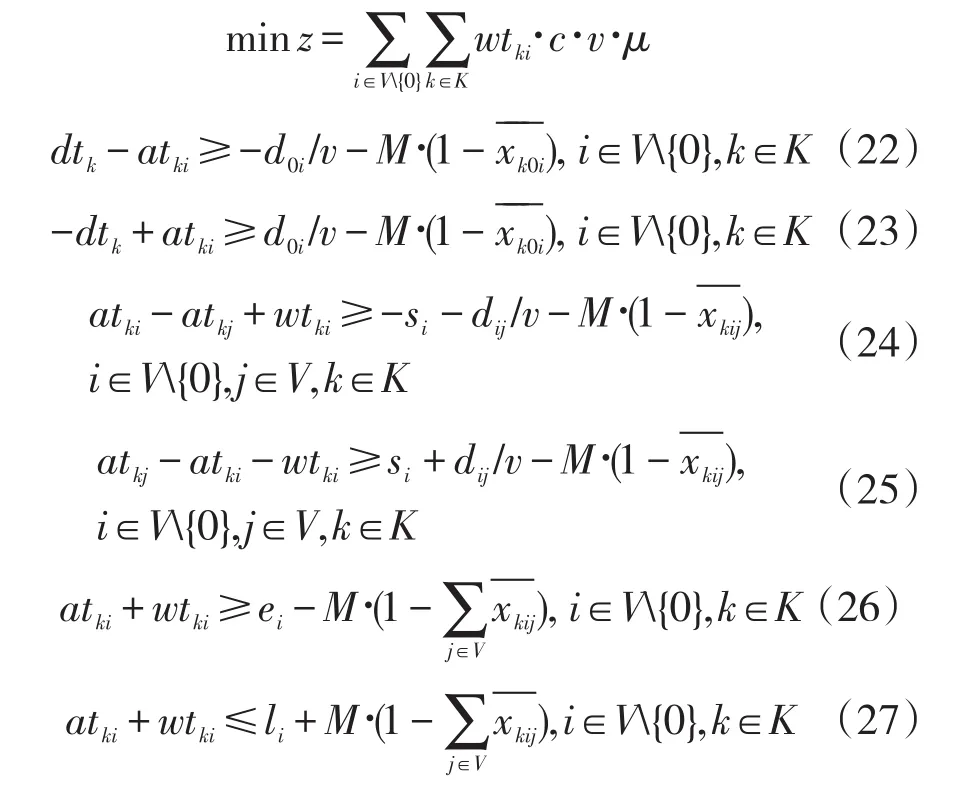
为约束条件（22）-（27）分别设置对偶变量 uki、根据对偶原理得到原问题的对偶问题如下所示：

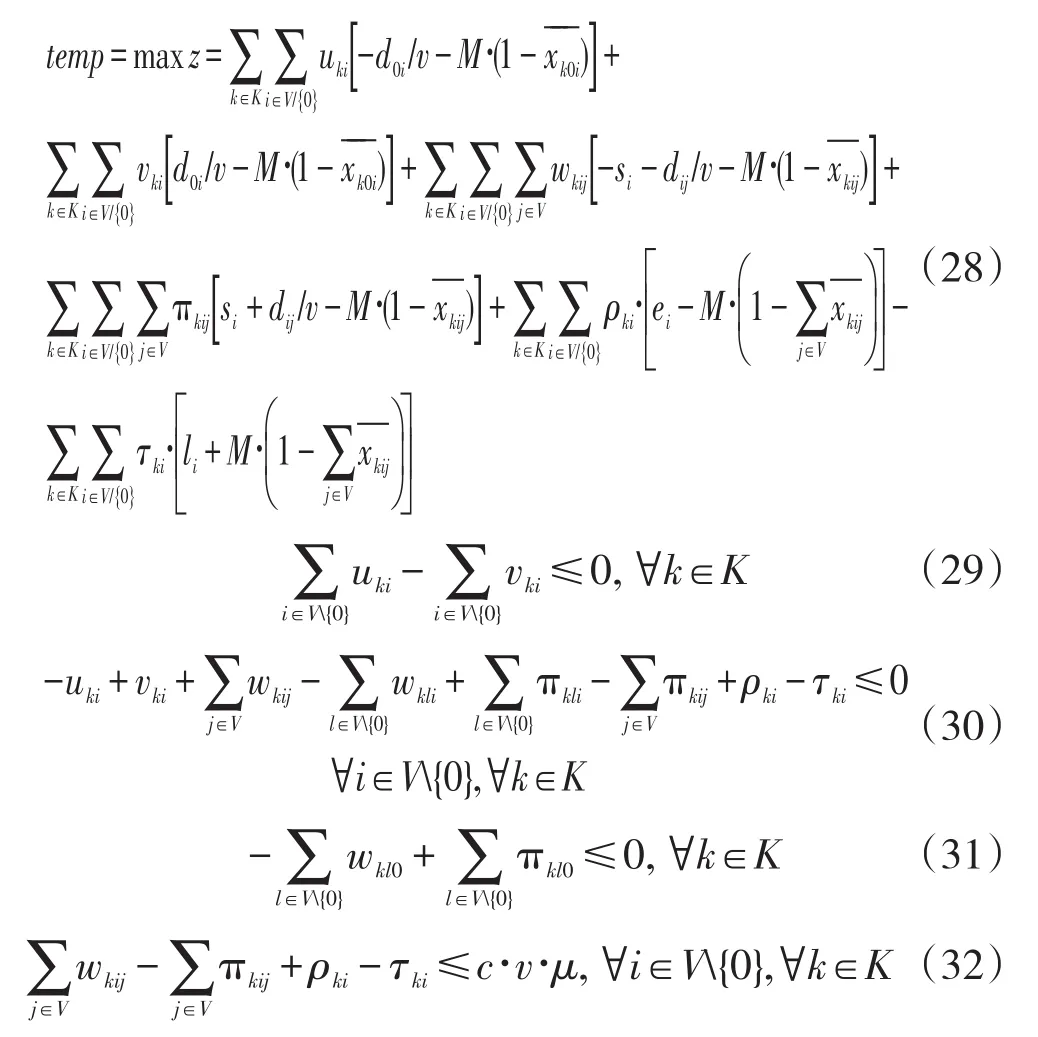
约束（29）是针对变量dtk得到的对偶问题约束条件，约束（30）是针对子问题中的变量atki,∀i∈V{0}的约束条件，而约束（31）为针对原问题中变量atk0的约束，约束（32）是针对变量 wtki,∀i∈V{0}的约束。

3.2 重建主问题

引入自由变量θ，将生成的benders割约束加入到主问题中，生成重建主问题：

4 第二种benders分解策略

在第一种分解策略中，主问题中只包含一个变量，子问题中包含三个变量，这种分解方法可能会导致主问题不够完整，而子问题的规模偏大，因此在第一种分解策略的基础上提出了第二种分解策略，这两种分解策略的区别在于第二种分解策略将连续变量atki、dtk作为主问题中的变量，而子问题中只包含连续变量wtki，这种分解方式可以使得主问题相较于第一种分解策略更加完整，得到的主问题的初始解更合理。

4.1 子问题及其对偶问题

相较于第一种benders分解策略，第二种分解策略中主问题包含的约束条件为（2）-（9），固定模型中约束条件（10）-（11）中 xkij、atki值来确定子问题。

将求解主问题获得的xkij、atki值作为初始值带入到子问题中，得到了原问题对应的子问题，子问题中包含连续变量wtki：

目标函数：

约束条件：

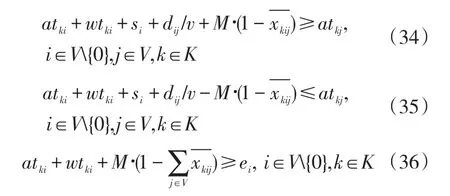
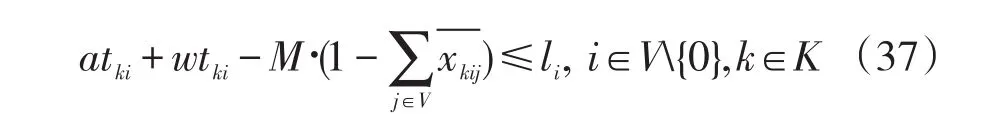
将约束条件转化为标准形式得：

为约束条件（38）～（41）分别设置对偶变量 wkij、根据对偶原理得到原问题的对偶问题如下所示：

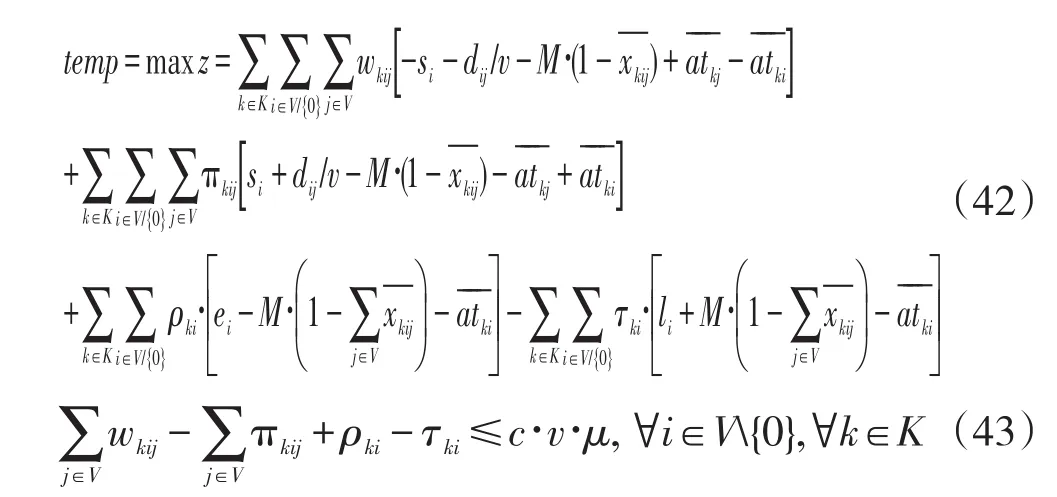
约束（43）针对变量 wtki,∀i∈V{0}。

4.2 重建主问题

引入自由变量θ，将生成的benders割约束加入到主问题中，重建主问题：

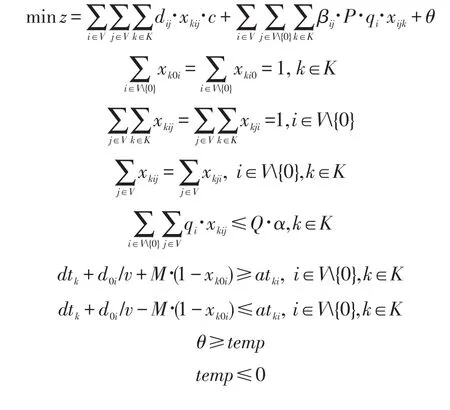
5 算例生成

5.1 方法

为了检验模型的合理性以及算法的有效性，本文结合城市物流配送实际并利用Matlab生成一系列随机算例，算例相应变量见表1。

（1）网络节点坐标以及距离矩阵dij。城市生鲜“最后一公里”配送的运载工具以电动三轮车为主。以1km为单位建立坐标系。在配送过程中，考虑到电动三轮车一次充电后的续航里程以及一辆车配送的范围，可设定其最大行驶距离Dmax=15km。由此可以确定客户点均应位于以(7.5,7.5)为圆心、7.5km为半径的圆内。在该圆内随机生成若干个客户点坐标，利用各节点的坐标空间分布来计算两节点之间的欧氏距离dij。

（2）客户点的订单量qi。考虑到电动三轮车的最大载重量为600kg左右，以一天送50单货物可知，货物重量范围为（1kg,12kg），随机生成该范围内客户点的订单量。

（3）客户点取货时间窗[ ]ei,li。在本文研究中，生鲜农产品的配送需要考虑到时效问题，在配送过程中需要满足客户点取货时间窗的要求，因此本文借鉴Solomn[2]（1987）中的方法生成客户点的时间窗，假设配送服务从时间t开始。

假设客户点i为区域配送中心辐射服务区域内的客户点，配送车辆在客户点i处的服务时间为si；t1=ei+dij/v为配送卡车在i点无需等待时的时间窗下限的最大值；t2=li-dij/v-si为配送卡车刚好能够完成配送活动的时间窗上限值。随机生成[t1,t2]范围内的数t3作为时间窗中心，并且利用正态随机分布生成时间窗半径t4，则客户点i处的时间窗下限为ei=max(t,t3-t4)，时间窗上限为li=min(t2,t3+t4)。

（4）客户点处的派件服务时间。按照实际经验取5min-20min内的随机数即可。

5.2 参数设置

随机算例的参数设置见表2。

表2 随机算例的参数设置

5.3 算例计算结果

本文运用CPLEX 12.4软件结合VS 2010软件编程实现两种benders分解法，并对随机算例求解，计算结果见表3，其中第一列表示算例编号，算例编号“mn”表示包含m个客户点的第n个算例，如算例“5-1”表示包含5个客户点的第1个算例；第三列表示该模型的目标函数，即车辆的配送成本；第四、五列表示所需要的配送车数量以及相应的配送路径；第六列表示不同分解方式所需要的计算时间；第七列表示benders分解过程中上界值和下界值之间的偏差。

表3 算例计算结果

从算例计算结果来看，两种分解策略得到的目标函数值和配送车辆的路径是一致的，表明这两种分解策略均能在一定时间内给出算例的最优路径，同时也表明模型的准确性及算法的有效性；从计算时间看，70%算例的第二种分解策略的计算时间优于第一种分解策略；从算法计算的收敛情况看，70%的算例第二种分解策略的收敛效果优于第一种分解策略。结合这两方面来看，第二种分解策略的计算效果要优于第一种分解法。从benders算法的基本原理来看，本文所讨论的问题本质上为路径优化问题，每次迭代过程中模型的完整度对解的质量有很大的影响，第二种分解策略在每次迭代的过程中，主问题所包含的变量和约束条件比第一种分解策略更多，主问题的完整度相较于第一种分解策略更高，主问题越完整，每次求解主问题获得的初始解就会更加合理，那么初始解带入子问题后求解子问题得到的割约束的约束力会更强，在求解重建主问题时算法会收敛的更快，体现在算例计算结果中，70%的算例运用第二种分解策略的求解速度更快。

6 结语

本文研究了时间窗约束下的生鲜农产品最后一公里配送问题，建立了车辆调度的混合整数规划模型，利用两种不同的benders分解策略对随机生成的算例精确求解，对生成的配送路径进行了优化实证，验证了模型的准确性和算法的有效性，得到了不同客户点规模下的最优配送方案，计算结果证明第二种benders分解策略能够在较短的时间内给出随机算例的最优路径方案，为城市配送车辆调度问题的求解提供了一种新的方法。