基于云计算的道路行程时间预测方法

（武汉理工大学，湖北 武汉 430070）

1 前言

中国正处于从工业化到城市化的转变过程中，交通网络对于城市的建设具有重要意义。然而，由于中国城市人口的急剧增加，中国人均汽车保有量的上升，城市交通网络的负荷过大，由此导致了城市内部交通拥堵、交通事故频发等问题。为了解决这一问题，众多专家学者进行研究，并提出一种从交通管理入手的解决方案，即智能交通系统。

智能交通系统[1]（Intelligent Transportation System）简称ITS，它的主要方法是通过技术手段，把道路交通、人、车紧密结合起来，综合解决道路交通中所出现的问题。然而，随着城市内交通量的增大，智能交通系统产生的数据也在急剧增大，这些数据对于智能交通系统的后台是巨大的挑战，并且，在现有的智能交通系统的构建过程中，软硬件都是和系统紧密绑在一起的，这就造成了各个物理子系统的分离，各个系统之间容易产生数据孤岛现象，很难对数据实现综合分析。而云计算具有储存数据量大、计算速度快的特点，基于此，本文提出一种基于云计算的道路行程时间预测系统。

该系统用环形感应线圈检测器、微波检测器、超声波检测器等车辆信息监测器获得道路交通信息并将信息通过无线网络传输到云计算平台，云计算平台对传输过来的道路交通信息进行处理并建立历史数据库，利用卡尔曼滤波算法和历史数据库对道路的行程时间实现多步预测，利用云计算平台可以将预测的结果发送到用户的移动设备上，能够让用户避开交通拥堵的路段，节约用户时间。

2 基于云计算的道路行程时间预测系统框架研究

2.1 云计算简介

对于云计算，目前还没有统一的定义，概括而言[2]，云计算是一种对IT资源的使用模式，对共享的可配置资源，提供普适的、方便的、按需的网络访问，使用时不需要很大的管理代价。云计算具有高可靠性、高可拓展性、按需服务和廉价等特点，学术界对云计算的服务方式进行了总结，目前一致认为云计算能为用户提供三种服务方式，包括基础设施即服务（IaaS）、平台即服务（PaaS）和软件即服务（SaaS），其中基础设施即服务主要能为用户提供相应的计算和储存能力，平台即服务能为用户提供应用程序开发、数据库、应用服务器、试验、托管及应用服务，软件即服务能为用户提供定制的软件使用服务。其中，平台即服务是云计算服务模式中最为关键的一层，在整个云计算体系中起着支撑的作用。

2.2 基于云计算的道路行程时间预测系统框架

为了能对道路的行程时间进行准确的预测[3]，需要采集大量的道路信息，为了能减少信息孤岛现象的出现，同时也能够对交通中产生的大数据信息进行有效的储存和计算，提出基于云计算的道路行程时间预测系统，系统的框架如图1所示，系统的框架主要包含四层。

第一层为基础设施层。该层主要包括视频检测器、磁感应线圈检测器和超声波检测器等自动交通数据采集设备采集道路交通中的信息，采集的道路交通信息通过4G/5G网络的方式传输到云计算平台的基础设施层即服务层。

第二层为云计算的IaaS平台层，该层主要是提供虚拟资源，比如海量的计算资源和存储资源，接受基础设施层通过网络传输过来的数据。

图1 基于云计算的道路行程时间预测系统框架

第三层为云计算的PaaS平台层，该层能够对数据进行预处理，并根据预处理之后的数据建立模型，并根据模型实现对道路行程时间的预测。

第四层为用户层，在云计算平台完成对道路行程时间的预测后，可以通过无线网络将数据传送给用户，帮助用户做好相应的决策，用户有意见也可以通过网络反馈给云计算平台。交管部门利用预测信息做出交通诱导，降低城市道路的交通拥堵。

3 基于云计算的道路行程时间预测模型研究

3.1 道路行程时间的预测模型

现有的对道路行程时间的模型根据对数据要求的不同可以分为以下三个种类：第一类是统计类的方法，该方法侧重于对历史数据进行处理，并从历史数据中查找规律，并基于这些规律对未来的道路行程时间进行预测，以历史趋势法作为代表；第二类是使用技术类的方法，对当前交通数据进行分析，并预测下面时刻的道路行程时间，比如神经网络算法、卡尔曼滤波算法等；第三类是仿真类算法，主要用计算机对道路交通状况进行模拟，从而预测出道路的行程时间，比如VISSIM系统。考虑到在道路行程时间预测时计算的实时性、预测精度、复杂性以及在线调整等因素，卡尔曼滤波算法比较合适。因此，选取卡尔曼滤波算法对道路的行程时间进行预测。

卡尔曼滤波算法是由Kalman和Bucy在1960年提出的，它是一种时域上的状态空间方法，自被提出以来，已经被应用到很多领域，比如社会经济、航空航天和工业工程等领域，中国学者杨兆升[4]在1999年曾用卡尔曼滤波模型对行程时间进行预测。

3.2 卡尔曼算法的单步预测模型

卡尔曼滤波算法可以用下面的式子进行表示，先引入一个离散控制过程的系统，该系统可用下面一个线性随机微分方程来描述。

其中，TK表示K时刻道路的行程时间，uK-1表示K-1时刻对道路行程时间的控制量，A和B表示系统参数，对于多模型系统而言，它们可以表示为矩阵。yK表示K时刻的测量值，H表示测量系统的参数，对于多测量系统而言，H可以表示为矩阵，qK-1和rK分别表示过程和测量的噪声，又被假设为高斯白噪声，假设它们的数值不随时间的变化而变化，那么卡尔曼算法的5个更新方程如下所示：

在上面的式子中，GK表示卡尔曼增益,PK表示系统的误差协方差矩阵，TK-表示预测的K时刻的道路行程时间，PK-表示预测的过程中产生的误差协方差矩阵，式（3）表示基于现在的状况对未来的状况进行预测，式（4）表示计算本次预测时所产生的误差协方差矩阵，式（5）表示计算卡尔曼增益，式（6）表示结合观测到的数据对本次预测进行修正，式（7）表示修正误差协方差矩阵，以为下一步预测准备。上述算法可以使用Matlab语言进行编程并实现计算。上述的卡尔曼滤波算法为单步预测，预测的时长为5-15min左右，若想对更远的时间进行预测，需要进行多步预测。

3.3 卡尔曼算法的多步预测模型

在上述的单步的卡尔曼滤波算法预测道路行程时间中，需要实时的数据进行计算，比如需要实时的对预测模型中的卡尔曼增益进行不断的修正，以使得系统的误差协方差矩阵达到最小，然而实时数据的最佳获取时间都在15min以内，因此限制了单步的卡尔曼滤波算法预测的时间长度。将结合历史上同类型日子的道路行驶时间去实现多步预测[5]。

首先在云计算平台上建立交通信息历史数据库，将每天的道路交通信息都储存在历史数据库中，当需要对道路行程时间进行预测时，从交通信息历史库中选取与当前交通状况比较相似的历史日子，从中选取道路行程时间作为参考，完成对道路行程时间的预测。在评价交通状况是否相似时，见式（8），当前时刻以前的三个时刻的道路行程时间TK-1,TK-2,TK-3与历史数据库中相同时刻之前的三个时刻的道路行程时间TK-1P,TK-2P,Tk-3P的相对误差之和为ZP，当误差之和ZP最小时，则选择出了与当前日子交通状况最相似的历史日子。

在最相似的历史日子中，选取当前时刻以及未来五个时刻的道路行程时间，将这6个数据当作测量值 yK代入到式（1）-（6）进行迭代运算，就能够完成多步的预测，在选取数据时，一般选取周期为5-15min，当周期过长，会导致预测的准确度降低，当周期过短，会导致预测的时间太短，不能够完成道路行程时间的长时间的预测，最后参考以往的研究，选取10min为测量周期，经过6步预测之后，预测的道路行程时间可以提升至60min。

4 基于云计算的道路行程时间预测的模拟仿真

为了对模型进行验证，采集了位于武汉市洪山区珞狮路的道路行程时间的数据，珞狮路全长3.3km[6]，是武汉市洪山区的一条双向主干道，北起八一路，南至南湖大道，由于道路下面修建地铁，珞狮路最近半年内都是武汉市最为拥堵的十条路段之一，早高峰一般出现在从南向北的道路，出现时间为7∶30-8∶30，晚高峰出现在从北向南的路段，出现时间为5∶30-6∶30，早高峰一般出现在工作日，其中周一的早高峰最为拥堵，晚高峰一般出现在周五，周六周日比较相似，但跟工作日的状况明显不同，其中，天气状况对于道路交通有一定的影响。本文主要对早高峰的情况进行模拟仿真。

在建立早高峰的历史数据库时，需要分为六个种类的数据，见表1。当需要调用数据时，就能够更加快速地从历史库中寻找合适的参数对道路的行程时间进行预测。

表1 历史数据库中的存储种类

通过视频检测器采集车牌的信息并利用软件进行自动识别[7]或通过人实际观察的方式采集道路信息，从而能够观测出道路的行程时间，采用10min/次的采集频率对汽车信息进行采集，将采集的信息传送到历史数据库中并分类储存，利用卡尔曼多步预测能够实现道路行程时间的预测，主要对珞狮路两周的道路行程时间进行预测，预测结果和实际值如图2所示。

观察图2可以发现，通过卡尔曼滤波多步预测可以对珞狮路的道路行程时间进行预测，预测的结果与实际的观察值大都是拟合的，道路行程时间的预测值和实际值的变化趋势是趋同的。由图3可知，预测的结果的大部分的百分比的相对误差[8]都在10%以下，其中有一个误差为12%，也在可以接受的范围内，因此可以验证这个算法对道路行程时间的预测是可行的。

5 结论

图2 实际的道路行程时间和预测的道路行程

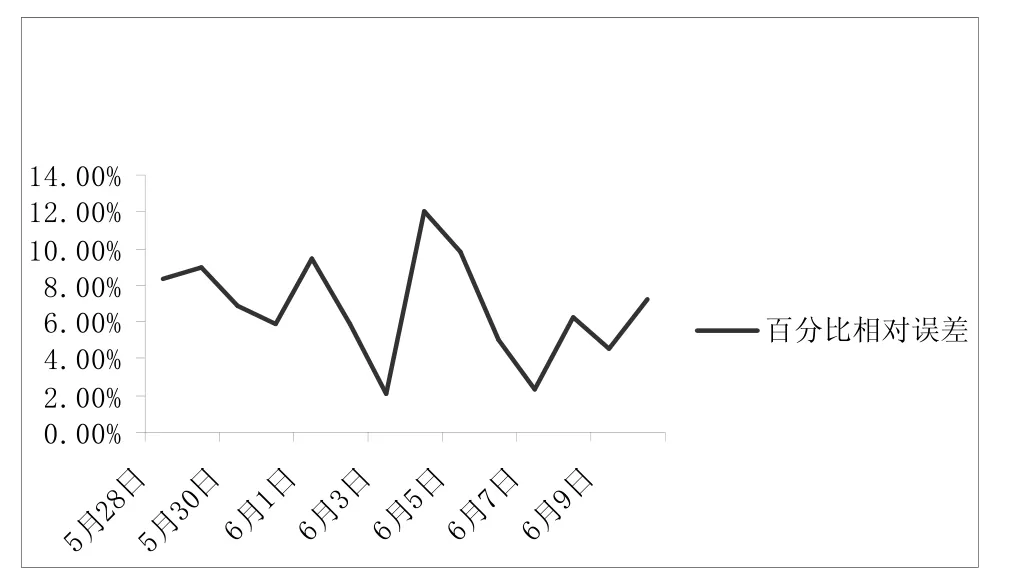
图3 预测的百分比相对误差

由于中国城市人口的急剧增加，中国人均汽车保有量上升，城市交通网络的负荷过大，由此导致了城市内部交通拥堵、交通事故频发等问题，本文对基于云计算的道路行程时间的预测进行了研究，通过传感器采集道路交通信息，通过无线网络将信息传送到云计算平台，通过云计算平台对信息进行分析，利用卡尔曼滤波算法完成道路行程时间的预测，提出相应的算法，并利用算法对道路的行程时间预测进行了仿真，验证了其可行性。利用预测结果可以对道路交通进行实时诱导，对于降低城市交通拥堵和交通事故发生的次数具有重要意义。