基于ARIMA—GARCH模型对股票数据处理过程的探讨和研究

于雅凝 过榴晓

摘 要 基于2016-2017年贵州茅臺股票收盘价数据，应用时间序列分析理论中长期趋势和随机波动之间存在复杂的交互影响关系建立ARIMA-GARCH模型进行分析，首先，对多组数据进行拟合比较，其中ARIMA（2，1，6）模型经检验显著有效。针对波动信息的提取首先是考察ARIMA（2，1，6）模型的残差平方序列的异方差特征，经LM检验和Q检验显示残差序列显著方差非齐，且具有长期相关性。构造GARCH（0，2）模型，并根据该模型的拟合并预测未来股票价格，结果表明该模型效果拟合良好，在短期时间内可以对投资可以起到一定的指导作用。

关键词 时间序列分析 模型预测 ARMA-GARCH模型 股票价格

中图分类号：F831.5 文献标识码：A DOI：10.16400/j.cnki.kjdkx.2018.06.018

Abstract Based on the closing price data of Kweichow Moutai from 2016 to 2017， an ARIMA-GARCH model was established based on the analysis of the complex interplay between medium and long-term trends in time series analysis theory and stochastic volatility. Firstly， multiple sets of data were compared and compared. Among them， the ARIMA （2，1，6） model is significantly effective. The extraction of the fluctuation information is firstly to investigate the heteroscedasticity features of the residual squared sequence of the ARIMA （2，1，6） model. The LM test and the Q test show that the residual sequence has a significant variance， and has a long-term correlation. The GARCH （0，2） model is constructed， and the future stock price is predicted and fitted according to the model. The results show that the model is well-fitted and can play a role in guiding the investment in a short period of time.

Keywords time series analysis； model prediction； ARMA-GARCH model； stock price

0 引言

随着人们生活水平的提高，对高档白酒的消费将不断增加。茅台凭借其“国酒”的地位，销量很高，并且几乎一直处于供不应求的状态。近一段时间内，茅台的股价一直走高，创下了中国股市的很多记录，在中国股市继15年后的低迷状态下，股价仍稳定发展，但是近期增长过快，引发人们注意，几个月之间股价蹿升至600元/股以上，引发了市场的热议。为了防股票价格快速上涨或下跌带来的不利影响，监测股票波动风险具有重要的意义。

在金融市场，一般采用波动率来衡量股票价格的不确定性。波动率是单位时间内价格的变异率。在计算波动率时，首先对它的波动过程建立适当的数学模型，之后再根据回归模型的条件方差进行换算。如果指数序列不存在波动群聚问题，自回归单整移动平均（ARIMA，以下使用简称ARIMA）模型就是非常合适的解释模型。集群效应（以下用简称ARCH代替）多应用于分析股市行情中。我们将使用ARIMA模型来分析并估计贵州茅台股票的走势及发展。

一直以来，不断有学者对股票价格进行分析和预测，希望摸索出这些数值背后的规律，以规避再一次的股票市场的危机。目前公认的有ARIMA模型及该模型的衍生模型（GARCH模型）适合研究预测股票数据。孟坤等进行了基于ARMA模型预测股票价格的实证分析，[1]得到很好的拟合效果；李丽等使用了ARIMA模型对特定的股票数据进行短期预测；[2][3]刘洪玉对房地产价格的拟合与预测的效果比较ARIMA模型和GARCH模型的差异，[4]房地产和股票的数据特点在一定程度上有相似之处，可以参考该文章中的方法。

本文选取的贵州茅台（600519）从2016年11月10日至017年11月10日的股票收盘价，这段期间内的股票价格走势较稳定，期间未出现重大财务事件，干扰因素较少，有一定参考价值。

1 模型简介

1.1 ARMA（p，q）模型与GARCH模型介绍[5]

自回归滑动平均模型（ARMA（p，q） 模型，Auto-Regressive and Moving Average Model）是研究时间序列的重要方法，由自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。

模型的形式为：

GARCH模型考虑了异方差函数的p阶自相关性而形成的，它可以有效的拟合长期记忆性的异方差函数，ARCH模型是GARCH模型的一个特例（当p=0的GARCH模型）。

结构如下：

1.2 ARCH效应[5]

在宏观经济领域和金融领域，经常可以看到具有如下特征的时间序列：它们在消除了确定性非平稳因素的影响后，残差序列的波动在大部分时段是平稳的，但会在某些时段波动持续偏大，在某些时段波动持续偏小，呈现出集群效应。

2 股票收盘价的模型建立与预测

本文选取了贵州茅台（600519）在2016年11月10日至2017年11月10日的股票收盘价，之后的十个交易日的数据作为测试数据，该公司属于酒水行业的龙头企业，且近些时间无重大事情股权更改事件发生。

2.1 数据预处理

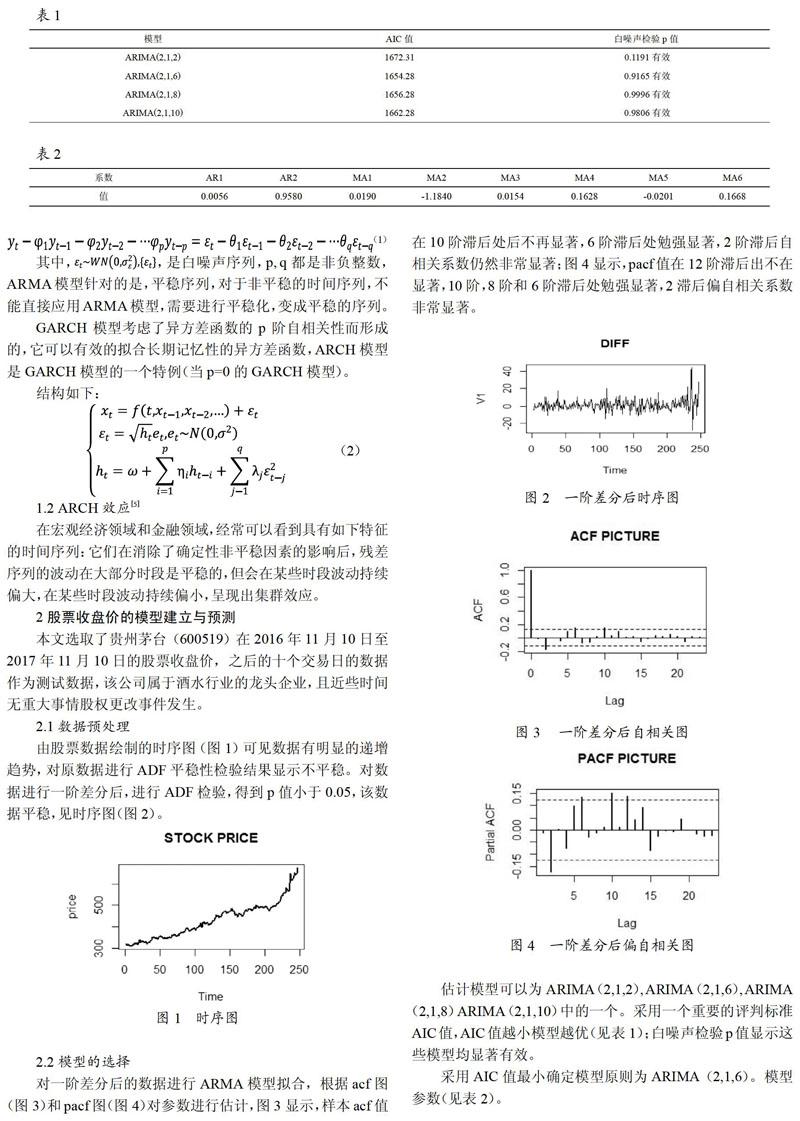
由股票数据绘制的时序图（图1）可见数据有明显的递增趋势，对原数据进行ADF平稳性检验结果显示不平稳。对数据进行一阶差分后，进行ADF检验，得到p值小于0.05，该数据平稳，见时序图（图2）。

2.2 模型的选择

对一阶差分后的数据进行ARMA模型拟合，根据acf图（图3）和pacf图（图4）对参数进行估计，图3显示，样本acf值在10阶滞后处后不再显著，6阶滞后处勉强显著，2阶滞后自相关系数仍然非常显著；图4显示，pacf值在12阶滞后出不在显著，10阶，8阶和6阶滞后处勉强显著，2滞后偏自相关系数非常显著。

估计模型可以为ARIMA（2，1，2），ARIMA（2，1，6），ARIMA（2，1，8）ARIMA（2，1，10）中的一个。采用一个重要的评判标准AIC值，AIC值越小模型越优（见表1）；白噪声检验p值显示这些模型均显著有效。

采用AIC值最小确定模型原则为ARIMA（2，1，6）。模型参数（见表2）。

2.3 模型的检验

利用R软件对模型进行6阶纯随机检验，据纯随机性结果显示，假设序列具有纯随机性，检验在各阶延迟下Ljung检验统计量的p值均大于0.05，所以假设成立，说明：数据的残差序列的各项之间没有任何相关关系，在进行完全无序的随机波动。该模型显著成立且较优。

2.4 异方差性检验

观察数据的一阶差分后的残差平方图（图5），数据在第200组之后有较大的波动聚集在一起，是明显的集群效应，[6]对拟合ARIMA（2，1，6）模型的残差数据根据Box-Ljung统计量[7]进行6阶条件异方差检验（Portmanteau Q 检验），结果如表3：

检验结果显示P值均接近零值，拒绝原假设，所以残差序列方差非齐，具有自相关性，所以具有明显的集群效应。

进行6阶拉格朗日乘子检验（LM检验）的结果和Q检验结论相同。即残差平方序列具有自相关性，可以用GARCH模型拟合。LM检验和Q检验得到的结果一样，这说明1阶至6阶模型均显著成立，残差平方序列具有长期相关。

2.5 异方差模型拟合

对ARIMA模型的残差序列进行异方差性拟合，得到GARCH（0，2）参数显著性最优，模型拟合效果最好。对GARCH（0，2）模型进行白噪声检验来检验模型，[8]可以观察到p值均大于0.05（见表4），则残差为白噪声。

拟合得到的模型为：

利用R软件对下周五个交易日的股票收盘价格进行预测（预测图如图6）并将模型预测值和实际值进行比较，并计算其精度，这里的精度是使用的相对精度（见表5）。

从表5的预测值和真实值的比较可以看出，模型预测效果较好，精度均在95%以上，但是从第四次开始精度降低到96.121%，说明该模型在短期预测内效果好，时间长了，随着市场的波动，不确定因素增加，若不及时调整模型误差会增大。所以，对预测结果进行分析我们可得出以下结论：

（1）ARIMA-GARCH模型进行股票数据模拟是可行的，通过预测图可证明预测效果良好，这个模型包含了股票数据的大部分信息，根据预测，股价将渐渐增长，由每股680.3361将涨到693.1059，目前值得买入；而实际值确实在波动中上涨，最高有719.11元/股，如果13日买进将可以获益。

（2）时间序列分析是根据历史数据从中挖掘有效信息并设计拟合模型，从而对未来进行预测，美中不足的是，可以影响股票价格预测值的只有随机因素。如果该公司发生些事情，或者国际或国内市场大环境震荡，设计模型并不能将这些影响股价的因素考虑进去，在数据选择时特意选了无重大数据影响的股票数据。但该模型不能预测长期结果，只能进行短期预测，以防市场波动和各种不确定因素影响股票价格不正常走向，预测出现偏差。

3 结论

股票价格的预测富有挑战性，使用多种模型去分析，通过尝试对股票数据进行统计，将数据与模型进行拟合，从而进行对未来价格的预测。文中使用的ARIMA-GARCH模型较好地解决了非平稳时间序列的建模问题，并且对数据进行短期预测取得了很好的效果，说明该模型是可行的。虽然本文是使用的静态模型，但是从理论上是可以进行动态预测，让模型更加灵活。

本文针对2016年11月10日至2017年11月10日的茅台股票收盘价进行建模分析，当样本数据改变时，模型参数也会随之改变，并且对股票价格只能进行短期预测，说明该模型还是很敏感的。在选取数据时要选择期间无重大事故发生或政治因素等引起波动的的数据，这样用ARIMA-GARCH模型拟合的效果更好。

参考文献

[1] 孟坤，李丽.基于ARMA模型预测股票价格的实证分析[J].河北北方学院学报，2016.32（5）.

[2] 馬艳娜.上证指数的预测分析——基于ARIMA模型[J].经贸实践，2017（3）.

[3] 吴玉霞.基于ARIMA模型的短期股票价格预测[J].统计与决策，2016.23：21.

[4] 刘洪玉.基于GARCH与Markov转换模型度量房价波动风险刘洪玉[J].清华大学学报，2012.52（2）.

[5] 王燕.时间序列分析——基于R[M].北京：中国人民大学出版社，2015.

[6] 杨琦.基于ARMA-GARCH模型的股票价格分析与预测[J].数学的实践与认知，2016.3：46-6.

[7] 钟骐.基于ARMA-GARCH模型的股票价格分析及预测[J].财政与金融，2017（1）.

[8] 史代敏.应用时间序列分析[M].北京：高等教育出版社，2011.