一种减小相控阵天线球面近场测量截断误差的方法

于丁 张虎勇 陈佩玉 杨林 傅德民

(西安电子科技大学 天线与微波技术重点实验室,西安 710071)

引 言

根据球面近场天线测量的模式展开理论,天线在无源区域的辐射场可以表示为球面波模式的加权和[1]. 无论是在天线的近场辐射区还是远场辐射区,球面波模式的系数不会发生改变,因此球面波模式系数的求解就成了球面近场测量的核心问题,它是近场和远场之间的一座桥梁. 通常情况下,球面波模式系数是利用各模式之间的正交性,在包围待测天线的采样球面上进行积分来获得. 理论上,如果要得到高精度的计算结果,需要知道整个包围待测天线采样面上的完整数据[2]. 在实际测量中,采样面上的部分区域的近场数据往往不能获得,在近远场变换时,一般将未采样区域的近场置为零. 因此,在扫描面边界就会形成突然的不连续性,这将会引入截断误差. 尤其对于相控阵天线,在波束扫描情况下,当最大辐射方向和扫描面边界相距较近时,往往会引起较大的截断误差.

关于这种截断误差减小的方法在一些文献中有提到[3],例如通过建立一个线性系统的匹配技术对不完整的测量数据来预估球面波模式系数可以减小截断误差[4],通过这种方法也衍生出了许多近场数据的重构技术. 目前减小球面近场测量中的截断误差主要有两种方法:一种是基于模式展开和模式滤波的迭代算法[5-6],利用天线辐射场球面波模式个数是严格由包围待测天线最小球的半径决定的,文献[7]在高整合车载天线测量时用到了这种方法. 另一种方法是基于等效电流(equivalent current, EQC)展开的[8],这种方法把EQC看作最小能量算子,在采样区域和截断区域之间形成一个平滑的过度. 还有将模式滤波方法用在减小平面近场测量中的环境误差[9],这种方法是将平面近场测量求得的方向图经过坐标平移后用球面波模式展开后再进行模式滤波,和球面近场测量的模式滤波本质上是一样的. 本文提出一种通过余弦窗函数对近场数据加权来减小截断误差的方法,根据采样内插原理对近场数据进行加权,使近场数据在采样区域和未采样区域的边界处平滑过渡,从而使截断误差减小.

1 基于模式展开的球面近远场变换

基于模式展开的球面近远场变换的基本思路是天线在无源区域的辐射场用球面波模式的加权和来表示,无论是近场还是无穷远处球面波模式的系数不变,因此在近场区域求得球面波模式系数后通过对特殊函数的大宗量近似就可以求得远区场的性质[1].

设一个线极化探头在包围待测天线近场区域的球面上分别在θ方向和φ方向进行数据采集,在理想情况下探头的输出等于或正比于辐射场电场的强度,则在该球面上辐射场电场的切向场可表示为

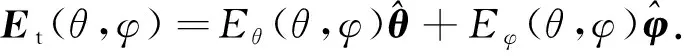
(1)

由于扫描面处于无源区域,因此探头采集的场还可表示为

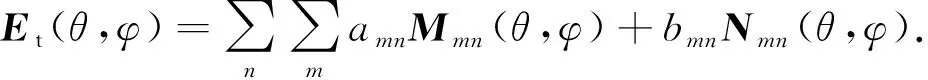
(2)

式中,M和N是标量亥姆霍兹方程的解生成的矢量函数,且满足矢量亥姆霍兹方程,它们的表达式为

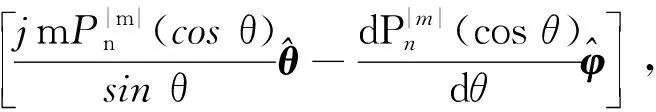
(3)

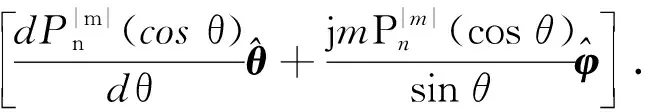
(4)

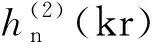
(5)

球面波模式系数amn和bmn可以利用球面波模式的正交性分别乘其共轭在扫描面上积分求得:

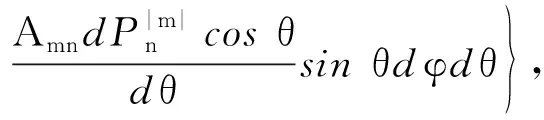
(6)

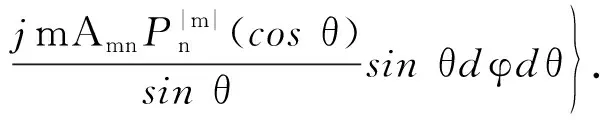
(7)

在远区场可以对球汉克尔函数及其导数进行大宗量近似来处理,其近似表达式为:

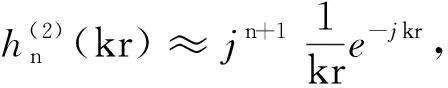
(8)

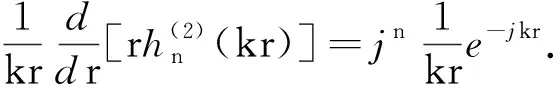
(9)

式(8)和式(9)中都包含了球面波因子e-jkr/(kr),因去除球面波因子后剩下的部分只与θ和φ有关,据此可以求得远场方向图函数的各分量为:

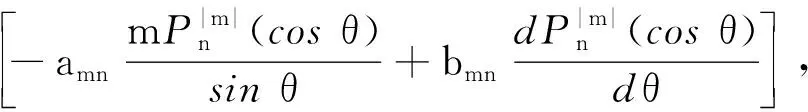
(10)

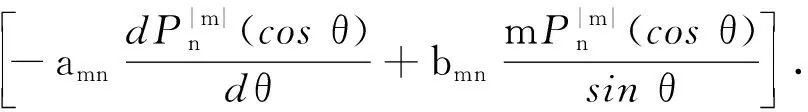
(11)

则远场方向图函数为

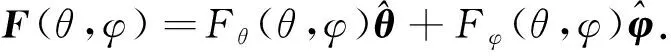
(12)

2 余弦窗函数

在实际测量中,由于近场数据采集不完整,而在球面上通过积分求解模系数时只能把未采集到的数据设为零,这就意味着求解积分时待测天线在未采样区域的辐射场是不正确的. 这种数据在采集区域到未采集区域的突然不连续性形成了截断误差. 研究发现,在球面近场测量中对包含在截断区域的近场数据进行加窗处理可以有效地减小截断误差,让测量精度达到预期要求. 本节从数字信号处理的思路出发,将窗函数应用在相控阵天线球面近场测量中来减小截断误差.

由采样定理可知,对于一个有限带宽的模拟信号xa(t),如果采样信号的角频率大于或等于该信号角频率的两倍,则该信号可以由抽样值唯一表示. 设采样信号为pδ(t),则采样后的信号可以表示为

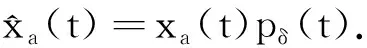
(13)

对式(13)两边取傅里叶变换得

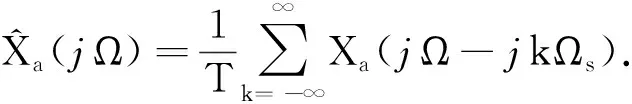
(14)

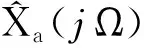
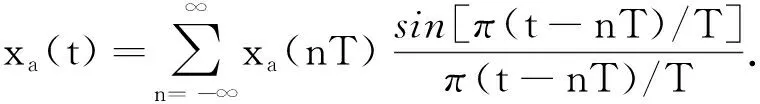
(15)

该式即为内插函数,它表明了模拟信号如何通过采样信号恢复,即原模拟信号等于采样值乘以对应的插值函数的和.

内插函数可以看作是原采样信号的加权函数,即对各个采样点加了权值,加权函数也称为窗函数.在球面近场测量中,对包含在截断区域的近场数据加窗时,应同时考虑对其幅度和相位加窗.

窗函数的类型有很多,这里重点对余弦窗函数做介绍．

余弦窗函数的幅度分布和相位分布如图1所示,x%是单侧加窗范围占整个采样范围的百分比,dmp是最大相位延迟. 设一个方向采样总点数为N,采样间隔为dθ,因此采样长度为W=(N-1)dθ,设

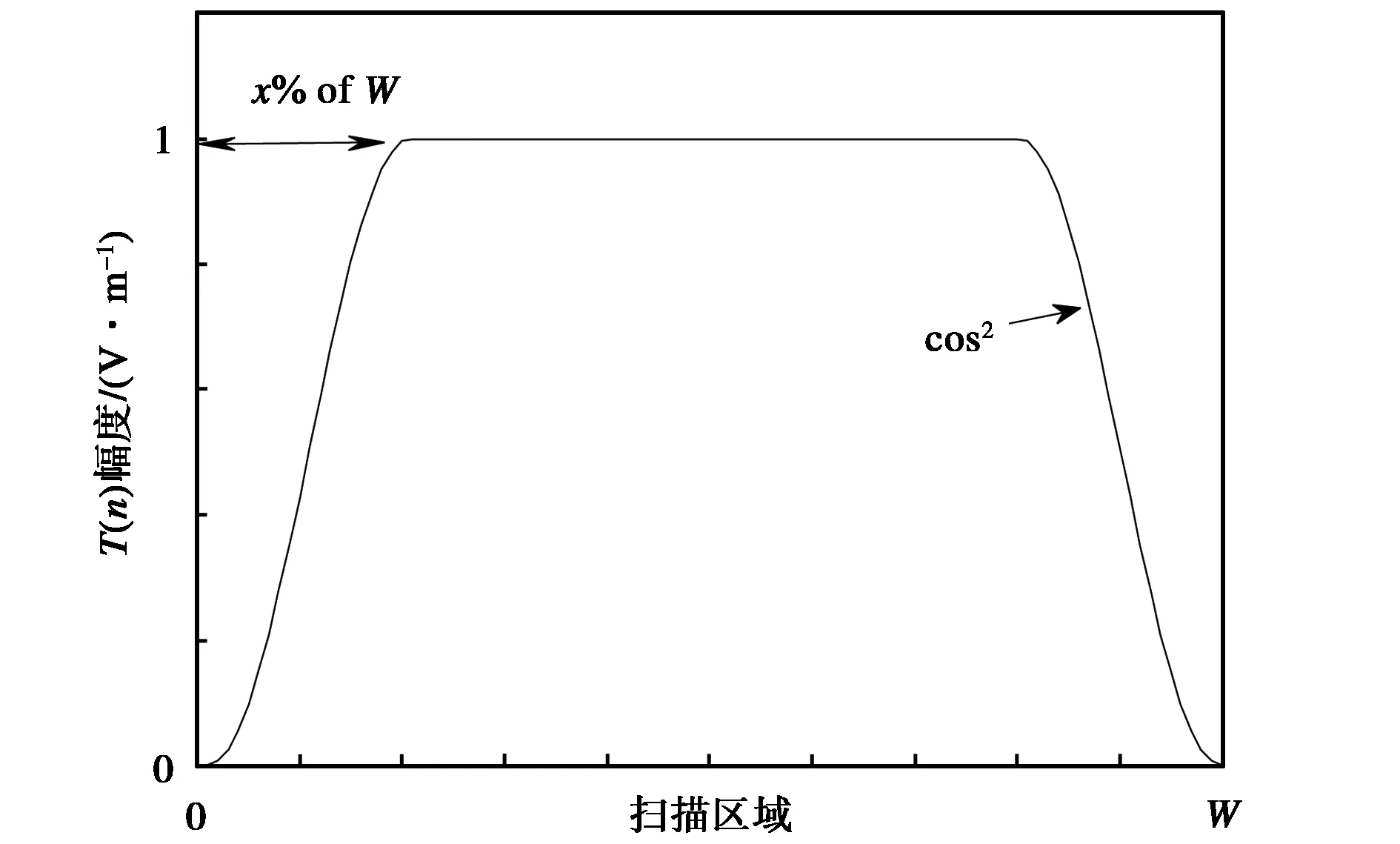
(a) 幅度分布(a) Magnitude of T(n)

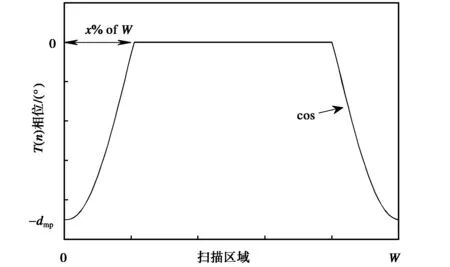
(b) 相位分布(b) Phase of T(n)图1 余弦窗函数的幅度和相位分布Fig.1 The magnitude and phase distribution of the cosine window function

余弦窗函数的表达式为

T(n)=A(n)ejP(n).

(16)

式中,n=1,2,3,…,N;A(n)为幅度;P(n)为相位,它们的表达式为

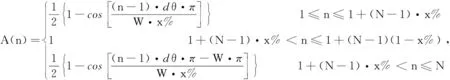
(17)

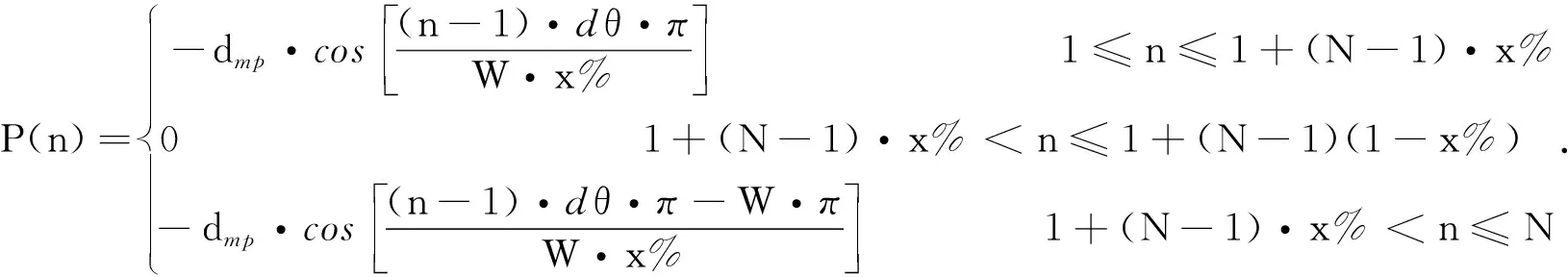
(18)

因为余弦窗函数是一个复数窗,既包含了幅度,又包含了相位. 而近场数据也是复数,因此要考虑到既对幅度加窗,也要对相位加窗. 还应该注意的是加窗方式[10],对于包含在截断区域的球面采样数据既可以在θ方向加窗,也可以在θ和φ方向同时加窗. 由于本文中的例子只在θ方向引入了截断误差,为了方便说明窗函数对减小截断误差的作用,文中的所有加窗均只在θ方向加窗,如图2所示.

图2 一种沿θ方向的加窗方式Fig.2 A method of window weighted along the θ direction

3 计算机仿真

本文以半波对称振子阵列为天线模型,来验证球面近远场变换的正确性. 如图3所示,半波对称振子阵列位于xoy平面上, 且振子单元沿x轴方向

放置. 设振子在x方向放置的个数为M′=13,间距为dx=0.7λ(λ为波长);在y方向放置的个数为N′=9,间距为dy=0.7λ,对称振子单元的编号如图3中所示. 设阵列单元沿x方向和y方向的波腹电流分布分别为-55 dB副瓣的切比雪夫分布和余弦分布. 该半波对称振子阵列的理论近场数据可由文献[11]求得,理论远场方向图可由文献[12]求得.

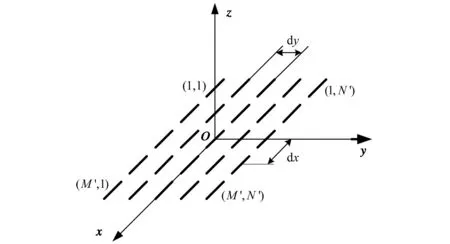
图3 半波对称振子阵列模型Fig.3 The half-wavelength dipole array model

3.1 余弦窗函数的应用

设该阵列天线在近场数据的截断角为θt=45°,不失一般性,设天线最大辐射方向为θ=20°,φ=0°. 在有限扫描面和整个采样球面情况下,球面近远场变换所得远场方向图如图4所示. 从图中可以看出,当采样面为整个球面时,球面近远场变换结果和理论值吻合较好,从而证明了该球面近远场变换的正确性,而只采集部分近场区域时引入了较大的截断误差.

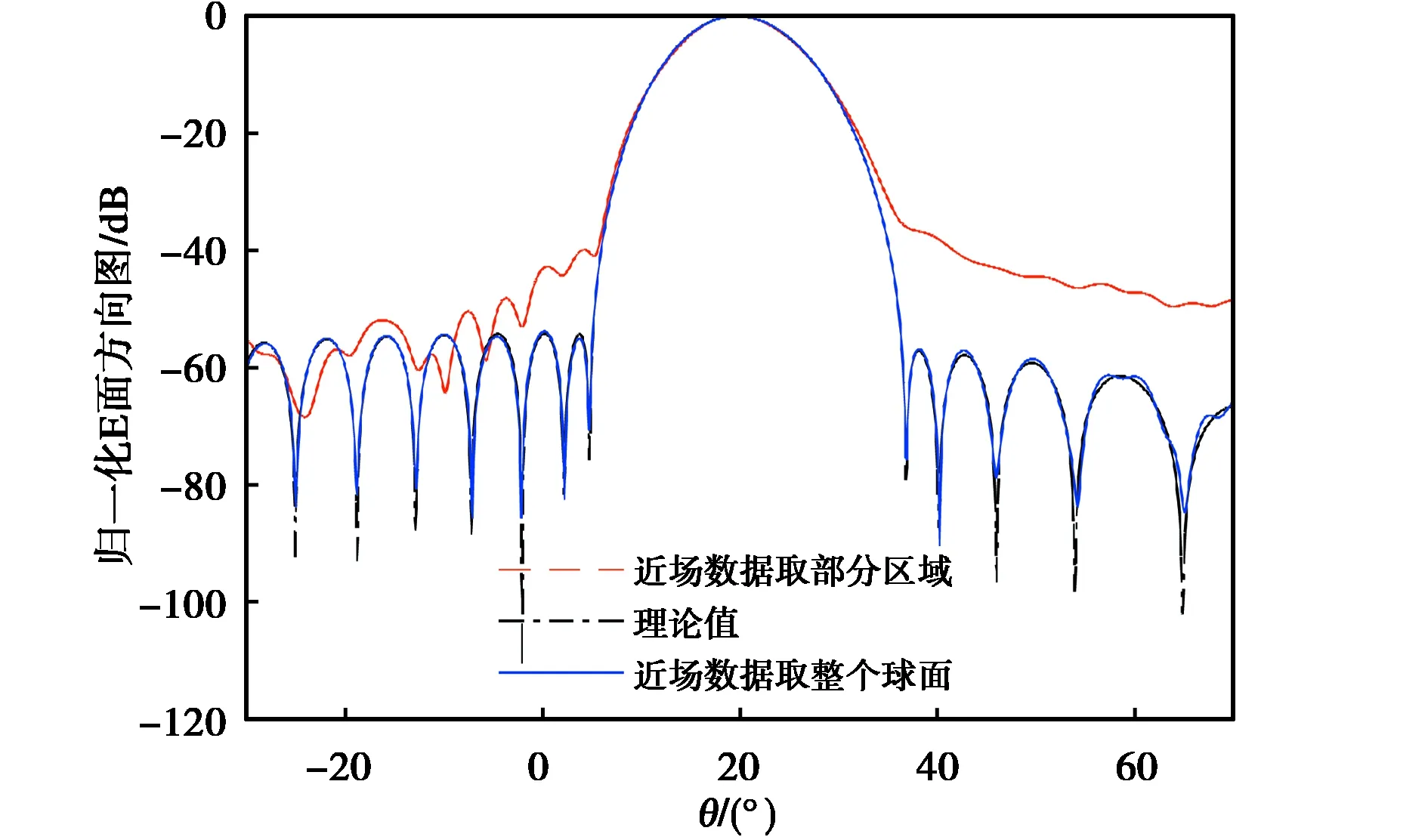
图4 利用不同近场数据区域的球面近远场变换所得E面方向图Fig.4 The E-plane patterns by spherical near-field to far-field transformation with different data region

现在考虑对近场数据进行加余弦窗函数处理后,再做近远场变换. 取余弦窗函数的参数为x%=40%,dmp=1°,最终的计算结果如图5所示.

图5 对近场数据加窗后的球面近远场变换所得E面方向图(x%=40%, dmp=1°)Fig.5 The E-plane pattern by spherical near-field to far-field transformation with near-field data weighted by cosine window function(x%=40%, dmp=1°)

从图5可以看出,对近场数据加窗后再做近远场变换得到的远场方向图更接近理论值,主瓣相对不加窗有改善,在副瓣部分效果特别明显,其量化误差统计如表1所示.现在改变窗函数参数,其他保持不变,取x%=32%,dmp=0°,计算结果如图6所示,误差分析如表2所示.

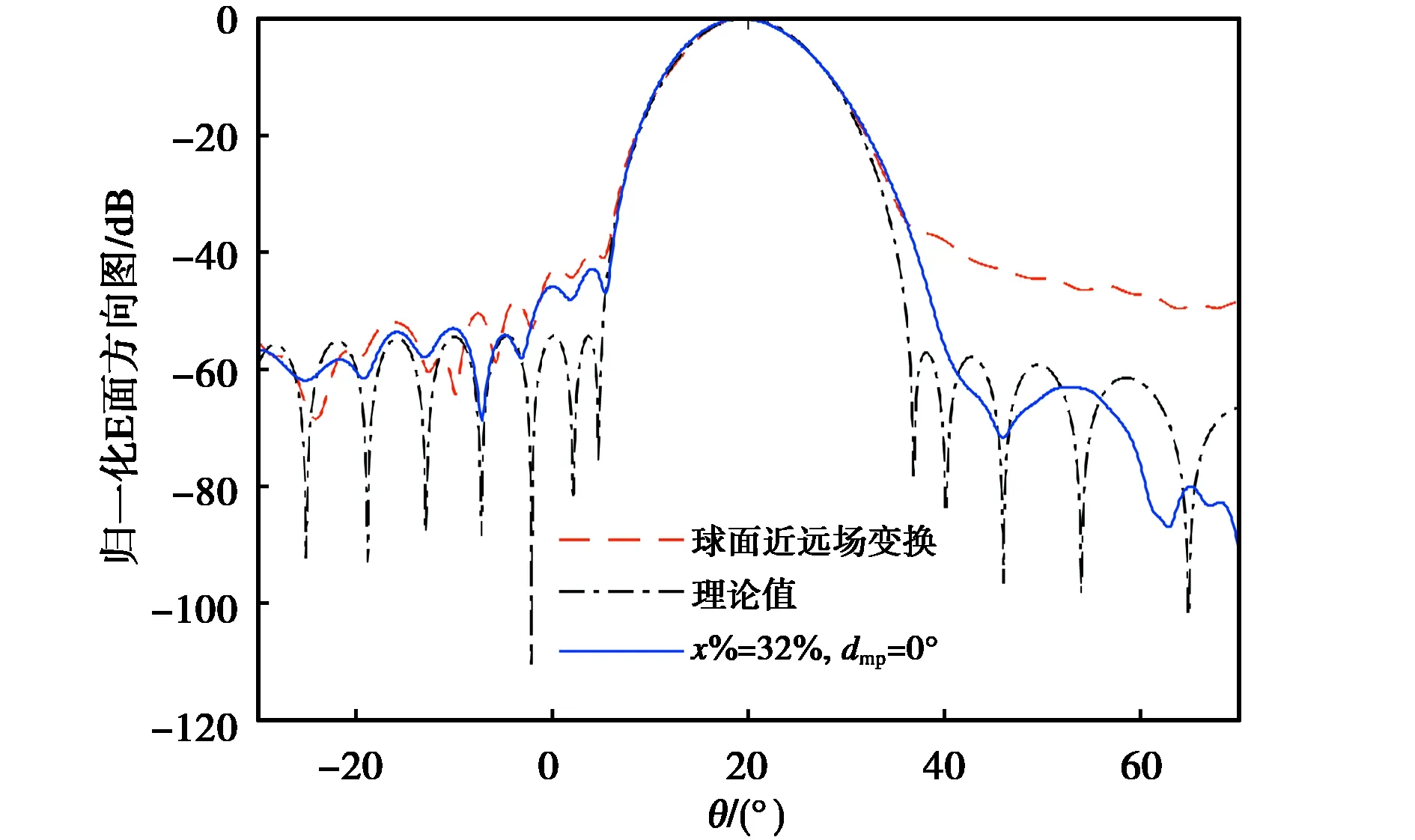
图6 对近场数据加窗后的球面近远场变换所得E面方向图(x%=32%, dmp=0°)Fig.6 The E-plane pattern by spherical near-field to far-field transformation with near-field data weighted by cosine window function(x%=32%, dmp=0°)

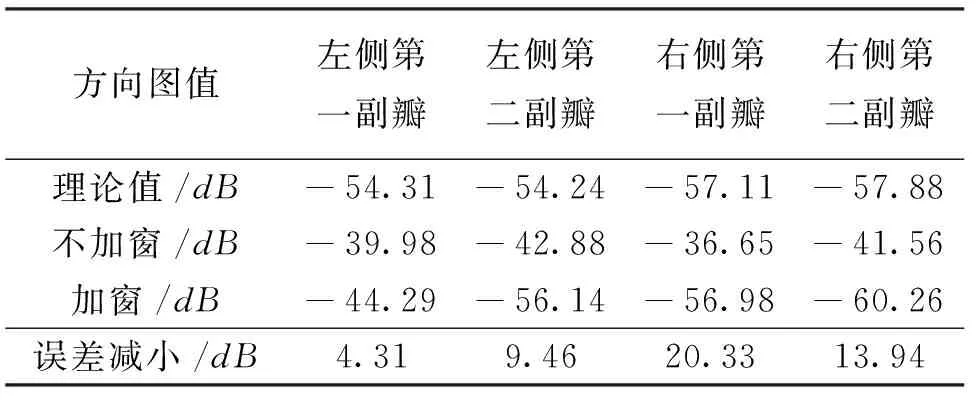
方向图值左侧第一副瓣左侧第二副瓣右侧第一副瓣右侧第二副瓣 理论值/dB-54.31-54.24-57.11-57.88 不加窗/dB-39.98-42.88-36.65-41.56 加窗/dB-44.29-56.14-56.98-60.26 误差减小/dB4.319.4620.3313.94

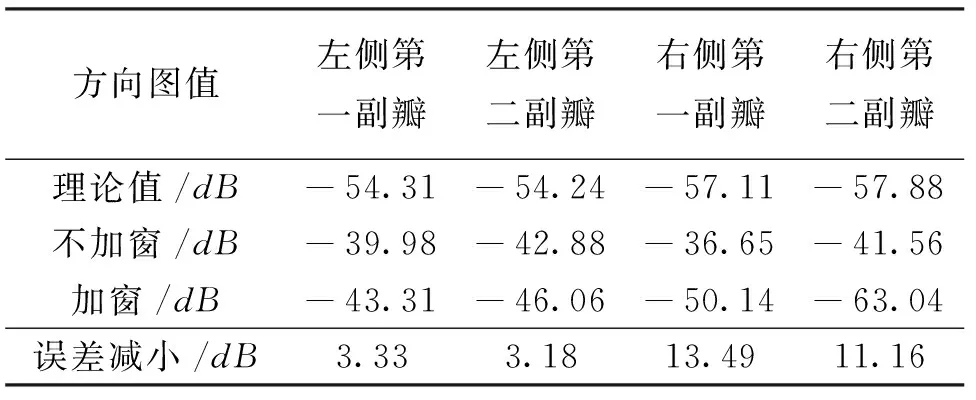
表2 x%=32%, dmp=0°时误差分析Tab.2 Error analysis when x%=32%, dmp=0°

从表1可以看出,不对近场数据加窗时,球面近远场变换所得方向图在左侧第一副瓣处的值比理论值高14.33 dB,当取窗函数参数为x%=40%,dmp=1°时,对近场数据加权处理后,相对于理论值,误差减少了4.31 dB. 在左侧第二副瓣处,对近场数据加窗后球面近远场变换所得方向图的值由-42.88 dB减小到-56.14 dB,相对于理论值,误差减小了9.46 dB. 而在主瓣右侧, 这种方法对误差的减小更为明显,在右侧第一副瓣处,对近场数据加窗后所得方向图的值由-36.65 dB减小到-56.98 dB,相对于理论值,误差减小了20.33 dB;同时在右侧第二副瓣处,误差减小了13.94 dB,这是因为在右侧采样面边缘附近,由于近场数据的不连续性引入的截断误差较大,而余弦窗函数在边缘处对近场数据的加权程度也相应加大,使得误差大大减小,这正是利用余弦窗函数对近场数据加权的优点. 通过比较表1和表2可以看出,当选取的窗函数参数不同时,近远场变换的最后结果会不同,因此选取合适的窗函数参数可以使截断误差降低到最小.

当天线最大辐射方向改变为θ=30°,φ=0°,而其他参数保持不变时,设截断角θt=55°,取x%=36%,dmp=3°,计算结果如图7所示.从图中可以看出,对包含在截断区域的近场数据加窗后再做近远场变换可以明显地改变副瓣电平,使副瓣电平更接近理论值,通过计算发现,当天线最大辐射方向与扫描面边界距离越近时需要加窗程度也越强.

图7 对近场数据加窗后的球面近远场变换所得E面方向图(x%=36%, dmp=3°)Fig.7 The E-plane pattern by spherical near-field to far-field transformation with near-field data weighted by cosine window function(x%=36%, dmp=3°)

3.2 遗传算法的应用

通过上节的分析可以看出,对于不同的天线最大辐射方向和扫描面边界,需要选取一个最合适的余弦窗函数参数,本节利用遗传算法来选取最优窗函数参数.

遗传算法是一种全局随机搜索优化算法[13-14],本例中将遗传算法交叉概率设为0.6,变异概率设为0.001,种群的规模大小为80,遗传迭代的代数为400. 设余弦窗函数参数的优化精度:x%为0.1%,dmp为1°,编码方式为二进制编码.令适应度函数为

Fitness=∑|F理论值(θ,φ)-F测量值(θ,φ)|2.

(19)

式中:F理论值(θ,φ)为理论远场方向图;F测量值(θ,φ)为测量远场方向图.取x%的搜索范围为[0, 50%],dmp的搜索范围为[0, 360°]. 天线模型与上节保持不变,取最大辐射方向为θ=30°,φ=0°,截断角θt=55°,计算结果如图8所示.

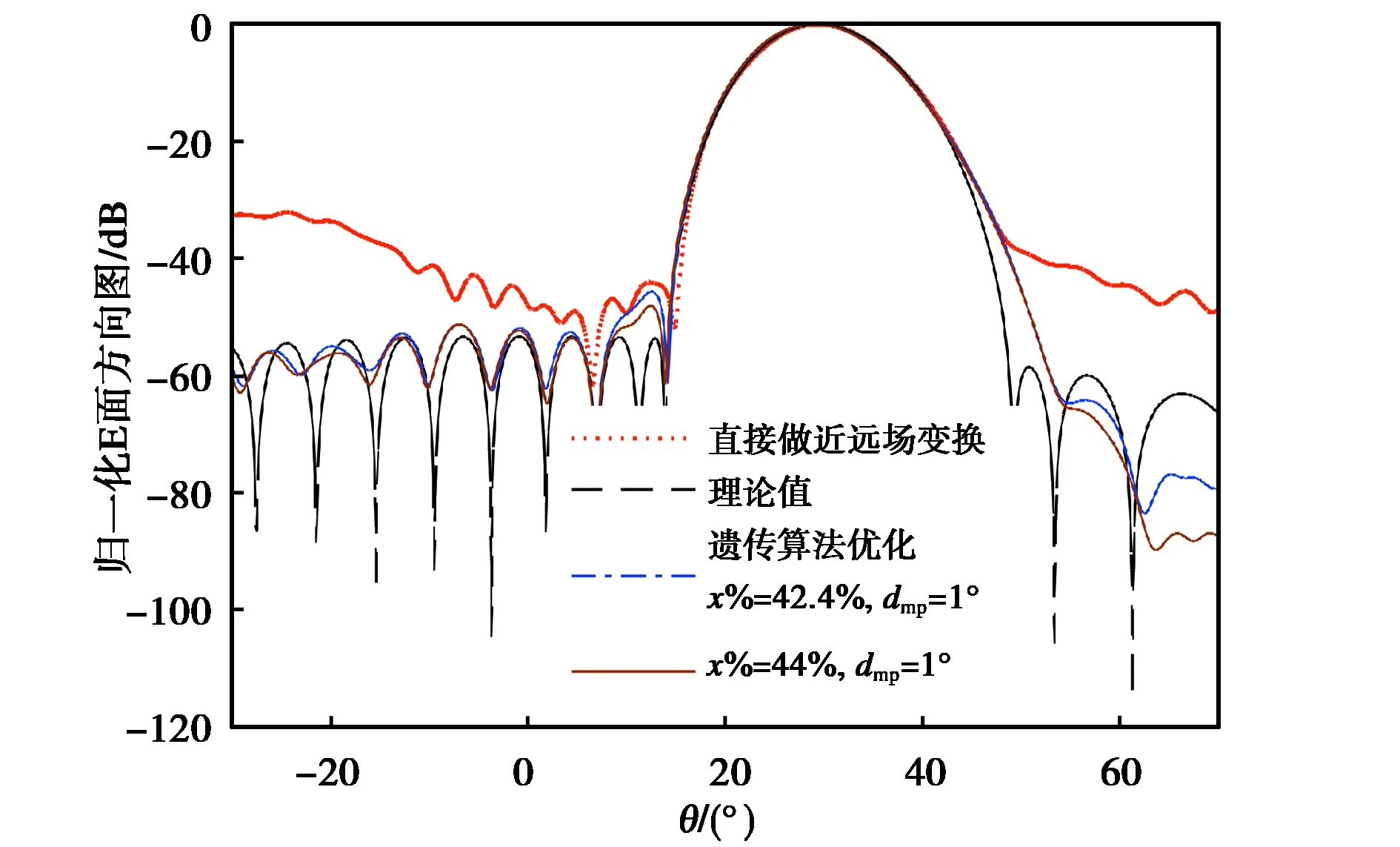
图8 遗传算法和穷举法的对比Fig.8 Comparison of genetic algorithm and exhaustive method

从图8可以看出,利用基于遗传算法参数优化的余弦窗函数对近场数据进行加权处理能够大大减小有限扫描面截断误差.遗传算法搜索的最优解与穷举法得到的最优解较为接近,但是使用遗传算法可以减少程序运行时间.其中主瓣左侧吻合得较好,而主瓣右侧吻合得相对较差,这是因为天线最大辐射方向在z轴右侧,扫描面右侧边界处的场较强,导致扫描面右侧边界处场的不连续性比左侧边界处的不连续性更强,从而导致方向图主瓣右侧的截断误差比左侧大. 表3给出了几种不同情况下利用遗传算法得到的最优窗函数参数的具体取值.

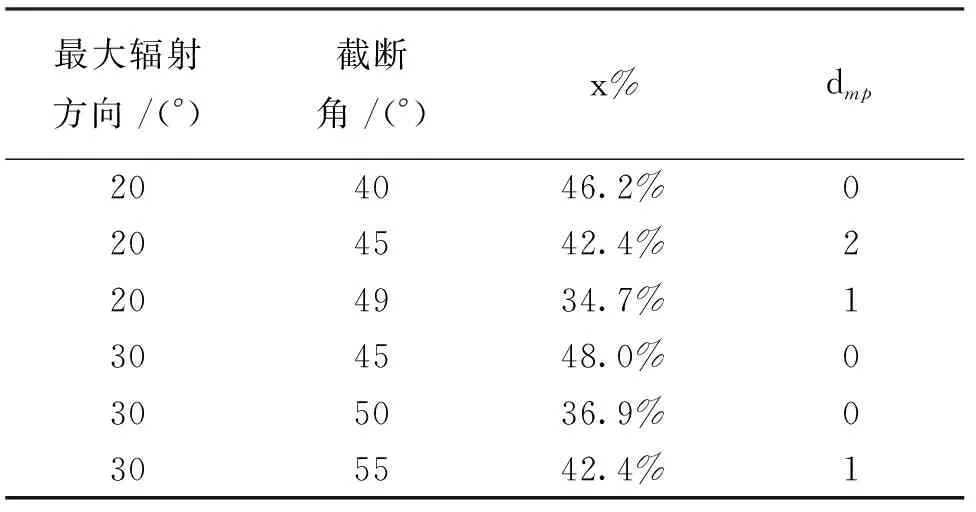
表3 不同情况下的最佳参数选择Tab.3 Selection of optimal parameters in different cases

4 结 论

本文针对相控阵天线球面近场测量时,由于扫描面有限和波束扫描引起较大的截断误差这一问题,提出了利用余弦窗函数对近场数据进行加权处理的方法来减小截断误差. 相比于其他方法,由于窗函数参数的灵活性,当相控阵天线发生波束扫描及截断角发生变化时,可以根据不同的情况确定最佳窗函数参数使截断误差降到最小,尤其是在副瓣处修正效果更明显,具有实际工程意义. 对于窗函数参数的选取,遗传算法的应用可以提高参数优化效率,得到最优参数,从而大大减小截断误差.