非谐振多层级联频率选择表面研究

党涛 田殷 王辂 王光明 郑宏兴

(1. 空军工程大学防空反导学院,西安 710051; 2. 河北工业大学电子信息工程学院,天津 300401)

引 言

隐身技术对现代武器装备具有重要的意义,相应的隐身作战平台也应运而生. 随着多功能系统和低可探测平台的出现,良好的设计使装备的雷达散射截面(radar cross section, RCS)降低,大幅提高了作战平台的战场生存能力. 隐身要求的频率范围通常为2～18 GHz. 然而在实际应用中,工作在L波段的天线阵列,对高于其工作频率范围的电磁波呈现较强的散射,成为重要的雷达回波源,破坏了整机的隐身性能.

频率选择表面(frequency selective surface, FSS)能够减小工作频带外较宽范围的散射,从而缩减带外RCS. 而天线工作频率范围内的信号可以几乎无损耗地通过FSS,以保证天线的正常工作. 它还可以在电子对抗中起到抗干扰的作用. 因此,研究FSS使其在保持结构隐身设计的同时,对不同频率的电磁波“透明”和“阻止”,对于降低装备的RCS意义重大.

近年来随着计算机技术的进步,一方面可以建立精准的物理模型,另一方面也使得对FSS严格的数值分析成为可能. 人们在掌握原有形式单元的基础上,开发出更具特色的FSS单元,如高Q值、高频率选择特性、双频段等. 同时印刷电路技术的发展,使得对它的研究为改善性能和实际应用提供了实现的可能. 最具代表性的是Wright-Patterson航空电子实验室的FSS[1],在8.8～9.0 GHz频带内传输特性有很好的入射角稳定性和交叉极化特性,并可以在其内部安装能发射任意极化信号的扫描天线,还可减轻带外电磁波干扰所带来的影响,避免带外电磁波在机载雷达天线上产生感应电流而向外产生较大的辐射,减少飞机在机头方向上的RCS. R. Mittra教授的研究组率先提出了分析FSS的谱域法,并用这种方法分析了具有不同周期的多层级联平面[2-3]. 其他研究小组给出了具有工程应用价值的不同形式单元形状的等效电路,并对构成FSS的诸多参变量对频响特性的影响进行了讨论[4-5]. 人们还对多频段频分复用天线进行了研究:应用同心环贴片的组合设计了一系列从双频段到四频段应用的FSS[6-8];利用分形几何结构设计多频段FSS[9];在设计中加入优化算法,获得一系列高性能的FSS单元[10]. 近几年,基片集成波导技术被应用于FSS中[11],通过在级联的多层FSS之间打金属通孔,有效提高了通带的陡峭度和带外抑制度,将有源器件应用在FSS中,或提升FSS入射角稳定性和交叉极化特性,实现宽角入射,或形成一种可调的新的吸波结构体.

目前,带通型FSS会在单元谐振频率的倍频及以上出现高次谐振模式及不同阵列之间的相互干扰,破坏其阻带性能[11]. 现有研究虽然可以实现通带内较好的传输性能,却无法实现带外超宽带的反射特性,尤其是应用在低频的FSS,采用谐振单元不易实现超宽阻带. 为解决这一问题,本文提出了一种基于耦合滤波器理论的方法,通过电容层、电感层等非谐振单元组成多层级联结构,将电路的T型网络变换为Π型网络,形成电感耦合高阶带通滤波响应. 组成的谐振频率不在所观测的频率范围内,由这种“非谐振单元”组成的级联结构可以在很宽的频率范围内不产生高次谐振模式,甚至不产生基本谐振模式,从而加大阻带带宽. 上述设计用实验进行了验证,达到了预定的目标.

1 单元结构设计

按照机载天线的工作频率,FSS技术指标如表1所示,要求通带频率为0.9～1.2 GHz,中心频率1.05 GHz,相对带宽28.6%. 对于低频宽带FSS,有谐振型级联结构和非谐振型级联结构两种类型. 谐振型级联结构的组成单元为缝隙型带通FSS,金属单元自身即可谐振在所需的工作频率,通过两层或者多层金属单元级联拓展带宽,金属层之间由介质材料填充[12]. 非谐振型级联结构通常至少由三层金属层组成,两层电容层和一层电感层,其中电容层和电感层自身均不可在所需工作频率谐振,金属单元自身的谐振频率远高于工作频率,而三层金属层组合在一起时,可以谐振工作在低频. 根据Foster电抗定理[13],单元的传输极点和传输零点是交替分布的,因此高阶谐振模式会对阻带造成破坏. 对于阻带抑制较宽的FSS,通常要求抑制频带范围超过几倍通带中心频率甚至十几倍通带中心频率. 非谐振型级联单元的组成周期通常可以小于1/15工作波长,因此,即使要求的阻带抑制频率范围较宽,也可以实现在宽频带范围组成单元不出现高阶谐振模式和栅瓣. 以图1结构为例,电容层由金属贴片组成,电感层由金属网栅组成,金属贴片和金属网栅由介质基板分隔开,依次排布.

表1 FSS的技术指标Tab.1 Technical index of FSS

图1 非谐振型级联单元物理结构Fig.1 Physical structure of non-resonant cascading element

在高阶谐振模式出现之前,二维无限大周期贴片阵列可以用一个等效电容表示,二维无限大周期网栅阵列可以用一个等效电感表示,介质层则可以等效为传输线,那么图1中的结构可以等效为图2(a). 在传输线长度小于λ/12时,可以将其分布参数模型简化为一个串联电感和一个并联电容,等效后如图2(b)所示. 再将T型网络变换为Π型网络,即可得到电感耦合高阶带通响应,如图2(c)所示. 文献[14]根据非谐振单元的工作原理,设计了一个中心频率3 GHz级联带通FSS,并与相同尺寸的谐振级联单元进行比较,结果表明,非谐振单元的阻带特性良好,在观测频率范围内没有出现高次谐振或栅瓣,阻带光滑,通带带宽较宽. 因此,在下面的设计中,选择非谐振级联型单元实现设计目标.

(a) 二维无限大周期贴片和网栅阵列分别用等效电容和等效电感表示(a) 2D infinite periodic patches and grid arrays are represented by equivalent capacitance and equivalent inductance respectively

(b) 长度小于λ/12的传输线简化为一个串联电感和并联电容(b) Transmission lines less than λ/12 in length are simplified as a series inductance and shunt capacitance

(c) T型和Π型电感网络(c) T-and Π-type inductor networks图2 等效电路Fig.2 Equivalent circuit

2 宽带设计

指标要求的相对带宽为28.6%. 根据滤波器理论[15],二阶带通滤波器的带宽正比于等效电感与等效电容之比,因此在有限厚度的条件下,若要实现宽带频率响应,需要加大并联电感. 文献[16]中介绍了一种十字网栅结构的非谐振型级联结构电感层,在有限的周期和线宽条件下,有效限制了通带带宽. 在这种情况下,要想拓展带宽,则需要电感层获得更大的等效电感. 如果改变十字形结构,将十字网栅变为方形螺旋曲折线网栅结构,那么当二者具有相等的有效面积时,螺旋曲折线的电流路径明显得到延长. 此外,这种方式还可以通过控制单元尺寸以抑制高阶模式和栅瓣的出现.

考虑到物理尺寸的限制,需要在有限的面积下通过曲折线的方式延长电流路径以提高电感,因此金属条带排列紧密,电感层寄生电容效应较大(加大带内插损,两层电容层阵列干涉点提前出现). 由于电感层是平面结构,且单元之间相互连通,可以用两个相互正交的分离的金属条带代替之前的平面螺旋电感层,两层金属用介质板加载. 下面的仿真主要采用这种电感层形式.

3 阵列干涉

虽然非谐振型级联单元的阻带特性较好,但如果使用厚介质层以降低大角度入射时的插入损耗,可能会在高频出现寄生通带,如图3所示. 通带中心频率为2.36 GHz,第一和第二寄生通带分别出现在17.69 GHz和27.88 GHz,这并不是由于其金属单元的高阶谐振或单元的栅瓣造成,而是因为金属层之间产生了相互干涉,即阵列干涉. 其效果类似于枝节匹配器,在某些特殊的频点上,跨接在传输线上的导纳经过多节传输线之后,产生了近似匹配的效果.

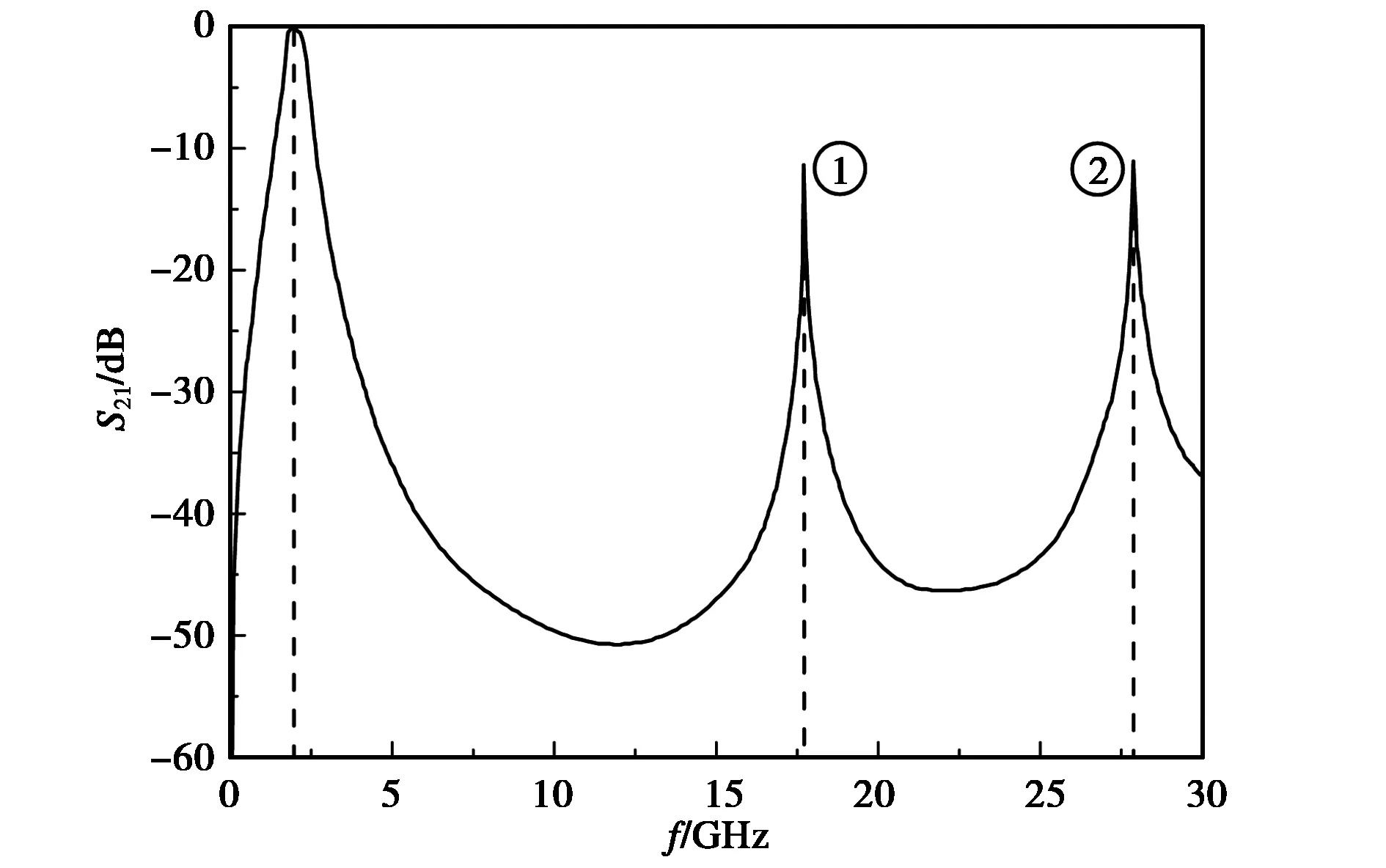
图3 非谐振型级联单元的阵列干涉现象Fig.3 Array interference phenomenon of non-resonant cascading element

非谐振型级联结构如图4所示,为抑制这种结构中的阵列干涉,采用修改电容层金属图案的方法. 贴片的等效电路可以用结电容表示,方环的等效电路可以用串联LC网络表示,因此方环单元为带阻型单元,如图5所示.

图4 非谐振型级联结构Fig.4 Non-resonant cascading structure

(a) 贴片 (b) 方环 (a) Patch (b) Square loop图5 贴片和方环的物理模型及其等效电路模型Fig.5 Physical model and equivalent circuit ofpatch and square loop

那么,将图4所示结构中的电容层1和电容层2改进为谐振型的方环单元,如图6所示,并通过调整方环的尺寸,将它们的传输极点置于阵列干涉点处,这样可以有效抑制由阵列干涉造成的窄传输峰. 在低频,电感对阻抗的贡献较小,因此在低频贴片单元和方环单元的导纳相近, 二者所构成的非谐振型级联结构通带特性基本一致;而在高频,二者的导纳和传输特性相差较大,方环电容层可以有效抑制高频干涉,如图7和图8所示. 方环电容层构成的非谐振型级联结构在高频处出现传输峰,在保持通带特性的同时,提高了阻带性能,拓展了阻带带宽. 进一步,可以根据当前结构,合理设置电容层和电感层的物理尺寸,实现所要求的电性能指标. 在下一节的实验设计过程中,就选用这种方环电容层和螺旋曲折线电感层构成的非谐振级联结构.

(a) 电容层1 (b) 电容层2(a) Capacitive layer 1 (b) Capacitive layer 2图6 电容层1和电容层2的改进结构Fig.6 Improved structure of capacitive layer 1 and layer 2

图7 贴片电容层和方环电容层构成的非谐振型级联结构的传输特性Fig.7 Transmission characteristic of non-resonant cascading structure with patch and square loop capacitance layer

图8 贴片电容层和方环电容层的导纳Fig.8 Admittance of patch and square loop capacitance layer

4 实验结果

对上述结构进行优化,单元周期3.52 mm,厚度20.8 mm. 介质1为陶瓷材料,介质2为泡沫材料,介质3为Rogers 5880,电感层线宽为0.1 mm,金属层和介质层的结构参数和物理参数见表2和表3,用印刷电路板工艺加工.

表2 单元结构的尺寸Tab.2 Structure parameters of elements mm

表3 单元结构的物理参数Tab.3 Physical parameters of elements

传输通带工作的极化方式为TE极化,阻带抑制为TE和TM极化. 采用矢量网络分析仪测得结果如图9和图 10所示,其中图9(a)和图10(a)为整个通带内的传输特性,图9(b)和图10(b)为设计标准所要求工作频带内传输系数的局部放大.

可以看出,随着入射角加大,TE极化的通带轻微上偏,通带低频插损加大,通带中心凹陷加大. 在2～18 GHz阻带频率范围,TE极化阻带抑制良好,可以满足在2～18 GHz抑制大于15 dB的要求. TM极化时,随入射角加大,谐振频率上偏,矩形系数降低带外抑制变差. 但是TM极化阻带抑制均值大于15 dB. 表4列出了TE极化和TM极化分别以0°和30°在不同频率下入射所得到的仿真和实测结果的采样对比,可以看出二者保持很好的一致性. TE极化通带插损均值和TE、TM极化阻带抑制均值如表5和表 6所示. 结果表明这种结构在通带0.9～1.2 GHz范围内的0° ～70°内有着良好的传输特性,满足了控制飞行器平台的需求.

(a) 全频带(a) Full-band

(b) 通带(b) Passband图9 TE极化传输特性Fig.9 Transmission characteristic of TE mode

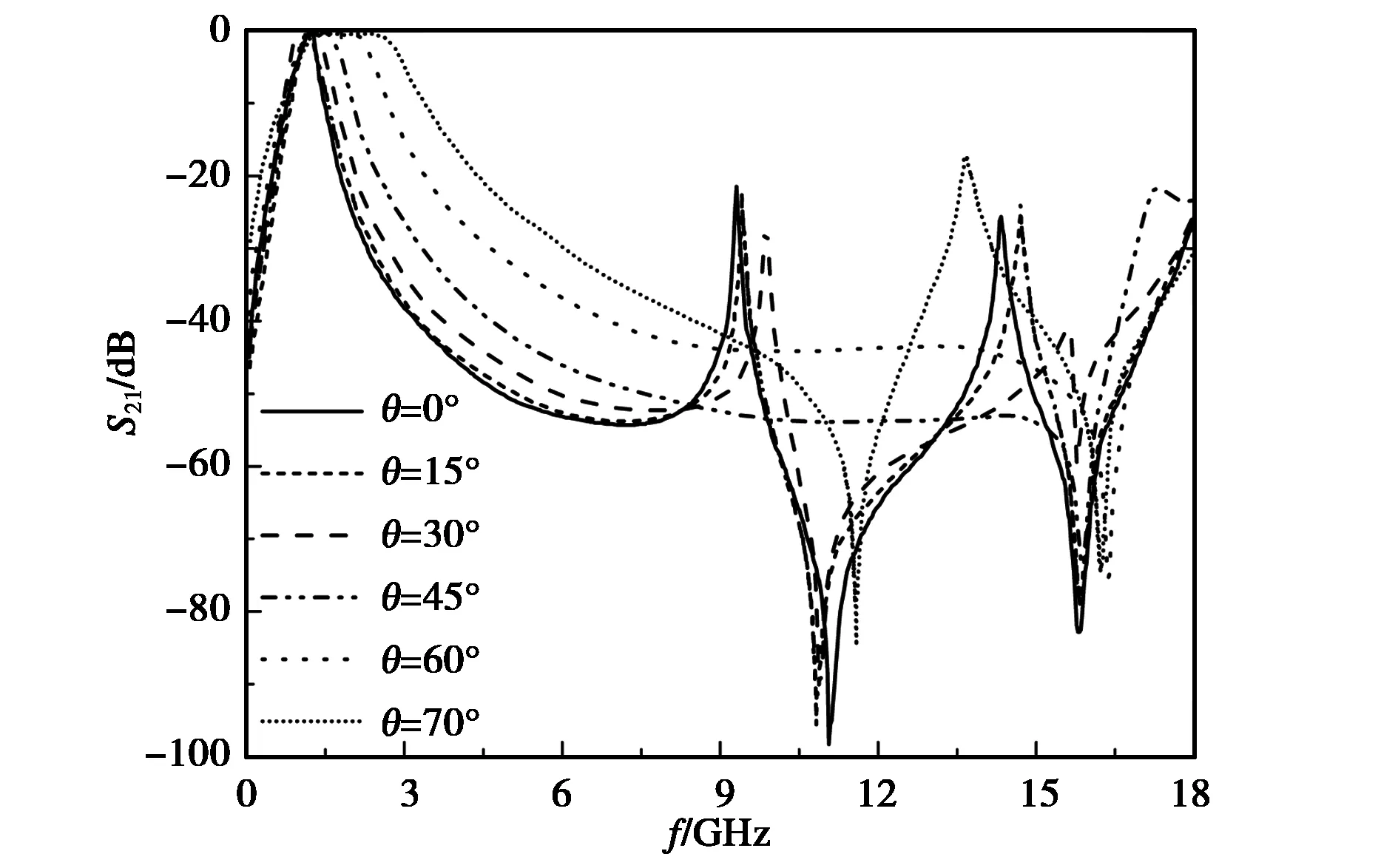
(a) 全频带(a) Full-band

(b) 通带(b) Passband图10 TM极化传输特性Fig.10 Transmission characteristic of TM mode

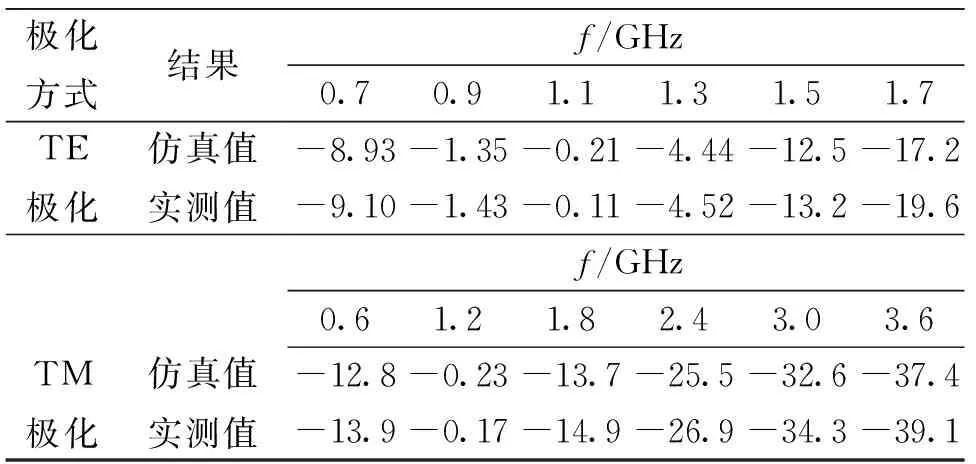
表5 0.9～1.2 GHz频段TE极化通带插损Tab.5 Passband insertion loss of TE mode in 0.9—1.2 GHz

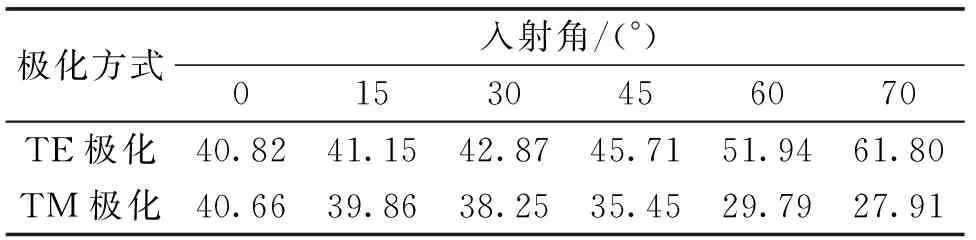
表6 0.9～1.2 GHz频段阻带抑制Tab.6 Stopband rejection in 0.9—1.2 GHz dB

5 结 论

以飞行器天线阵列隐身技术为研究对象,通过理论分析和仿真比较,详细讨论了控制RCS的有效方法. 外形设计是降低RCS的有效手段,但由于飞行器平台的特殊性时常不能完全满足设计要求. 而频率选择表面则能够在保证通带良好性能的条件下,达到较高的阻带指标. 总结出了用非谐振方环代替谐振贴片设计频率选择表面的方法,仿真结果表明用该方法所设计的频率选择表面通带和阻带特性都有显著提高.

在线学习文献对于互动的重要性一致认可，人们相信学生、教师与学习内容之间的互动在所有正式教育中都发挥着基本的作用。如图1所示，技术支持下的在线教育学习空间构成中，静态技术如视频、文本和网页等，使学习者能够获取或观看稳定的信息，但对学习者建构知识没有太多帮助。而在线教育的动态教学环境下，位于连续体中间技术如弹幕、讨论区和博客等，使学习者能够与内容及其他学习者、教师进行互动交流、评价和回应。教师在这一过程中引导学生将问题和现有知识表征进行比较，通过分析与辩论，促进学生构建自己的反应，形成新的认知。