光场熵：针对光场编码的客观评价指标

2018-09-12胡舒童郭碧川

计算机与生活 2018年9期

胡舒童，郭碧川，王剑

1.清华大学电子工程系，北京 100084

2.清华大学计算机科学与技术系，北京 100084

1 引言

现代意义上的光场由苏联科学家Gershun所定义[1]，它描述了空间中任意位置、方向、时刻、任意波长的光的信息。最初的光场模型具有最一般的形式，总共包含7维的信息；经过一系列简化[2-3]之后，最初的光场模型被简化为一个4维模型，记为L(u,v,x,y)，代表光线的集合分别与两个平行平面uv、xy相交于点(u,v)与点(x,y)[4]。

近年来商用光场相机技术有了显著进展，以LytroIllum为代表的消费级光场相机大大拓宽了研究者获取光场数据的途径。由于光场图片原始数据的4维结构引入了很大的冗余性，对光场图片进行压缩编码对于光场图片的存储以及后续处理来说是不可或缺的环节。同时，近年来的部分光场相机能在拍摄时获取除传统的颜色通道以外的额外的像素置信度信息[5]。此置信度信息可视作光场图片数据的可信度，因此会影响对光场编码算法的客观评价。在光场编码的客观评价中，大多数研究者使用峰值信噪比（peak signal-to-noise ratio，PSNR）与结构相似性（structural similarity index，SSIM）作为客观指标度量编码算法的性能，虽然此两种指标可度量有损编码的重建质量，但却忽视了前文所述光场中像素置信度的变化。

针对以上问题，本文提出了一个针对光场编码客观评价的新指标，称作光场熵。此指标将上述光场图片的置信度通道纳入了考量，可看作光场编码的总信息损失。为计算此指标，光场子孔径图中任意像素被建模为基于自身置信度的随机变量；虚拟视点由一种简单且鲁棒的光场渲染方法插值得到[2]；压缩损失则被建模为每个像素点随机变量分布的偏移；Kullback-Leibler散度（Kullback-Leibler divergence，KL散度）[6]则用来量化分布的偏移，其针对光场所有子孔径图的所有像素点的累积值及其对数表示即为本文所提出之新指标光场熵。

为了证明本文所提出新指标在光场编码客观评价中优于传统指标，进行了完整的光场编码质量评价实验：使用新指标与传统指标PSNR针对数种已存在的光场编码算法进行客观评价实验，同时针对相同的实验材料进行相应的主观测试。客观实验与主观测试的结果显示，本文所提出的新指标光场熵对光场编码的评价结果，与PSNR相比，与人眼主观测试的结果之间具有更高的相关性，因此可以说明其预测人眼主观感受的性能比传统指标PSNR更优。

本文组织结构安排如下：第2章给出相关工作介绍；第3章详细讨论了基于置信度的随机模型、插值生成新视点以及光场熵的数值计算；第4章给出详细的光场编码评价实验结果以及相关讨论；第5章总结全文。

2 相关工作

文献[7]介绍了多种不同的光场图片采集技术，这些技术可分为3类[8]：多传感器捕捉[9]、时间序列捕捉[10]、复用成像捕捉[11-12]。其中空间复用捕捉方法中的微透镜阵列解决方案为未来商业应用中最有前景的一种光场捕捉方案，因其尺寸微小，可集成于移动设备之中。

光场渲染在光场图像处理中具有关键意义。文献[2]展示了一种经典的光场渲染方法，通过重采样与插值光线来生成光场的虚拟渲染。文献[13]介绍了一种基于几何信息的渲染方法，通过利用光场图像的深度信息，渲染所需的插值光线可显著降低。

文献[4]描述了光场编码领域中数种前沿的编码算法，这些编码算法可大致分为两类：（1）微透镜图像压缩；（2）透视图像压缩。后一种压缩算法中，光场图片的所有子孔径图被重新排列为伪时间序列的形式，并通过HEVC标准[14]视频编码器进行编解码；这一种编码算法又称作伪时间序列压缩。文献[4]中的评价实验结果显示，伪时间序列压缩算法性能优于微透镜图像压缩算法，并且重排子孔径图序列的顺序将对压缩算法的性能造成影响。

文献[4]针对上光场编码方法还进行了客观实验与主观测试。客观实验中，光场图片的每一张子孔径图及其对应的编解码后子孔径图的PSNR被分别计算，所有子孔径图计算得到的平均PSNR被用来作为指标分析光场编码算法的性能。然而这一计算仅仅基于少数整数坐标的离散视点（uv平面上15×15个离散点），而无法对具有连续坐标的全光场空间做出评价。并且由于PSNR在评价光场图像具有光学畸变的外围区域时的缺陷，在对PSNR的计算中，一部分子孔径图被人为弃置。因此在此客观评价中PSNR指标只能展示编码光场部分区域的编码质量。文献[4]进行的主观测试结果，通过假设检验方法分析处理后显示了人眼主观感受结果与PSNR指标所做出的客观评价有较明显的差异，因此说明PSNR未能较好地预测光场编码的性能。

本文的创新点主要为：提出一个度量光场编码带来的总信息损失的新客观指标。光学畸变引入随机性至观测到的光强之中，因此压缩损失以随机分布平均值偏移的形式体现。为计算压缩损失的具体值，引入KL散度衡量随机变量之间的距离。传统PSNR仅仅度量压缩损失，而本文新提出指标则进一步地将光场图像特有的光学畸变纳入考量。

3 光场熵指标模型

3.1 像素置信度与随机模型

采用微透镜阵列解决方案的光场采集设备在拍摄时将不可避免地引入光学畸变。此种畸变沿着uv平面上不同的视点而变化，视点越偏离图像中心，畸变约严重。此种光学畸变的严重程度可由一个额外的像素置信度通道来量化，如文献[5]中所述。典型的光场图像置信度分布如图1所示。

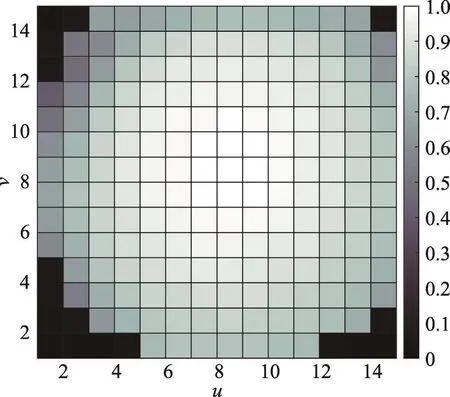
Fig.1 Distribution of confidence values图1 置信度分布

图1中每一个小方格代表uv平面上一张子孔径图中所有像素置信度值的平均。可观察到光场图像的中心具有最大的置信度，而光场图像的边缘角落置信度快速降低直至为零。在一张光场图片中，任意一个像素具有4个通道，即颜色三通道YUV通道以及像素置信度通道，此4个通道以一个四元坐标(u,v,x,y)所表示，可分别记为yuv(u,v,x,y)以及w(u,v,x,y)。以每一个像素点亮度的观察值Y作为条件，为了对光学畸变进行建模，引入正态分布来表示一个像素点亮度的真实值。由于真实分布应是单峰分布且以峰值对称，假设真实亮度分布的均值等于其观察值，而其方差则由像素的置信度所决定。值得一提的是，光场的编码仅仅影响光场图像的YUV三通道，而像素置信度则为一个固有的度量，其值仅由相机硬件设置所决定，并在编解码流程中保持不变。因此对光场图像中任意像素p及其对应的解码后像素p′而言，两者均服从正态分布。

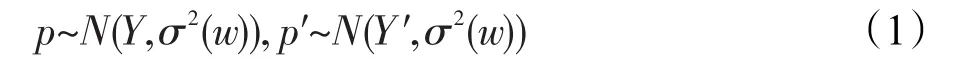
其中，w为像素置信度值；Y′为解码后像素点的亮度值。

本指标模型中，置信度值w被定义为在截断误差内正确观测到像素亮度的概率，即像素真实亮度值Yt∈(Y-0.5,Y+0.5)的概率。结合式（1），此概率计算公式如下：

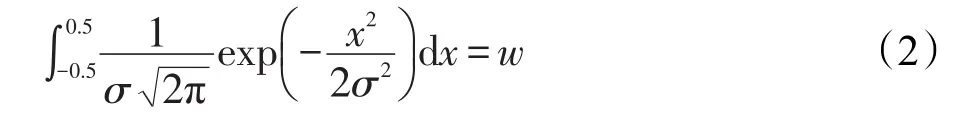
值得一提的是，由于截断误差的存在，式（1）中的方差具有一个最小值，而不会等于0，从而退化为确定性模型。由于亮度值总是离散的，因此(Y-0.5,Y+0.5)集合内的亮度值总是会被截断到Y。定义某一个像素点的置信度达到最大时，存在一个最小标准差σmin满足3σmin=0.5，使得最大置信度下采样亮度值Y落入区间(Y-0.5,Y+0.5)的概率在统计意义上3σ显著（约为99.73%）。

结合式（2），可以给出式（1）中标准差σ(w)的最终表达式为：

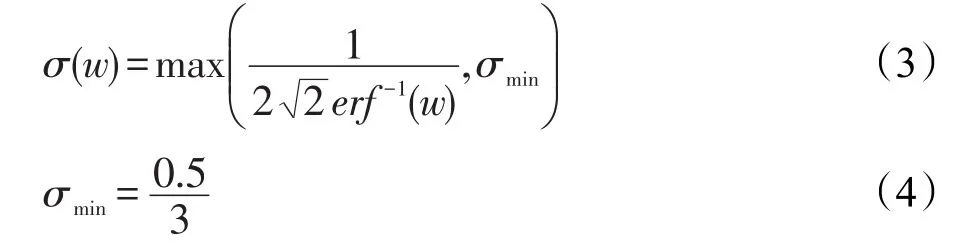
通过对光场图像中的每一个像素应用式（1）与式（3），可将光场图片中的每一个像素点随机模型化，且此随机模型同时考虑了压缩损失以及光场的光学畸变，直观地改良了PSNR指标的缺陷。

3.2 视点的插值生成

子孔径图为uv平面上有限的离散点观察到的光场子图像，可以直观地理解为在光场的四维表示L(u,v,x,y)中，固定坐标(u,v)后所观察到的一个特定角度的二维图像。因为观察者总是对四维光场中任意一个角度的图像感兴趣，而不仅仅对某些固定角度的图像，评价光场图像角度上连续的质量比仅仅评价少数固定角度的光场质量更为重要。由于实际应用中，光场采集设备只能记录离散的光场信息，且受限于工艺水平，一般而言对于实际的光场数据，uv平面的采样点（视点）分辨率远远小于xy平面二维图像的空间分辨率，因此进行光场渲染并进行全光场的评价是有必要的。

光场的渲染虚拟视点可以理解为通过采样与插值合成的uv平面上任意实数坐标的合成子孔径图，当视点在uv平面上自由移动时，光场的渲染可通过一个四线性插值得到，又因为前述的原因，采样点分辨率远远小于二维切片图像的空间分辨率，因此出于简化复杂度的考虑，假设插值后的光场子孔径图像素的位置与插值前相同，此插值可简化为一个双线性插值[2]。插值中，合成子孔径图P(u+Δu,v+Δv,x,y)可通过其相邻的最近4个视点的子孔径图重采样得到。

其中，P(u,v,x,y)、P(u+1,v,x,y)、P(u,v+1,x,y)、P(u+1,v+1,x,y)分别为距离待求合成子孔径图最近的4个实际存在的视点，Δu，Δv∈[0,1]为实数。图2为采用双线性插值，利用最近邻的4条实际存在的光线重采样得到的虚拟光线，其中蓝线所示为最近邻的4条实际存在的光线，红线所示为重采样得到的虚拟光线。

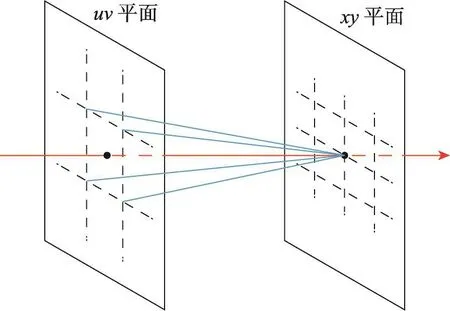
Fig.2 Using bilinear interpolation to obtain virtual light ray图2 采用双线性插值得到虚拟光线

由于像素亮度值被建模为独立的正态随机变量，根据正态随机变量的性质，渲染生成的虚拟子孔径图中的任意像素p(u+Δu,v+Δv,x,y)也应服从正态分布，可表示为：

其中，此分布的均值Yp与方差分别计算如下：

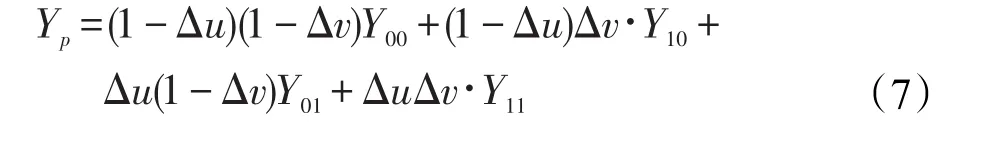
对任意4张相邻子孔径图使用双线性插值可以渲染出uv平面上任意位置连续合成的子孔径图。并且渲染子孔径图中的任意像素均被建模为基于置信度的随机分布，通过衡量编解码前后对应像素随机分布的差异，即可对编码损失进行评价。

3.3 计算KL散度及其对数表示

如前文所述，在编码过程中已被建模为随机变量的像素亮度的均值会发生偏移，因此可引入KL散度（又名相对熵）[6]来量化计算每一个像素点因编码导致的偏移的幅度。KL散度能度量一个随机分布与另一个随机分布的距离，设有两个独立正态分布，其KL散度DKL(p||q)计算如下：

结合前述的像素随机模型，对任意像素p(k+x,l+y,i,j)及其对应的解码后像素p′(k+x,l+y,i,j)，两者之间的KL散度可重写为：

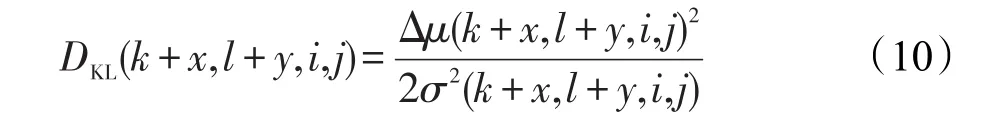
其中，k、l为正整数，代表子孔径图在uv平面上的坐标，x,y∈[0,1]；i、j也为正整数，代表像素在子孔径图中的坐标；Δμ(k+x,l+y,i,j)为像素点p与p′的均值之差；σ(k+x,l+y,i,j)=σp=σp′代表像素点p与p′的标准差，其值可由式（3）计算得到。可以看到，虽然一般来说KL散度为非对称指标而不常用于图像的客观评价之中，然而在本指标模型中，如式（10）所示两个像素点之间的KL散度为对称形式，因此在本模型中引入KL散度作为量化指标是合理的。

由式（3）与式（10）可推得，假设编码带来的偏移一定（反映在编码前后对应像素的均值偏移一定），当像素的置信度增加时，像素随机模型的标准差将降低，相应的KL散度DKL也将增加。由于KL散度DKL用以度量光场编码中的信息损失，DKL越大，信息损失越多，因此可推论得到，光场图像中置信度愈高的区域在编码后的损失愈大。

对任意实数位置的像素KL散度进行积分求和可得：

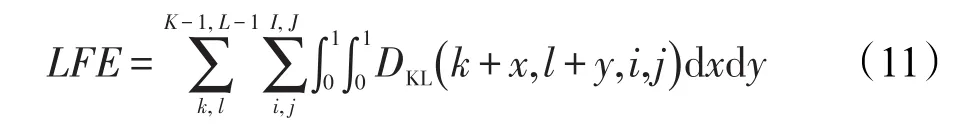
其中，K×L×I×J为光场图片的分辨率；K×L为uv平面视点的数量，即子孔径图的数量；I×J为xy平面上子孔径图的分辨率。累积的KL散度（记为LFE）代表由光学畸变以及压缩损失带来的总共的误差，将LFE称之为光场熵，即本文所提出用于光场编码客观评价的新指标。区别于传统图像指标如PSNR，该新指标直接对四维结构的光场图像整体的压缩损失进行了度量，而不仅仅对光场图像的子集，也就是一系列二维图像切片进行度量；同时还将光场捕捉中的特有畸变纳入指标模型，因此从理论上能更好地反映光场压缩后的质量。

由于LFE为累积值，其量级较大而较不直观，因此可参考PSNR的定义将光场熵以对数形式表示，对数形式的光场熵记为pLFE，计算如下：

其中，σmin由式（4）给出。经过式（12）与式（13），光场图片的光场熵可一一转换为如PSNR一般的对数形式。

4 光场编码质量评价

4.1 客观评价实验

本节将提出的新指标光场熵与传统指标PSNR分别应用于数种前沿的伪时间序列光场编码算法，并进行比较分析。

根据文献[4]的方法，定义一张光场图片的PSNR如下：

PSNRY(k,l)为一张子孔径图的PSNR。

MSE(k,l)为一张子孔径图的均方误差。

i、j为一张子孔径图中任意像素在xy平面上的坐标；I×J为子孔径图像素数量；Y(i,j)、Y′(i,j)为像素点及其解码后像素点的亮度值。

4.1.1 实验数据准备与编码条件

本次光场编码实验采用一个经典的公开光场图片数据集[15]，此数据集采用LytroIllum相机拍摄而得，总共4张光场图片被选择以代表数种不同的场景，此4 张图片名称分别为“ceiling_light”“poppies”“rusty_handle”“sophie_and_vincent”，代表“包含自然光或人造光的图像”“广角下的风景”“近距离自然场景”“中度景深下的人像”这4种具有典型性的光场图像。为了表述方便，以下按照同样的顺序将这4张光场图片记为I01～I04。原始的光场图像经过MATLABLF工具包[16-17]处理为四维光场的格式待用。

4种经典的伪时间序列光场压缩算法被选中作为指标性能对比的材料。需要一提的是，本文新提出指标的使用并不限于此种光场编码方法。

4 种编码方法分别名为“zig-zag”“snake”“diagonal”“spiral”，其序列扫描顺序的示意图如图3所示。

经过4种扫描顺序形成伪时间序列后，使用HEVC标准视频编码器对4种伪时间序列进行编解码，视频编码使用固定QP参数，一共4种固定的QP（22、27、32、37）被选中以生成不同压缩率的码流，码流的比特率计算如下（码流文件大小单位bit,比特率单位bpp）：

本实验中选用的光场图像具有相同大小的原始光场图片像素，其具体数量为5 368×7 728。转换为四维光场后的四维分辨率为15×15×432×624（前两者为角分辨率，后两者为空间分辨率，即子图像素大小）。

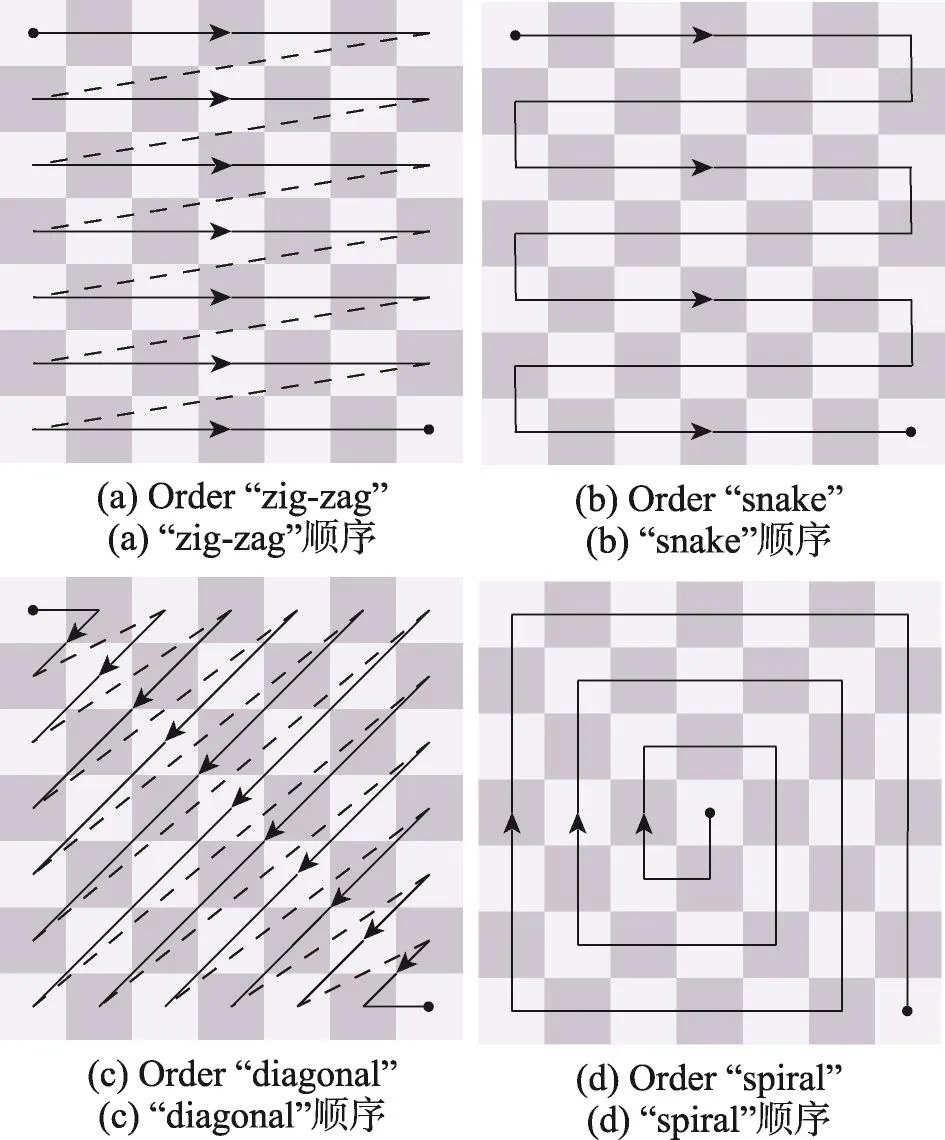
Fig.3 4 scan orders图3 4种扫描顺序

因此，对每一幅光场图片，均有4×4=16种编码条件（4种扫描顺序，4种压缩率）。

4.1.2 实验结果

对编解码前后的光场图像子孔径图分别应用光场熵与PSNR的计算公式，实验的结果如图4所示，可以直观地看到，在两种指标体系下，扫描顺序“spiral”均为性能最优，但针对余下3种编码方法，两种指标则给出了不同的评价。

4.1.3 客观评价分析

为了更好地理解前述光场编码客观评价的结果，引入BDrate（Bjontegaard-Delta率）[18]作为量化评价指标，以衡量两种编码算法性能的优劣。BDrate衡量不同编码方法达到同样质量时所耗费的bit的差异，其值为百分数。为正，则代表考察算法比基准算法多消耗bit的相对比例；为负，则代表节约的bit的相对比例。BDrate默认使用PSNR进行计算，但显然可以用pLFE进行替代计算。

以“spiral”为基准编码方法，完整的客观实验评价结果见表1与表2所示。

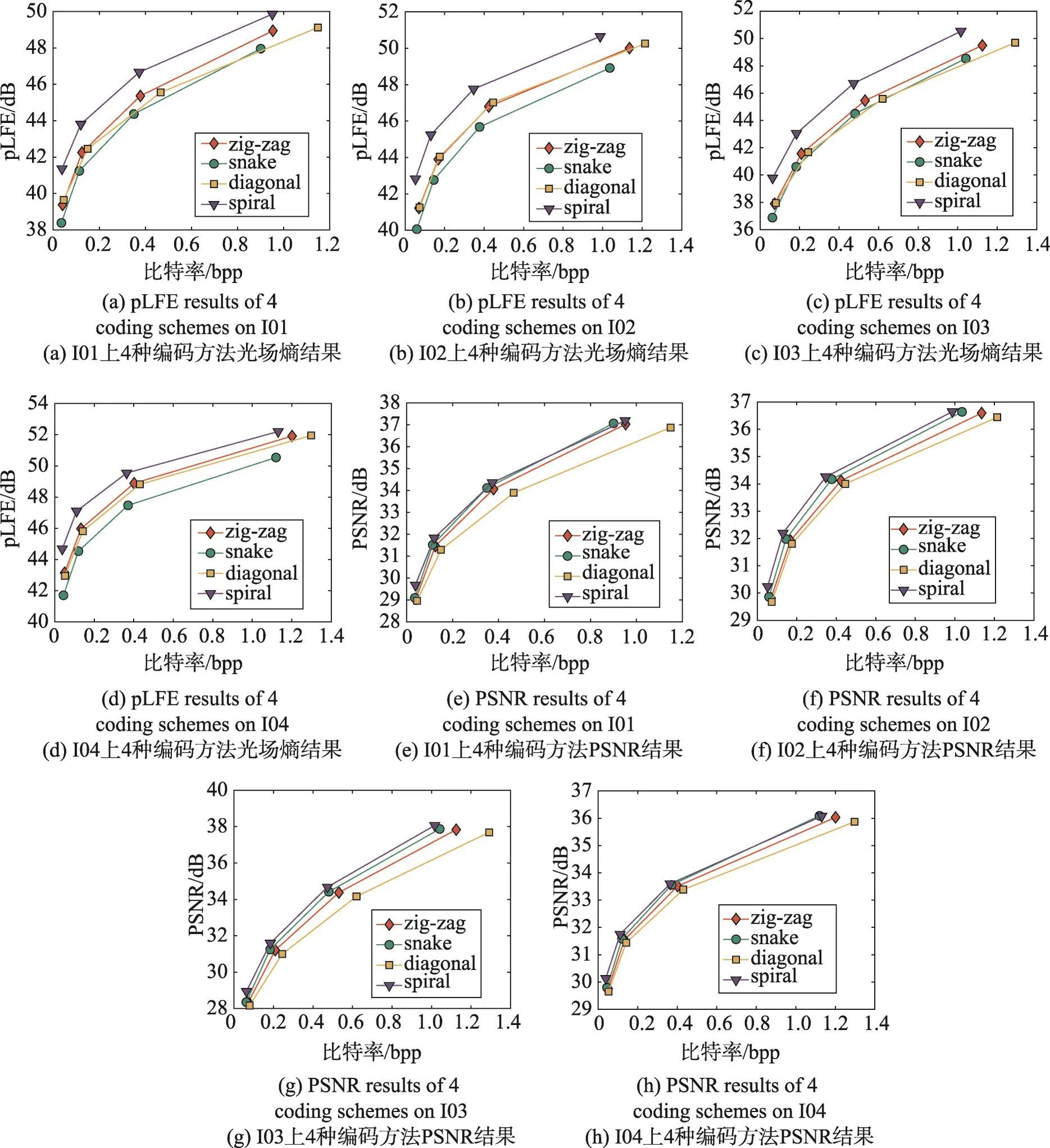
Fig.4 Illustrations of proposed pLFE and PSNR of 4 light field images with 4 different bpps图4 4种比特率下4种编码方法pLFE与PSNR示意图

从表1与表2中的结果可以看出，pLFE指标体系下，4种光场编码性能从优到劣的排名为“spiral”“zigzag”“diagonal”“snake”，而在PSNR指标体系下，4种编码的排名为“spiral”“snake”“zig-zag”“diagonal”。

客观评价实验的结果在两种指标下产生了差异，差异的根源在于两种客观指标设计时的不同考量；新指标将光场光学畸变与角空间连续性纳入了考量，因此展现出了与传统指标不一样的特点。然而客观指标的评价性能，需要以其与人眼主观感受的相关性进行验证。下一节将介绍主观测试方法以对两种不同的客观指标的性能进行对比分析。

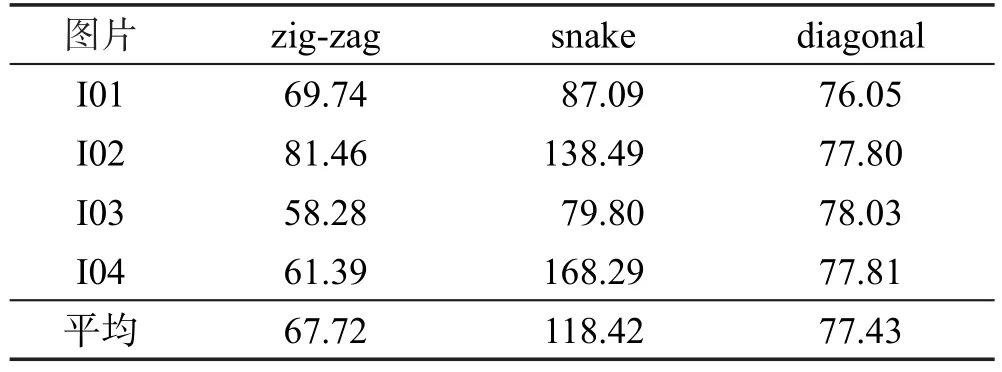
Table 1 Evaluation results of 4 coding schemes using pLFE表1 使用pLFE对4种编码方法的评价结果 %

Table 2 Evaluation results of 4 coding schemes using PSNR表2 使用PSNR对4种编码方法的评价结果 %

4.2 主观测试与指标性能分析

4.2.1 主观测试方法

在图像编码领域，客观指标评价往往与人眼的主观感受存在差距，因此在评价光场编码的性能时，主观测试总是不容忽视。

本节针对前文所述的光场图片以及编码条件，采用双激励损伤量表的被动测试方法，对4种光场编码方法进行了人眼的主观测试。

本测试方法中，受试者将观看总共128段已事先编辑好的视频。测试者总是先观看未经编码的子孔径图组成的伪时间序列，再以同样的顺序观看此光场图片经过某种编码条件编解码后的以同样顺序子孔径图组成的伪时间序列。此顺序由经验选定，对4张光场图片的每种编码条件均保持不变。受试者每观看一对视频后立刻做出评分，评分从1到5，1分表示此编码后的光场较未编码的光场图片质量最差，5分表示质量最好，最接近未编码的状态。因为4张光场图片均有16种编码条件，因此受试者一共将做出64次打分。

值得一提的是，受试者均在同样的环境中观看视频，并严格排除了自然光变化的影响，以最大程度反映人眼对光场编码损失的判断。

4.2.2 测试结果处理

一共11名受试者参与了本次测试，受试者的年龄均为18～25岁的范围，其中2名受试者为女性，9名为男性。对11名测试者的结果取平均值，可以得到每张光场图片的每种编码条件下的主观平均分MS。以两种不同的指标pLFE与PSNR作为预测变量，对平均分进行线性拟合，其结果如图5所示。可以看到两种指标均在一定程度上反映了人眼对光场编码质量的主观感受。

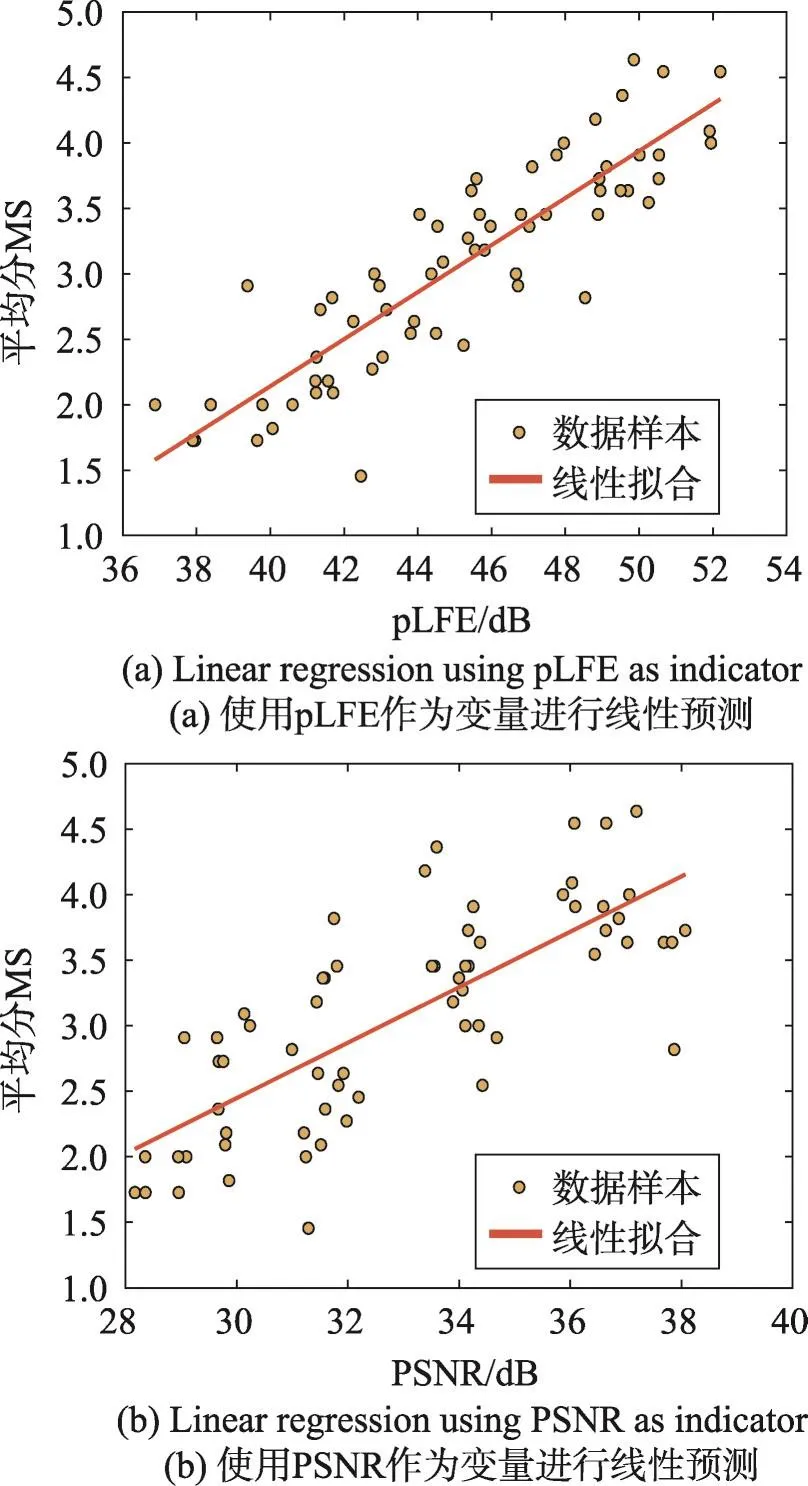
Fig.5 Linear regression analysis图5 线性拟合分析

4.2.3 指标性能分析

如表3所示，经过完整的光场编码质量评价实验之后，可计算得到不同编码条件下的客观评价指标值与人眼主观平均评分的相关性。本文采用统计学中一种经典相关系数——Spearman相关系数来衡量客观指标与主观评分的相关性，本文所提出新指标光场熵在预测人眼主观感受上的性能以0.901 3的相关系数优于PSNR（0.757 5）。主观测试的结果说明了，本文新指标模型设计中的诸多针对光场图像特点改进，在选定的数据集上预测主观感受的性能要强于传统指标PSNR。