落实核心素养的习题教学：过程、模型和思维——以鲁科版必修二“圆周运动”章节为例

江 翔 王玉辉

（永安市第一中学，福建 永安 3660 0 0）

物理习题教学是物理教学的重要环节之一，也是落实学生“物理观念”“科学思维”“科学探究”“科学态度与责任”等核心素养的重要途径。传统习题教学“重结论、轻过程”“重知识、轻方法”“重解析、轻探究”［1］，导致学生主动性不够，缺少内在思维和知识方法发现探究的过程，影响习题课的教学效率，使物理课堂教学失去育人的价值。在核心素养导向的习题教学中，将知识情境化是知识活化并转化为素养的必经途径。［2］本文尝试在基于提升核心素养的习题教学中，通过创设情境激发学生主动学习，关注学生知识方法和技能获取的过程，让学生亲历物理规律的理解和应用过程，并在此过程中注重培养学生建模的思想，通过变式类比的题型训练，掌握研究实际问题的思想方法，提升解决问题的迁移能力，达到举一反三、触类旁通的目的，从而拓展思维能力。最后通过实验助力建模，培养学生科学探究意识和品质，发展学生的创新思维能力。下面以高一物理“圆周运动”习题教学为例进行阐述。

一、过程情境：激发求知欲和转变“物理观念”

实际生活是学生学习的最好情境，教学应与现实生活连接，创设来源于生活实践的物理习题，让学生在实践中学习并养成解决实际问题的能力。

（一）水平面上圆周运动：汽车转弯

水平转台上物块随转盘匀速转动如图1和汽车转弯如图2，这类水平面的圆周运动问题，可以选择汽车转弯的习题情境来分析和训练。

例1：《今日说法》专栏曾报道了在长沙某公路上连续发生了八次大卡车侧翻的的交通事故，在陈先生家门口公路转弯处外侧，现场示意图如图2所示，人们提出了整改建议来防止事故再次发生，下列建议合理的是（ ）。

图1

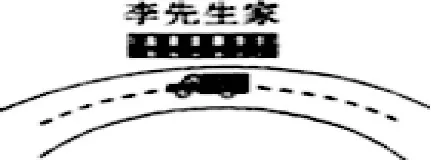
图2

A.转弯处设立限载标志，要求降低车载物品的重量

B.增大车轮与路面间的摩擦

C.转弯处设立限速牌，提示司机不要超速转弯

D.设计弯道路面外高内低

通过选择这道联系生活的汽车转弯习题，学生的兴趣和思考被激发，学生乐于探究转弯向心力来源的分析及安全转弯的速度计算，提出改变路面间摩擦、设立限速标志及改造弯道路面设计如图3的合理建议，从而达到学以致用的目的。

图3

（二）竖直面上圆周运动：汽车过拱形桥和凹形桥

教师：播放①播放汽车慢速行驶安全通过拱形桥；②汽车快速通过拱形桥顶点时水平飞出桥面。

例2：一段圆弧半径为R=10m的拱形桥顶部，如图4(a)，小汽车行驶到桥顶时的速度为v（g取10m/s2），以下说法不正确的是（ ）。

A.当v=10m/s时，重力等于车对桥面的压力

B.无论速度多大，重力有可能小于车对桥面的压力

C.当v=12m/s时，车不能安全通过拱形桥

D.当v=5m/s时，车对桥面的压力是重力的0.75倍

通过播放联系生活的汽车过拱形桥视频并渗透安全教育，其中脱离桥面的视频给学生以震憾，说明汽车过拱桥要有一定安全速度，激发了学生求知欲，习题中选项问题可通过式子来分析，并得出N=0时是汽车安全通过拱形桥的临界。再将习题拓展到凹桥情境如图4(b)，由得出汽车N＞mg，汽车处于超重状态，当汽车速度越大时，桥面给轮胎作用力N就越大，轮胎就有可能爆胎，从而体会到物理学习的现实意义和价值。

二、类比模型：促进知识内化和提升“科学思维”

习题教学可以采用变式来创新习题情境，教师通过对题目的适当引申、变式、拓展，引导学生应对不断变换的习题情境，使学生的知识结构变得系统化，善于归纳形异而质同习题的解题规律和方法，拾级而上，将思维逐渐引向深入。

（一）一题多变

以水平转台上物块随转盘匀速转动的习题入手变式，探究物体即将开始滑动时临界条件及角速度等的计算。如图5所示，改变物体受力条件、转动物体个数和质量，从没有绳子牵连到有绳子牵连，由一个物块到多个物块，习题设置由浅入深，层层递进，符合学生认知发展规律，因为学生发现自己再跳一跳就能够到，内驱力促使学生知识内化，提高了学习的效率。

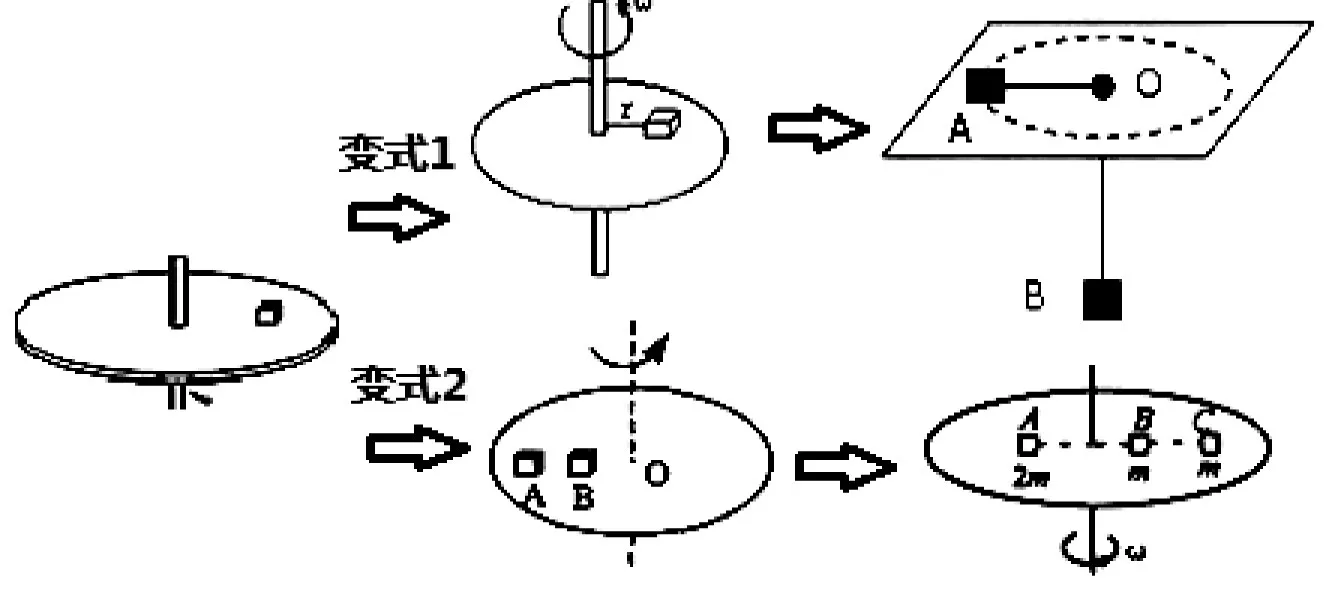
图5

（二）多题归一

以外高内低的路面上汽车转弯问题变式到火车转弯问题，再类比拓展到圆锥摆运动问题，如图6。虽然这些模型的情境不同，但受力情况相同，解答所用的物理规律相同，创设多题归一的变式情境，可以实现触类旁通的教学目的。［3］

图6

还可将圆锥摆模型如图7拓展变式1到两小球的圆锥摆运动，分析两小球线速度和角速度关系等，再变式到游乐场“飞天秋千”的模型，多方位变式情境以内化知识，培养学生良好的思维品质。再创新变式2到小球刚好没有受到圆锥体的支持力，将习题转化为小球在光滑的圆锥面上做圆周运动的临界问题，使研究问题进一步深化。还可把圆锥筒斜面的支持力与绳子的拉力等效，将模型等效为如图7中的“飞车走壁”，相似受力情境的变式，提升学生应用该模型的迁移能力，培养了学生思维的灵活性。

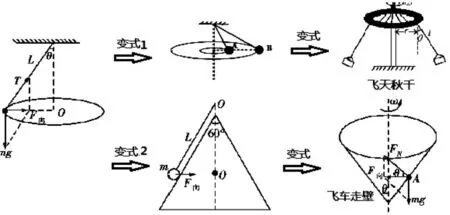
图7

三、实验思维：促进知识建构和养成“科学探究”

习题教学通过创设实验模拟生活情境进行辅助教学，让学生亲自观察，亲身体会，有助于调动学生参与探究的欲望，激活学生的形象思维，帮助理解知识方法，产生更好的学习效果。

例3：游乐场的过山车运行到圆周最高点时，游客头朝下而人不会掉下来（如图8甲）。把它抽象成曲面轨道和圆轨道平滑相连接于B点的模型如图8乙所示。让质量为m的小球从曲面轨道上的C点静止滑下，沿着圆形轨道通过圆周的最高点A，圆轨道的半径为R，CB两点的高度差h=3R，运动过程中摩擦和空气阻力不计，求：①小球通过A时对圆轨道的压力有多大？②试分析在圆周运动的过程中轨道受到小球压力最大在哪个位置？

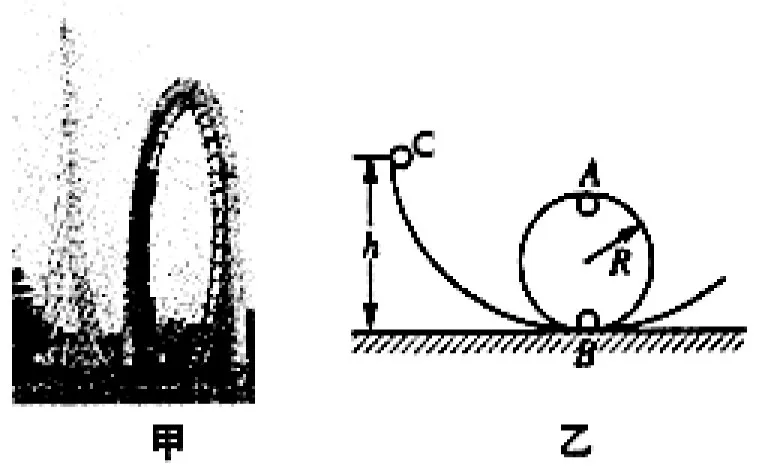
图8

教师：展示例3后，播放一段“过山车”视频后，再实物展示过山车的轨道模型如图9，让小球从斜轨某一高度静止释放，模拟过山车运动。提出问题：从不同高度释放是否影响小球过圆周运动的最高点？并让学生实验。［4］

学生：①学生自行设计几个不同高度（高、中、低）滑下进行实验，发现高度会影响小球过圆周最高点。

②DIS实验：在圆周轨道从B点位置开始每隔45°设置一个压力传感器，记录不同位置处轨道受到小球压力的读数变化。

图9

（一）变抽象为具体，帮助建模

在习题教学中，有些题目的图景比较难建构，导致解题建模受阻，学生借助实物演示有利于建构“过山车”模型是竖直面上圆周运动的“绳模型”如图10，通过创设实验模拟的情境，把抽象的过程更形象地呈现出来，有助于学生感知过程、积极探究，建立“绳模型”后，由牛顿第二定律可得：在最高点A点：mg+和机械能守恒定律可得解出第（1）问。

图10

（二）助力习题结论的验证

第（2）问中问题可以从理论探究和实验探究验证两方面来完成。一是通过机械能守恒定律得vB在整个圆周运动中速度最大和可得在最低点小球对轨道的压力最大。二是轨道的不同位置安装好压力传感器，通过DIS实验，得到一系列压力大小的数据，可以将原本定性的结论变为定量数据，再次验证理论推导的结论，深化规律的理解和应用。

总之，在落实核心素养的习题教学实践中，要树立“过程比结果更重要，模型比题型更重要，思路比套路更重要”的意识，通过创设各种情境，引导学生在解题过程中纠正日常“物理观念”，建立模型，学会“科学思维”和“科学探究”，通过一题多变和多题归一习题训练，能从不断变化的习题情境中找出“不变”的规律方法，形成以不变应万变的高效解题策略，提高了习题教学的有效性，培养学生的探究意识和创新思维能力，从而有利于学生核心素养的提高。