一种新型Ka波段卫星信号抗截获调制方案*

张 喆， 达新宇， 刘慧军

(空军工程大学 信息与导航学院，陕西 西安 710077)

0 引 言

由于军事通信较高的安全需求，Ka波段卫星投入应用，需要一种可靠的抗截获调制方案来保证信号安全传输。当前卫星信号安全传输相关研究主要集中在基于密码学的信号加密与物理层安全方面，其中加权类分数阶傅里叶变换(weighted-type fractional Fourier transform,WFRFT)是一种新型物理层安全手段，具有物理结构简单、信号隐蔽性强的特征，有很大的发展潜力。

文献[1]提出离散WFRFT定义，并论证其构成通信系统的可行性;WFRFT处理后的基带信号星座图分布具有类高斯性，故能起到抗截获功能[2]；梅林通过对WFRFT的误码率分析得出其参数具有抗截获性能；Li T对双层加权类分数阶傅里叶变换(double-layer weighted-type fractional Fourier transform,DL-WFRFT)的基带信号进行研究时，通过观察星座图分布来阐述其抗截获性能[3]；Fang X J将多参数加权类分数阶傅里叶变换(multi-parameters weighted-type fractional Fourier transform,MP-WFRFT)性能与传统方法进行比较时亦使用了基带信号的星座图[4]。综上所述，目前对WFRFT抗截获性能的研究仅停留在未加载波的基带信号星座图上，对加载波后的调制波形未进行研究，且当前研究中有关抗截获性的证明停留在定性分析阶段，并未提出实际的定量评价指标。

针对上述问题，本文提出一种应用在Ka波段卫星上的WFRFT抗截获调制方案。对通信过程中基带信号及调制信号波形特征展开研究,引入互相关系数概念， 研究WFRFT处理前后的调制信号波形的相关程度，建立抗截获性能的具体评价指标。

1 正交相移键控—WFRFT抗截获信号研究

1.1 正交相移键控信号基础

正交相移键控(quadrature phase shift keying,QPSK)信号波形的调制过程为：首先,数据源在基带上进行映射，将得到的结果分为实部与虚部两部分，并分别作为同向/正交(in-phase/ quadrature,I/Q)2路的幅度信息；对2路信号加载波，合成最终的信号波形。QPSK映射关系如表1所示。

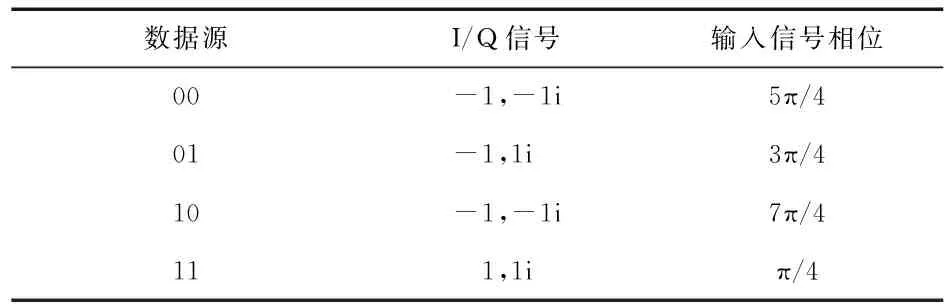
表1 QPSK映射关系

以1 kHz进行采样的传统QPSK调制波形序列s(n)的数学表达式为

s(n)=I(d(n))·cos(2πfcn)+Q(d(n))·

sin(2πfcn

(1)

式中 I(·)为取实部运算,Q(·)为取虚部运算,d(n)为按表1规律映射后得到的基带信号,fc为载波频率。

1.2 QPSK-WFRFT抗截获信号研究

由表1可知，I，Q两路信号中仅存1与-1共2种幅度，得到的最终信号波形具有较强的规律性，易被第三方截获。为使信号具有抗截获性，本文对传统QPSK调制方式进行改进，在信号基带部分加入WFRFT处理，新的调制过程如图1所示。

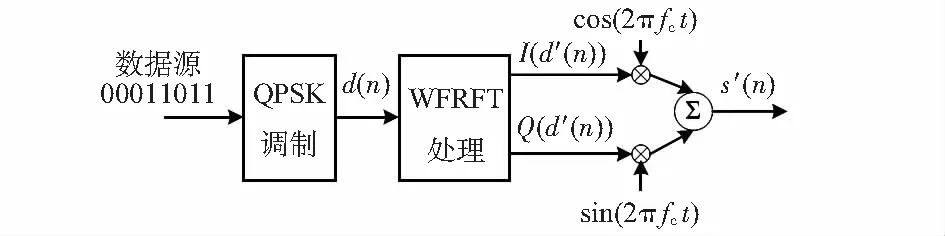
图1 QPSK-WFRFT调制过程

其中，WFRFT处理模块的结构如图2，信号d(n)通过1次离散傅里叶变换(discrete Fourier transform,DFT)和 2次反转后分别与加权系数wl(l=0,1,2,3)相乘，各项相加后得到最终信号输出。

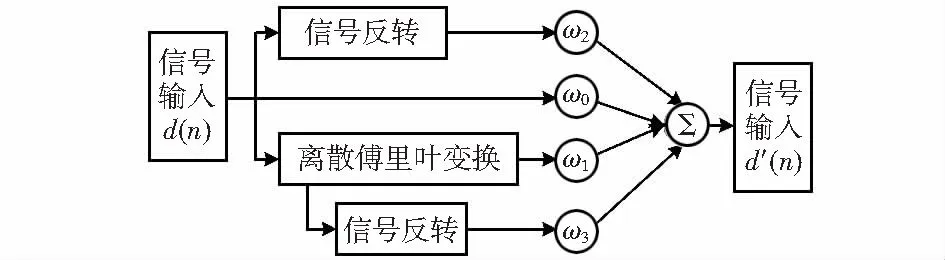
图2 WFRFT处理模块结构

离散WFRFT的数学表达式为[5]

d′(n)=w0(α,V)d(n)+w1(α,V)D(k)+

w2(α,V)d(-n)+w3(α,V)D(-k)

(2)

式中wl(α,V)(l=0,1,2,3)为WFRFT的变化阶数；α为WFRFT的变换阶数，可在[0,4]范围内任意取值；V为尺度向量，取值为任意整数，由Mk=[m0,m1,m2,m3]与Nk=[n0,n1,n2,n3]组成;D(n)为d(n)的归一化DFT，DFT变换对的表达形式为

(3)

wl(α,V)还可进一步表示为[6]

(4)

由式(2)、式(1)，得到QPSK-WFRFT调制信号为

s′(n)=I[w0(α,V)d(n)+w1(α,V)D(n)+

w2(α,V)d(-n)+w3(α,V)D(-n)]·cos(2πfcn)+

Q[w0(α,V)d(n)+w1(α,V)D(n)+w2(α,V)d(-n)+

w3(α,V)D(-n)]·sin(2πfcn)

(5)

式中 当加权系数wl(α,V)中α≠0时，基带信号与调制波形受其影响会发生改变，改变的程度取决于参数α与V的取值，其中，α造成相位的旋转与混淆，V对混淆程度存在微小的影响[7]。本文忽略V造成的影响，令V=0，则最终的波形序列为

s′(n)=I[w0(α)d(n)+w1(α)D(n)+w2(α)d(-n)+

w3(α)D(-n)]·cos(2πfct)+Q[w0(α)d(n)+w1(α)D(n)+w2(α)d(-n)+w3(α)D(-n)]·sin(2πfct)

(6)

2 QPSK-WFRFT抗截获信号的波形

2.1 QPSK-WFRFT基带信号

式(2)为QPSK-WFRFT基带信号，式(6)为经变频后的调制信号。两者均受到变换阶数α的影响，由于WFRFT信号特征具有对称性[7]，故本文只研究α=[0,1]的情况，设数据源长度为10 000，当α取0，0.01，0.1，0.5，0.8，1时,分别对基带信号与调制波形进行仿真。为方便观察，截取前100个信号进行分析。发现α=0时，WFRFT未对信号处理，此时，相当于信号只进行了QPSK映射，基带信号的同相分量与正交分量特征无变化。

当α为0.01，0.1时，经WFRFT处理的基带信号，α取值较小时，WFRFT对基带信号特征的改变不明显，处理前后信号特征具有一定相似性，存在被第三方截获的风险。

α分别取0.5，0.8，1时，随着α取值增大，I/Q分量上产生的幅度值增多，变换前后的信号区别增大，第三方截获通信内容的可能性较低。

2.2 QPSK-WFRFT抗截获信号波形仿真

式(6)给出信号在信道中传播的波形，本文以Ka波段卫星为研究对象，信号波特率取100 bps，载波频率fc为23 GHz,分别对α为0，0.01，0.1，0.5，0.8，1的QPSK-WFRFT调制波形进行仿真，结果如图3所示，可以看出α会对最终的发射波形造成影响，不同的α产生的调制波形不同，α值越大，产生的波形与原QPSK调制信号波形区别越明显，第三方通将WFRFT处理前后波形联系起来的可能性越低。

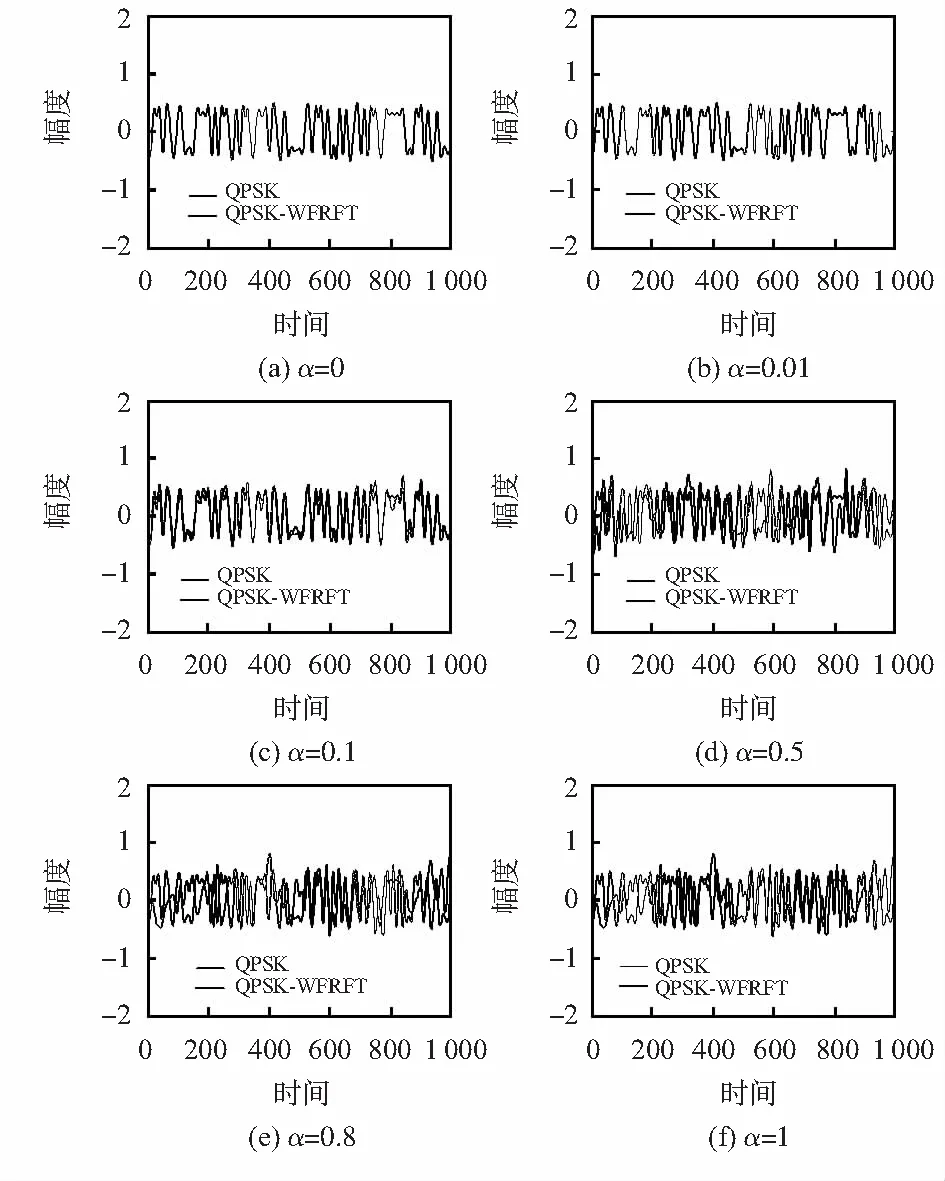
图3 不同α时的QPSK-WFRFT波形

3 QPSK-WFRFT波形抗截获性研究

3.1 QPSK-WFRFT与QPSK波形的互相关性分析

现有WFRFT研究中，主要通过基带信号星座图分布特征定性说明其抗截获性，缺乏定量分析的理论指标。相关系数可以作为一种表征随机变量或信号之间关联程度强弱的统计指标[8～12]。

互相关系数的表达式为

(7)

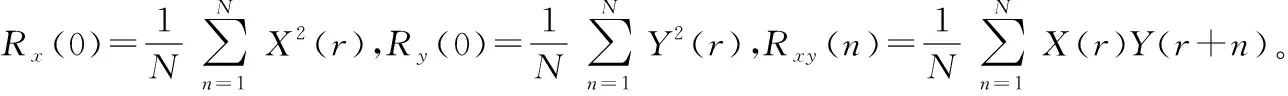
3.2 QPSK-WFRFT波形互相关系数仿真

对载波频率为23 GHz，长度为10 000的QPSK-WFRFT调制信号波形仿真，变换阶数α分别取0，0.01，0.1，0.5，0.8,1，求得到的新波形与QPSK调制信号的互相关系数,相关系数的仿真结果如图4所示。

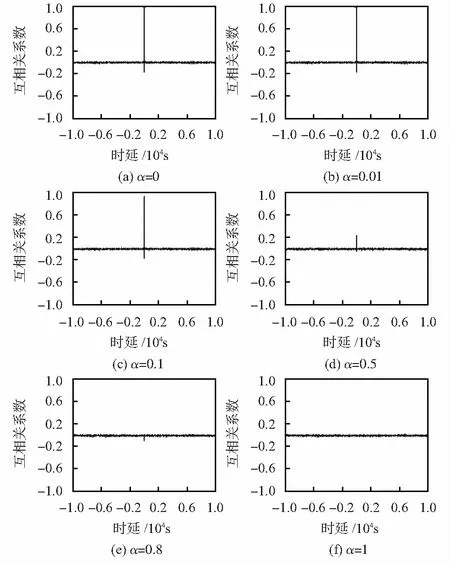
图4 不同α时的QPSK-WFRFT波形互相关系数

对图4进行分析：信号的随机性使得仅在延时为0 s时出现相关峰，该现象表明信号不具有周期性；变换阶数α增大的同时，相关峰数值逐渐减小；当α=0.5时，WFRFT处理前后信号波形的相关峰数值仅为0.247 0，统计学角度上讲，两者之间呈现弱正相关关系，即已无法通过常规手段建立两者之间的联系；而当α=0.8或1时，两者相关峰的取值小于±0.1，几乎不可能与原QPSK的信号波形建立联系，故QPSK-WFRFT调制信号具有抗截获性，且抗截获性能随α增大而增强。

表2给出了对不同参数之间的互相关系数，表中数据表明：对于原QPSK调制信号波形，QPSK-WFRFT采用不同变换阶数α时得到的最大互相关系数不同，随着α值增大，最大相关系数的值减小；两个使用不同α值的QPSK-WFRFT调制信号波形，变换阶数差值越大，相关性越弱，该结论表明，当第三方已知合法用户使用QPSK-WFRFT进行信号调制，截获信号所使用的α与合法用户参数差值过大时，亦无法截获信号。

4 合法用户接收性能分析

对于合法用户，通信质量需要得到保证。假设收发两端完全同步、滤波器对信号的影响忽略不计，对不同变换阶数α、不同信噪比(signal to noise ratio,SNR)条件下的比特误码率(bit error rate,BER)进行仿真分析，其中,α的范围为[0,2]、SNR的范围为[0,12]。

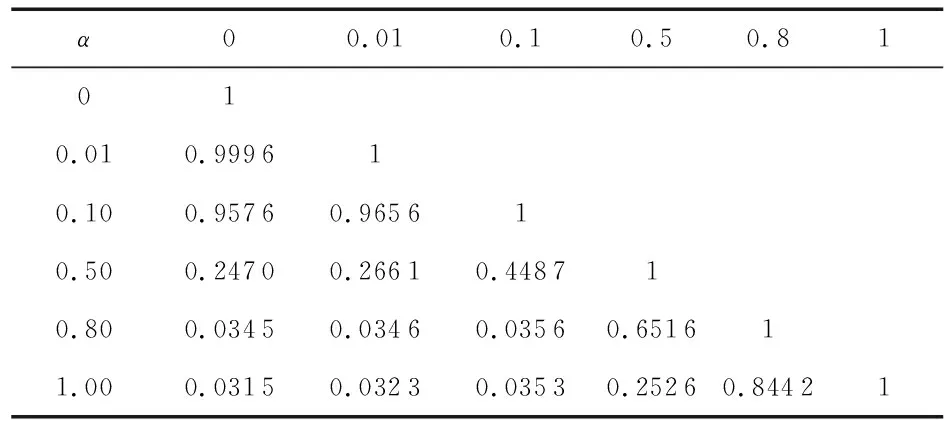
表2 不同变换阶数产生波形的最大互相关系数

图5反映了合法用户α,SNR与BER之间的关系。图中BER的变化趋势表明：合法用户使用不同的α对信号进行调制解调时，系统的BER未受到影响，BER主要受到SNR的影响,且SNR取6.8时，系统BER为1.107×10-2,该数值与QPSK调制信号的理论误码率数值相近，即新方案能够保证通信的可靠性；故QPSK-WFRFT调制方式能够应用在Ka波段卫星通信中。

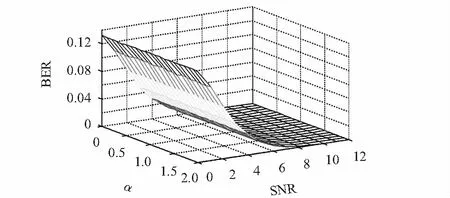
图5 合法用户接收BER，SNR与α的关系

5 结 论

提出将QPSK-WFRFT调制方案应用在Ka波段卫星通信系统当中，研究其基带信号与调制信号波形特征，通过与原信号对比，得出其具有抗截获性的定性结论；引入相关系数概念，通过WFRFT前后信号波形的相关系数定量分析新调制方案的抗截获性能，得到α值越大，第三方截获通信的可能性越小的结论；最后通过对合法用户接的BER分析验证了方案的可行性。

QPSK-WFRFT波形互相关系数仿真结果中，当α=0.8时，相关系数出现峰值为负的情况，对这种情况的理论分析将成为下一步研究的重点，该研究将有助于WFRFT最优化变换阶数的选取。