基于动态启发算子的双种群蚁群算法及其应用*
2018-09-11尹元元游晓明许明乐
尹元元, 游晓明, 许明乐, 刘 升
(1.上海工程技术大学 电子电气工程学院,上海 201600; 2.上海工程技术大学 机械工程学院,上海 201600)
0 引 言
许多智能算法用于解决移动机器人路径规划问题,并取得了很好的效果,其中蚁群优化(ant colony optimization,ACO)算法首先成功解决了旅行商问题[1],其后在组合优化领域得到了广泛应用[2~4]。然而,蚁群算法在解决路径规划问题时存在收敛速度慢、易陷入局部最优解等问题。为了提高算法的收敛速度,唐良等人[5]引入了方向启发,加强搜索限定搜索范围为从起点到终点的椭圆区域。柳长安等人[6]提出了根据目标点自适应函数作为启发因子,加快了算法收敛速度。文献[7]通过建立双蚁群完全交叉算法,解决复杂凹形障碍环境下的机器人路径规划问题,仿真实验结果证明了该算法的有效性。文献[8]引入双种群独立搜索,保证解的多样性的同时,提高算法收敛速度。文献[9]采用两个蚁群分别进行进化求解,并定期交换优良解,增加了解的多样性。
本文算法采用双种群A与B,首先由蚁群A构造一条完整路径,在该路径上随机选取两点作为种群B的起点和终点,重新规划两点之间的路径,并比较两段路径优劣,判断是否进行该段解的替换,并全局更新种群B规划所得路径的信息素。此外,两种群也采用不同的局部信息素挥发系数[10],进行了栅格环境下的机器人路径规划仿真实验[11],结果证明本文算法在收敛速度、避免算法陷入局部最优等方面都具有很好的表现。
1 蚁群系统
蚁群系统(ant conlony system,ACS)2个重要步骤如下:
1)路径建立
在ACS中,蚂蚁从当前节点i选择下一个城市节点j,其状态转移规则为
(1)
式中q为0~1之间的随机数,q0∈(0,1)为可调参数,S为基本蚁群算法的状态转移规则
(2)
式中τij为路径上的信息素浓度;ηij为启发因子;β为能见度启发因子,反映能见度信息的相对重要性;allowedk为蚂蚁下一步可选择的城市节点组合。
2)信息素更新
每只蚂蚁建立一条从起点到终点的路径后,需要对路径上的信息素进行局部更新,当所有蚂蚁完成一次循环后,将对当前所有路径中的最短路径进行全局信息素更新
τij=(1-α)τij+αΔτij
(3)
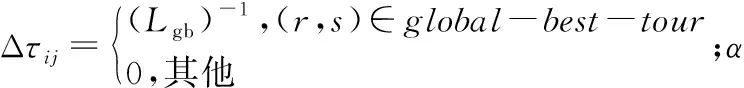
2 改进的ACS
2.1 动态随机启发算子
本文将两种群分为种群A与种群B,其中,种群B中应用动态随机启发算子,其起始点SB和目标点OB在种群A规划所得的路径上随机选取。当种群A完成一次迭代,种群B根据当代最优路径随机选取终点,新的启发函数为
(4)
式中dig为蚂蚁可选择的下个栅格与种群B随机选择的新的终点之间的距离。
2.2 新型双种群
在种群A所得当代最优路径上随机选取两点作为种群B的起点SB和终点GB,且种群B重新规划两点之间的路径:若种群B找到的两点间的最短路径比该段由种群A规划所得路径质量更优,则用种群B规划的最优路径替换种群A的该段路径,并全局更新种群B规划所得路径的信息素;否则,种群B不进行全局信息素更新。
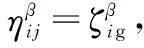
2.3 算法步骤
1)参数初始化,包括:两蚁群规模m1,m2,最大迭代次数K,表征启发式信息重要程度的参数β,信息素蒸发因子ρ,新增信息素强度因子q等。
2)将种群A中m1只蚂蚁置于起始点S。
3)选取种群A的当代最短路径,并在该路径上随机选择两栅格SB,OB。
4)计算两栅格SB与OB之间的路径长度d1。
5)将栅格SB,OB作为种群B的起点和终点,计算所得路径长度d2。
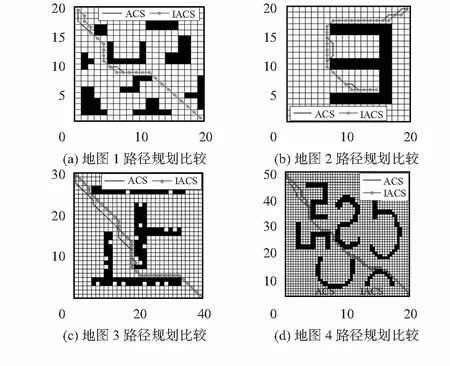
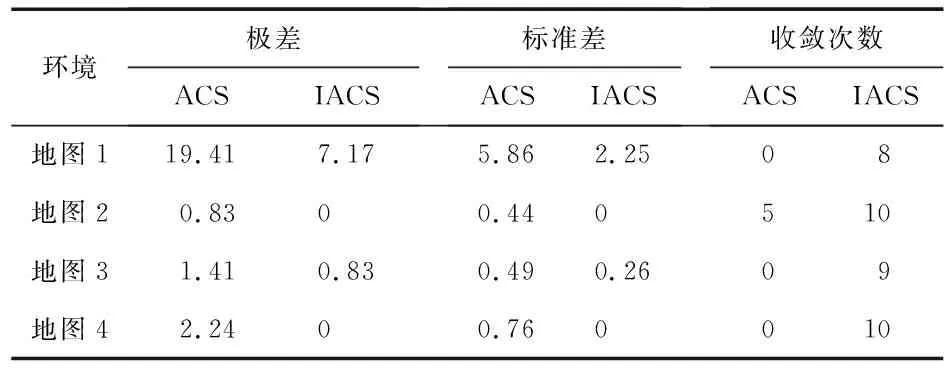
6)若d2 7)若循环次数NC≥NCmax,则算法结束;否则;转到步骤(3)。 为了验证改进算法的有效性,本文分别采用ACS和改进的蚁群系统(improved ACS,IACS)在MATLAB软件平台下进行机器人路径规划仿真实验。图1为2种算法在4种地图下的路径规化对比。 图1 ACS与IACS在4种地图下的仿真实验 由表1、表2的实验结果证明,改进的算法在最短路径和平均路径长度以及路径长度的极差和标准差等方面表现得更好,且与传统ACS相比,IACS算法找到最优路径的次数高很多,平均迭代时间较少,显然,改进后的算法具有更好的规划效率。 表1 ACS与IACS的路径规划仿真实验结果 cm 表2 ACS与IACS的路径规划结果比较 本文介绍了一种改进的双种群蚁群算法,仿真结果表明:该算法能够克服传统ACS算法的缺点,具有较好的路径规划性能。3 仿真分析

4 结束语
