基于自适应随机共振理论的太赫兹雷达信号检测方法∗

王珊 王辅忠

(天津工业大学理学院,天津 300378)

1 引 言

近年来,随着太赫兹技术的发展,太赫兹雷达的研究已经广泛开展[1−3].太赫兹波是指频率波段为0.1—10 THz的电磁波,与微波、毫米波相比,其波长短且带宽大,应用于雷达方面具有无测量盲区、低功率及低截获率等众多优势[4,5].

一般来说,太赫兹雷达的回波信号为带噪信号,因此在差频信号频谱分析过程中,需对其进行去噪检测.目前雷达信号常用的处理方法为快速傅里叶变换法(fast fourier transform,FFT)[6]和滤波法[7−9].直接FFT法由于存在噪声干扰,影响信号频率估计能力.滤波法从消除噪声的角度来检测信号,但降噪的同时也削弱了有用的特征信号,模糊了信号的位置信息,影响太赫兹雷达的检测能力.而随机共振(stochastic resonance,SR)系统能够利用噪声能量,放大弱信号而抑制噪声[10−12].

本文根据差频信号的特点,提出基于自适应随机共振理论的太赫兹雷达信号检测方法.以太赫兹雷达的差频信号为研究对象,采用二次采样算法,通过自适应随机共振系统,进行信号的提取及尺度恢复,自动检测差频信号,提高太赫兹雷达测距能力.

2 太赫兹信号的自适应SR检测理论

2.1 太赫兹雷达测距基本原理

太赫兹线性调频连续雷达系统发射的是经线性调频的连续波,通过分析发出的电磁波与目标反射的回波做混频,从而得到差频信号,通过差频信号的主频来提取距离信息,得出目标的状态.其发射信号公式表示如下[13,14]:

(1)式中A为发射信号的幅度值;f0为起始频率;k是调频斜率,其中k=BW/T.BW为信号带宽,即起始频率的差值;T为脉冲带宽(调频时间).发射信号的最大频率为:fmax=f0+kT=f0+BW.

雷达发射信号辐射出去之后,遇到目标,目标反射回信号.接收信号表达式为

(2)式中,t0=2R/C为延迟时间,R是目标与雷达之间的距离,C是光速.反射信号被接收之后,与接收机的发射信号进行混频,混频会产生两项的和与差.发射信号与接收信号的差值即为差频频率fb,与目标距离成正比.距离值由下式给出:

则延迟时间t0可表达为

混频之后,得到所需要的差频信号,其表达式如下:

由(4)式和(5)式可得差频信号的表达式为

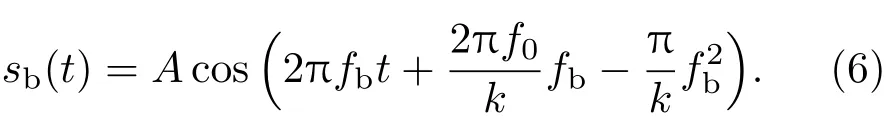
通过对时域差频信号进行FFT之后,可以在频率中找到差频产生的峰值.此频率峰值可以转换成距离值.因此测距系统的关键在于检测差频信号.在带宽B和周期T一定的条件下,得到差频信号fb,便可计算距离R.所以差频信号的检测能力直接影响测距的能力.

由于信号在传播过程中能量损耗,再叠加上空域中其他杂波以及噪声信号,接收机接收到的信号从时域上已经无法辨别出所需要的信息,利用传统的去噪方法,噪声虽然去除了,但同时对于其中的雷达信号也产生了影响,甚至损坏雷达信号,造成分析错误甚至误判,对于测距能力而言是十分不利的.而随机共振的特性决定了它在雷达信号检测方面的广泛应用[15].

2.2 太赫兹信号的随机共振原理

非线性双稳系统的动力学方程可用Langevin方程[16−18]表示:

式中a,b为非线性双稳系数;x(t)是双稳系统输出信号;n(t)是强度为D的加性高斯白噪声;s(t)为待测输入信号.

太赫兹雷达系统发射信号为线性调频连续波,信号在接收和传输过程中信号受到噪声的污染,混频之后,得到待测含噪差频信号表达式为

当差频信号sb(t)和噪声n(t)通过双稳态非线性系统,调节参数a,b,使信号、噪声及非线性系统之间达到匹配,一部分噪声能量将转化到信号身上,从而发生随机共振,提取出被噪声淹没的差频信号,计算出测量距离.

3 太赫兹信号的自适应SR检测系统设计

3.1 自适应SR系统设计

自适应算法公式[19,20]为

式中,SNR为信噪比,SNRm为最大信噪比,Ac为临界幅值,Acmin为最小临界幅值.系统采用最小均方误差法(LMS)确定最小临界幅值,即给定参数a,b的循环步长和先后顺序,每固定一个b值,调节a值,计算系统输出的信噪比并存入矩阵;a循环完毕,计算最大信噪比与其对应的临界幅值,将信噪比与临界幅值分别存入列向量中;b循环时,比较列向量中临界幅值的大小,得到系统最小临界幅值Acmin.系统根据Acmin,采用逆向定位法[21]确定最优参数a1,b1和信噪比SNR1.根据数值相同,确定Acmin在Ac列向量中的位置;根据行位置相同,得到SNRm列向量的数值,即为SNR1;由行位置相同,且满足与SNR1数值相同,确定SNR1在SNR矩阵中的位置;由行列位置均相同,得到a1,b1在ab矩阵中的位置.具体流程如图1所示.

图1 自适应随机共振程序流程图Fig.1.Program tree of adaptive SR system.

图1中a,b为双稳系统的参数;n1,n2分别为参数a,b的循环次数,矩阵形式为(n1,n2);SNR是信噪比,矩阵形式为(n1,n2);SNRm为矩阵SNR的行最大值,矩阵形式为(n2,1)的列向量;Ac是临界幅值,矩阵形式为(n2,1)的列向量.经过自适应系统后,最后系统输出参数a1,b1,SNR1,Acmin.

3.2 太赫兹信号的自适应SR检测流程设计

太赫兹差频信号的频率范围为0.1—10 THz,频率不满足绝热近似条件,无法通过双稳态非线性系统达到随机共振.因此,本文先通过二次采样算法[22−24],将信号的频率范围线性压缩到0—1 Hz,然后再通过自适应随机共振得到最优输出信号,其实现流程如图2所示.

本文对含噪的差频信号进行二次采样,输入自适应随机共振系统中,以最优频谱值作为高信噪比的评价标准,同时结合临界幅值,在满足较大信噪比与较小临界幅值的条件下,采用逆向定位法确定自动获得最优参数,实现最优随机共振.然后将含噪差频信号重新经过自适应随机共振系统,经尺度恢复后实现太赫兹雷达信号的自适应SR检测.

图2 自适应SR太赫兹信号检测流程图Fig.2.Processing chart of terahertz signal detection with adaptive SR system.

4 实验结果与分析

本文在Matlab中进行仿真验证,实验设定相关参数:发射信号为线性调频连续波s0(t)=Acos(2πf0t+πkt2),其中信号幅度A=0.3 V[25],初始频率f0=10 GHz,周期为T=2×10−5s,带宽BW=3 GHz.含噪差频信号为S(t)=sb(t)+n(t),其中噪声强度D=2 V.设定采样频率fs1=5×107Hz,二次采样频率fs2=5 Hz,最优系统参数参数范围a(0,0.5),b(0,0.5),自适应系统的循环步长U1=0.002,U2=0.002.

取测量距离R=1000 mm处的差频信号,其理论对应的差频信号频率fb=1×105Hz.将含噪差频信号输入自适应随机共振系统,得到最优参数a=0.002,b=0.012.含噪差频信号与其经过自适应SR系统的频谱图如图3(a)与图3(b)所示.

对比图3(a)与图3(b)的波形,图3(a)波形振荡较图3(b)剧烈,波形存在许多高频小毛刺,待测的差频信号频谱值很低.而经过自适应随机共振系统后,噪声能量向差频信号发生了转移,差频信号能量被增强,质量得到很大改善,初始频谱值由110.1上升到7172,提高了64.1倍.整个系统的初始信噪比由−11.94 dB提高到−0.179 dB,信噪比增益为11.761 dB,表明太赫兹雷达信号的检测能力得到提升.

图3 (a)含噪差频信号的时域图、频域图与二次采样频域图;(b)含噪差频信号经过自适应SR系统的时域图、频域图与尺度恢复频域图Fig.3.(a)The time domain graph and the spectrum chart of the noised different-frequency signal and it’s twice sampling spectrum chart;(b)the time domain graph and the spectrum chart of the noised differentfrequency and it’s scale recovery spectrum chart after the adaptive SR system.

取测距范围R为1—9 m之间的9个测量点.设定采样频率fs1=5×107Hz,二次采样频率fs2=5 Hz.将含噪差频信号输入自适应随机共振系统,得到距离测距能力如表1所列.

表1显示了经过自适应随机共振系统后,太赫兹雷达系统的差频信号在不同距离上的信噪比与信噪比增益.在9个测量点上,随着测量距离的减小,差频信号频率随之减小,经过自适应随机共振系统后信号信噪比增大,信噪比增益同步增大,其中测量距离R=1000 mm时信噪比增益最大,为11.761 dB.由此可见,本文方法提高了太赫兹雷达的测距能力,平均信噪比增益为9.684 dB.

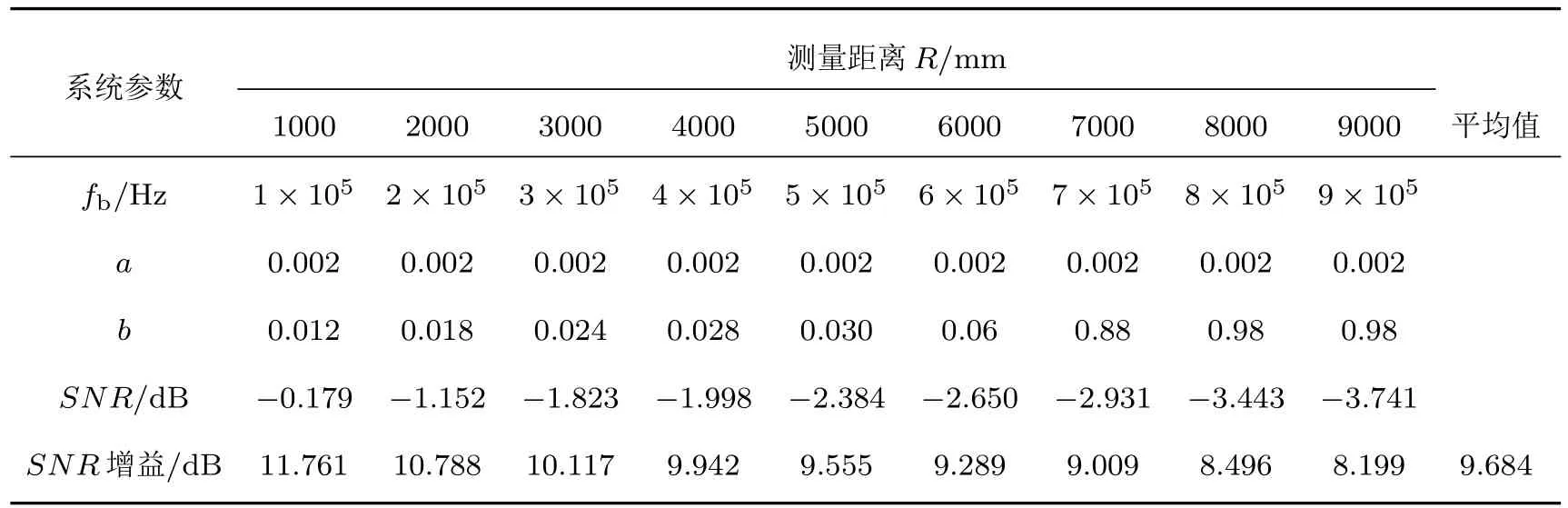
表1 差频信号在不同距离处的测量对比Table 1.Comparison of the different-frequency signal’s details at different measuring distance.

图4 三种方法在不同距离上的信噪比Fig.4.The output SNR graph of three methods at different measuring distances.

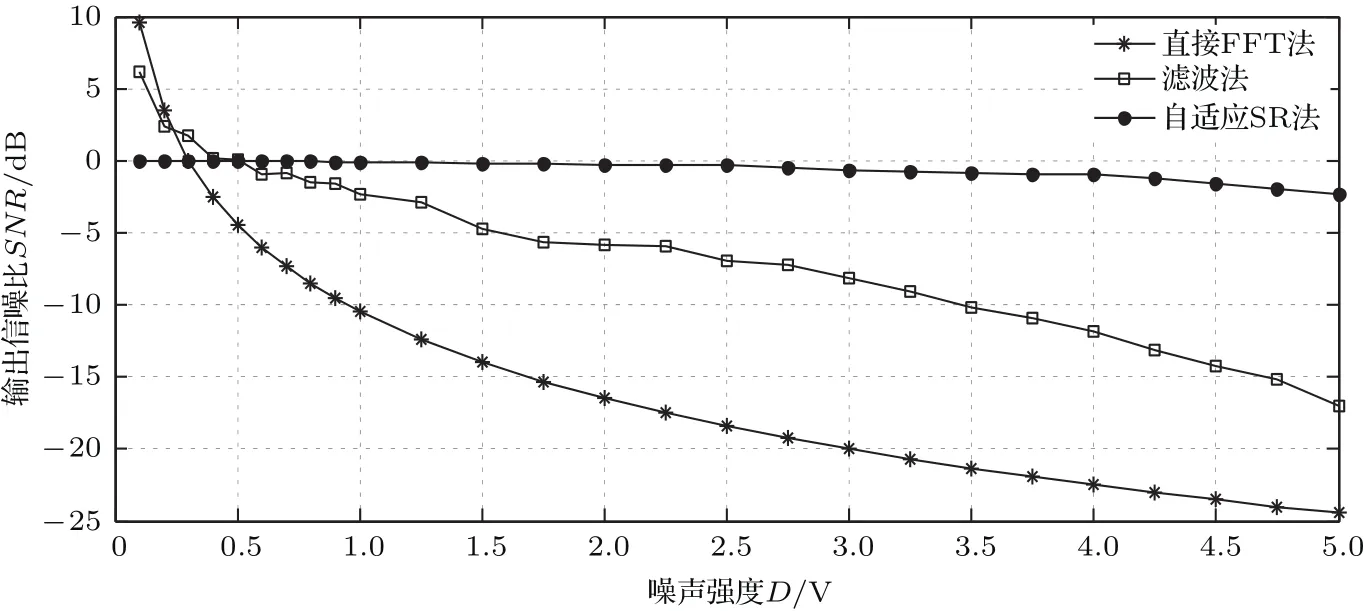
图5 三种方法在不同强度噪声下的输出信噪比Fig.5.The output SNR graph of three methods under different intensity noise.

图4为不同的测量距离时,分别采用直接FFT方法、滤波方法和自适应随机共振模型的输出信噪比对比图.对不同的测量距离,本文方法的输出信噪比均优于直接FFT法和滤波法,其中在R=1000 mm处滤波法的信噪比增益为6.485 dB,采用本文方法信噪比增益为11.061 dB,信噪比增益最大提高了70.56%.表明对不同测量距离,相对于传统方法,含噪太赫兹差频信号经过本文所提系统得到了更好的恢复.

图5为在不同的噪声强度背景下,分别采用直接FFT法、滤波法和自适应随机共振模型的输出信噪比曲线.从图5中可以看出系统的输出信噪比随着输入噪声强度的增加而减小.系统输入的噪声强度在0.5—1 V之间时,自适应SR系统输出的信噪比大于传统滤波系统的输出信噪比,但增益幅度不大,最大信噪比增益为2.148 dB.系统输入的噪声强度在1—5 V之间时,自适应SR系统输出的信噪比明显大于滤波系统,在D=5 V处信噪比增益最大,为14.018 dB.同时,采用自适应SR系统输出的信噪比曲线下降幅度趋于平滑,曲率为0.507,而滤波模型的信噪比曲率为3.765,降低了86.5%.此结果表明在强噪声背景下,利用自适应随机共振方法提取太赫兹信号获得信息的能力优于传统方法.

5 结 论

本文提出了一种基于自适应随机共振理论的太赫兹雷达信号检测方法,提高了太赫兹雷达系统的测距能力.对含有噪声的太赫兹差频信号进行二次采样后输入自适应随机共振系统,经优化自动得到最优参数进行信号的提取,对输出信号进行尺度恢复,从噪声中提取出有用的差频信号.实验仿真表明:经过自适应随机共振系统后,测量距离为1000 mm处,差频信号初始频谱值提高了64.1倍,系统信噪比增益为11.761 dB;不同测量距离时,输出信噪比的平均增益为9.6843 dB,相对于滤波法,在测量距离为1000 mm处信噪比增益最大,提高了70.56%;输入噪声强度为1—5 V之间时,自适应SR系统输出信噪比大于传统方法的输出信噪比,输出信噪比曲线的曲率低于滤波法,降低了86.5%,其中噪声强度为5 V时信噪比增益最大,为14.018 dB.本文所提方法不但解决了差频信号中噪声对于信号的覆盖问题,而且利用共振时噪声能量向信号转移的特性,提高太赫兹差频信号系统的输出信噪比,有利于后续信号进一步处理.相对于传统方法,该系统能更有效地实现噪声中对太赫兹差频信号的提取,具有十分广阔的应用前景.