能够突破标准量子极限的原子双数态的制备研究∗
2018-09-11郑盟锟1尤力1
郑盟锟1)2)† 尤力1)2)‡
1)(清华大学物理系,低维量子物理国家重点实验室,北京 100084)
2)(量子物质科学协同创新中心,北京 100084)
1 引 言
目前世界上最精密的物理量测量(包括时频标准和引力波的探测)大多是通过干涉实验完成的.例如激光干涉引力波天文台(LIGO)就是一个臂长4 km的光学腔增强Michelson光学干涉仪[1].而所谓的原子钟则是利用原子内态干涉测量其量子波函数的时间相位来修正电磁波(时钟)频率的一种科学装置.一个双模干涉仪的基本工作原理如下:用于探测某物理量的信息载体粒子相干地处于两条路径或内态的叠加态,两条路径的相对光程变化或者内态的相对时间相位受到待测物理量的影响而改变,这个相位差θ可以通过将两条路径(内态)合束干涉而测定.干涉实验的一个重要考量是在有限的测量资源(例如时间和总粒子数)下实现尽可能小的相位测量不确定度∆θ.后者由技术(经典的)和基础(量子的)噪声决定.在一个理想的、不存在技术噪声的双路径干涉仪中,如果参与干涉测量的N个粒子之间没有关联或者只具备经典的关联,那么相位测量的不确定度最终将受限于所谓的经典极限,也叫作标准量子极限(standard quantum limit,SQL).LIGO和世界上最先进的原子钟的测量不确定度目前都已经逼近这一极限.那么,为什么不通过简单增加参与干涉实验的粒子数来提高测量精度呢?一般而言,所有实验资源都是有限的,总会存在某种技术原因限制了参与干涉的粒子数.例如,在LIGO的实验中,参与干涉的光子数目主要受限于光学腔的反射镜镀膜的光强承受能力.而在原子钟实验中,由于原子间的碰撞会改变能级的跃迁频率,原子过多带来的碰撞效应反而会降低原子钟的准确度.
幸运的是,标准量子极限并不是量子物理允许的终极极限.量子计量研究的一个重要方向就是探索如何利用量子资源,例如量子纠缠或量子噪声压缩等,来实现超越经典极限的测量精度.反过来,基于量子关联的量子计量研究又能加深我们对多粒子量子纠缠态基本性质的理解.特别是对超越标准量子极限研究有价值的量子态一般由几千个甚至上百万个粒子组成,想要对每个粒子的量子态进行独立的操控和探测,并由此获得包含所有粒子信息的完整量子波函数的想法是不现实的.在量子计量实验中,人们往往只关注对所有粒子等同的集体调控和测量.在这种情况下,如何利用有限的集体测量结果表征一个多体系统的纠缠性质变成了一个很重要的问题,这也是量子计量领域的重要研究内容.
可实现超越经典极限测量精度的量子纠缠态包括自旋压缩态[2−10],NOON态[11−13],Greenberger-Horne-Zeilinger(GHZ)态和Dicke态[14−19]等.可实现上述纠缠态的粒子包括了利用自发参量下转换生成的纠缠光子、基于离子阱调控探测技术的离子、基于光学腔量子非破坏测量的原子和基于带自旋分量的玻色-爱因斯坦凝聚体(BEC)的超冷原子等.所涉及的领域和内容十分广泛,对此有兴趣的读者可以参考文献[20—22].本文针对清华大学团队最近通过调控量子相变的确定性制备双数态(自旋1/2的平衡Dicke态)的工作背景和研究内容进行讨论.
2 双数态的性质及其在精密测量中的应用
2.1 集体角动量算符以及利用广义Bloch球的量子态表征
对很小的相位偏移(即θ≈0),由于测量会使得量子态以各接近一半的概率塌缩到|0或|1态,通过单次测量是无法判断θ的.也就是说,虽然测量之前的量子态是确定的,探测引发的波函数坍缩引入了测量不确定性,也就是所谓的量子投影噪声.这里涉及到量子态估计的最根本结论,单次测量无法甄别未知的量子态,只有多次测量的统计结果才能描述该量子态.因此,从量子计量的角度而言,在Bloch球上展示指向某个方向的一个态投影到其他方向的量子态的概率,即就显得更有价值(图1(b)), 因为它直接反映了该量子态的测量不确定度.

图1 二能级量子态在Bloch球上的表示 (a)平均自旋的指向;(b)考虑投影噪声,Husimi Q-表示Fig.1. The Bloch sphere representations of the two-level quantum state ≡(a)Representation for the average spin;(b)representation for the uncertainty in the spin direction,or the Husimi-Q representation.
通过对同样条件下制备的单个粒子重复N次实验,或者一次性对N个无关联但是拥有相同量子态的原子系综进行测量,可以提高测量精度.这种所有原子的自旋都指向同一方向的多粒子态被称为自旋相干态,它的波函数可简单标记为由于对这样的原子系综的操控和测量一般都是集体进行的,不区分单个粒子,这样的多粒子态可以很好地通过定义集体自旋算符来描述.在这里,,而代表粒子k的Pauli矩阵算符.Ji满足角动量算符的对易关系,利用(1)式的定义,可以证明自旋相干态的平均集体自旋为单个粒子平均自旋的N倍.而它在垂直于平均自旋方向的投影J⊥为


由于自旋相干态的粒子间没有关联,因此(2)式的第二项为零,,即自旋相干态的横向量子投影噪声涨落为单个粒子的倍.基于上述结果,由N个二能级粒子组成的自旋相干态的最高相位探测灵敏度为(即所谓的标准量子极限).与单粒子态在自旋1/2的Bloch球上的表示一样,自旋相干态的投影噪声∆J⊥同样可以在广义Bloch球(半径为N/2)上表示(图2(a)),其量子投影噪声是各向同性的.
如果我们能够在参与干涉的粒子间引入某种量子关联或纠缠,使得(2)式的第二项为负值,造成,那么就能实现超越标准量子极限精度的测量.其中一种拥有这种关联性质的量子态就是备受关注的自旋压缩态[3,22].顾名思义,该量子态在待测方向上的集体自旋的量子投影噪声较粒子数相同的自旋相干态小,但它在正交于测量方向的量子投影噪声反而更大(图2(b)).因为海森伯不确定性原理,这两者的乘积不变.在过去的十几年中,自旋压缩态已在不同的物理体系中得以实现,利用该量子态实现突破标准量子极限的测量研究也取得了长足的进步.

我们最近的研究则关注了一种被称为双数态(twin-Fock state,TFS)的多体纠缠态.双数态也称为balanced spin-1/2 Dicke态,是由不可区分的双模玻色子组成,拥有相等自旋朝上和朝下粒子数的量子态.由于每个粒子不可区分,每个原子的内态都是全同相干的,我们不能分辨哪个粒子的自旋是朝上或朝下.数学上,双数态可以表示为一种在Bloch球赤道上各个方向的自旋相干态的等权重叠加[23]:因此它也可以利用半径为N/2的广义Bloch球来表征.虽然每一个在Bloch球赤道上的自旋相干态在Jz方向上有投影噪声,但是在双数态这种特殊的叠加条件下,各个自旋相干态在Jz上的量子投影噪声相互抵消,使得∆Jz=0,即沿Jz方向的测量噪声为零.因此双数态在广义Bloch球上表征为一个在赤道上的圆环(图2(c)),像一个过度压缩的自旋压缩态.双数态能实现超越标准量子极限,在理想的探测条件下,达到接近海森伯极限1/N的相位测量精度[24].双数态的特殊性质使得它与自旋压缩态在参数估计的测量方法上有所不同,自旋压缩态可以直接通过测量Jz(即利用Jz的平均值来得到θ,双数态在任何θ下的都为零,它需要通过多次测量Jz来获得Jz的不确定度才能表征θ.

图2 几种不同的集体自旋量子态及其在广义Bloch球上的表示 (a)自旋相干态,所有粒子的自旋都指向同一个方向,该量子态的投影噪声是各向同性的;(b)自旋压缩态,某个方向的量子投影噪声小于同样原子数的自旋相干态的量子噪声,另一个方向的量子投影噪声反而更大(海森伯不确定性原则);(c)双数态,也是自旋1/2的平衡Dicke态,由不可区分的玻色粒子组成,自旋朝上和朝下的原子数目相等,在广义Bloch球表示中,它在纬度方向上的投影没有不确定度(量子投影噪声为零),但是沿经度方向上的分布则完全不确定Fig.2.Representation of a few collective spin states on the generalized Bloch sphere:(a)Coherent spin state,the average spin of every particle points at the same direction,the quantum projection noise is isotropic;(b)squeezed spin state,quantum projection noise along one direction is smaller than that of the coherent spin state with the same atom number,at the expense of enhanced quantum noise along the orthogonal(conjugate)direction;(c)twin-Fock state or spin-1/2 balanced Dicke state,made up of indistinguishable bosons equally distributed in two orthogonal modes(exactly half(N/2)in each mode),its spin direction lies in the equatorial plane,but is completely indeterminate along the azimuthal direction.
另外,在单粒子直积态的表示下,双数态可以表达为
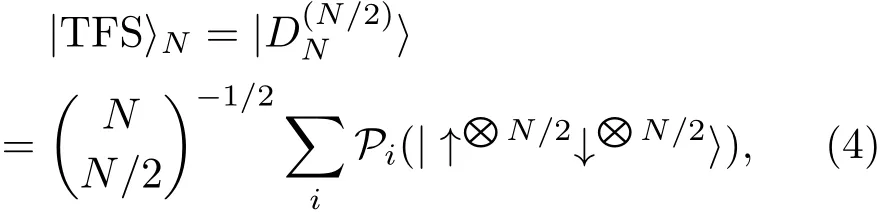
3 双数态的制备
3.1 利用自发参量下转换制备的光子双数态
如果产生一对自发参量下转换光子的概率为p,那么产生N个光子的双数态的概率就大致正比于pN/2.由于p≪1,每增加一对光子的双数态的发生概率就会下降好几个数量级,所以想利用自发参量下转换实现多粒子双数态是非常困难的.另外,由于下转换的光场中充斥着大量的双光子和四光子纠缠态,利用这种方法获得的6光子双数态其实是建立在6个单光子探测器同时触发的条件下的后选择结果.在探测器触发的同时,双数态也被破坏掉了.因此,这样的方法产生的量子纠缠态虽然对基础量子物理研究很有价值,但是却没有实际的量子计量价值.
3.2 利用离子阱量子调控制备的Bell态
离子阱装置可以很好地进行量子计算和量子模拟的实验研究,它实现了目前世界上准确度最高的单量子比特操控和双量子比特逻辑门操作,而且能实现很长的量子退相干时间.因此它也是少有的几个能确定性制备多粒子纠缠态的物理系统之一.但是,通过“由下而上”的量子调控方法制备深度纠缠的多粒子态是极其复杂和困难的.据我们所知,目前利用离子阱制备的“类双数态”依然只停留在两个粒子的Bell态[27,28].2005年,因斯布鲁克的Blatt研究小组[16]实现了8粒子的W态,一种只有一个自旋激发的Dicke态,其表达形式为

之后虽然有一些理论研究提出了利用离子阱制备双数态的操控方法,但是目前还没有相关的实验报道.
由于“由下而上”的纠缠态制备方式过于复杂,以目前的技术而言,想要利用离子阱系统制备对突破标准量子极限测量有实际应用价值的多粒子纠缠态还是比较困难的.目前,离子阱实验最高能确定性制备14个粒子的GHZ态[12].即使在假设完美无误差的情况下,这个量子态能够实现海森伯极限(Heisenberg limit,HL)的测量精度,即∆θHL=1/14,该精度也只等同于约200个粒子的无关联相干态的测量精度.这样粒子数目的相干态在中性原子实验中可以比较容易地实现.
3.3 利用旋量玻色凝聚体中的自旋交换动力学制备双数态
当玻色原子被冷却到极端低温状态时,几乎所有的原子都会凝聚到同一内态上,进入一种被称为玻色-爱因斯坦凝聚体(BEC)的超流状态.如果该BEC被囚禁于一个磁阱中,凝聚体中的原子自旋内态会沿着局域磁场的方向进动,原子的自旋自由度因此被冻结,描述该BEC的序参量是一个标量.反之,如果该BEC被囚禁于一个光阱中,原子的自旋内态可以发生演化.此时,描述一个由F自旋原子组成的BEC的序参量有2F+1个分量.这种量子气体被称为旋量玻色-爱因斯坦凝聚体(spinor BEC)[29].
通过旋量BEC中原子的自旋交换碰撞可以实现大粒子数的双数态.在该碰撞过程中,两个在mF=0磁子能级上的原子发生自旋交换后产生一对mF=±1的原子(图3(a)).由于无法确定自旋交换后某个原子的自旋朝向,碰撞后的粒子对处于两粒子双数态.如果实验中使用了不相干的热原子,又假设碰撞共产生了N个在mF=±1的粒子,那么自旋交换碰撞实际产生了N/2个两粒子双数态.反之,如果自旋交换碰撞发生在BEC中,由于处于BEC状态下的原子无法区分,原则上无法判断是哪两个粒子参与了自旋交换碰撞,而应该说所有的粒子都相干地参与了自旋交换,此时所产生的量子态是一个真正的N粒子双数态.形象上来说,热原子碰撞产生的量子态可以利用N/2个半径为1的Bloch球上的赤道环(图2(c))表示,而在BEC中产生的双数态可以用一个半径为N/2的Bloch球上的大赤道环表示.这两者对量子计量而言有本质上的区别,前者提供的测量精度与标准量子极限相同,而后者能提供超越标准量子极限√倍的测量精度.
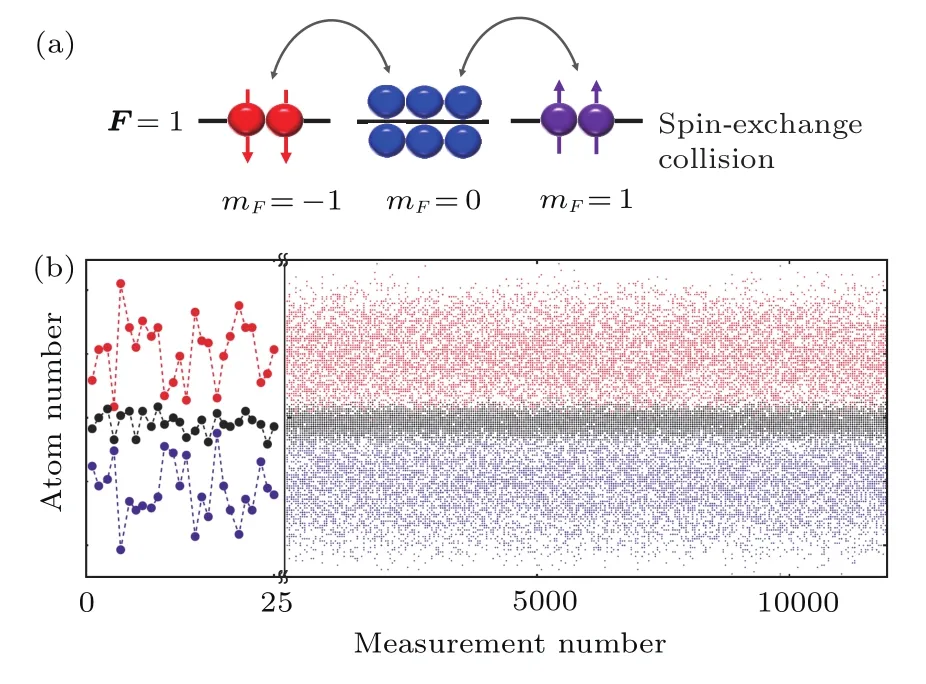
图3 (a)利用旋量BEC中的自旋交换过程制备双数态;(b)利用自旋交换碰撞产生的±1粒子对的关联证明[30];测量到的mF=+1的粒子数(红色)和mF=−1的粒子数(蓝色,取为负值)在不同次实验中展现了很大的涨落,但在同次实验中这两个数之差(黑色)都几乎为零Fig.3.(a)Generation of twin-Fock states using spinmixing dynamics in spinor BEC;(b)illustrating correlated populations in the±1 components generated by spin-exchange collisions.The measured particle numbers in mF=+1(red)and mF=−1(blue,taken as negative)show large fluctuations in different experiment runs,but their difference in any run is always near zero.Figure adapted from Ref.[30].
利用旋量BEC中的自旋交换动力学,过去已经有报导能够实现多达几千个原子的双数态[18,30,31].但是这些实验中产生的双数态的总粒子数存在很大的涨落(见图3(b)),因此以往在利用该双数态演示突破标准量子极限的测量时都需要对样本的总粒子数进行后选择,甚至丢弃超过90%的数据,这大大地降低了这类双数态的实用性.
4 通过调控量子相变实现纠缠态的确定性制备
最近,我们研究团队通过调控自旋1的铷-87原子BEC的自旋混合过程,使其连续发生两次量子相变,确定性地制备了包含约11000个原子的双数态.
在我们的实验条件下[19],该旋量BEC的自旋动力学由下面的哈密顿量描述[32]:

以上哈密顿量描述的旋量BEC在q=±2|c2|处有两个量子相变点.此两点将这个系统的相图分为三个区域:分别为polar(P),broken-axis symmetry(BA),和twin-Fock(TF)双数态相(图4(a)).简言之,该旋量BEC的自旋动力学完全由q与|c2|的比值所决定.当−2|c2|
在以往利用该系统制备双数态的实验中[18,30,31],即使采用了不同的手段和原子内态,实验上总是突然地将q从|q|>2|c2|的状态改变到|q|<2|c2|的状态.如前面所述,这种方法虽然也能产生较大的双数态,但是所产生的双数态粒子数的涨落很大.

图4 (a)自旋1的旋量BEC基态取决于单原子内态的二阶塞曼能移(q)和BEC中自旋交换相互作用强度(c2)的相对大小,依次出现P,BA和TF相;(b)实验观察到的不同自旋分量的原子吸收成像图,给出了线性扫描q时BEC在各个内态上的分布随时间的变化Fig.4.(a)The ground state of a spin-1 BEC is determined by the relative strength between the quadratic Zeeman shift(q)of individual atoms and the spinexchange interaction strength(c2)between them.It can exhibit P,BA and TF phases. (b)The spinresolved absorption images of the atoms that show the evolution of the spin state populations when q is swept linearly over time across the phase transitions.
我们的实验则是精心地设计了q的扫描曲线,让q在有限时间内尽可能慢地穿越量子相变点,使得系统在穿越量子相变点时发生的激发大为减少.其结果是该凝聚体在我们的调控下发生了两次低激发的量子相变,由polar相中的基态进入了双数态相中的低激发态,确定性地将96%±2%的mF=0原子(共约11000个原子)转移到了mF=±1态上(图4(b)).为了更直观地展现本文量子相变方法的制备效率与以前动力学方法的区别,图5给出了类似图3(b)的相应实验数据.在连续制备的420个双数态中,测量显示处在mF=+1和mF=−1态的粒子数分布为5409±200和5427±202个.这两个态的平均粒子数的差别来自不同内态粒子的探测系统误差.而粒子数的均方根涨落一部分来自于0—±1态的转换效率涨落,另一部分则来自BEC总粒子数的漂移和涨落.与±1态的粒子数涨落相比,在+1和−1态的粒子数之差的涨落仅为30.4个,远小于11000个粒子的散粒噪声.而该剩余涨落主要来源于探测原子的成像光的散粒噪声,不是所制备的双数态的自身涨落.

图5 利用调控量子相变所制备的双数态的mF=+1粒子数(红色)和mF= −1的粒子数(蓝色,取为负值)的涨落展示,以及±1粒子数之差(黑色)的涨落展示,插图为粒子数差的放大图Fig.5.Same as Fig.3(b)but for twin-Fock states generated using our method.Inset is a blow-up of the difference in the±1 atom numbers.
由于用缓慢扫过相变点的方法制备的双数态的总粒子数涨落很小,可以在完全不做后选择的情况下测量该双数态的性质.本文的实验表征该双数态的不同内态间原子数的差值的涨落低于经典极限(10.7±0.6)dB,其集体自旋的归一化长度为近似完美的0.99±0.01.这两个指标反映该多体纠缠态可以提供超越标准量子极限约6 dB的相位测量灵敏度,以及至少910个纠缠原子数[19].
5 结 论
利用量子相变确定性地制备多体纠缠态是一种崭新的尝试.由于连续量子相变点处有限系统的能隙很小,系统穿过相变点时会产生较大的激发.我们的研究显示即使这种激发会发生,量子相变点两边迥异的多体能级结构依然能够帮助制备出高品质的多粒子纠缠态.这一全新的理解和纠缠态制备的方法为未来其他多粒子纠缠态的制备提供了一种思路.另外,利用类似的量子相变操控方法,我们最近还成功制备出首个三模的balanced spin-1 Dicke态[33],并利用该态实现了超越三模标准量子极限的干涉测量精度.我们的研究为超越标准量子极限测量的量子计量研究指引了新方向.
