基于原子干涉仪的微观粒子弱等效原理检验∗
2018-09-11王谨1詹明生1
王谨1)2)† 詹明生1)2)
1)(中国科学院武汉物理与数学研究所,波谱与原子分子物理国家重点实验室,武汉 430071)
2)(中国科学院冷原子物理中心,武汉 430071)
1 引 言
广义相对论建立在等效原理和广义协变原理两个基本假设之上.等效原理(也称为强等效原理或爱因斯坦等效原理)包括弱等效原理、局域洛伦兹不变性和局域位置不变性三个部分.弱等效原理(weak equivalence principle,WEP)即自由落体普适性,它有两个等价表述:1)惯性质量等于引力质量;2)自由落体的加速度与其质量和材料无关.迄今为止的大量实验证明,弱等效原理在一定的精度内是成立的.但几乎所有将引力与标准模型统一起来的新理论(如弦理论、圈量子引力理论、额外维理论、非对易几何以及第五种力等)都要求WEP破缺[1].要验证这些新理论、探究WEP的适用范围,就需要开展更高精度的WEP检验.利用宏观物体检验WEP的实验已经达到了较高的精度.宏观旋转落体[2,3]的检验精度为10−7,高塔自由落体[4]的检验精度为10−10,扭秤[5]和激光测月[6]的检验精度为10−13.利用空间微重力环境的“显微镜(MICROSCOPE)”计划通过比较不同材料(钛、铂-铑合金)测试质量的自由下落加速度来检验WEP,检验精度为10−15[7].在微观粒子检验WEP方面,从20世纪60年代以来,人们就在理论和实验两个方面对微观粒子在引力场中的自由落体运动开展了研究.1976年完成的中子干涉仪WEP检验实验的精度为10−4水平[8,9].近年来,原子干涉仪技术[10−13]发展迅速,为利用微观粒子验证WEP提供了新的途径.原子干涉条纹的相位受重力场影响,通过对干涉条纹相位的实验测量,就可以实现对重力加速度的测量.目前,原子干涉仪已广泛应用于重力[14−18]、重力梯度[19,20]、牛顿引力常数[21−24]、精细结构常数[25−27]、转动[28−34]、微弱力[35,36]、引力红移[37]和后牛顿引力[38]的精密测量.原子重力仪与激光干涉绝对重力仪FG-5的对比测量实验[14,39]是在微观粒子与宏观物体之间的WEP检验实验.用原子干涉仪测量、比较不同原子的重力加速度,就可以检验微观粒子的WEP.基于原子干涉法检验WEP[40−47]既是对宏观物体检验实验的补充,又是对WEP检验在微观粒子范畴的扩展.原子干涉仪用量子体系(原子)测量引力,将量子力学与广义相对论直接联系在一起,有利于为促进两大理论的协调提供线索.近十几年,微观粒子WEP检验实验有了较大的进展,这些都得益于原子干涉仪实验技术的发展.
2 原子干涉仪
原子干涉仪的原理类似于光学干涉仪,在原子干涉仪中用原子物质波包取代了光波,用π/2,π拉曼光脉冲取代分束(合)镜、反射镜来实现原子物质波包的分束、反射和合束[10],使物质波包形成干涉.常见的马赫-曾德尔(Mach-Zehnder,M-Z)型原子干涉仪如图1所示,磁光阱制备的基态冷原子团在重力场中自由下落;在t=0时刻,基态冷原子与π/2拉曼脉冲作用后发生拉曼跃迁,处于基态和激发态的叠加态,激发态的原子获得两个光子的反冲动量2k,路径发生改变.在t=T时刻,基态和激发态的原子均与π拉曼脉冲作用,发生内态交换,获得双光子反冲动量2k,路径发生改变;在t=2T时刻,基态和激发态的原子与第二个π/2拉曼脉冲作用,相干合束发生干涉.周期性地扫描第二个π/2拉曼脉冲的相位,探测末态(基态或激发态)的粒子数布居随第二个π/2拉曼脉冲相位的变化,可得到原子干涉条纹信号.如果不考虑重力(g=0,g为重力加速度),则两路原子运动的轨迹没有路径差.受重力的影响(g≠0),原子将沿抛物线运动,两路原子运动的轨迹有重力场导致的额外路径差,原子干涉条纹产生与重力相关的相移,可简单表示为

其中∆φ为相移,g为重力加速度,keff为作用于原子的拉曼光有效波矢,T为π/2,π拉曼光脉冲之间的时间间隔.在重力场中,原子干涉条纹的相对相移与g,keff以及T有关,keff和T是实验设定参数,可以精确控制,只要精确测出原子干涉条纹在重力场中的相位移动值∆φ,就能够实现重力加速度绝对值的精确测量.
用原子干涉仪同时测量并比较不同原子(例如85Rb和87Rb)在重力场中的加速度(g85和g87),二者的差异可以用Eötvös系数表示为

其中η为Eötvös系数,g85和g87分别为85Rb和87Rb原子的重力加速度.如果η=0,则WEP成立.WEP的检验精度取决于重力加速度差分测量(g85−g87)的精度.为减小实验环境的影响,需要将两种原子在空间、时间上严格同步,这样两种原子在干涉过程中经历的共同实验环境噪声(如实验室的振动噪声)和拉曼光相位噪声可以作为共模噪声来抑制.

图1 重力场对M-Z型原子干涉仪的影响Fig.1.In fluence of gravity field on M-Z atomic interferometer.
3 微观粒子弱等效原理检验
自2004年以来,物理学家利用原子干涉仪开展了不同方案的微观粒子WEP检验实验,检验精度在10−4—10−9,Eötvös系数不确定度的直观图如图2所示.根据检验质量的性质,原子干涉仪WEP检验实验可分为两类:1)不同状态的原子;2)不同质量的原子.

图2 基于原子干涉仪的微观粒子弱等效原理检验实验Eötvös系数的不确定度 MPQ,马普量子光学研究所;ONERA,国家航天研究室;LUH,莱布尼茨汉诺威大学;UF,佛罗伦萨大学;WIPM,武汉物理与数学研究所;HUST,华中科技大学;UB,波尔多大学Fig.2.Uncertainties of η in microscopic particles weak equivalence principle test based on atom interferometry.MPQ,Max Planck Institute of Quantum Optics;ONERA,The National Office for Studies and Aerospace Research;LUH,Leibniz University Hannover;UF,University of Florence;WIPM,Wuhan Institute of Physics and Mathematics;HUST,Huazhong University of Science and Technology;UB,University of Bordeaux.
3.1 不同质量的原子
2004年,德国马普量子光学研究所的Fray等[40]首次利用原子干涉仪开展了微观粒子WEP的检验实验,他们利用布拉格衍射完成原子的外态干涉,分别测量了85Rb和87Rb原子的重力加速度值,获得的Eötvös系数为η =(1.2± 1.7)× 10−7,η值的不确定度为1.7×10−7.由于对85Rb和87Rb原子进行非时间同步测量,未采取共模噪声抑制措施,相位噪声、振动噪声大,信噪比差.2013年,法国国家航天研究室的Bonnin等[41]利用同步85Rb-87Rb双组分原子干涉仪开展了WEP检验实验,拉曼光的光频移及地球转动引起的系统误差仍然较大,获得的Eötvös系数为η =(1.2± 3.2)× 10−7.2014年,德国莱布尼茨汉诺威大学的Schlippert等[42]开展了非同位素(87Rb和39K)原子干涉仪WEP检验实验,87Rb和39K的有效波矢相差较大,两种原子的上抛和下落过程在时间上同步,但在空间位置上有差异.为了消除原子空间不同步带来的系统误差,他们交替地对87Rb(39K)原子进行向上、向下反冲,取相邻两次反冲测量的平均值作为87Rb(39K)原子的绝对重力加速度,获得的Eötvös系数为η=(0.3± 5.4)× 10−7,测量精度主要受39K原子制约.此后不久,意大利佛罗伦萨大学的Tarallo等[43]利用光晶格中锶原子的费米子同位素87Sr和玻色子同位素88Sr开展了WEP检验,实验结果为η=(0.2±1.6)×10−7.中国科学院武汉物理与数学所的Zhou等[44]提出并实现了一种四波双衍射拉曼跃迁(four-wave doublediffraction Raman-transition,FWDR)原子干涉方案,解决了85Rb-87Rb双组分原子干涉中多频光串扰问题,抑制了共模噪声,获得的Eötvös系数为η=(2.8±3.0)×10−8.
3.2 不同状态的原子
除了采用新方案或者发展新技术来不断提高现有WEP检验的精度外,探索可能引起WEP破缺的新机理并进行实验检验也是一个重要发展方向.用不同自旋取向的原子检验WEP对探索自旋相关的量子引力问题有重要意义.2016年,华中科技大学的Duan等[46]完成了这种不同自旋取向原子(87Rb,mF=±1)WEP的实验检验,实验精度达到10−7水平,η=(0.2±1.2)×10−7.意大利佛罗伦萨大学Rosi等[47]利用叠加态原子进行了WEP检验,他们将铷原子制备到两个超精细态以及它们的相干叠加态,利用布拉格衍射形成原子干涉仪,通过测量自由下落的铷原子处于不同内态及其叠加态时重力加速度的差异来检验WEP,实验获得的Eötvös系数为η =(3.3±2.9)×10−9.
4 双组分原子干涉仪弱等效原理检验实验的关键问题

图3 主动隔振系统测试数据[48] 系统与主要噪声源隔离并降低环境噪声前(a)后(b)获得的数据;对数纵坐标为地震仪测量的等效加速度噪声,黑线为反馈回路关闭时被动平台上的振动噪声,蓝线为内回路地震仪测得的残余振动,红线表示反馈打开时外回路的测量结果Fig.1.The performance of our active vibration isolation[48].The data acquired before(a)and after(b)we isolate the whole system from the main noise source and decrease the environmental noise.The logarithmic vertical axis shows the equivalent acceleration noise measured by the seismometer.The black line represents the vibrational noise on the passive platform with the feedback loop o ff,while the blue line represents the residual vibration measured by the in-loop seismometer and red line is the out-loop measurement with the feedback loop on.
在不同体系、不同方案的原子干涉仪WEP检验实验中存在诸多不同来源的噪声,需要逐一克服.原子干涉仪WEP检验实验需要首先解决的关键问题主要有振动噪声的抑制、拉曼光频率的控制、拉曼光相位噪声的抑制、双组分原子干涉共模噪声抑制、信号探测与数据处理方法.
4.1 振动噪声的抑制
在原子干涉仪中,振动噪声通过拉曼光反射镜传递到原子干涉条纹的相位中.为了降低原子干涉仪的相位噪声,需要将拉曼光反射镜与环境振动源隔离.原子干涉仪对频率低于1/T的振动更敏感,即低频振动噪声对原子干涉测量造成的不利影响最大.为了提高原子干涉仪WEP检验实验的精度,需要将拉曼光反射镜安装在性能良好的低频隔振系统上.为有效抑制原子干涉仪中0.01—10 Hz的低频振动噪声,Tang等[48]发展了一种可程控宽带低噪声主动隔振技术,采用这种技术的主动隔振系统能将背景的振动噪声抑制两个量级,使0.01—10 Hz频段的振动噪声谱密度低至水平,实验结果如图3所示.图4是采用主动隔振系统前后一组原子干涉条纹的对比,可以看出采用主动隔振系统后,原子干涉条纹的短期稳定性有明显提高.

图4 主动隔振工作时T=70 ms的原子干涉条纹得到显著改善[48]Fig.4.The atom interference fringe of T=70 ms is greatly improved after active isolation is on[48].
4.2 拉曼光频率的控制与相位噪声的抑制
在原子干涉仪中,为减小光频移的影响,需要增大并调节拉曼光的失谐量.通常用声光调制器(acousto-optic modulator,AOM)或电光调制器(electro-optic modulator,EOM)调节激光的失谐量.常用AOM的移频量一般低于5 GHz,不能满足大多原子干涉仪拉曼光移频的需求,而更高频的声光调制效率极低.Peng等[49]利用10 GHz的光纤EOM实现了一种新的拉曼光移频、稳频方案(图5),将光纤EOM的载波或任一高阶边带(最高可到四阶)锁定到原子参考谱线上,扫描EOM的驱动频率(0—10 GHz),可以将输出激光的频率设置在80 GHz(−40—40 GHz)范围内的任意点,解决了拉曼光的大失谐频率锁定问题.

图5 拉曼光大失谐频率锁定实验方案[49] DL,二极管激光器;MG,微波发生器;HM,半反镜;EC,控制电路Fig.5.Experimental scheme for frequency stabilization of far-detuning Raman lasers[49].DL,diode laser;MG,microwave generator;HM,half-reflection mirror;EC,circuit controller.
原子干涉仪的相位噪声由灵敏度函数和拉曼激光的相位噪声决定,相位噪声会在整个频率范围内累积.高精度原子干涉仪需要拉曼光在整个频率范围内具有较低的相位噪声.光学锁相环(optical phase lock loop,OPLL)方案产生的拉曼光在低频范围(<100 kHz)具有很低的相位噪声,但由于受伺服反馈电路带宽的限制[50],在高频范围(>100 kHz)的相位噪声较大.用电流调制或相位调制方案产生的拉曼激光的相位噪声主要受调制器微波驱动信号性能的限制.例如,在电光调制和电流调制中,一些不需要的冗余边带不能在空间上分开,冗余边带的交流斯塔克频移会在原子干涉重力测量中引入系统误差[51,52].AOM产生的拉曼激光在高频范围的相位噪声较低,但受分立光学元件振动噪声的限制,拉曼激光在低频范围内的相位噪声较大.Wang等[53]用AOM与OPLL组合方案实现了宽带、低相噪拉曼光的制备.在该方案中,用1.52 GHz AOM的±1阶衍射光作为频率差为3.04 GHz的一对拉曼激光,通过反馈控制来抑制相位噪声.在低频段,拉曼激光的相位噪声被抑制了35 dB;在高频段,相位噪声小于−109 dBc/Hz.由于拉曼光的高频响应特性改善,原子干涉仪的灵敏度不再受拉曼脉冲持续时间的限制,因此使用组合方案制备的拉曼激光可以将原子干涉仪灵敏度提高.
当拉曼光与原子相互作用时,拉曼光束的波前畸变会在原子干涉信号中引起相位噪声.Louchet-Chauvet等[54]测量了拉曼光束波前畸变导致的相位噪声.Schkolnik等[55]研究了拉曼光束波前畸变对原子干涉测量的具体影响.Zhou等[56]通过调制拉曼光束的尺寸测量了波前畸变对原子干涉测量的影响.为了抑制拉曼光束波前畸变相位噪声,Hu等[57]针对双组分原子干涉仪检验WEP实验,提出了一种扩展速率选择方案来抑制同位素和非同位原子干涉仪中的波前畸变相位噪声.利用这种方案可以将波前畸变噪声抑制10倍.
4.3 双组分原子干涉共模噪声抑制
共模测量是消除测量误差和共模噪声的有效途径,在采用如图6(a)所示的传统单衍射拉曼跃迁原子干涉过程中,由于原子干涉的路径不对称,在双组分原子干涉测量中重力梯度的影响无法完全抵消,不同频率拉曼光之间的串扰也会引入相位噪声.Lévèque等[58,59]为了改善单组分原子干涉仪的相位噪声采用了一种双衍射拉曼跃迁技术.Zhou等[44]将双衍射拉曼跃迁技术应用到双组分原子干涉仪中,提出并实现了FWDR原子干涉仪方案,该方案选用四束拉曼激光来构成两组拉曼激光,四束拉曼激光的频率依次为ω1,ω2,ω3和ω4,ω1和ω2为85Rb和87Rb原子的共用拉曼光,ω3和ω4分别为85Rb和87Rb原子的专用拉曼光,通过选取ω1,ω2,ω3和ω4的最佳频率值、优化四束拉曼激光的光强比例,可以消除拉曼光的交流斯塔克频移.FWDR原子干涉方案如图6(b)所示,原子的干涉路径完全对称,重力梯度的影响可以在较大程度上抵消.由于FWDR构型的干涉环路只涉及同一个内态,不同内态的影响也被减小.以87Rb原子为例(85Rb与此类似)来说明干涉过程.首先需要制备四束拉曼激光来构成两组拉曼激光对,四束拉曼激光的波矢依次为k1,k2,k3,k4.拉曼激光的频率满足条件:
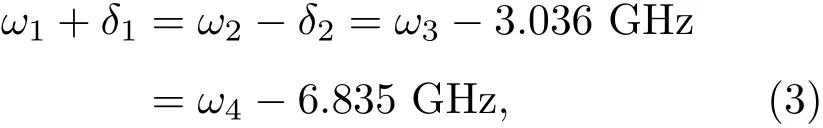
其中δ1,δ2分别是ω1,ω2的失谐量,且δ1= −δ2.如图6(b)所示,两组拉曼激光的有效波矢的方向相反,当这样的两组拉曼脉冲与初态|F=1,mF=0的原子作用时,原子将被转移到|F=2,mF=0态,同时获得方向相反的反冲动量.原子依次经过双衍射拉曼跃迁脉冲序列,实现分束、反射、合束,最后完成干涉.处于态的原子数布居将包含干涉条纹的相位信息.
利用FWDR方案抑制相位噪声的实验数据及对比数据如图7所示.图7(a)为通过快速相位调制对85Rb原子的拉曼光施加模拟相位噪声后,用传统单衍射拉曼跃迁获得的85Rb,87Rb原子干涉条纹,受人为模拟相位噪声的影响,85Rb原子干扰条纹消失.图7(b)为施加模拟相位噪声后用FWDR方法获得的85Rb,87Rb原子干涉条纹,可以看出85Rb原子干涉条纹的对比度为20%,对相位噪声有很好的免疫力.利用这种FWDR双组分原子干涉仪方案检验WEP的统计不确定度优于1×10−8水平[44](表1).

图6 两种原子干涉环路的示意图 (a)单衍射拉曼跃迁构型;(b)双衍射拉曼跃迁构型Fig.6.Schematic diagram of two atomic interference loops:(a)Single-diffraction Raman transition configuration;(b)double-diffraction Raman transition configuration.

图7 FWDR方法对相位噪声的抑制效果[44] 对85Rb原子施加快速相位调制后,用传统单衍射拉曼跃迁获得的85Rb,87Rb原子干涉条纹(a)和用FWDR方法获得的85Rb,87Rb原子干涉条纹(b).红色三角形是85Rb原子干涉条纹的实验数据,红色点线是正弦拟合曲线;蓝色圆点是87Rb原子干涉条纹的实验数据,蓝色实线是正弦拟合曲线Fig.7.Phase noise suppression by the FWDR method[44].A rapid phase modulation is applied to85Rb atoms.(a)Simultaneous85Rb-87Rb interference fringes obtained by single-diffraction Raman transition method and(b)simultaneous85Rb-87Rb interference fringes by the FWDR scheme.The red triangles are experimental data points of85Rb atoms,and the red dotted line is a sine curve fitting.The blue dots are experimental data points of87Rb atoms,and the blue solid line is a sine curve fitting.

表1 影响重力加速度差分测量的主要因素[44]Table 1.Main contributions a ff ecting the differential gravitational acceleration measurement[44].
4.4 信号探测与数据处理
在原子干涉精密测量实验中,由于背景磁场、环境温度、激光强度、激光频率等实验参数的波动,磁光阱制备的冷原子数目、参与干涉过程的冷原子数目都会随时间波动,这些波动在原子干涉信号中以幅度噪声的形式呈现出来.不过,就每一次干涉过程而言,处于两个基态超精细能级之一的原子数占原子总数的比例是一定的,因此可以通过归一化探测来抑制幅度噪声.传统的归一化探测方案有两态顺序探测[60]和两态同时探测[61,62]两种.两态顺序探测将处于两个基态的原子波包在时间上分离探测,这需要更多的时间,使得探测程序复杂.两态同时探测将处于两个基态的原子波包空间上分离探测,需要探测激光束的直径比原子团尺寸大50%[62],如果激光束尺寸较小,则会对原子温度或自由演化时间造成额外限制.Song等[63]提出并实现了一种简单的原子干涉信号归一化探测方案,利用初态制备期间的淬灭荧光信号对原子末态布居数进行归一化探测,使得探测系统和探测过程大为简化,从而降低了原子干涉幅度噪声.
为准确处理双原子干涉仪(重力梯度仪)的差分相位数据,通常采用三种方法:最小二乘拟合[64],椭圆拟合[65]和贝叶斯估计[66].最小二乘拟合只适用于共模相位噪声较低的情况;椭圆拟合可以抑制常见的相位噪声,但在差分相位测量中系统误差是非线性的,差分相位过大或过小时,拟合误差都较大,差分相位为π/2的奇数倍时拟合误差最小.为了通过椭圆拟合方法测量微小的相位差,可施加偏置磁场来增大双原子干涉仪的差分相位,使其接近π/2,典型的数据如图8(a)所示.然而,偏置磁场引入的相位的不确定性又会带来差分相位测量的系统误差.贝叶斯估计方法处理差分相位更加准确,但它需要先验相位噪声模型[67].为减小差分相位拟合的误差,Barrett等[68]以及Pereira Dos Santos[69]对椭圆拟合和贝叶斯估计做了修正.Wang等[70]提出了一种用于提取原子重力梯度仪差分相位的组合方案,即只调制其中一个原子干涉仪的磁场,再利用椭圆和线性拟合的方法提取双原子干涉仪的差分相位,这样就能够在较大的噪声环境下准确提取出小额差分相位,弥补椭圆拟合方法和贝叶斯统计方法的不足.这个方法可推广到双组分原子干涉仪WEP检验研究中,不过双组分原子干涉仪在空间、时间上同步,无法单独调制其中一个原子干涉仪的磁场.替代方案是通过微调自由演化时间T,使不同组分原子干涉仪的相位差接近π/2的奇数倍,以此来减小椭圆拟合误差[44].
试图统一量子力学与引力的标量-张量场的理论认为,各种元素之间的WEP破缺系数和组成它们的中子的数目和种类相关,相比于同位素原子,非同位素原子之间具有更大的WEP破缺系数[71].例如,铷-钾之间的WEP破缺系数比铷同位素之间的大20倍,因此非同位素原子更适于检验标量-张量场理论.但是现有的原子干涉WEP检验计划大多采用同位素原子,原因是非同位素原子之间的振动噪声难以共模抑制,这限制了非同位素原子干涉仪检验WEP的精度.Chen等[72]分析了振动导致的原子干涉条纹噪声,利用双组分原子干涉仪振动噪声的关联性,提出了一种比例扫描位相方案,可以共模抑制任意双组分原子干涉仪的振动噪声,共模抑制比高达140 dB.采用比例扫描位相方案可得到一个没有显式表达式的李萨如图,如图8(b)所示.利用新设计的贝叶斯估计算法对图8(b)中的数据进行相位差估计得到的标准差如图9所示.比例扫描位相方案有利于得到WEP破缺系数的最优无偏估计、拓展WEP检验候选的原子范畴、提高标量-张量场理论的检验精度.Hu等[73]针对双组分原子干涉仪检验弱等效原理实验,提出了一种抑制拉曼光波前畸变噪声的方案,有利于在弱等效原理检验实验中抑制拉曼光波前畸变噪声、提高检验精度,基于适当的实验参数进行的模拟表明,使用85Rb-87Rb和41K-87Rb的WEP检验实验中波前像差引起Eötvös系数的标准偏差分别为1.3×10−14和3.0×10−13.
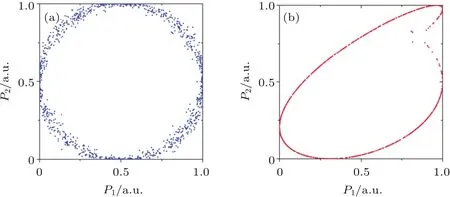
图8 双原子干涉仪布居数的椭圆拟合 (a)采用同步扫描得到的椭圆;(b)采用比例扫描得到的李萨如图[72]Fig.8.Ellipse fitting of population in two atom interferometers:(a)Ellipse figure obtained with synchronous and(b)Lissajous figure obtained with proportional scans[72].

图9 采用贝叶斯估计方法得到的位相差估计的标准差[72]Fig.9.Standard deviation of phase difference estimation using Bayesian estimation method[72].
5 微观粒子弱等效原理检验研究的发展趋势
目前,原子干涉法检验WEP的实验精度比早期利用中子检验WEP的精度提高了5个量级,但仍未发现微观体系WEP的破缺,因此有必要开展更高精度的WEP检验.原子干涉仪的灵敏度取决于参与干涉过程的原子数目和原子自由演化时间.提高微观粒子WEP检验精度有三个发展趋势:一是利用长基线原子干涉仪或空间微重力环境提高原子的自由演化时间;二是降低原子的温度、减小原子团的发散,以此来增加参与干涉测量过程的原子数目;三是制备纠缠态原子源、克服标准量子极限,提高测量精度.
5.1 长基线原子干涉仪
长基线原子干涉仪是增加原子自由演化时间的一种有效途径.美国斯坦福大学的大型原子喷泉的最大上抛高度达9 m[33,74],磁屏蔽内的有效干涉区为8.2 m,最长自由演化时间可以达到1.34 s,这为提高WEP的检验精度创造了条件[75,76].德国莱布尼茨汉诺威大学设计的铷-镱双组分原子干涉仪[77],高度为10 m、磁屏蔽内的有效干涉区为9 m,目前还在建设之中.法国波尔多大学正在建设原子干涉仪阵列[78],拟开展引力波探测研究.武汉物理与数学所研制的用于高精度WEP检验的10 m原子干涉仪[79]如图10所示,10 m原子干涉仪由下磁光阱、喷泉管、上磁光阱三大部分组成,整个系统高达12 m,磁屏蔽区内原子有效干涉区为10 m.2011年获得了上抛高度为6 m原子喷泉信号[79],近期获得的上抛高度为12 m的原子喷泉飞行时间信号如图11所示.为了进一步提高原子干涉仪WEP检验的精度,美国斯坦福大学提出了建造100 m量级[75]的大型原子干涉仪的设想.利用长基线原子干涉仪开展微观粒子WEP的高精度检验,可能会导致广义相对论的修正,或为量子引力理论提供支持.

图10 10 m喷泉式原子干涉仪示意图Fig.10.Schematic diagram of the 10-meter fountain type atom interferometer.

图11 上抛高度为1—12 m的原子喷泉飞行时间信号Fig.11.Time of flight signal of fountains with launching height of 1–12 m.
5.2 空间原子干涉仪
微重力环境下原子自由下落的时间很长,让原子干涉仪装置自由下落[80],或者将原子干涉仪置于卫星[81,82]或空间站[83]可延长原子自由演化时间.2016年,法国波尔多大学的Barrett等[45]将87Rb和39K原子干涉仪置于飞机上(图12),利用飞机在抛物线飞行过程中的微重力条件开展了检验WEP的演示实验,在飞机稳定飞行期间测得的Eötvös系数的不确定度为1.1 × 10−3,在0 g环境测得的Eötvös系数为η =(0.9± 3.0)× 10−4. 这次实验是对星载原子干涉仪WEP检验计划“STEQUEST”[81,82]关键技术的验证.
5.3 超冷原子的制备
在原子干涉仪检验WEP的结果中,影响测量不确定度的因素之一是原子的温度.如果原子温度不够低,参与干涉过程的原子数不够多,则原子干涉信号信噪比就差.因此,需要尽可能地降低原子的温度、减小两种原子的初始速度与位置的涨落.在温度更低的气体中,不同原子间的速度涨落更小,原子团在自由飞行过程中的膨胀也更慢,这样就能在WEP检验实验中将原子抛得更高,使原子的自由演化时间更长、原子干涉仪的测量灵敏度更高.
为了制备超冷(<1µK)原子,在实现磁光阱冷却后,一般要将原子载入磁阱或光阱中进行蒸发冷却.要提高蒸发冷却的效率,原子间应有足够大的弹性碰撞散射截面和足够小的非弹性碰撞散射截面,其中,前者能让原子气体更快地达到热平衡,而后者则让原子的损耗率更小.由于85Rb原子的s波散射长度在温度为350µK时有个零点,这使得85Rb原子在蒸发冷却温度范围的碰撞散射截面过低.另外,85Rb原子的非弹性三体损耗的散射截面过高,要实现超低温、高密度的85Rb子气体极其困难.因此,进一步理解85Rb原子的碰撞散射性质,寻找降低85Rb损耗的方法,对于制备85Rb和87Rb超冷原子混合气体十分重要.Dong等[84]从理论和实验上研究了85Rb和87Rb原子在不同散射通道内的Feshbach共振,这一研究结果有助于制备超冷高密度的85Rb和87Rb混合气体.

图12 飞机失重环境中的双组分原子干涉仪弱等效原理检验实验示意图[45] (a)飞机抛物线飞行的基本轨迹;(b)安装在飞机上的原子干涉仪;(c)87Rb-39K原子同步双干涉仪示意图Fig.12.Schematic diagram of the experimental test of the weak equivalence principle using dual atom interferometers in an aircraft weightless environment[45]:(a)Basic trajectory during parabolic flight;(b)atom interferometers onboard the aircraft;(c)schematic of the simultaneous87Rb-39K dual atom interferometers.
5.4 纠缠态原子的制备
基于原子干涉仪的WEP检验精度受限于标准量子极限.如果能制备纠缠态原子并将其用于原子干涉精密测量,可望突破标准量子极限、提高测量精度.Zeng等[85]将铷原子相干激发到里德伯态,充分利用85Rb和87Rb在光谱频率上的差别实现了对单个原子的寻址及操控,通过里德伯阻塞实现了异核单原子的纠缠态制备.如果原子干涉仪的输入态是由N个没有关联的原子组成的经典态,这等同于对同一个原子进行N次测量,那么测量精度最终将受限于标准量子极限利用原子之间的量子关联(比如自旋压缩态)可以实现超越标准量子极限的测量精度,而最大纠缠态NOON态和Dicke态可以实现接近海森伯极限的测量精度1/N,但目前这种量子态只在离子、光子和核自旋体系上有成功的实验报道,最多对应了10个左右的粒子.Luo等[86]通过调控量子相变过程制备了大粒子数(接近10000个)双数态(twin-Fock)原子玻色-爱因斯坦凝聚体,这是一种原子在两个模式上具有同等粒子数的多体纠缠Dicke态.这些工作为利用纠缠资源提高双组分原子WEP的检验精度奠定了基础.
6小 结
提高现有实验方案的检验精度是WEP检验实验研究的重要目标,而探索可能引起WEP破缺的新机理并进行实验检验是另一个重要方面.自2004年以来,微观粒子WEP检验的实验研究取得了重要进展,用不同质量原子(85Rb-87Rb,87Sr-88Sr,87Rb-39K)检验WEP的精度从10−7提高到10−8水平[44],用不同自旋取向原子(87Rb,mF= ±1)检验WEP的精度达到10−7水平[46],利用叠加态原子的WEP的量子检验精度达到了10−9水平[47].Gao等[87]还利用85Rb和87Rb双组分原子干涉仪弱等效原理的实验结果给出了验证广义不确定性原理的Kempf-Mangano-Mann和Maggiore两种方案的参数上限.在振动噪声的抑制、拉曼光的移频与相位噪声抑制、FWDR原子干涉新方案、信号探测与数据处理等一些原子干涉仪WEP检验实验的关键方法与技术方面取得了突破.长基线原子干涉仪[33,76,78]的建设取得了进展,失重条件下用原子干涉仪检验WEP的演示实验精度到达了10−4水平[45],更高精度的空间原子干涉仪WEP检验计划[80,81]也正在实施之中.旨在超越标准量子极限的原子源制备技术也取得了突破[84,85].随着研究工作的深入开展和实验技术的进步,基于长基线原子干涉仪或空间原子干涉仪的微观粒子WEP检验的精度有望在将来达到10−15—10−17[74]的水平.
