近距离牛顿反平方定律实验检验进展∗

谭文海 王建波 邵成刚 涂良成 杨山清†罗鹏顺‡ 罗俊2)††

1)(华中科技大学物理学院,基本物理量测量教育部重点实验室,引力与量子物理湖北省重点实验室,武汉 430074)

2)(中山大学天琴引力物理研究中心,珠海 519082)

1 引 言

目前物理学界公认自然界存在四种基本相互作用,分别是引力、电磁力、强相互作用和弱相互作用,其中引力是近代物理学中最早被认识的相互作用.牛顿于1687年在《自然哲学的数学原理》中提出万有引力定律,将天体的运动规律与地面自由落体的规律统一起来.爱因斯坦的广义相对论将引力描述为物质和能量引起的时空弯曲所导致,而牛顿万有引力定律是静态、缓变的弱引力场下的近似.作为迄今描述引力最成功的理论,广义相对论得到了各种实验与天文观测的检验:包括水星近日点进动、光线在太阳引力场作用下的偏折效应、引力红移效应的观测等,其预言的引力波现象也被激光干涉引力波天文台LIGO于2016年直接探测到[1],2017年MICROSCOPE卫星在更高精度[−1± 9(stat)± 9(syst)]× 10−15水平[2]证明其基本原理——弱等效原理的正确性.另一方面,粒子物理标准模型把电磁力与强、弱相互作用统一起来,精确地描述了微观世界的各种物理现象.建立包含引力的大统一理论是物理学的前沿问题之一,但广义相对论是“经典”理论,引力仍然没有被成功地量子化,与粒子物理标准模型本质上并不兼容.典型的困难是等级问题:引力量子效应凸显的能量标度——普朗克能量标度是1.2×1016TeV,而电弱统一的能量标度约1 TeV,两者相差16个数量级[3,4];天文观测表明,宇宙正在加速膨胀,这种加速膨胀可以引入暗能量来解释.然而,科学家发现天文观测到的暗能量密度比根据量子理论计算的真空能量密度小约1060倍(以电弱统一能标作为能量截断计算)[5−7].

为此,物理学家们提出了很多理论模型,其中很多理论认为牛顿反平方定律在近距离下会破缺.如1998年Arkani-Hamed等[3]和Antoniadis等[8]提出大额外维理论,认为时空存在额外维空间,引力子可以在包括额外维空间的全空间自由传播,而标准模型的粒子只能在我们熟悉的3+1维时空里传播.若所有n个额外维的尺度R∗相同,在间距r≫R∗范围,牛顿反平方定律成立;在r≪R∗范围,反平方定律变成正比于1/r2+n;在r≫ R∗范围,引力势可引入Yukawa形式的修正[9]:

式中G为万有引力常数;m1,m2为物体的质量;α是破缺效应的作用强度;λ是作用程.

此外,弦论及其他非标准模型理论预言了新的玻色子的存在,如moduli,dilaton[10−12]和axion等[13].粒子间通过交换这些新的玻色子可产生新的有效相互作用,使引力偏离牛顿反平方定律[5].因此,在近距离下对牛顿反平方定律进行高精度的实验检验,寻找可能存在的新相互作用,一方面可以检验引力理论的正确性,另一方面也可探索非标准模型的新物理,为统一理论的建立提供实验依据和指导,因而具有重要意义.

2 实验检验概况

最早进行牛顿反平方定律的检验实验可以追溯到1798年,Cavendish声称他在测G实验中同时检验了反平方定律,但并没有给出任何实验细节.Mackenzie[14]在1895年采用扭秤检验了牛顿反平方定律,这是首次公开发表的实验结果.广泛引起人们检验牛顿反平方定律兴趣的是Long[15]的实验:1974年,他在《Physical Review D》上发表了题为“为什么我们要相信实验室尺度下的牛顿引力呢？”的文章,通过对近百年各种测G实验结果的研究后发现:G(R)=G0[1+0.002lnR].两年后,Long[16]再次在《Nature》杂志上发表了他利用扭秤测量不同间距下的两个圆环的牛顿引力大小的实验结果,发现牛顿引力的测量值与理论值的偏差在(0.37±0.07)%的水平,该结果与他之前分析出的G值与距离R相关的结论符合.虽然Long的实验结果被后来的实验所否定,但该结果引起了物理学家们的广泛关注,使对牛顿反平方定律的实验检验活跃起来.

当前,物理学家们已经在很宽的尺度下对牛顿反平方定律进行了实验检验.不同理论模型预言的反平方定律破缺强度与作用程范围均不相同,针对不同的尺度需要采取不同的实验检验办法.在厘米到亚毫米尺度主要使用精密扭秤作为测量工具[17−23],在此范围下,实验检验精度已远小于牛顿引力,如何精确补偿与评估牛顿引力干扰是关键.在微米范围下,主要采用微机械振子和悬臂梁作为弱力测量工具[24−32],此时Casimir力和静电力成为主要的干扰信号,如何消除Casimir力和静电力的影响是实验需要解决的关键问题;在纳米及以下尺度可通过中子散射实验或原子核的结合能与电荷半径等性质给出[33−38],在更大尺度则可通过不同地点的重力加速度测量、天体或卫星的运动轨迹等观测数据给出,更详细的介绍可参考文献[39—47].近距离下检验牛顿反平方定律的实验结果如图1所示[19−32],图中右上角的浅色区域为牛顿反平方定律仍然成立的参数空间,左下角空白区域有待更高精度的实验进行检验,本文重点介绍亚毫米与微米范围的实验.

图1 近距离检验牛顿反平方定律的实验结果Fig.1.Constraints on the violation of the Newtonian inverse-square law at short range.

在厘米范围,加州大学Irvine分校的Spero等[48]用扭秤检验物体在一长空心不锈钢圆管内受到的引力是否满足反平方定律.若牛顿反平方定律成立,则管内的引力势基本相同,小铜柱所受的引力几乎为零,水平往返移动圆管的过程中扭秤几乎不发生偏转,结果表明在检验质量与吸引质量的间距为2—5 cm范围内均未发现反平方定律破缺.由于该实验对Long提出的真空极化效应[49]不灵敏,他们又进行了引力不为零的实验[19],实验原理是将大小不同的吸引质量放置在离扭秤距离不同的位置,其中大吸引质量重7.3 kg,距离扭秤中心105 cm,小吸引质量重43 g,距离扭秤中心5 cm,如果反平方定律严格成立,它们对扭秤产生的引力将相互抵消,扭秤受到的总力矩不变.该实验检验精度比1980年的实验提高了约5倍,结果表明在作用程λ>400 mm范围,仍然没有发现牛顿反平方定律的破缺.

华中科技大学引力中心长期进行近距离牛顿反平方定律的检验实验,该研究组利用厚度0.2 mm的金片作为吸引质量与检验质量,以扭秤为工具进行间距调制实验,于2007年完成了亚毫米范围牛顿反平方定律的零检验实验[21].实验使用的扭秤左右对称,检验金片黏在扭秤的一端,面对吸引金片,扭秤另一端面对引力补偿块.通过设计检验金片离吸引金片距离较近,但质量较小,而补偿质量离扭秤距离较远,但质量较大,可使吸引质量与补偿质量对扭秤的牛顿引力矩刚好抵消,但非牛顿引力因随间距增大以e指数衰减,因此不会被抵消.检验质量与吸引质量的间距调制范围从176µm到341µm,实验中同步驱动一个小铜柱产生确定的引力源实时标定扭秤的灵敏度.实验在2σ精度内未发现牛顿反平方定律的偏离,若要求破缺强度|α|>1,则作用程λ要求小于66µm,接近当时国际最好水平.在毫米范围,为了增加待测效应,该研究组改进了实验方案[22],将检验质量与吸引质量钨片的厚度增大为1.787 mm,间距调制范围为0.4—1.0 mm.由于质量增大,对各部件的加工误差要求也相应提高,这也成为此实验的难点之一.实验通过“零”实验设计与精密加工装配,牛顿力矩误差被控制到(0.65±1.59)×10−16Nm,其中钨片厚度精度为0.12µm,扭丝定位精度为1.5µm;通过改进电磁屏蔽,解决了平移台的电磁干扰问题.此外,进行了“非零”实验,测量了牛顿引力矩随吸引质量间距的变化,以此验证系统的可靠性.最后在2σ力矩精度为2.6×10−16Nm下未发现牛顿反平方定律的偏离,在作用程λ为3 mm附近取得检验精度最高的实验结果.

华盛顿大学Eöt-Wash研究组也长期使用扭秤在亚毫米范围检验牛顿反平方定律[9,20],他们实验的主要特点是检验质量与吸引质量均为轴对称的多重密度调制结构.检验质量通过扭丝水平悬挂,吸引质量安装于检验质量正下方,通过匀速驱动吸引质量旋转,将待测信号调制到驱动频率的高倍频,从而降低系统干扰.以2007年的实验为例,其检验质量圆盘轴对称地分布有21个圆孔,吸引质量则由两层各有21个圆孔的圆盘叠在一起构成,上下两层圆孔的方位角错开π/21,从而部分抵消了牛顿引力,有助于提高实验精度.扭秤与吸引质量有良好的接地与静电屏蔽措施,以降低静电干扰.该实验间距为55µm—9.53 mm,结果表明在作用程λ为56µm的尺度下牛顿反平方定律仍然成立(即破缺强度|α|6 1),对于一个额外维的模型,实验要求额外维尺度R∗6 44µm.在其改进实验中,扭秤与吸引质量的对称性提高到120重,以进一步提高实验精度.

科罗拉多大学Long等[24,50]使用机械振子在几十微米的间距检验了非牛顿引力.他们采用35 mm×7 mm×0.305 mm的钨悬臂梁作为吸引质量,由压电陶瓷(PZT)驱动其振动,检验质量位于吸引质量下方,由两块对称的矩形钨片构成,钨片可绕对称轴扭转.在吸引质量作用下,检验质量钨片发生扭转振动,扭转位移通过电容位移传感器测量.实验未发现新的相互作用,排除了理论预言的strange和gluon moduli传递的相互作用的大部分参数空间,对于作用强度α=2000的dilaton,要求其作用程λ小于23µm,对于radion,要求其作用程λ小于88µm.

斯坦福大学Kapitulnik研究组[27,51,52]使用悬臂梁为弱力传感器,在低温下进行了非牛顿引力检验实验.他们在一大小为250µm×50µm×0.335µm的单晶硅悬臂梁末端粘上一长方体金块,悬臂梁的位移由光纤干涉仪测量得到,为了降低悬臂梁的热噪声,实验在10 K的低温下进行.吸引质量由相互平行的5列金条和5列硅条相互交替排列组成.由于金与硅的密度不同,通过选择适当幅度驱动吸引质量振动,他们将待测信号的频率调制到驱动频率的3倍频.此外,为了减小静电效应的干扰,在吸引质量与检验质量之间插入一块厚3µm的镀金氮化硅平板作为静电屏蔽膜.该系列实验最终给出了作用程在6—20µm范围内对非牛顿引力最强的限制.

印第安纳大学与普渡大学印第安纳波利斯联合分校Decca研究组采用微机械扭转振子(micro-electromechanical torsional oscillator,MTO)对微米间距的非牛顿引力进行了检验.2005年他们报道了测量一个镀金蓝宝石球和金-锗吸引质量间的相互作用力的实验[26],实验结果在λ∼200 nm处比之前国际最好水平提高了10倍.2016年,他们进一步将检验结果提高了约3个数量级.在新的实验中,他们使用气浮转台驱动吸引质量转动来进行密度调制实验[29].吸引质量为在硅片上半径不等的圆环“跑道”上制备的金-硅周期调制结构,结构重复个数从50至300不等.当驱动吸引质量转动时,检验质量的受力被调制到转动频率的50至300倍频,从而将待测信号与干扰信号在频域分离.实验选择气浮转台的驱动频率为ωd=ω0/n(n为金-硅结构重复个数,ω0为MTO的共振角频率),从而将待测信号调制到MTO的共振频率处,实现共振测量.该实验最终给出了作用程在40—8000 nm范围内新的限制,在λ=300 nm时比之前国际最好水平提高了1000倍.

由于微米间距实验主要的背景作用力之一为Casimir力,因此多个研究组通过对Casimir力的精确测量给出了此间距下对非牛顿引力的限制.如耶鲁大学Lamoreaux等[53]采用扭秤技术在0.7—7µm的间距通过测量镀金球面透镜和镀金平板之间的Casimir力给出了对非牛顿引力的限制.他们将实验数据扣除基于Drude模型的Casimir力理论计算值和静电力贡献后得到残差,将该残差作为非牛顿引力的上限,在0.4—4µm作用程给出了对非牛顿引力的限制,该结果比之前国际最好水平提高了30倍.加利福利亚大学河滨分校Mohideen等[54]采用悬臂梁作为弱力传感器测量了镀金球面和镀金平板之间的Casimir力.实验中补偿接触电势后,镀金球和镀金平板间的剩余电势产生的静电力在最近间距小于Casimir力的1%.实验测量结果与基于Plasma模型的Casimir力理论值在1%的误差范围内符合,综合考虑扣除Casimir力后的残差和实验误差,在1—150 nm范围给出了非牛顿引力作用强度的上限为1014—1018.

目前所有实验在其检验精度范围内均未发现牛顿反平方定律破缺,或存在新的非牛顿引力作用,仅给出了相应作用程非牛顿引力的上限.显然,图1所示的左下角参数空间还需更多更高精度的实验去检验.无论肯定与否,新的检验结果都将对引力物理、粒子物理和统一理论的发展具有重要意义.此前,华中科技大学引力中心采用精密扭秤技术,通过间距调制法进行了亚毫米和毫米间距的牛顿反平方定律的检验实验,并获得国际领先的实验结果.近年来,我们分别采用精密扭秤和原子力显微镜技术,在亚毫米和微米区间下,采用密度调制法检验反平方定律是否仍然成立[23,30],是否存在非牛顿引力.下面对这两个实验的进展进行重点介绍.

3 亚毫米范围检验牛顿反平方定律

我们分别在2007年与2012年完成了采用间距调制法在亚毫米与毫米范围的牛顿反平方定律检验实验[21,22],其特点是以两块正对的大密度平板为检验质量与吸引质量,利用精密扭秤测量其相互作用是否满足牛顿反平方定律.实验的优点是将待测效应最大化并集中在扭秤的灵敏方向,通过补偿设计抵消扭秤两端的牛顿引力,实现“零”检验,直接在实验精度下检验是否存在新效应.在更高精度的改进实验中,我们发现用于调制吸引质量间距的平移台会产生与待测信号同频的干扰.为了克服这一困难,在新的方案中[55],将吸引质量制作成多重对称的密度调制结构,把待测信号调制到驱动频率的8倍频.同时保留原实验的优点,测量正对钨片之间的法向力使待测效应最大化,并且通过“双补偿”设计将牛顿引力矩减小到扭秤的分辨率以下,改进静电屏蔽的措施进一步降低电磁干扰,实现“零”检验,最终给出更高精度的实验结果[23],本文对其进行详细介绍.

3.1 实验原理与装置

实验原理如图2所示,主要部件包括扭秤、角度探测与反馈控制单元、吸引质量及其驱动单元、静电屏蔽单元、引力标定单元.其中扭秤长90.74 mm、重60 g,呈左右对称,大小12 mm×14.63 mm、厚200µm的检验钨片粘贴在扭秤两端的玻璃基底前表面.吸引质量为8重对称结构,吸引钨片与补偿钨片交替分布,各部件中心到圆心的距离为38.8 mm,整体固定在精密转轴上,通过转台匀速驱动.待测效应为吸引钨片与检验钨片之间可能存在的非牛顿引力,其频率为驱动频率的8倍频,在频域与干扰信号有效地分开.由于在实验室尺度下宏观物体之间的引力作用非常微弱,各种环境扰动都会对实验产生严重影响,因此实验选择在山洞实验室进行,充分利用其天然的恒温、低震动、人类活动干扰少等优越条件.为了降低空气分子碰撞引起的噪声,扭秤与吸引质量安装在10−5Pa高真空容器中.扭秤通过长70 cm、直径25µm的钨丝悬挂,其偏转角用精度0.01角秒的电子自准直仪进行测量.由于扭秤与静电屏蔽膜的间距小,导体表面的残余电势会影响扭秤的稳定性,因此需要用静电反馈对扭秤进行控制,使它工作在稳定的位置上.吸引质量与转轴整体安装在六自由度操作台上,以调节吸引质量与扭秤的相对位置与姿态,实现“零”检验与“非零”实验的切换.实验过程中同步旋转一个质量与位置确定的引力源,对扭秤的灵敏度进行实时标定.

图2 实验方案示意图Fig.2.Schematic diagram of the experiments.

根据已有实验结果,在亚毫米范围内可能出现的破缺效应远小于牛顿引力,为了使实验结果可靠,我们使用“零”检验,即精确计算吸引质量对扭秤产生的牛顿引力,通过优化设计将其补偿到扭秤的噪声水平.通过求扭秤与吸引质量各部件之间的牛顿引力势对扭秤偏转角的偏导数,可得到引力矩

其中i表示扭秤各部件;j表示吸引质量各部件;ρ为密度;r=|ri−rj|为体积元dVi,dVj之间的距离,是扭秤偏转角θ与吸引质量转动的角度ϕ的函数.总力矩为所有力矩贡献之和,即τ(ϕ)= ∑ ijτij,利用数值积分计算吸引质量在不同转角ϕ下扭秤受到的牛顿引力矩τ(ϕ),再利用傅里叶级数展开求出实验关注的8倍频力矩分量.为了降低实验部件的几何误差要求,分别在扭秤与吸引质量上增加补偿质量,即“双补偿设计”,使扭秤在吸引质量转动过程中感受到的引力势几乎不变,从而在实验关注的频率上使牛顿力矩为零.另一方面,利用待测的破缺效应随间距增大呈e指数衰减的特性,设计时增大补偿质量的间距,使非牛顿引力不会被抵消.

实验主要针对Yukawa形式的破缺效应,对于特定的作用强度α与作用程λ,破缺力矩的计算方法与牛顿力矩类似,只需把积分中的牛顿引力势换成(1)式中的Yukawa势.为了方便数据处理,选取初始转角ϕ=0时,8倍频Yukawa力矩主要落在sin分量上,即

式中τY(ϕ)表示吸引质量在转角ϕ处对扭秤作用的Yukawa力矩,n表示转角次序.在后续的分析中称8倍频信号的sin分量为同相分量,cos分量为正交分量.

为了实现“零”检验,各部件严格按照设计要求进行加工与组装,其中检验钨片厚度误差0.4µm,相对扭秤中心的位置误差小于8µm,扭秤与吸引质量的整体定位精度好于7µm.另外,轴承转动过程中存在径向与轴向跳动,使吸引质量除了转动还有平动与晃动,从而对扭秤产生额外的引力误差.用红外位移探测器测量轴转动过程中沿x,y,z方向的抖动,以x方向为例,转轴抖动的峰-峰值约3µm,通过谱分析可发现存在高次谐波.提取实验关注的8倍频信号,其大小为(0.04±0.01)µm,相应的牛顿引力矩误差为(0.33±0.03)×10−17Nm.类似地,用自准直仪监测吸引质量转动过程中的晃动,θz方向8倍频分量为(0.11±0.23)µrad,可得到其贡献的牛顿力矩误差为(0.12±0.24)×10−17Nm.

根据扭秤与吸引质量各部件的实际测量尺寸、质量、位置、姿态、驱动精度等参数,可以计算出吸引质量作用到扭秤上的牛顿引力矩,在实验关注的8ω处为(0.72±0.50)×10−17Nm,其中与待测信号同相位的分量为0.72×10−17Nm,正交分量为−0.07×10−17Nm.同样可得16ω处牛顿力矩为(0.7±12.0)×10−17Nm,误差主要由吸引质量与扭秤的相对定位精度导致.

在良好接地的情况下,理想导体表面没有自由电荷分布.但由于不同材料的费米能级不同,会导致不同导体接触时存在接触势差,而且导体表面晶格取向、缺陷、杂质等因素,都会影响扭秤与吸引质量表面的电荷分布,从而产生干扰力矩[56].为减小静电干扰,对扭秤与吸引质量进行表面镀金,以及在吸引质量表面增加一层10µm厚的铍铜膜,使电荷分布更均匀.另外,还在扭秤与吸引质量之间插入30µm厚的屏蔽膜,并利用合金铝屏蔽罩对吸引质量及转轴进行全封闭屏蔽,以隔离吸引质量的电荷对扭秤的直接作用.实验过程中对扭秤与屏蔽膜之间的电势差进行高精度测量与补偿,平均电势的补偿精度优于1 mV.

3.2 闭环扭秤系统及其力矩噪声

实验中扭秤到屏蔽膜的间距只有200µm,近距离下残余电荷的作用使扭秤处于不稳定状态,需要通过电容极板进行比例-积分-微分控制(proportional-integral-differential feedback,PID),使扭秤偏转角基本保持不动,即工作在闭环状态.为得到控制电压对扭秤产生的力矩,以周期Tc=400 s连续转动一个铜柱作为引力源来标定扭秤的灵敏度.通过选择合适的初始转角,使标定信号的相位ϕc=0,则运动方程为

其中τccos(ωct)是待测的标定力矩,扭丝回复系数k=(8.05±0.06)×10−9Nm/rad,系统品质因数Q=(2552±1),根据几何与质量参数计算得到扭秤的转动惯量I=(6.977 ± 0.002)× 10−5kg·m2.从测量数据拟合出标定频率处扭秤偏转角的幅值θc,可得对应的引力标定信号大小为τc=(65.6±2.1)×10−17Nm.

在反馈控制状态下,闭环扭秤系统的运动方程为

其中ke为正对扭秤的屏蔽膜表面电势导致的等效负刚度,β是控制电压与力矩之间的系数.根据扭秤偏转角θ计算PID控制电压比例、积分、微分项的控制参数kp,ki,kd根据实验状态设定.另外两个待定参数ke和β则根据闭环系统对引力标定信号的响应求出,

根据闭环系统的传递函数,记录反馈控制电压,可求出作用到扭秤上的力矩,再提取关注频率上的待测信号.

扭秤非常灵敏,容易受到各种因素的干扰,通过选择良好的实验环境,采取高真空、恒温、隔震、电磁屏蔽等措施,可以有效地降低大部分干扰.当外部干扰降到足够低的水平时,扭秤的力矩噪声会达到热噪声极限.在高真空下扭秤的阻尼主要源于扭丝的内部耗散,称为结构阻尼,根据涨落耗散定理,扭秤热噪声的力矩功率谱密度为[57]

式中kB是玻尔兹曼常数,T是环境温度.结构阻尼的特点是其力矩噪声功率密度与频率成反比,在高频处力矩热噪声更小.另一方面,由于惯性作用,扭秤在高频处的角位移响应非常小,此时角度探测噪声成了最主要的噪声源.实验测得闭环扭秤系统的力矩功率谱密度如图3所示,在mHz附近接近热噪声极限,高频处受限于自准直仪的角度探测噪声,中间的峰是引力标定信号.实验时将待测信号频率设定到噪声最低的位置上.

图3 闭环扭秤的力矩噪声功率谱密度Fig.3.Power spectrum density of the torque acting on the torsion balance.

3.3 静电屏蔽膜的干扰

为降低静电干扰,通过源表在屏蔽膜上施加电压来补偿它与扭秤之间的残余电势.但实验表明,补偿后仍然存在较大的静电作用,原因是电荷的空间分布有涨落,施加固定的电压无法同时补偿表面各处的势差[58,59].检验钨片与屏蔽膜可以近似成平行板电容器,电容器面积S=(1.7537±0.0001)cm2为钨片面积,U为扭秤与膜之间的电势差,d为钨片表面到膜的间距,L=(38.04±0.01)mm为钨片中心到扭丝的距离,则检验质量钨片与屏蔽膜之间的静电作用力矩为

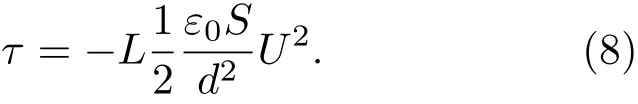
因此,无论电势差U的波动还是间距d的变化都会对扭秤产生变化的力矩,从而干扰实验结果.若电势差U随时间波动为∆U,则对扭秤产生的力矩波动为

实验中用源表补偿扭秤与屏蔽膜的电势差,其电压噪声小于10在实验间距下贡献的力矩噪声小于扭秤的本征噪声.当扭秤与屏蔽膜的间距变化δd时,扭秤受到的静电力矩的变化量为

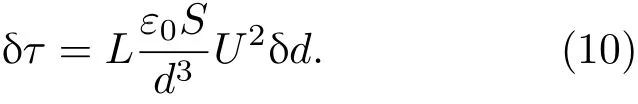
静电屏蔽膜稳定性引起的干扰力矩与扭秤到屏蔽膜间距d的立方成反比,与间距的波动量δd成正比,需要对其进行实验研究与排除.

实验采用一个表面平整的镀金玻璃圆盘代替真正的吸引质量,由于圆盘表面平整,在转动过程中不会对扭秤产生8ω的牛顿与非牛顿引力信号.但当用自准直仪测量屏蔽膜的晃动时,发现圆盘转动过程中膜的位置稳定性受到明显扰动,基频大小为(7.3±0.2)µrad,8倍频大小为(120±10)nrad,对应的间距波动约为5 nm.在此状态下测量扭秤的响应,发现明显的干扰信号,其中基频力矩τω=(45±22)×10−15Nm,8倍频τ8ω=(93± 45)×10−17Nm,比实验目标高了约2个量级.

静电屏蔽膜位置稳定性变差的原因是它与吸引质量驱动单元安装在同一个底盘上,转轴与转台不同轴导致转动过程中出现周期性变化的应力,使屏蔽膜产生微小运动.为此我们减小静电屏蔽膜与吸引质量的机械耦合,以及转轴与驱动转台之间的应力,膜的位置稳定性得到显著提高.重新驱动吸引质量旋转并监测膜的稳定性,晃动的基频信号降到(11±5)nrad,8倍频信号降到仪器噪声水平(1.7±1.8)nrad,改善近2个数量级,满足实验要求.在此状态下测试结果表明8倍频处未出现明显的干扰力矩,在2 mHz附近扭秤基本达到热噪声水平,积累5天数据表明8ω力矩结果为(1.4±1.6)×10−17Nm,主要受限于扭秤的随机噪声,延长测量时间可以进一步提高精度.从以上结果可以看出静电屏蔽膜的稳定性在近距离牛顿反平方定律检验中是一项非常关键的干扰因素,在高精度检验实验中必须给予足够的重视.

3.4 “非零”实验检验系统误差

根据“零”实验设计,吸引质量对扭秤的牛顿引力矩8倍频与16倍频分量在误差范围内接近零,但沿特定方向改变其相对位置后,8倍频与16倍频牛顿力矩会明显增大,利用这一变化规律可以检验实验装置是否存在系统误差.根据各部件的实际测量参数,可以计算出当吸引质量中心沿x轴错开时,作用到扭秤上的牛顿力矩变化如图4所示,图中上半部分是8倍频力矩,下半部分是16倍频力矩,灰色带宽表示考虑各参量的误差后理论上牛顿力矩的范围,其不确定度的置信水平均为2σ.同时,在相应位置上用扭秤测量到的力矩则是图中的黑点,可以发现实际测量结果与根据几何参量计算得到的牛顿力矩理论值在误差范围内符合,充分说明整套实验装置的设计与加工组装均与预期一致,各参量均满足实验要求.

图4 非“零”实验的8倍频与16倍频力矩与理论值比较Fig.4.Torques measured as a function of the displacement of the source mass along x-axis.

3.5 “零”实验结果

对于牛顿反平方定律Yukawa形式的破缺,当距离增大时破缺效应呈e指数衰减,对比不同间距的测量结果可以进一步提高实验的可靠性,为此分别在检验质量与吸引质量间距为295,695与1095µm下进行实验.由于实验需要极高的力矩分辨率,为了减小随机噪声,需要进行长时间数据积累,其中在295µm处积累了约80天数据,在695µm与1095µm处分别积累了约50天数据.间距为295µm的实验是检验非牛顿引力效应的主要实验,扣除残余牛顿力矩后,剩余的8倍频力矩为:

其中τin是与待测破缺信号相位相同的分量,τqu是其正交分量,误差的置信水平均为1σ;下标stat表示力矩的随机误差,下标syst表示系统误差,其主要来源是残余牛顿力矩误差.实验结果在95%置信水平下与零符合,即没有出现新的相互作用,牛顿反平方定律在此精度下仍然成立.

在间距295,695与1095µm下,扭秤测量的8倍频力矩扣除残余牛顿效应之后,结果如图5所示,图中圆点表示每5个吸引质量转动周期的分段数据提取出的力矩大小,方块是整组数据的平均值及其2σ误差,右下角的数据分别是正交分量与同相分量的中心值.可以看出,在2σ误差范围内,不同间距下的力矩测量结果均为零结果,并相互符合,充分说明在实验精度下没有出现牛顿反平方定律的破缺效应.

图5 不同间距下的实验结果Fig.5.In phase and quadrature components of the torques measured at different separations.

3.6 实验结果对Yukawa非牛顿引力的限制

实验采用扭秤与吸引质量间距为295µm处力矩的同相分量τin给出对牛顿反平方定律Yukawa形式破缺的限制.由于实验测得8倍频力矩为零结果,把测量结果作为Yukawa力矩τY的上限,可以得到作用程λ与作用强度α的关系为

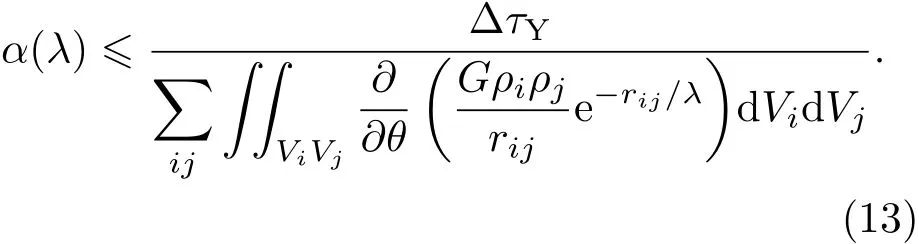
结合扭秤与吸引质量各部件的形状、位置、密度等参量可给出实验结果在不同的λ上对α的限制,从而绘出α-λ图.将测量结果的同相分量τin的中心值与误差按平方和合成,并取2σ,可得在95%的置信水平上Yukawa破缺力矩上限为

由此可以得到实验结果对Yukawa破缺的限制,如图6所示,图中右上角的浅色区域表示牛顿反平方定律仍然成立的区域,左下角空白区域是有待更高精度实验进行检验的区域.本实验未发现反平方定律破缺的信号,在λ为70—300µm区间给出国际上检验精度最高的限制,在λ>59µm的区间,实验允许的破缺强度|α|6 1.

图6 实验结果对Yukawa破缺限制的α-λ图Fig.6.Constraints on the Yukawa-type violation of ISL.

4 微米范围检验非牛顿引力

在微米及以下间距进行非牛顿引力实验检验面临着两个主要困难:1)当作用程一定时,非牛顿引力随间距呈e指数衰减,作用程越短,能够贡献非牛顿引力效应的体积越有限,非牛顿引力信号越弱;2)Casimir力和静电力的干扰越来越大,成为主要的背景相互作用.目前,此间距的众多检验通过精确测量Casimir力,然后从理论上扣除Casimir力和静电力理论值后给出对非牛顿引力的限制.然而,目前对Casimir力和静电力的理论计算仍存在争议[60],因此进行不依赖于Casimir力理论计算模型的实验检验将非常有意义.

4.1 实验原理与装置

在微米间距我们采用悬臂梁作为弱力传感器进行一个不依赖于Casimir力和静电力理论计算模型的实验检验[30,61],实验原理如图7(a)所示.检验质量探针为粘有金球的悬臂梁,该探针垂直于吸引质量表面放置,用于测量金球所受到的水平力的变化,而对垂直方向受力不灵敏,悬臂梁的位移由自制的光纤干涉仪[62]测量得到.吸引质量采用密度调制设计,即由大密度(金)和小密度(硅)的质量块相间组成,为了消除Casimir力和静电力的影响,在密度调制结构的表面蒸镀一层均匀、平整的金膜.当驱动吸引质量在y方向运动时,金球将受到一个周期变化的引力,其中牛顿引力比探针热噪声小很多,可直接忽略,如存在大于实验测量噪声水平的非牛顿引力将被实验探测到.

待检验效应为金球受到的非牛顿引力,可通过计算每个质量块与金球之间的力,然后叠加得到,即

其中ρj为第j块吸引质量块的密度,ρt为金球密度,r=|rt−rj|为金球体积元dVt与质量块体积元dVj之间的距离.

若在吸引质量表面(x,y)处,金球受力为F(x,y),当吸引质量以y0+Adcos(ωdt)做简谐运动时,金球将受到一个随时间变化的力,其在n倍频的贡献为:

其中f(x0,k)为F(x0,y)的傅里叶变换结果;(x0,y0)为吸引质量平衡位置;k=2π/Λ为空间角频率,Λ为密度调制周期;Ad为吸引质量的运动振幅;ωd为驱动角频率;Jn(kAd)为n阶贝塞尔函数;l为整数.由(16)和(17)式可知,n倍频信号与驱动信号或者同相,或者反相.综合考虑PZT位移台运动范围等因素,实验选择将非牛顿引力信号调制到8倍频,通过选择合适大小的驱动振幅Ad,可使8倍频处的非牛顿引力信号达到最大化.由(16)式可知8倍频信号随平衡位置y0周期变化,变化周期为密度调制周期Λ,因此可在一个调制周期内进行测量来检验是否存在非牛顿引力.

实验在一台超高真空扫描探针显微镜上进行,其真空系统由快速进样室、样品制备室和SPM室(scanning probe microscope,SPM)三部分组成,其中样品制备室与SPM室的真空度优于4×10−10mbar,样品制备室安装有离子枪、热蒸发源和样品加热台,可对样品进行离子束轰击、热蒸发镀金膜和真空退火等处理.整个平台支撑在四个气浮隔振腿上,用于隔离地面振动.SPM扫描头是实验核心测量装置,由三根弹簧悬挂安装在SPM室中,它由固定在钛框架上的探针单元、吸引质量及其驱动单元和激光干涉测距单元组成,如图7(b)所示.激光干涉测距单元中的聚焦探头安装在3个堆叠的纳米位移台上,可分别沿x,y,z轴运动,将激光聚焦到悬臂梁的反射板上,实现悬臂梁的位移测量.吸引质量驱动单元由6个纳米位移台层叠组装而成,自下而上依次为z,x,y步进位移台、xyz扫描位移台、y扫描位移台和倾斜调节台.3个步进位移台可实现吸引质量与检验质量相对位置的粗调节,xyz扫描位移台可以驱动吸引质量在x,y,z三个方向精细移动,实现扫描探针显微镜的功能.y扫描位移台为一大量程线性位移台,在室温下运动范围为80µm,用于驱动吸引质量做简谐运动.倾斜调节台可调节吸引质量绕x轴转动,使得吸引质量表面与y扫描位移台的运动轴平行,从而在吸引质量振动时保持检验质量与吸引质量间的距离不变.探针单元由插槽和固定在插片上的探针组成.针对不同的用途,设计了两种探针:ISL探针和q-plus探针.使用q-plus探针可实现原子力显微镜(atomic force microscopy,AFM)表面形貌成像;使用ISL探针可进行非牛顿引力实验检验,也可作为开尔文探针获得吸引质量表面的电势分布.

图7 (a)实验原理示意图,尺寸不成比列;(b)SPM扫描头设计图Fig.7.(a)Schematic diagram of the experiment,dimensions are not in scale;(b)design of the scanning probe microscope head.

金球与吸引质量间的间距采用隧道电流法设定,即将金球与吸引质量间隧道电流达到200 pA时的位置设置为“接触位置”,然后从“接触位置”通过xyz扫描位移台驱动吸引质量远离金球特定的距离来设定间距.金球到密度调制结构的总距离包括PZT驱动位移、间距设定过程中悬臂梁受力弯曲导致的位移修正、吸引质量表面金膜厚度和二氧化硅层的厚度.吸引质量表面与y扫描位移台运动轴的夹角可通过倾斜调节台控制到小于1 mrad.检验质量探针相对吸引质量的姿态在扫描头安装过程中进行了很好的控制.实验选择用正弦信号驱动吸引质量运动,驱动频率为2.1 Hz,振幅为18.44(16)µm.

4.2 检验质量探针与弱力测量噪声

检验质量金球采用氢氧焰熔融直径约10µm的高纯金丝制备,将其黏在氮化硅悬臂梁末端制成检验质量探针,图8为探针的扫描电子显微镜(scanning electron microscope,SEM)图.为了获得更小的悬臂梁弹性系数,采用聚焦离子束刻蚀(focused ion beam etching,FIBE)将购买的悬臂梁宽度减小,刻蚀后的悬臂梁柔性部分长76.6(4)µm,宽5.2(2)µm,反射板长27.2(3)µm,宽24.6(3)µm.金球半径为13.7(1)µm,在把金球从金丝切下时保留一段金丝用于操作金球,该段金丝长145(2)µm,直径为8.8(3)µm.为了将金球良好接地,探针传入样品制备室后,在正反两面各镀上20 nm厚的金导电层.

图8 检验质量探针SEM图Fig.8.SEM images of the assembly of the test mass and the cantilever.

悬臂梁的位移由光纤干涉仪测量得到,即y=SintVint,其中Sint为干涉仪的灵敏度系数,由干涉条纹曲线标定给出,Vint为干涉光强转化的电压信号.悬臂梁在外力驱动下的位移响应函数为

其中Fext(ω)为作用在探针上的外力.由于激光光场和悬臂梁的耦合作用,悬臂梁的共振频率和品质因数都会被光场改变,ωeff和Qeff为光力耦合作用下悬臂梁的有效共振频率和品质因数;为悬臂梁固有共振频率;keff为有效弹性系数;m为有效质量.通过测量悬臂梁一阶共振峰的ωeff,Qeff随激光光强的变化,然后外推出无光时可得到悬臂梁的固有共振频率f0=189.20(2)和固有品质因数Q0=319(7).由于待测信号频率为16.8 Hz,远小于悬臂梁的共振频率,因此悬臂梁的位移响应近似为y=Fext/keff,金球受力可由计算.

探针的有效弹性系数keff可通过测量探针位移谱给出.考虑探针结构复杂,我们根据SEM实测的探针尺寸,用有限元分析的方法计算了探针的振动传递函数,如图9中短虚线所示.通过唯一调节悬臂梁厚度参数,让计算得到的一阶和二阶振动的本征频率都与测量的共振频率在1%误差范围内符合,可得到探针的有效弹性系数keff=1.3(2)mN/m,采用的悬臂梁厚度参数为216 nm,比标称值(200 nm)略大.

图9 探针位移谱曲线Fig.9.The displacement spectral density of the cantilever.

探针弱力测量水平主要由两方面决定:探针热噪声和干涉仪位移测量噪声.在待测信号频率处,自制的激光干涉仪位移噪声本底为对应的力的测量噪声约为考虑光力耦合作用和悬臂梁的内部阻尼,探针的热噪声可表示为

其中ks为悬臂梁柔性部分弹性系数,由有限元分析计算得到ks=8.8(1)mN/m;Teff为光力耦合作用下探针的有效温度,可根据能量均分定理,由计算得到,其中ys为悬臂梁柔性部分末端的热激发振动位移.有效品质因数可通过拟合探针位移谱中的共振峰得到Qeff=112.根据获得的参数由(18)和(19)式计算得到图9中长虚线对应的理论热噪声曲线.图9显示:在待测信号频率处测力的总噪声为4.5约为光纤干涉仪噪声与探针热噪声贡献之和.

4.3 密度调制吸引质量

密度调制吸引质量由密度不同的金条和硅条组成,基于SOI(silicon on insulator)硅片制备.SOI硅片由3.3µm的器件层、400µm的体硅层和夹在之间60 nm厚的SiO2层组成,构成“三明治”结构.制备过程中,首先采用光刻技术和反应离子深刻蚀(deep reactive ion etching,DRIE)在器件层刻蚀出周期排列的槽,槽宽6.3(2)µm、深3.3(1)µm、周期12.2(3)µm,然后采用电镀法将沟槽填充金,形成金-硅密度调制结构,如图10(a)所示.将制备好的金-硅密度调制结构用紫外胶粘到石英玻璃块上,再采用机械研磨抛光和DRIE将体硅层刻蚀掉,露出平整的SiO2层表面.由于DRIE刻蚀Si和SiO2的速度比大于100:1,SiO2层作为刻蚀停止层保证了吸引质量的表面平整度.为了使表面电子性质均匀,吸引质量传入样品制备室后,首先用离子束轰击清洁表面,然后再在表面上蒸镀一层金膜.原子力显微镜测量结果显示制备的吸引质量表面随密度调制结构的平均起伏被控制在约3 nm,如图10(b)所示.

图10 (a)吸引质量SEM截面图;(b)吸引质量AFM表面形貌图(46µm×46µm)Fig.10.(a)SEM image of the source mass cross-section after electroplating;(b)AFM image taken on the source mass with 500 nm thick of gold coating and then thermal annealing.Image size:46µm×46µm.

4.4 Patch静电力干扰

在微米间距实验中,静电力是一项主要的实验干扰,由于吸引质量表面存在不均匀电荷分布(Patch电荷),静电力无法通过施加单一电压进行补偿,只能尽可能地制备电子性质均匀的吸引质量表面来减小该项干扰.图11(a)是检验质量-吸引质量间距为640 nm时测得的探针位移谱曲线,结果显示在驱动频率倍频处有信号峰.为了甄别这些信号的来源,在间距约为3µm时我们进行了以下对照实验:1)吸引质量静止,结果如图11(c)所示,在驱动频率倍频处未发现信号峰;2)驱动吸引质量振动,在基频和2倍频处出现干扰信号,未在其他倍频处发现信号,如图11(b)所示.基频和2倍频处的信号应该为吸引质量振动耦合到探针上引起,该信号随频率升高而衰减,未在更高倍频出现.通过对照实验,可推测在间距为640 nm时观测到的信号峰应与检验质量与吸引质量间的相互作用有关.

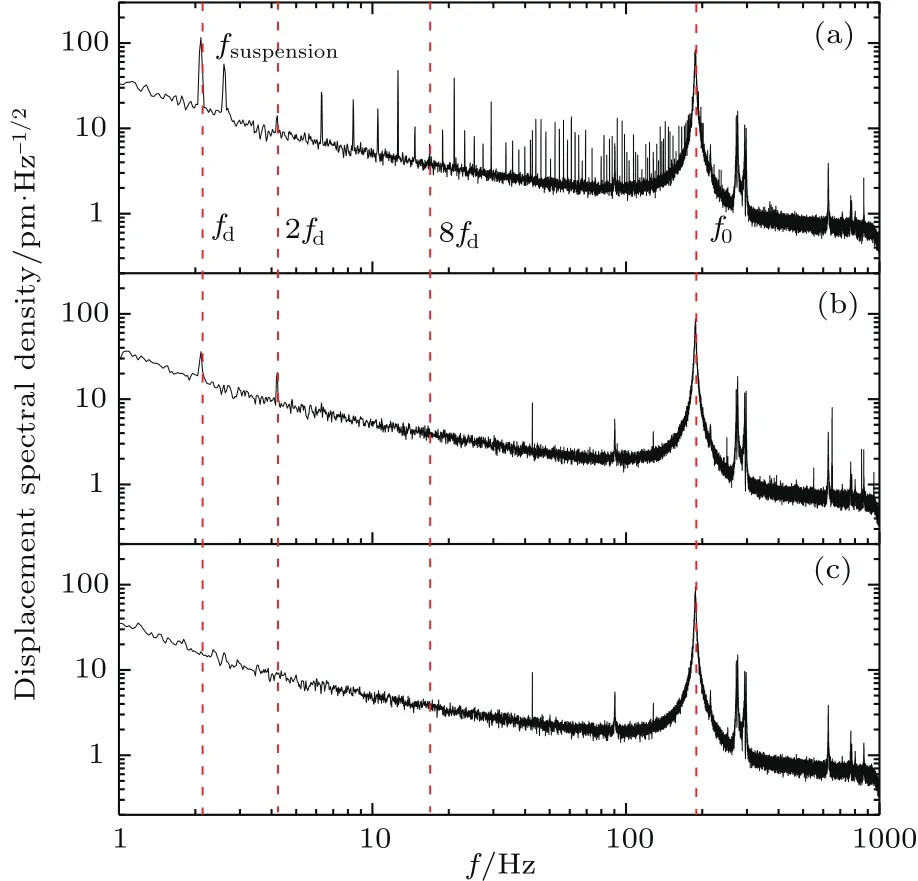
图11 探针位移谱密度曲线 (a)吸引质量运动,间距640 nm;(b)吸引质量运动,间距约3µm;(c)吸引质量静止Fig.11.The displacement spectral density when the source mass is(c)at rest,or oscillating at a distance of(b)∼3µm,(a)640 nm away from the test mass.

图12 金球到密度调制结构间距相同的情况下,不同金膜厚度和处理下测得的8倍频信号的二维分布图 (a)150 nm;(b)300 nm;(c)400 nm;(d)500 nm;(e)500 nm(150◦C退火12 h)Fig.12.2D maps of the force signal at 8fd.Thickness of gold coating:(a)150 nm;(b)300 nm;(c)400 nm;(d)500 nm;(e)the source mass is further annealed at 150◦C for 12 h.

为了进一步研究观测到的信号是由非牛顿引力还是其他干扰信号引起,我们测量了8倍频信号的二维分布图.测量方法为:保持检验质量与吸引质量间距不变,在二维平面内的不同平衡位置进行8倍频信号的测量,即驱动吸引质量相对该平衡位置振动,采集悬臂梁位移的时序信号,提取信号的8倍频振幅并转换成力信号,由此获得8倍频信号的二维分布图,如图12所示.

图12(a)为吸引质量表面镀金层为150 nm时获得的结果,可以看到8倍频信号呈条带分布,且条带的周期与密度调制周期一致,类似分布花样既可由非牛顿引力导致,也可由受调制结构影响的静电力导致.为了减小调制结构对表面电荷分布的影响,实验逐步增加表面镀金层的厚度至300,400和500 nm,并在保持金球到密度调制结构间距不变的情况下测量8倍频信号的二维分布图.实验发现随着金膜厚度的增加,8倍频信号分布与调制结构的相关性逐渐降低.由于金球到密度调制结构间距不变(905(54)µm),非牛顿引力效应大小不变,因此8倍频信号分布的改变应由静电力或表面电荷分布改变导致.虽然8倍频信号未再呈现明显的条带结构,但信号涨落大小基本未改变,其标准偏差分别为12.6 fN(150 nm),10.7 fN(300 nm),10.6 fN(400 nm)和12.5 fN(500 nm),说明表面电荷涨落的程度未改变.为了进一步减小表面电荷的不均匀分布,对金膜厚度为500 nm的吸引质量进行了退火处理,通过在150◦C退火12 h,8倍频信号趋于随机分布,随位置的涨落也减小为7.6 fN,如图12(e)所示.由此可见,随着金膜厚度的增加和后期的退火处理,8倍频信号趋于随机分布,且信号涨落减小,这些规律与由表面随机电荷分布导致的静电力影响预期是相符的.

此外,需指出的是本实验Casimir力的贡献远小于测量到的信号大小.对于实验测量的最小面间距354(38)nm,采用近邻力近似(proximity force approximation,PFA)估算理想导体间的Casimir力为0.76 fN,小于所测量的信号,而且实验发现8倍频信号涨落随间距的变化呈1/d0.6衰减,不符合Casimir力随间距变化的特性.以上结果表明Patch静电力可能为8倍频信号的主要来源,也是限制本实验检验精度的主要原因.下面将采用吸引质量退火处理后获得的静电力干扰最小的实验数据,在不进行Casimir力和静电力背景扣除的情况下,采用最似然估计法给出对非牛顿引力的限制.

4.5 实验结果对Yukawa型非牛顿引力的限制

为了充分利用二维分布数据中所有实验数据,可采用最似然估计法来给出对非牛顿引力的限制.对于二维图中每个格点对应的实验测量值,可以认为是对相互作用强度为α,作用程为λ的Yukawa力理论值的测量,假设其测量结果满足正则分布,则在吸引质量表面(xi,yi)处测量值为的概率可表示为

其中y00为理论与实验的位置偏置;总不确定度为,为力的测量不确定度,包括统计误差、探针的弹性系数误差、干涉仪灵敏度误差的贡献;为理论计算值的不确定度,主要由吸引质量与检验质量的尺寸、密度、相对角度、实验间距等测量误差导致的不确定度.对于相互作用强度为α,作用程为λ的Yukawa力,实验所测得的二维图与理论预期的二维图相似的条件概率为

其中A为归一化系数.

基于退火处理后获得的实验数据,计算得到概率分布函数P(y00,α,λ),如图13所示.理论与实验匹配最好时,相似概率最大,对应的α值为最似然值.对y00积分可得到相似概率随α的变化曲线,为获得95%置信水平下实验对非牛顿引力作用强度的限制,可计算总概率为95%时对应的α值范围的上限.对不同的λ值,均可分析得到95%置信水平的α值上限,由此可得到实验结果对Yukawa型非牛顿引力的限制,如图14中蓝色曲线所示.本实验获得的结果与Yale大学的Casimir实验结果相比,不需要进行Casimir力和静电力背景扣除,具有更高的可信度,该结果也是此间距下不依赖于Casimir力和静电力理论计算模型的两个结果之一.

图13 λ=1.0µm时,相似概率随α和y00的分布Fig.13.Probability function as a function of α and y00for λ =1 µm.

图14 实验结果对非牛顿引力限制的α-λ图Fig.14.Constraints on the Yukawa-type forces.The heavy solid line(blue)shows result from this work.

5 总结与展望

在近距离下对牛顿反平方定律进行高精度的实验检验有助于加深人们对引力的理解,并寻找可能存在的新相互作用.牛顿反平方定律的实验检验最早可追溯到1789年,至今已有很多研究组都对此进行了深入研究.华中科技大学引力中心长期从事这方面的研究,分别在毫米、亚毫米和微米范围进行了高精度的实验检验,2012年在毫米范围给出了对反平方定律破缺最强的限制.近年来,我们在亚毫米范围利用精密扭秤采用密度调制的方法,实现了当前最高精度的检验,实验结果未发现反平方定律的破缺信号,在作用程λ为70—300µm的区间给出了国际上最强的限制.在微米范围利用原子力显微镜采用悬臂梁作为弱力传感器,通过测量金球和密度调制结构吸引质量间水平力的变化来检验非牛顿引力是否存在,在95%的置信水平下给出了对Yukawa型非牛顿引力的限制,该实验结果不需要进行Casimir力和静电力背景扣除,具有更高的可信度.

至今,所有的实验检验都未发现牛顿反平方定律的破缺,或存在新的相互作用,实验结果仅给出了对相关理论参数的限制,新的参数空间的探索需要更高精度的实验检验.目前限制检验精度的一个重要因数来自静电力干扰,如在亚毫米范围实验中的屏蔽膜静电干扰,在微米间距实验中吸引质量表面Patch静电力干扰.要实现更高精度的实验检验,一般可从以下几个方面着手:增大检验质量与吸引质量的面积,从而增强待测的非牛顿引力信号;进一步压制各种干扰效应,比如亚毫米间距的牛顿引力效应、屏蔽膜静电干扰等,微米间距的背景Casimir力和Patch静电力干扰等;当干扰效应暂时不再是主要限制因素时,需提高力或力矩的测量精度,可选择进行低温实验降低热噪声,或采用新的技术,如光悬浮微球或利用光力学等精密测量技术.

在近距离下进行牛顿反平方定律的实验检验是华中科技大学引力中心众多师生和工作人员共同努力的成果,作者感谢他们的支持与贡献;作者感谢中国科学院理论物理研究所张元仲研究员、俄罗斯莫斯科大学Sternberg天文研究所Milyukov Vadim教授、美国加州大学Irvine分校Newman Riley教授、马里兰大学Paik Ho Jung教授、中国香港科技大学陈浩斌教授等的讨论与建议;感谢华中科技大学、物理学院的大力支持;感谢兄弟院校与同行专家的支持.