光和原子关联与量子计量∗

冯啸天 袁春华† 陈丽清‡ 陈洁菲 张可烨 张卫平

1)(华东师范大学物理与材料科学学院,上海 200241)

2)(上海交通大学物理与天文学院,李政道研究所,上海 200240)

1 引 言

计量的思想雏形最早源于度量衡的需求.随着人类文明的发展,科学体系与物理学的建立,对物理量的测量及单位标准的统一,逐步衍生出计量学.量子力学的诞生,进一步推动了科学与技术的发展,包括激光技术的发明、原子与分子物理学、量子光学及原子光学等科学分支的建立.这些新的科学分支与技术的发展又在原理与方法上为人们追求物理量的更高测量精度铺平了道路.在此基础上,量子物理与传统计量学自然结合,量子计量学(Quantum Metrology)应运兴起[1].相比于传统计量学,量子计量学结合量子物理,在微观层次探索与发展更精密的超越传统的测量方法与技术,同时研究量子力学不确定性原理对被测物理量施加的量子极限,以及怎样构建系统的量子态与测量方法实现被测物理量的最佳测量估值.在量子计量学的发展中,光子与原子及其光子-原子耦合体系扮演着十分重要的角色.例如光场的压缩态的产生与外差式探测,原子内部自旋态的制备,Ramsey干涉测量法及原子钟的发展,利用守恒量的对易性实现量子无损测量(quantum nondemolition),降低测量过程所引入的反作用噪声(back-action noise)等.随着量子光学与原子光学研究的不断深入与发展,光子与原子的量子特性正在逐渐向技术应用推进.在这个趋势里,光子作为信息的载体,原子作为信息处理的工具正在推动量子信息科学与技术的发展,而这一前沿发展又在量子测量的意义上刷新了量子计量学的内容.正因为如此,光和原子相互作用的量子耦合、量子关联特性,光子与原子体系的非线性多体效应等的研究已形成了一系列理论与实验结合的成果,为量子计量学打开了新的视野与研究窗口,进一步拓展了其理论研究与实际应用范围.

本文主要介绍光与原子关联特性及量子干涉研究的最新进展.第2部分简要回顾光学干涉仪发展的历史,并介绍线性干涉仪以及SU(1,1)型非线性干涉仪的结构、测量精度等;第3部分介绍线性光-原子混合干涉仪、非线性光-原子混合干涉仪的结构,分析这两种混合干涉仪的测量精度;最后是总结.

2 全光干涉仪

2.1 干涉仪的发展

在传统的计量学中,干涉法是最常用也是精度非常高的相位测量方法.马赫-曾德尔干涉仪(Mach-Zehnder interferometer,M-Z干涉仪)等线性全光干涉仪作为一种有效、通用的精密测量工具,自发明至今不断发展,取得了长足的进步,在表面诊断、天体物理、地震学、量子信息和精密测量等方面[2−12]被广泛应用.其中,激光干涉引力波天文台(Laser Interferometer Gravitational Wave Observatory,LIGO)运用激光干涉技术对引力波的成功探测[7,8]尤为引人瞩目.与此同时,人们也对干涉技术提出了更高的要求,以期实现更高的测量精度及更广的应用领域.

干涉仪本质上是通过相干地分束和合束各种波(光波[6−8]或实物粒子的德布罗意物质波[9−12])来实现相敏物理量的测量.因此,干涉技术的发展大致可归类为三类:一是改善干涉源的性质,即找到更合适的波源;二是改进波的分束合束过程,即找到更合适的分束器;三是找到更合适的信号探测方法.

针对干涉源的改进展,Caves[13]于1981年首次在理论上提出利用非经典光源(压缩态光场)能够提高光学干涉仪的灵敏度至散粒噪声(shotnoise limit,SNL)或标准量子极限(standard quantum limit,SQL)以下.Xiao等[14]以及Grangier等[15]后续实验实现了这一理论方案.此外,LIGO也通过注入压缩光源实现了Advanced LIGO在压缩频段灵敏度的进一步提高[16],且目前仍有理论研究利用纠缠光源进一步提升性能的可能[17]. 2000年,Boto等[18]提出用NOON态直接作为干涉仪的干涉臂,相位灵敏度可以达到海森伯极限(Heisenberg limit).2007年,Nagata等[19]实验制备了N为4的NOON态演示了这一类干涉仪,但是目前大N值的NOON态制备还存在诸多问题.

针对分束器的改进,1986年Yurke等[20]在理论上提出了一种新型非线性干涉仪,将传统M-Z干涉仪中的线性分束器换成了非线性分束器,原理上测量精度能够突破散粒噪声的限制,甚至逼近海森伯极限,这种干涉仪也称作SU(1,1)干涉仪.这一开创性的工作推动了此后非线性干涉仪相关理论和实验的发展,现今已经实验实现了全光SU(1,1)干涉仪[21]和原子SU(1,1)干涉仪[22],非线性干涉仪逐渐成为干涉仪领域的一个重要分支.

针对信号探测方法的改进,现今常用的探测方法有强度测量和零拍测量[23](homodyne detection,HD),近几年有人提出宇称测量[24−26](parity detection),还有一直以来量子计量领域普遍关注的量子无损测量[27].量子无损测量可以避免系统耦合以及探测过程中可能引入的反作用噪声,从而使最终的测量精度能突破标准量子极限.

光-原子混合干涉仪[28,29]是近两年发展的一种全新的干涉仪,将光和原子的拉曼散射[30]作为干涉仪的分束和合束过程,实现了光波和原子自旋波这两种不同类型波的干涉.通过选择合适的拉曼散射过程[31,32],已经实验实现了线性光-原子混合干涉仪和非线性光-原子混合干涉仪.值得注意的是,这种新型的混合干涉仪的两臂分别是光波和原子自旋波,因而最终干涉信号可以同时感受光场和原子自旋波的相位改变,相比传统的干涉仪拥有更广阔的应用前景.

2.2 线性全光干涉仪

1887年,Michelson和Morley[33]利用他们发明的干涉仪实现了对光场相位的精确测量,证明了以太不存在.这一干涉测量结果推进了爱因斯坦狭义相对论的发展,自此,干涉仪开始应用于精密测量领域.20世纪60年代初,随着激光的发明及应用,干涉技术实现了突飞猛进的发展,其应用范围也拓展至科学研究、工业加工检测、导航与精确制导等各个领域.本质上,任何引起干涉物质相位变化的待测量均可由相应的干涉仪进行测量.根据干涉物质的不同,干涉仪可以分为全光干涉仪和物质波干涉仪两大类.另外,根据干涉仪的分束器的种类又可以将干涉仪分为线性干涉仪和非线性干涉仪.

图1 M-Z干涉仪BS,光学分束器;Mirror,反射镜;PD,光电探测器;φ,干涉仪两臂的相位差Fig.1. Mach-Zehnder interferometer. BS,beamsplitter;PD,photoelectric detector;φ,phase shift between the two paths.

常见的全光线性干涉仪主要包括:M-Z干涉仪、Michelson干涉仪、Fizeau干涉仪以及Fabry-Perot干涉仪等.这里以M-Z干涉仪为例介绍全光线性干涉仪,其工作原理如图1所示.一束入射光场A与真空场B一起被50/50光学分束器分为两束,构成干涉仪的两条干涉臂A′和B′;A′和B′沿着不同的路径传播,并在第二个光学分束器上进行合束,合束后产生C和D.两条干涉臂在传播中会引入相位差φ.对于线性干涉仪,A,B,A′,B′,C,D,六个场的湮灭算符可以用来表示.假设50/50光束分束器是无损的,干涉仪的输入输出关系[30]:

干涉仪的相位灵敏度为

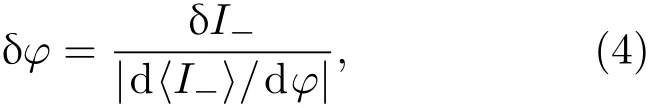
其中δI−代表探测信号的标准差.对于线性干涉仪,则有在φ = π/2处,相位测量不确定度最小,为这就是激光干涉仪相位测量的标准量子极限[34].

除了强度测量方案,平衡零拍探测[35]也是量子光学领域常用的探测方法.平衡零拍测量是对光场的正交分量进行探测,其中θ是本振光(local oscillation)相位,这里简化取θ=0.当C端口工作在暗条纹即φ=π时,一个待测的微小相移φs所引起的为

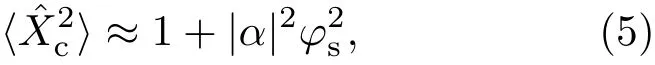
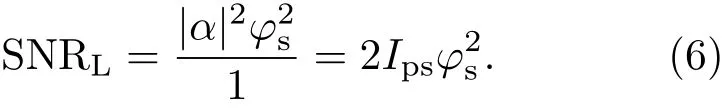
当SNRL=1时,也可以推导出标准量子极限其中N=|α|2.

为了突破标准量子极限,由(4)式可知,利用噪声低于散粒噪声极限的压缩光源,能够进一步提升干涉仪的测量精度,这一方案的相位灵敏度理论极限为1/N3/4[36].Xiao等以及Grangier等先后实验实现了3.0 dB[14]和2.0 dB[15]的干涉仪SNR提升.压缩光源也被应用在引力波测量中,Kimble等[37]理论上提出用压缩光作为引力波干涉仪的输入场,使其测量精度突破量子极限,从而提升引力波探测的能力.2013年,这一理论方案被实验证实,干涉信号在低频区域实现了2.2 dB的噪声压缩[16].

线性原子干涉仪于1991年首次在实验上实现[38−40],其结构与线性全光干涉仪一样,均可用图1表示.其入射端A,干涉臂A′和B′以及干涉输出端C和D均为原子波,原子波的分束和合束过程通常采用受激拉曼散射过程.原子干涉仪很快被广泛应用于各种原子相位所敏感的物理量的测量中[41,42],如测量地球旋转角速度、万有引力常数G[2]以及重力常数g[3]等.

2.3 SU(1,1)非线性全光干涉仪

前面所述的线性干涉仪的分束和合束过程都是通过线性分束器来实现的,在分合束过程中,波的总能量不增加.在不改变干涉仪装置结构的前提下,可以采用量子态来降低干涉仪的噪声,提高信噪比和相位灵敏度.除此以外,1986年Yurke等[20]提出了另一种方案,通过改变干涉仪的结构来增强干涉信号强度,从而达到提升测量信噪比和灵敏度的目的.具体而言,利用参量放大过程替代线性分束器,参量过程产生的两个干涉臂之间有量子关联,在合束过程中量子关联能够放大干涉信号的强度,从而增强相位灵敏度.传统的全光线性M-Z干涉仪,两个分束器可以用第二类特殊幺正群(SU(2))来描述;而对这一全新的非线性干涉仪,参量放大过程产生关联的双模光场,其产生湮灭算符构造的一组厄米算符的对易关系满足SU(1,1)群的性质,因而称之为SU(1,1)干涉仪.

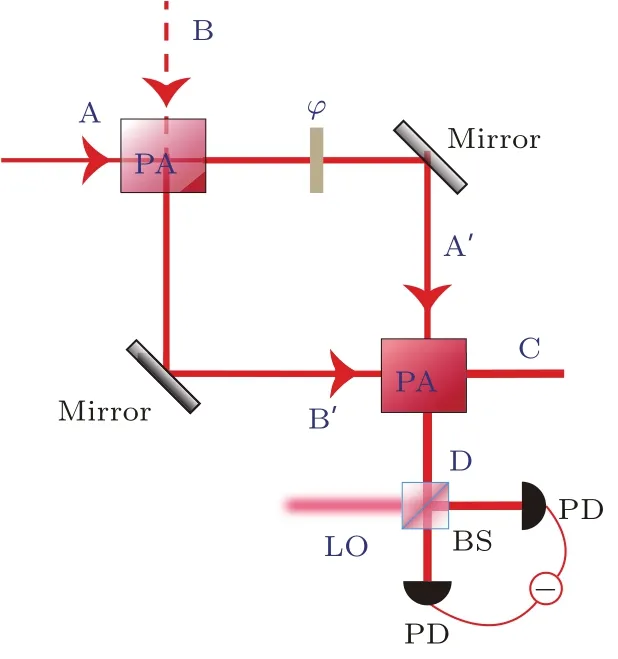
图2 基于参量放大过程的SU(1,1)干涉仪PA为参量放大器Fig.2.Scheme of an SU(1,1)interferometer with parametric amplifier process.PA,parametric amplifier.

文献[20]中提出实现SU(1,1)干涉仪的分束和合束过程哈密顿量为

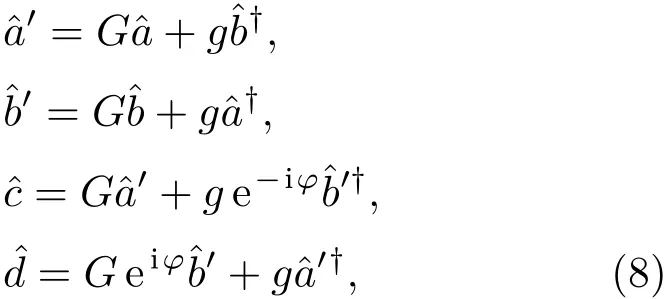
其中G和g为参量放大器的增益,G2−g2=1,φ为第一次参量放大过程后,干涉仪内部两路径带来的相位差.干涉仪的输入输出关系为

其中GT(φ)=G2eiφ+g2,gT(φ)=Gg eiφ+Gg.当端口A为相干态|α注入,B端口为真空态时,容易得到输出端C和D的信号强度(|α|2≫1)为:

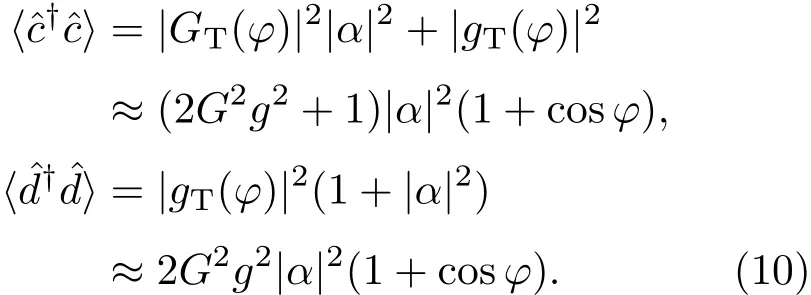
由(11)式可知非线性干涉仪的信噪比SNRNL=同线性M-Z干涉仪相比提升了2G2倍.需要注意,这里干涉仪其中一个输入端同样为真空注入,由于两个干涉臂之间的量子关联,两个参量放大过程中整体噪声没有放大,最终的干涉仪噪声仍为初始入射场的噪声.由此可知,SU(1,1)干涉仪相位灵敏度的提高主要来源于信号强度的增大,而非干涉仪整体噪声的压制.如果在非线性干涉仪的端口B输入压缩真空态,此时平衡零拍探测的信号即注入真空压缩态可以进一步提高非线性干涉仪的相位灵敏度.

2014年,利用四波混频过程作为参量放大器替代传统光学分束器的SU(1,1)干涉仪方案,在Rb85热原子系综中得以实现[21].如图3所示,其中(a)和(b)分别是SU(1,1)干涉仪和M-Z干涉仪的示意图,两种干涉仪的输入端同为相干态光场和真空注入,其相敏一臂的场强分别为和,控制参数使得此时对比两者的干涉条纹,SU(1,1)干涉仪相比M-Z干涉仪有5.5倍(7.4 dB)的幅度提升,如图3(c)所示.

2018年,利用同样的系统,Du等[43]测量了此类SU(1,1)干涉仪的信噪比.图4(a)给出了利用零拍探测测得的干涉仪输出端的噪声情况,黑线为散粒噪声水平,黄线为单次参量增益时(两个FWM过程只发生一次)的噪声水平,蓝线代表两次参量增益的噪声水平,红线为扫描干涉仪一臂的相位得到的噪声谱.理论上红线的最小值应该同散粒噪声的强度相等,然而实验中不可避免的损耗及其他非理想条件抬高了实际的噪声水平.尽管如此,干涉仪仍能在某些相位处获得相比单次增益更低的噪声.通过对干涉仪一臂施加一定强度的相位调制,实验首次测量了此类干涉仪的信噪比,结果如图4(b)所示.在相同的相敏信号强度下,SU(1,1)干涉仪的信噪比相比M-Z干涉仪提升了3 dB.

图3 两类干涉仪的示意图及其干涉图样[21] (a)基于四波混频过程的SU(1,1)干涉仪;(b)M-Z干涉仪;(c)等干涉臂场强条件下两者的干涉条纹,红线代表M-Z干涉仪;蓝线代表SU(1,1)干涉仪Fig.3.Schematic diagram and interference patterns for two types of interferometers[21].(a)FWM-based SU(1,1)interferometer;(b)M-Z interferometer;(c)the interference fringes of SU(1,1)interferometer(blue)and M-Z interferometer(red)with the same phase-sensing intensity.

图4 (a)基于四波混频过程的SU(1,1)干涉仪的噪声水平;(b)两类干涉仪的最小可测量相移φs随相敏光强Ips的关系图[43]Fig.4.(a)Noise performance for the FWM-based SU(1,1)interferometer;(b)the minimum detectable phase shift φsversus the phase-sensing intensity Ipsfor the M-Z and SU(1,1)interferometers[43].

3 光-原子混合干涉仪

光-原子混合干涉仪是一种新型的干涉仪,它以光和原子相互作用过程作为干涉仪中的分束器,相互作用过程所产生的光场和原子自旋波[32]作为干涉仪的两个干涉臂,光场和原子经过一段时间的演化再经过第二次光和原子相互作用进行合束,最终的干涉信号既对光场相位敏感也对原子相位敏感.这类干涉仪集全光干涉仪和原子干涉仪的优点于一体,能够应用于测量多种相位敏感的物理量,非常方便.与全光干涉仪和原子干涉仪类似,根据不同的分束过程,可以构建线性光-原子混合干涉仪,也可以构建SU(1,1)光-原子混合干涉仪.本质上,光和原子相互作用过程是实现光-原子混合干涉仪的核心.原子系综的拉曼散射过程是最常见的操控光和原子的手段[31,32],2015年和2016年,基于线性拉曼转换过程以及参量型拉曼放大过程,在实验上分别实现了线性光-原子混合干涉仪[28]以及SU(1,1)光-原子混合干涉仪[29].

3.1 线性光-原子混合干涉仪

其中η=geggem/∆,geg和gem分别是激发态|e与基态|g和|m的耦合系数.斯托克斯光场和拉曼写光场满足双光子共振条件ωW−ωS=ωmg,其单光子失谐均为∆.如果斯托克斯光场是一束非常强的相干光场,那么可以用经典量AS代替,得到

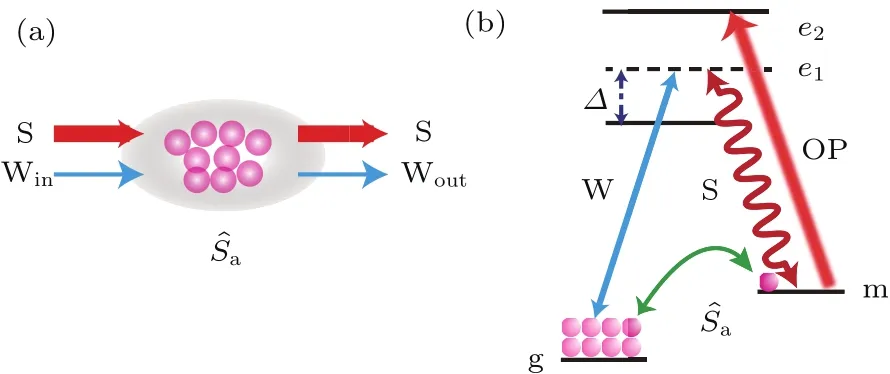
图5 (a)原子系综中的拉曼散射过程;(b)原子能级及光场Fig.5. (a)Raman scattering in an atomic ensemble;(b)atomic levels and light fields.

其中Ω≡2ηAS为拉比频率.在拉曼转换过程后,光场与原子自旋波可以写成:

其中θ=|Ω|t,t是演化时间;这是典型的线性转换过程,光场与原子自旋波之间发生线性的相干转换,(14)式即拉曼转换过程的输入输出关系.转换过程后的光场和原子自旋波由初始入射波,以及θ共同决定.从(14)式可以看出,如果≠0,S=0,或者≠0,=0,那么当θ=π/2时,拉曼转换过程后两个输出场的强度相等.以这一拉曼过程作为光-原子混合干涉仪的分束过程,产生的光场和原子自旋波作为干涉仪的两个干涉臂,经过一定时间的演化,光场相位增加φl,原子相位增加φa,可以写成:

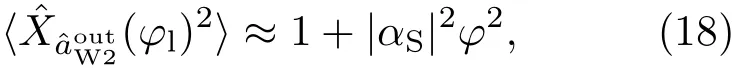
其中|αS|2为初始原子自旋波的强度,为相干态,满足αS= i|αS|. 由此可得干涉仪的信噪比这一结果同线性全光M-Z干涉仪类似,即线性光-原子混合干涉仪的灵敏度同样受标准量子极限的限制.

线性光-原子混合干涉仪的实验装置如图6所示,原子介质为Rb87原子,封在镀石蜡的圆柱形玻璃池中,原子池长50 mm,直径10 mm.实验中所用光场均为脉冲形式,使用声光调制器(AOM)实现光场的开断,抽运光脉冲宽度约为49µs,其他的光脉冲宽度均为100 ns;干涉仪分束和合束过程之间的延时约为500 ns,通过150 m长的单模光纤延时实现,其余相邻过程之间的光脉冲延时均为100 ns.整个光-原子混合干涉仪的实验分六步完成:第一步,初态制备,即通过光抽运让原子尽可能多的布居在|g态;第二步,干涉仪输入端的初始原子自旋波的制备,通过受激拉曼散射过程,在原子系综中制备出一定强度的原子自旋波Sa0;第三步,光和原子的分束过程,向原子系综注入强斯托克斯光场S1与原子发生第一次光和原子拉曼转换过程,通过控制实验参数使得θ=π/2,实现Sa0的50/50相干分束,产生的光场W1和原子自旋波Sa1作为干涉仪的两个干涉臂,原子自旋波留在原子池中,光场离开原子以光速传播;第四步,相位演化,通过改变光场W1的光程来改变光场相位;通过向原子中注入一个远失谐的probe光场,产生斯塔克效应来改变原子自旋波的相位;第五步,光-原子合束过程,因为在实验中,分束后的光场W1以光速传播,而原子自旋波仍待在原子池中,为了实现干涉合束过程,实验中将延时后的W1与另一路强斯托克斯光场S2通过偏振分束器(PBS)合束,再原路返回至原子池中,与原子自旋波Sa2发生第二次拉曼转换过程;第六步,干涉信号的探测;干涉仪光场输出端信号可以用光电探测器D1测量,而原子输出端信号无法直接进行探测,通过再次向原子池中注入强的读光场S3将原子信息转换为W3光场实现测量.

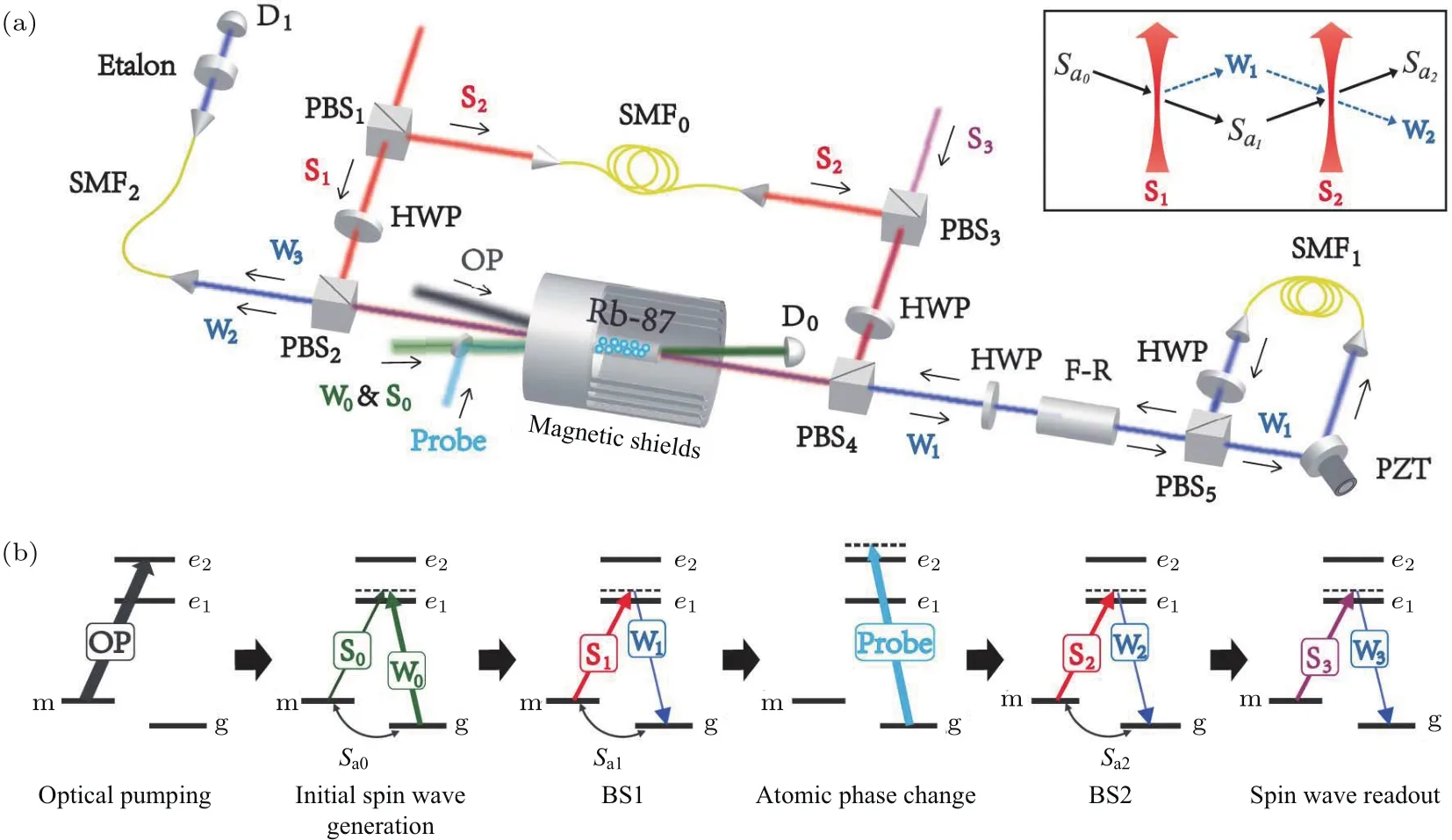
图6 线性光-原子混合干涉仪[28] (a)实验装置;(b)干涉仪流程图;所有光场均为脉冲形式,脉冲宽度及延时见正文Fig.6.Linear atom-light hybrid interferometer[28]:(a)Experimental setup;(b)process schematic.All the light if elds are pulses,whose widths and delay times are given in the main text.

图7 线性光-原子混合干涉仪的干涉图样[28] (a)扫描光场相位的干涉图样,蓝色实心方块为光场输出端,绿色点为原子输出端;(b)交流斯塔克效应改变原子相位的干涉图样Fig.7.Interference fringes of linear atom–light hybrid interferometer[28]:(a)Observed interference fringes for the optical fields(blue squares)and for the final atomic spin wave(green dots);(b)AC Stark effect on interference output.

线性光-原子混合干涉仪的实验结果如图7所示.图7(a)为改变光场相位的干涉结果.原子相位对磁场非常敏感,通过在原子池外围加磁屏蔽筒来屏蔽外界磁场的干扰、稳定原子相位.通过压电陶瓷对光场W1的光程进行周期扫描,横坐标是压电陶瓷的扫描时间,其正比于光程改变量,也就是光场相位改变量;纵坐标为合束后光场输出端的强度以及原子转换光场W3的强度.可以看出随着光场相位的改变,最终两个干涉输出端都呈现非常好的干涉图样,干涉对比度达到95%.原子输出端强度约为光场输出端强度的1/4,这是由原子转换过程中的损耗引起的,转换效率为25%.图7(b)给出的是改变原子相位的实验结果图,原子相位是通过向原子中注入一束远失谐的probe光场,利用交流斯塔克效应进行改变.斯塔克效应所引起的原子相位改变量为∆ΩAC=|µge|2I/2cε02∆,其中I 为probe光场强度,µge为偶极矩阵元,∆为probe光场失谐量.其中图中右侧的绿色三角波曲线为压电陶瓷扫描电压大小(用于改变光场相位),随着光场相位的扫描,干涉输出端呈现很好的干涉图样;褐色虚线为probe光场的开或者关,蓝色点为打开probe光场的干涉图样,红色点为关闭probe光场的干涉图样;两个干涉图样有一个明显的相位移动,两个干涉曲线之间的相位差就是原子相位的改变量.图7的实验结果直接反映了线性干涉仪的输出强度既随着光场相位而改变,也随着原子相位而改变,光场输出端与原子输出端强度互补,与理论预期一致.

3.2 非线性光-原子混合干涉仪

在线性光-原子混合干涉仪中,实现光和原子分束合束的拉曼转化过程是在强斯托克斯光场驱动下进行的,此时的相互作用哈密顿量,对应的是线性的相干转换过程.当拉曼写光场W光强较强可作为经典量AW处理,相互作用的哈密顿量:此时的哈密顿量与参量下转化或者四波混频过程的哈密顿量形式相同,为光和原子的类参量拉曼放大过程,从理论上说,产生的斯托克斯光场和原子自旋波为双模压缩态.基于此过程,就可以构建SU(1,1)型光-原子混合干涉仪,且最终的干涉信号的信噪比能够突破标准量子极限的限制.

Rb87原子的拉曼散射过程满足耦合方程:

将此过程作为非线性混合干涉仪的分束和合束过程,考虑如图8所示的SU(1,1)型光-原子混合干涉仪理论模型,第一次分束过程后,产生的光场和原子自旋波各自经历一相位变化,随后光场和原子自旋波空间合束,进行第二次参量型拉曼散射过程,最后得到干涉仪的输入输出关系:

为简化计算,假设干涉仪的注入场只有光场,Ia0≠0,ISa0=0,且对于两次拉曼过程,满足g1=g2=g,θ2−θ1=π,干涉仪输出端口的信号强度:

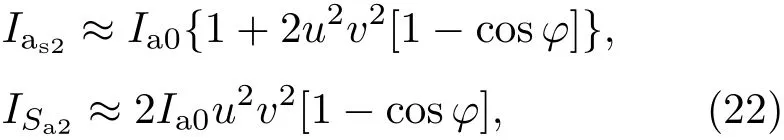
其中φ=φa+φl.由此可见,采用拉曼放大过程作为干涉仪的分束和合束过程,构建的非线性光-原子混合干涉仪,其干涉输出端口的强度相比于入射场强度有2u2v2的增益,并随着光场相位和原子相位的改变而改变,且两输出端口的信号同涨同落.光场输出端强度相比原子输出端强度多出一项入射光场项,因而其光场输出端干涉对比度略小于原子输出端.

图8 非线性光-原子混合干涉仪 (a)原理图;(b)拉曼放大过程中原子能级图,BS1和BS2分别表示干涉仪的分束和合束过程Fig.8. Nonlinear atom-light hybrid interferometer:(a)Theoretical scheme;(b)atomic levels and light fields in the Raman amplifier,BS1 and BS2 correspond to the wave-splitting and wave-combining processes in the interferometer.

非线性光-原子混合干涉仪的实验装置图如图9所示,两个拉曼放大过程作为混合干涉仪的分束和合束过程.干涉仪的实验实现过程为:1)光抽运,原子初态制备,与线性光-原子混合干涉仪一样;2)分束过程,一束强的拉曼抽运强光场W1与一束弱的斯托克斯光场S0发生第一次参量型拉曼散射,产生放大的光场S1和原子自旋波Sa1,光场S1和原子自旋波Sa1构成了混合干涉仪的两个干涉臂;3)干涉臂相位改变,在光场S1传播光路中可以通过压电陶瓷对光程进行改变,进而改变光场相位.原子自旋波在原子池中,可以通过给原子池区域加一个均匀磁场来改变原子相位;4)合束过程,光场和原子自旋波各自演化后,空间重合发生第二次拉曼散射,形成光和原子合束,产生最终的干涉信号S2和Sa2;5)干涉信号的探测,干涉光场输出信号S2可以用光电探测器直接探测,原子自旋波信号Sa2则需要用读光转换成另一束反斯托克斯光场AS进行探测.读取原子自旋波信号一般应该控制在原子的相干时间范围内,以减少原子自旋波的衰减.

图9 SU(1,1)型光-原子混合干涉仪实验装置图[29]Fig.9.Experimental setup of an SU(1,1)-type atomlight hybrid interferometer[29].

图10和图11给出了最终的干涉信号,其中图10为稳定原子相位,扫描光场干涉臂相位的实验结果.图10(a)对应初始入射波为斯托克斯光场的情形,S2是干涉光场输出端信号,AS代表原子自旋波输出端信号,实验上用另一束读光将原子自旋波转化为AS光场进行探测,读出效率大约为35%左右.斯托克斯光S2的干涉对比度是94.0%,AS光也就是原子自旋波的干涉对比度有96.4%,原子对比度比斯托克斯光高.若在第一次拉曼散射过程之前,在原子系综中制备原子自旋波(Sa0)作为初始入射波,最终的干涉信号如图10(b)所示,S2光场输出端干涉对比度是96.3%,AS光即原子自旋波端口的干涉对比度有93.6%.斯托克斯光的对比度比原子更高.无论是图10(a)还是图10(b),干涉仪的两个输出端的干涉信号同相.实验结果与理论预期相符.

图11(a)—(d)为稳定光场干涉臂相位、扫描原子相位的实验结果.光场相位通过萨格纳克环结构进行稳相,原子自旋波相位对磁场非常敏感.实验中,在磁屏蔽筒内加一螺线圈给原子加可控的均匀磁场,通过拉莫尔进动来改变原子内态的相位,相位改变的大小与磁场大小B和拉莫尔进动时间(这里主要由光学延时时间决定)T有关,ϕSa∝BT.在实验中,固定用于控制磁场的螺线圈电流扫描周期和扫描幅度,改变光纤长度(即T).图11(a)—(c)中光纤长度分别为60,100和160 m,最终输出信号呈现非常好的干涉图样,意味着原子自旋波的相位是随着扫描磁场B的大小线性变化的.不同光纤的长度,可以得到不同周期的干涉条纹.通过拟合不同延时情况下干涉仪的干涉信号,可以得到干涉信号的周期随光纤长度的变化,如图11(d)所示,呈线性变化趋势,在相同的磁场大小下,延时时间增大,相位线性增长,这与理论预期ϕSa∝ T 一致,斜率是0.0375 rad/(Gs·m).

图10 非线性光-原子混合干涉仪的干涉图样[29] (a)初始注入场为光场;(b)初始注入场为原子自旋波;红色的点是干涉仪光场输出端的信号,蓝色方格对应的是原子自旋波输出端的信号.为了方便直接比较两个输出信号,反斯托克斯光信号乘了3倍Fig.10.Interfering patterns of nonlinear atom-light interferometer with(a)initial injected optical field,(b)atomic spin wave.In both figures,the red circles are for the output signals and the blue squares are for the atomic spin wave(3 times magnified for comparison with the Stokes signal)[29].

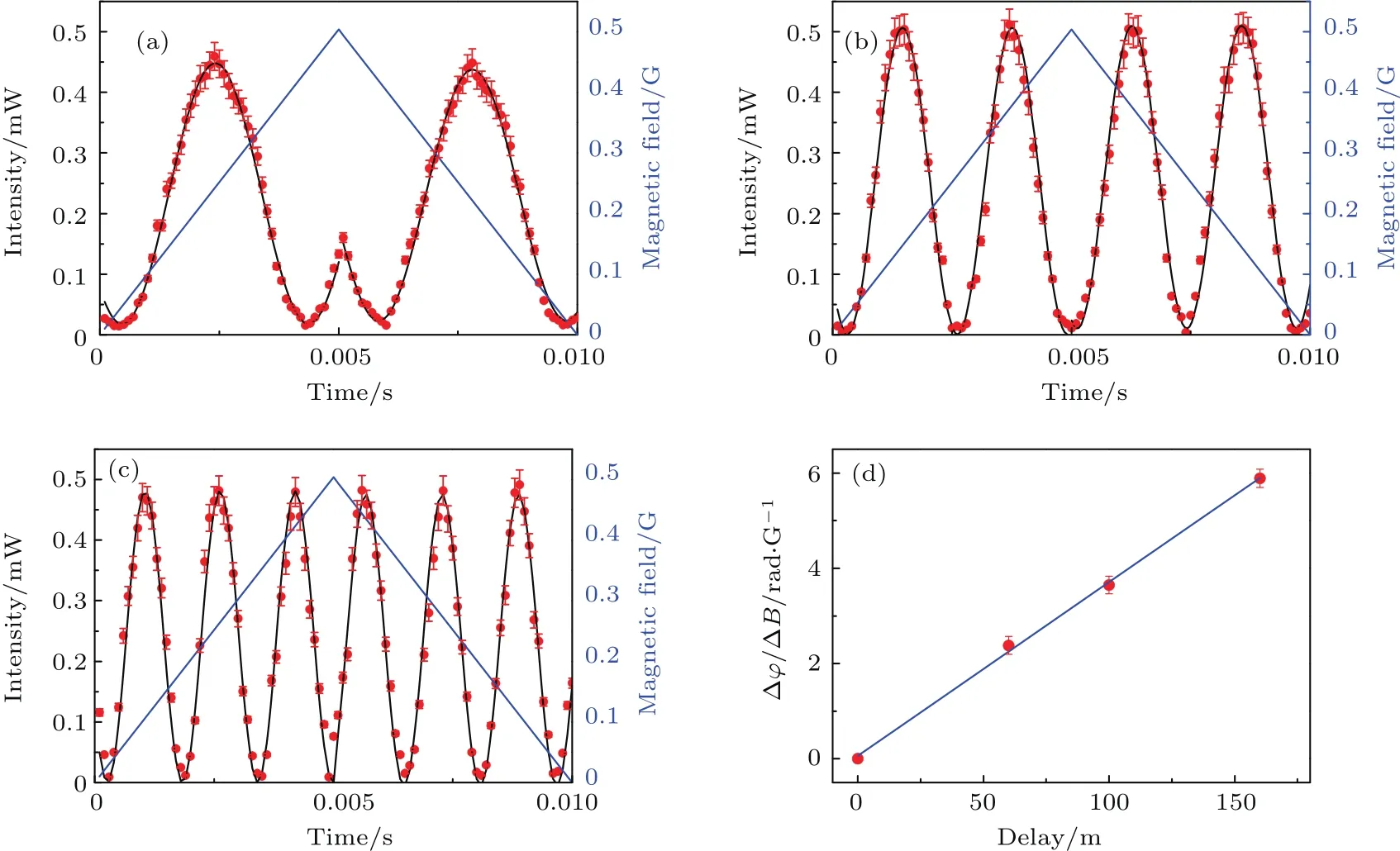
图11 通过磁场扫描原子相位得到的干涉条纹[29] 延时光纤的长度分别为(a)60 m,(b)100 m,(c)160 m;(d)相位灵敏度随延时光纤长度的改变;红色点为实验数据;黑线为干涉信号的拟合曲线;蓝线为扫描磁场的变化Fig.11.Interfering patterns with scanning atomic phase using different delay-time fibers:(a)60 m;(b)100 m;(c)160 m;(d)the relation between the length of fiber and phase sensitivity.Red dot,the experimental data;black line,the fitting curve of the interference fringe;blue line,the ramp scan of the magnetic field.(Ref.[29]).

从上述实验结果可以看出,非线性光-原子混合干涉仪具有既可以测量光场敏感的物理量(如距离),也可以测量原子相位敏感的物理量(如磁场、电场、光场等)的能力;与之相比,全光或者原子干涉仪则只能测量光场或者原子系统敏感的物理量.光-原子混合干涉仪综合了全光干涉仪和原子干涉仪的优点,在实际的应用中更加灵活.

3.3 光-原子混和干涉仪精度分析

干涉仪的相位灵敏度对于最终物理量的测量精度至关重要.特别是SU(1,1)型光-原子混合干涉仪,从物理原理上,两个干涉臂(斯托克斯光场和原子自旋波)之间具有量子关联特性,最终测量精度能够突破标准量子极限的限制[45].本节对干涉仪相位灵敏度进行分析,具体讨论平衡零拍探测(HD)和强度探测(ID)两种测量方案下的干涉相位灵敏度以及光场和原子损耗对相位灵敏度的影响.

根据(20)式中SU(1,1)型光-原子混合干涉仪的输入输出关系,若初始输入光场为相干光两干涉臂之间的相位差取为φ,采用平衡零拍探测,混合干涉仪输出的光场信号的正交分量为,干涉相位灵敏度∆φHD为

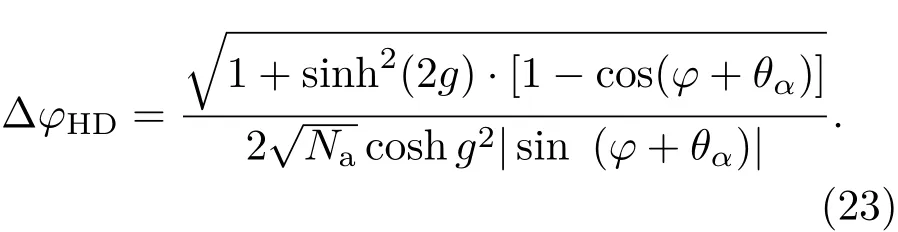
其中,∆ns2是输出光场的粒子数涨落.为实现最优的相位测量效果,灵敏度∆φ越小越好.对于零拍探测方案,我们发现相位灵敏度与θα有关,如图12(a),当θα= π/2时,在相位零点φ=0处可得到最好的相位灵敏度图12(b)对应θα=0,在相位零点φ=0附近处可得到最好的相位灵敏度,通过对θα进行控制可以获得最优的相位灵敏度.与零拍探测不同的是,强度探测得到的相位灵敏度∆φID仅与相移φ有关,图12(c)中在φ=0附近相位灵敏度最优.总体而言,平衡零拍测量得到的相位灵敏度要好于强度测量的结果.

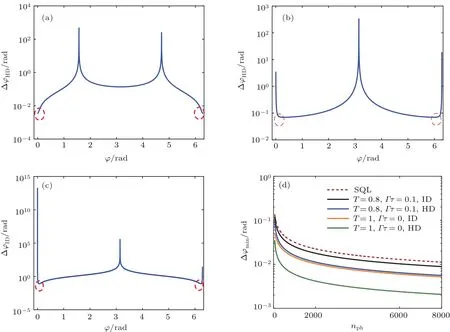
图12 (a)—(c)相位灵敏度∆φ随着相移φ的变化,(a)HD探测,θα=π/2,(b)HD探测,θα=0(c)ID探测;(d)最优的灵敏度∆φmin随着相敏粒子数nph的变化.参数取g=2,|α|=10Fig.12.(a)–(c)Phase sensitivity ∆φ versus the phase shift φ:(a)Homodyne detection,θα = π/2;(b)homodyne detection,θα =0;(c)intensity detection.(d)The best sensitivity∆φminvs the phase sensing probe number nph.Parameters:g=2,|α|=10.

干涉仪中的任何损耗都会引入额外噪声,进而带来测量精度的下降.考虑第一次拉曼散射过程后光场和原子在自由演化过程中引入损耗.将光场的损耗模拟成一个假想的线性光学分束器,斯托克斯光场ˆas1经历光场损耗演化成

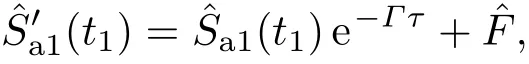
其中,e−Γτ为原子衰减因子,Γ表示基态的退相干率,远小于激发态的衰减率,

我们介绍了两种光-原子混合干涉仪,一种是采用拉曼转换过程作为干涉仪分束和合束过程的线性光-原子混合干涉仪,另一种是采用参量型拉曼散射过程作为干涉仪分束和合束过程的非线性光-原子混合干涉仪.两种干涉仪的干涉输出信号既对光场相位敏感也对原子相位敏感,可用于测量光场相位敏感的距离、位移、角速度等,也能够用于测量原子相位敏感的磁场、电场、光场等.光-原子混合干涉仪的可测物理参数广、应用灵活,且从原理上非线性光-原子混合干涉仪分束过程所产生的光场和原子之间具有很好的量子关联性,这种光子-原子量子关联干涉可用于探测原子量子态,提供突破量子极限的相位精密测量技术.

4 总 结

本文介绍了光和原子关联的产生以及相关的量子计量方面的最新进展,重点介绍了以原子中的四波混频过程为分束器的全光SU(1,1)干涉仪、以拉曼转换过程为分束器的线性光-原子混合干涉仪、以参量型拉曼散射过程为分束器的非线性光-原子混合干涉仪等新的干涉测量技术.这些基于光和原子关联的量子计量技术给量子精密测量领域提供了一些新的高精度测量方法.