基于元胞自动机的火灾场景行人流疏散仿真研究

金泽人， 阮 欣， 李 越

(同济大学 土木工程学院， 上海 200092)

人员的合理疏散方案对工程应急保障极为重要，突发情况下特定环境的人群疏散规律成为了近年来行人流研究的关注热点.考虑到进行大规模的实操演练费时费力，难以有效保证人员安全，因此人群疏散仿真模拟成为主流方法.人群疏散是基于个体选择的集体演化行为，主要受到个体的行为规律、个体之间的相互作用和个体与环境间交互的影响.如何较为准确地描述不同状态下个体的选择行为特征规律，是人群疏散模拟研究中的重点和难点.

针对这一问题，国内外主要发展了若干微观模型，从不同角度描述行人在疏散过程中的行为特点，模拟行人流的演化过程[1-6].基于元胞自动机(cellular automaton，CA)的场强模型(floor field)能够较好地反映行人的各项特征，物理概念明确，因此，在二维平面内描述行人流演化问题时得以广泛应用[1-2, 4].

目前，关于人群疏散的较多研究是针对大型场馆(如学校、体育场、地铁等)和多层建筑的疏散讨论[7-10].其中考虑了若干突发灾害导致的疏散情景，火灾是突发灾害中具有代表性的一类.在疏散模拟中，应当特别考虑行人在火灾环境下的行为特征.国内外采用CA模型研究火灾环境下的人群疏散问题时，主要通过下述方法考虑火灾影响.Yamamoto等[11]假设行人运动过程中始终与火灾蔓延范围保持大于某一定值，以确保行人的安全，但无法考虑随机因素的影响.Zheng等[12]将火灾产生的影响等效为场强，在场强模型中引入火灾对元胞选择概率的降低作用，但同样未考虑火灾引起的恐慌对行人的随机作用.杨立中等[13]在模拟中引入了危险度以考虑火灾对行人行为规律的影响，利用火灾和出口位置对某一元胞的潜在威胁评价当前行人的所受到的危险程度，并假定行人总是向最低危险度的方向移动，但是这样将行人视为完全理性的决策体，并不能充分反映火灾情况下的恐慌心理对行人选择的影响.吕春衫等[14]在模拟火灾环境的作用时采用了火灾动力学模拟器FDS(fire dynamic simulation)，引入健康度的概念以评估行人在疏散过程中的状态，并引入某一随机方向来描述行人在火灾下的紧张行为.然而，以随机方向考虑行人的紧张行为并不能很好地描述火灾对行人的总体排斥作用.

此外，上述研究主要采用均一化行人移动特征，认为行人始终按照给定的固定速度进行疏散，不考虑行人在疏散过程中移动速度的变化特性，并较少体现特定场景对行人疏散选择的随机影响.然而，在实际情况下，行人在疏散过程中将根据周围行人的密集程度调整自身的移动速度，不同场景下的行人的移动速度存在差异.考虑这一因素，已有的疏散模型均一化的移动特征不再成立，有必要进一步拓展.

基于上述分析，目前的研究在描述火灾环境中行人的应激行为时未充分考虑随机因素的影响及火灾方位和移动方向的关联性，难以体现疏散过程中行人速度的变化规律.针对上述问题，本文采用了已有文献中广泛应用的场强模型框架，在此基础上进行拓展，提出行人基于场景的移动方向和期望速度规则，并应用于火灾场景下行人流疏散模拟仿真.具体如下：在火灾场强的基础上，引入火灾场景下移动方向的改变规则，描述火灾对行人的心理作用，对基于转移概率的场强模型进行补充和修正；提出行人期望速度的概念，建立期望速度改变规则，以反映行人在周围行人流影响下对移动需求的调整；采用移动判定准则以描述行人移动速度的差异，实现了异步行人移动的演化；研究并分别讨论了火灾下移动方向和期望速度改变机制对系统疏散能力的影响规律，基于分析结果对实际的疏散过程给出建议.

1 基本地面场模型

1.1 基本CA模型

CA模型最早由Ulam和Neumann提出[15]，起初被用于“生命游戏”这一生命系统特有的自复制现象，是描述复杂演化现象的一种简化模型.模型中有限且连续的疏散平面被一定尺寸的网格划分为若干边界明确的二维元胞，各个元胞或被墙壁和障碍物占据、或被行人占据、或为空.网格的尺寸根据模拟的要求确定，在密集人流中，典型的人员空间分配可取每个元胞对应Δs×Δs=0.40 m×0.40 m[16]，每个元胞最多容纳一个行人并规定每个时间步长内行人只能移动一格.这些元胞中存储行人的移动参数或障碍物的占据参数.行人在一个时间步长内的移动范围为3×3的元胞区域，即为Moore型邻居，行人占据了移动区域的中心位置，如图 1a所示.行人根据元胞中预先设定好的规则，参考当前自身和Moore邻居内的元胞参数状态，按相等的时间间隔自行演化，使行人的移动参数在元胞间转移，如图 1b所示，实现行人在疏散平面中的位置变化.

ab

1.2 基于CA的场强模型

国内外研究提出了若干种基本CA模型的行人移动规则[5,17-18]，多种规则的差异性主要体现在公式的定义上，在物理概念上主要包括出口对行人的吸引、行人之间的相互排斥以及行人对环境的应激反应等基本特性.

基于CA的场强模型能够较为全面地考虑疏散过程中行人的上述基本特性.场强模型中，行人的疏散过程被离散化为相等的时间步长，在每个时间步长内，若行人满足移动判定条件，行人或移动至Moore邻居内的其余元胞，或原地等待.行人在允许移动的时间步长内会判断移动区域各个元胞的场强大小，并考虑其余行人的元胞占据和周围障碍物情况，得到移动区域内行人向其他元胞的转移概率pij，即

(1)

式中：静态场Sij表示基于距离的出口对行人的吸引作用；动态场Dij则通过参考其他行人走过的线路信息，描述行人间的从众行为；惯性场Iij是行人当前运动方向对后续移动偏好的影响；火灾场Fij表示火灾对行人的确定排斥作用；kS，kD和kF分别为其权重敏感系数，反映了不同场强对总场强的贡献大小，且有kS,kD,kF∈[0,∞)；nij和ξij分别表征了其余行人和障碍物的占据信息，若元胞处没有被其余行人占据，则nij=0，反之nij=1，若元胞处为障碍物，则ξij=0，反之ξij=1；N为概率的正规化处理，表达为

N=

(2)

静态场强Sij可描述为单位时间步长内与出口距离的减少量，应考虑垂直水平方向和斜线方向的行走长度不一致，可参考文献[19]进行计算.若疏散平面内存在障碍物分布，常用方法是采用基于Dijkstra算法计算各元胞位置与出口的距离[1].动态场强Dij描述了行人留下的虚拟路径信息对其余行人移动选择的影响，用以反映行人的从众行为，其中包含扩散系数α和消退系数δ，参考文献[5]进行计算.惯性场强Iij描述了行人的运动惯性，即在可移动范围内，与上一次运动方向相同的元胞位置处Iij=ω，ω>1，其余元胞处Iij=1.火灾场强Fij取决于元胞和火灾蔓延区域的最小距离H，参考文献[12]进行计算.

考虑到行人移动和冲突的随机性，当一个时间步长内有两个及以上的行人选择了相同的目标元胞时，则所有行人将以一定的概率μ保持静止[2].否则，选择一个行人进入该目标元胞，其余行人保持原地等待.

2 火灾场景下的疏散模型

2.1 基本火灾模型

在研究疏散环境时，可认为工程结构内的火灾由局部点引发，并且火灾在一定范围Rf(单位：元胞尺寸)内传播.火灾每隔Tf(单位：s-1)向周围扩散，每次扩散的增量为一格，假定被火灾蔓延区域覆盖的行人即死亡.火灾模型中，火灾的传播频率Tf是火灾传播范围Rf的函数，表达为

(3)

式中：Rm为火灾扩散极限范围，即当Rf=Rm时，火灾不再进一步蔓延.Rf和Rm的定义如图2所示.

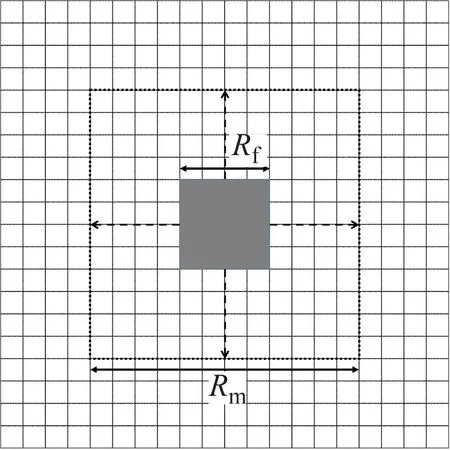
图2 火灾演化模型

2.2 基于火灾场景的移动方向

火灾场景下疏散区域内的行人移动规律具有特殊性，火灾对行人的影响体现在两方面：一方面，行人受到火灾的排斥，倾向于远离火灾蔓延区域，此时火灾和障碍物对行人的影响类似，下文将其描述为火灾的物理作用，在数学模型中通过火灾场强加以描述；另一方面，火灾的发展将直接影响行人的心理状态，这种影响和行人与火灾之间的相对距离有关，距离越近，行人下意识反向逃离的倾向就越为显著，下文将其描述为火灾的心理作用.

疏散环境中火灾将向所有非障碍物元胞蔓延，火灾蔓延区域内的元胞等效为障碍物，行人在疏散过程中不会主动进入火灾蔓延区域.

火灾的心理作用通过行人的恐慌程度及相应的移动方向间接表达.行人是否产生恐慌受到周围环境的影响，认为行人与火灾蔓延范围的距离越近，则产生恐慌的概率越大，并假设行人的镇静概率Pc是行人与火灾蔓延范围的函数，表达为

Pc=1-exp(-λ(H-1))

(4)

式中：λ为镇静概率增长系数，λ越大，Pc随H增长得越快，即行人在最小距离H相同时更为镇静，但均有H→∞时Pc→1.当H=1时，行人的镇静概率Pc=0，说明此时行人必然发生恐慌行为.如图 3a所示，Pc的增长速度随着H的增大而不断降低，说明随着最小距离的增大，火灾对行人的心理影响不断减小并最终趋于平稳.为进一步验证λ对行人疏散的影响，下文将对λ进行参数分析.

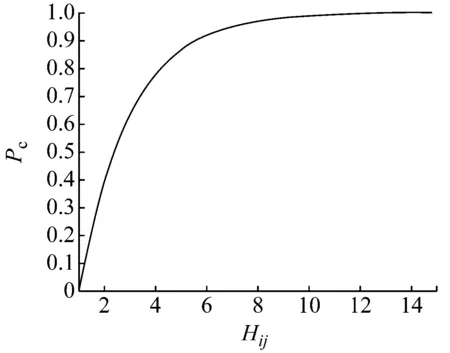
a λ=0.50

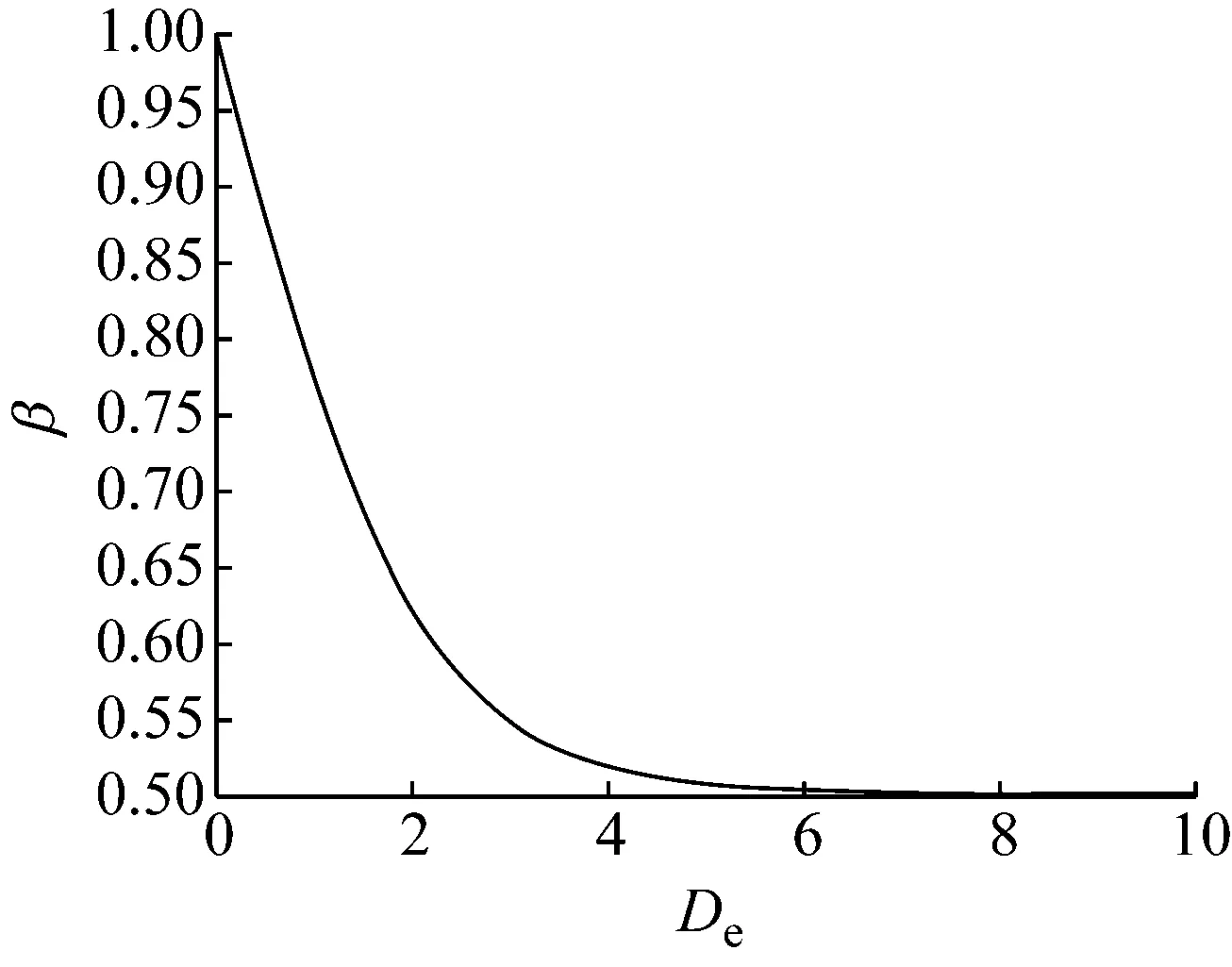
b γ=0.50

在行人疏散过程的每一时间步长内，根据其所在位置相应的镇静概率Pc，通过随机抽样的方法判断是否发生恐慌行为.若不发生恐慌行为，行人则继续场强理论(式(1))确定目标元胞.否则，计算行人所在元胞(i,j)与最近的火灾蔓延元胞(if,jf)的方向向量R=(i-if,j-jf)在移动区域内的8个不同方向上的投影值，取投影值最大的方向为行人移动方向.

在实际情况中，若行人处在火灾和障碍物形成的狭长通道中，其首要目标为尽快离开这一区域.此时，假定不考虑火灾对行人的物理作用和心理作用，行人将根据式(5)选择目标元胞，行人移动状态如图4所示.

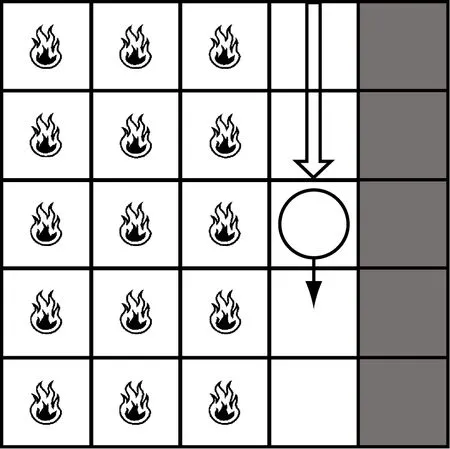
图4 行人在狭长通道的移动规则

pij=N exp(kSSij)exp(kDDij)Iij(1-nij)ξij

(5)

2.3 基于行人流场景的期望速度

行人在疏散过程中的行为与心理状态密切相关.目前大多数模型均假定行人的移动速度在整个疏散模拟过程中保持恒定，行人在各个时间步长内均能按转移概率进行移动选择.这一假定难以描述同一行人在不同情境下的速度选择特性.行人的实际速度Va应当是由受周边环境影响的行人主观移动需求和客观移动条件(周围行人和障碍物分布)共同决定的，称行人主观移动需求为该行人的“期望速度Ve”.行人会根据视野内的人数动态调整期望速度.当视野内不存在其他行人时，某一行人将采用最大的期望速度Vb(以下称为基本期望速度)；当视野内存在不同数量的行人时，某一行人为避免加剧前方的拥堵程度，将根据行人的密集程度，主动降低当前的期望速度，并定义β为期望速度折减系数，则行人在某一时刻的期望速度Ve=βVb.期望速度折减系数β表达为

(6)

式中：De为视野中的行人密度，单位为人·m-2；γ为期望速度折减系数下限，当De→∞时，β→γ.如图 3b所示，β的下降速度随着De增大而不断降低，说明随着视野内行人密度的增大，Ve将趋于平稳.为进一步验证γ对行人疏散的影响，后文将对γ进行参数分析.

行人的视野可用视角αs和视距rs确定的扇形表示，如图 5所示.行人的视野中心线方向为行人在上个时间步长内的移动方向.

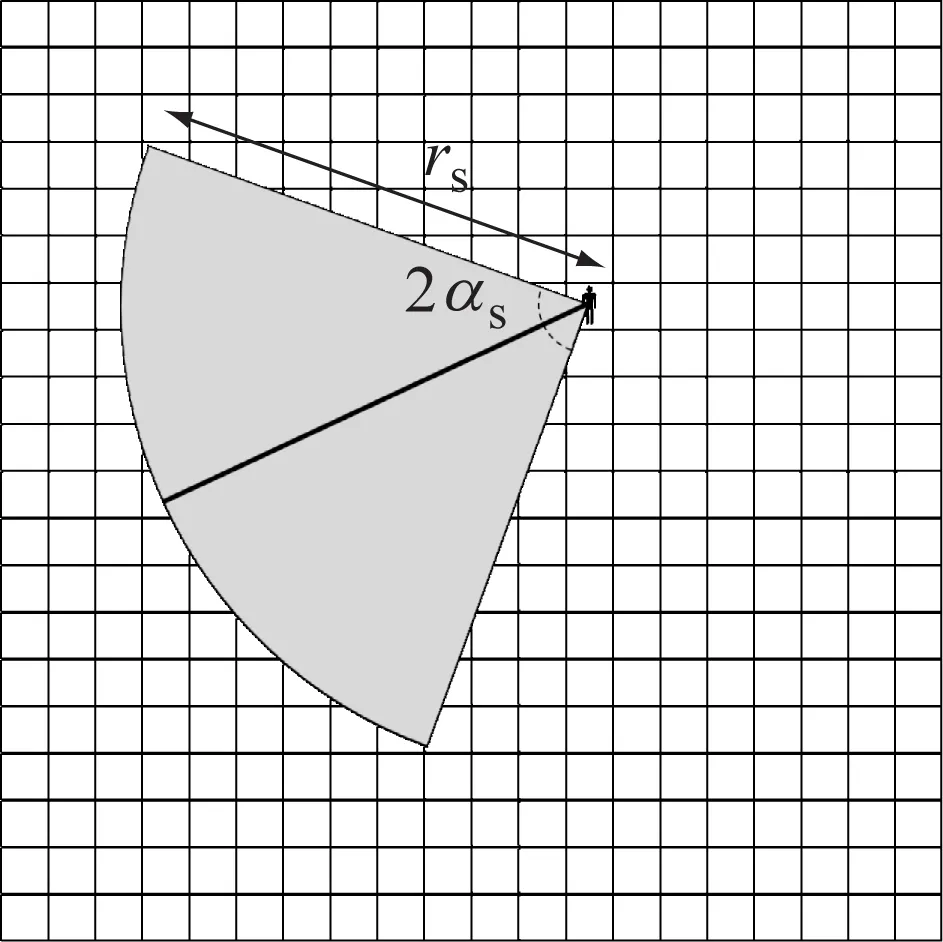
图5 行人视野示意图

为描述行人移动能力的差异性，模拟过程中采用移动判定准则确定某一时间步长内特定行人的移动状态.若满足移动判定准则，行人则可在时间步长内按转移概率进行移动，否则，该时间步长内行人保持静止.记模拟经过的时间为t，行人i的移动速度为Ve(i)，行人i上一次获得移动的时刻为Tm(i).

(1) 第一个时间步长内，允许所有行人按照转移概率进行移动.此后，移动判定准则如(2)～(3)所述：

(2) 若行人i在时刻t移动，则记Tm(i)=t；

(3) 若满足t≥Tm(i)+Δs/Ve(i)，则行人i在t时刻满足移动判定准则(Δs为元胞尺寸)；

(4) 满足移动判定准则的行人按照转移概率或基于火灾场景的移动方向进行移动.

2.4 火灾场景下人群疏散模拟流程

模拟开始时，首先建立疏散平面的物理环境，其中包括疏散平面的几何尺寸(空间形状和分布)、边界条件(出口宽度和出口位置)和障碍物分布，确定行人的疏散通道和目的地.根据给定的密度将行人随机布置于疏散平面中，并按照行人的类型和一定的分布随机赋予差异化的行人移动属性.

模拟过程中，主要分为两个功能模块：行人的移动模拟和火灾的演化模拟.

行人移动模拟包括场强的计算、行人移动方向的确定、行人期望速度的调整以及行人移动冲突的解决.场强的计算包括非时变的静态场强S和时变的动态场强D、火灾场强F和惯性场强I.静态场强S可在疏散平面物理环境建立后计算并应用于整个模拟过程，其余场强需要在各时间步长内迭代更新.行人移动能力包括在特定时刻的移动许可和期望速度的判定.行人移动方向是判定行人是否出现由火灾导致的恐慌行为.行人移动冲突时，按照前文所述的冲突解决准则进行处理.

火灾的演化模拟较为灵活，可根据特定的火灾环境和特点进行调整.其主要的参数包括火灾的发生点、传播速度、传播范围及火灾对行人的作用假定.

模拟过程中假定火灾的演化不受行人移动的影响，行人根据火灾环境下的场强强弱和移动方向进行疏散路径的选择.当所有行人死亡或离开疏散系统后模拟结束，得到疏散系统中剩余行人(含死亡行人)和死亡人数的时变曲线，并以此进行系统疏散能力和人员安全的评价.

基于上述设定，进行火灾场景下工程结构内人群疏散的模拟分析时主要遵循的模拟流程如图6所示.

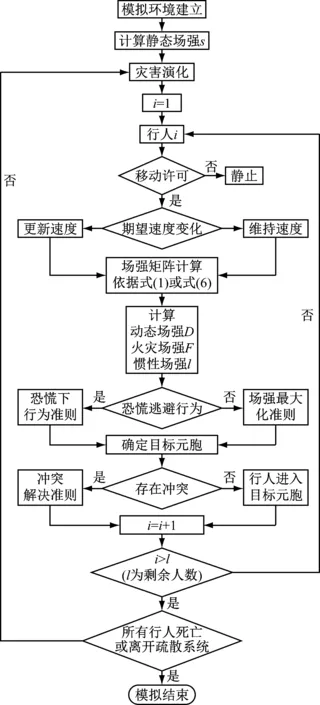
图6 火灾场景下工程结构内疏散模拟流程

3 算例及参数影响分析

3.1 疏散系统的物理环境

以下以一桥梁观光通道为例，进行火灾环境下行人疏散的模拟.系统的平面是以元胞为单位的平面坐标系，通道的网格尺寸为100×20(对应实际区域为40 m×8 m)，在通道的中部有20×10的障碍物区段，疏散边界的厚度为1个元胞，因此在非障碍物区段通道的宽度为7.2 m，在障碍物区段疏散通道的宽度为3.6 m.

给定初始人群密度DI=0.3人·m-2，则在非障碍物元胞处行人的生成概率Po=DI·Δs2.疏散系统的物理环境和初始人群分布如图 7所示.火源点的坐标为(70,10)，火灾按照表 2定义的传播速度蔓延.

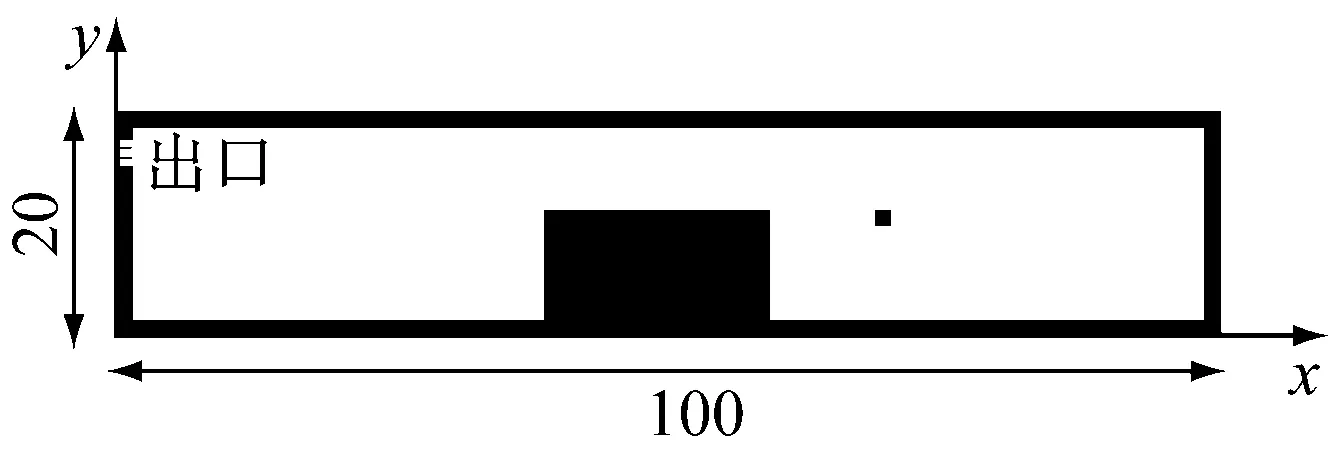
图7 疏散系统的物理环境

3.2 疏散模拟的基本参数和假定

示例模型的参数包括场强模型基本参数、行人的基本参数及火灾的蔓延规律.

场强模型的基本参数及其取值如表 1.行人的基本移动速度vb=2.5 m·s-1，视角αs=45°，视距rs=10元胞尺寸(对应实际4 m).

表1 场强模型的基本参数

火灾模型采用单火源的初始条件，火灾由发生点向四周传播范围Rf与传播频率Tf的函数关系f(Rf)如表 2所示，火灾传播极限Rm=20.

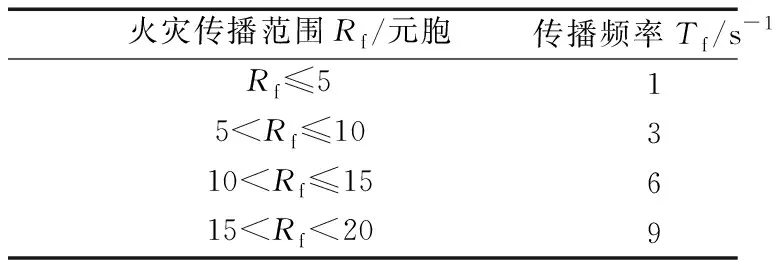
表2 火灾传播范围和传播频率的关系

3.3 疏散过程

疏散模拟过程中，t为当前模拟时间步长.图 8记录了行人在火灾蔓延环境下的疏散过程，记录时间步长集合为T={1,50,100,200,300,400}.

3.4 参数分析

疏散过程中行人的移动方向和期望速度的变化分别由镇静概率增长系数λ控制和期望速度折减系数下限γ.以下对λ和γ进行参数分析，讨论λ和γ对行人疏散过程、平均死亡人数和平均疏散过程的影响，并与不考虑期望速度调整规则和火灾下移动方向的基本模型进行比对.为减少随机误差的影响，各参数的模拟结果取30次重复计算的平均值.

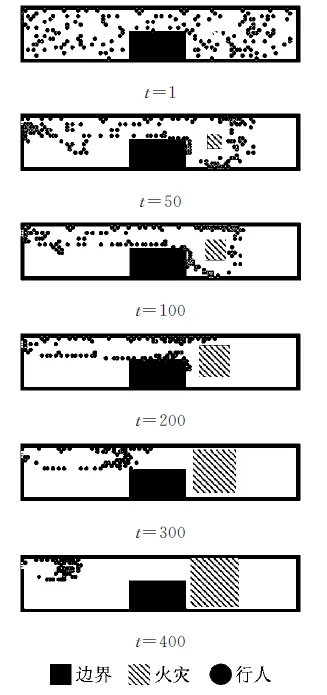
图8 火灾场景下工程结构内疏散过程

3.4.1基于火灾场景的移动方向

本组参数分析取λ={0.25,0.50,0.75}，并且不考虑期望速度调整规则的影响.系统内剩余人数(包括移动行人和死亡行人)随时间的变化如图 9所示.由图可见，当t<275时，成功疏散的行人主要初始分布于障碍物和出口间，这部分行人受到火灾的影响较小，即考虑火灾场景下移动方向的剩余行人变化曲线与基本模型并无二致.当t≥275时，成功疏散的行人主要初始分布于障碍物后方.这部分行人受到火灾的显著影响，呈现较为普遍的恐慌行为，以至于到达出口的时间较长.λ值越小，镇静概率增长速度越慢，行人更易于发生恐慌行为，火灾对疏散过程的影响也更为明显.因此，考虑火灾场景下的移动方向时，不同λ对应的曲线仅在时间步长t≥275后与基本模型出现偏离，λ值越小偏离程度越大.

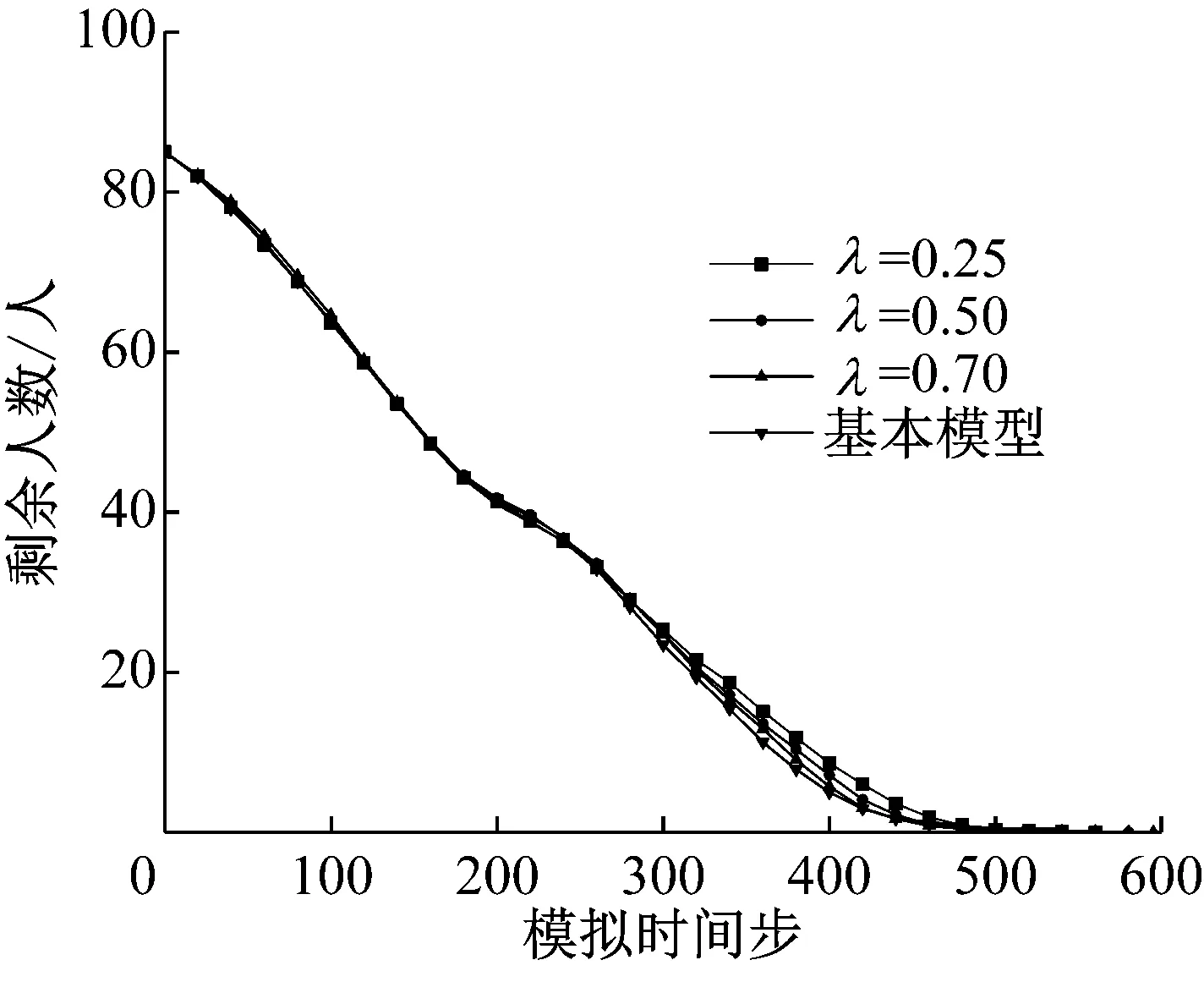
图9 不同λ值对应的剩余人数变化曲线

不同λ值对应的平均死亡人数和平均疏散时间如表 3所示.

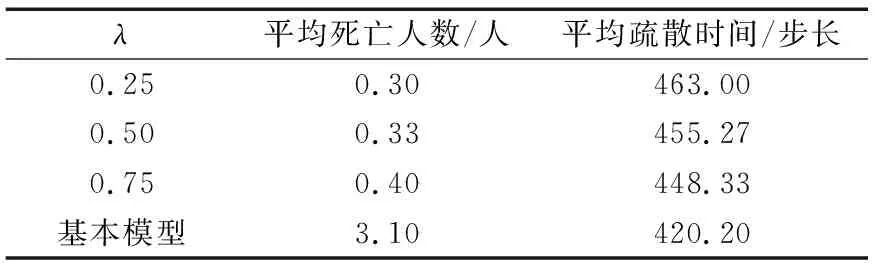
表3 不同λ值对应的平均死亡人数和平均疏散时间

考虑火灾场景下的移动方向后，行人的自我保护意识提高，平均死亡人数出现明显的下降，几乎可以保证所有人员的安全疏散.在模拟实例的物理环境中，考虑移动方向能够最大程度地规避火灾的潜在威胁，并且λ值越小，火灾对行人的心理作用越显著，行人会更倾向于采取远离火灾蔓延区域的行为.

行人主动远离火灾蔓延区域的代价在于偏离了前往出口的最短路径，行人整体的疏散时间相对基本模型明显增加，且平均疏散时间随λ的减小单调递增.

3.4.2基于行人流场景的期望速度

本组参数分析取γ={0.25,0.50,0.75}，并且不考虑火灾下移动方向的影响.系统内剩余人数(包括移动行人和死亡行人)随时间的变化如图 10所示.由图可见，当γ=0.50或0.75时，剩余人数随时间的变化曲线与基本模型几乎完全相同，而当γ=0.25时，曲线在时间步长t∈(250,400)的范围内与基本模型发生偏离.由此说明，当行人期望速度的折减并不显著时(γ≥0.50)，系统的疏散能力始终是饱和的；当γ进一步下降后，行人的整体移动速度降低，障碍物后方行人移动至出口的时间过长(如图8t=400时行人分布所示)，在这过程中系统的疏散能力并未得到完全发挥，以至于曲线出现偏离.

不同γ值对应的平均死亡人数和平均疏散时间如表 4所示.

拥堵导致火灾周边行人难以及时疏散，成为火灾环境下行人死亡的主要原因.采用期望速度调整规则后，行人会降低前往人群密集位置的期望速度，这在一定程度上减轻了拥堵水平，平均死亡人数较基本模型存在一定的降低.拥堵的水平主要取决于拥堵形成和消散的速度，降低γ值，同时降低了二者.当γ=0.75时，拥堵形成速度有所降低，尽管拥堵水平仍较高，此时行人具有较高的期望速度，保证了局部拥堵的较快消散；当γ=0.50时，拥堵形成速度进一步降低，拥堵形成的规模减小，但行人的期望速度明显下降，在模拟实例的物理环境中，将形成规模稍小但持续时间长的拥堵，导致平均死亡人数再次上升，但仍低于基本模型；当γ=0.25时，行人期望速度的调整进一步降低了拥堵的规模，行人移动速度虽慢但疏散过程顺畅，减小了火灾对行人的威胁，平均死亡人数降至最低.

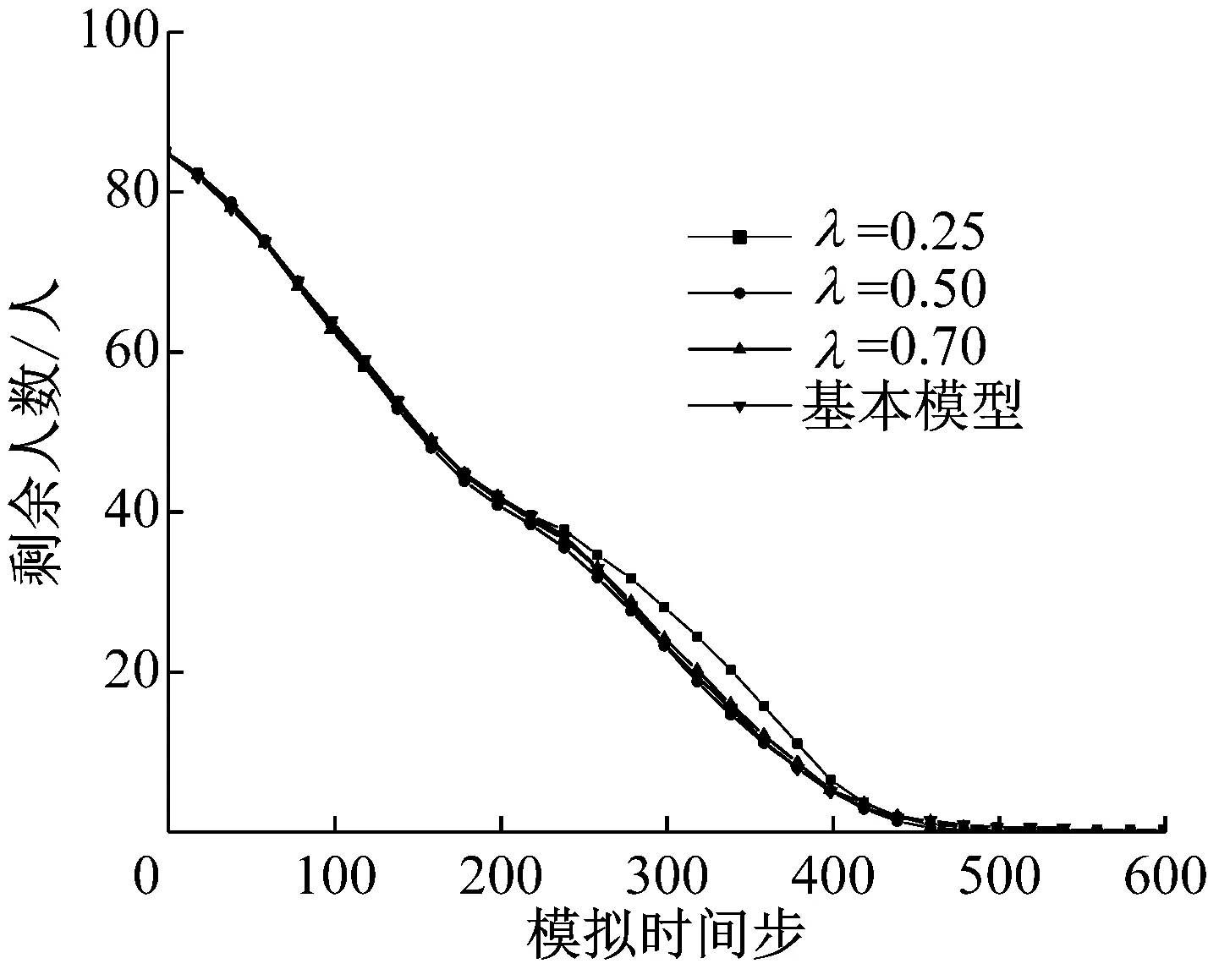
图10 不同γ值对应的剩余人数变化曲线

表4 不同γ值对应的平均死亡人数和平均疏散时间

采用期望速度调整规则后，平均疏散时间较基本模型有所增加，但增幅有限，说明当γ≥0.50时，系统的疏散能力均已达到饱和，采用更高的行人速度也无法减小系统疏散时间.当γ=0.25时，行人期望速度显著差异化，部分行人期望速度进一步降低，使行人整体疏散速度低于系统疏散能力，平均疏散时间增加.平均疏散时间的变化规律与图 10的剩余人数变化规律一致.

基于上述分析，在实际的疏散环境中，应当在易于发生拥堵的通道变宽处的入口设置醒目的标识，以减小行人前往通道的速度，避免出现过大规模的拥堵；在通道变宽处的出口应设置明显的方向指示或安排人员组织疏散，提高出口的行人速度，加快拥堵的消散.

4 结论

基于目前研究对火灾场景下人群疏散模拟方法的讨论，在场强理论的基础上进行了行人移动方向和速度调整的拓展研究.提出了基于火灾场景的移动方向规则和基于行人流场景的期望速度规则，并引入移动判定准则以描述行人的速度差异，进行异步行人流的模拟.最后，基于拓展模型对一桥梁观光通道进行了人群疏散仿真模拟，并根据模拟结果讨论了引入规则的影响.得到结论如下：

(1) 考虑基于场景的移动方向和期望速度规则后，疏散的总时间和平均死亡人数呈现一定的改变；

(2) 根据期望速度调整规则得到的行人速度并不是影响系统疏散过程的唯一因素，通道出口的疏散能力控制了系统疏散速度的上限；

(3) 期望速度调整规则影响了拥堵的形成规模和持续时间，进而影响火灾环境下行人的安全疏散，考虑期望速度后平均死亡行人数下降13.9%；

(4) 应当在通道变宽处设置标识或组织疏散，调整出入口的行人速度，减小拥堵的形成规模并加快拥堵的消散，以保障行人的疏散安全；

(5) 火灾场景下的移动方向主要影响了火灾附近行人的移动规律，显著降低了单火源下通道疏散的平均死亡人数(几乎降至0)，随着火灾对行人心理作用的增强，系统的平均疏散时间有所增加.

模拟单火源下工程结构的人群疏散时，仅考虑火灾场强的影响对行人安全的评估偏于保守.考虑行人期望速度的变化能有效地描述拥堵形成和消散的内在规律；火灾场景下的移动方向能够更为准确地反映行人在火灾环境中的应激行为.

在引入火灾场景下移动方向后，平均死亡人数下降明显，但疏散总时间明显增加.考虑到以上仅模拟了单火源的疏散过程，疏散时间的增加对行人的安全影响并不显著.因此，研究在多火源分布的工程结构疏散模拟中移动方向的具体影响，是后续工作的重点.