基于改进GM(1,1)模型的高校仪器设备维护费用预测研究

梁小华

(陕西理工大学 财务处， 陕西 汉中 723000)

高校仪器设备是人才培养、教学、科研以及创新创业教育的基础性物质条件，在国家政策引领下高校仪器设备投入增幅明显(不乏百万级、千万级仪器设备)，加强高校仪器设备类国有资产管理不容忽视[1-3]。仪器设备良好的维护对提高实验水平与效率、避免实验事故和延长使用寿命以及发挥国有资产价值都有重要意义。合理的维护经费预算是高校仪器设备科学维护的前提[4]，因此对高校仪器设备维护费用进行预测是有必要的。而目前高校具体设备维护数据非常难找且数据少，基于这种现状本文采用灰色预测方法来进行研究。灰色系统理论相比回归分析预测法，在未来趋势预测方面具有对原数据要求低(样本数≥4)、计算精度高且易于操作等优点[5-6]。本文以灰色GM(1,1)模型[7]为基础，通过背景值和初始条件改变建立基于改进灰色GM(1,1)模型的仪器设备维护费用预测方法，案例应用实现了某加工设备“十三五”五年期的维护费用预测。

1 GM(1，1)模型及改进

1.1 GM(1，1)模型及建模过程

(1) 设原始样本数列记为X(0)，

X(0)={x(0)(i)|i=1,2,…,n};

(1)

(2) 对X(0)做一次累加生成得到生成递增的新数列X(1)，记：

(2)

(3) 求X(1)的邻近均值生成数列Z(1),记为

Z(1)={z(1)(k)|k=2,3,…,n}={[x(1)(k)+x(1)(k-1)]/2 |k=2,3,…,n} ;

(3)

(4) 对X(1)建立白化方程，其中a为模型的发展系数，b为灰色作用量，记为

(4)

(5) 灰色微分方程为x(0)(k)+az(1)(k)=b；

(5)

(7) 对灰色微分方程求解，确定a，b值，得到X(1)的灰色预测模型为

其中k=1,2,…,n;

(6)

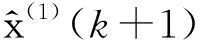
其中k=1,2,…,n;

(7)

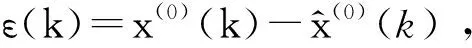
(8)

1.2 GM(1，1)模型改进过程

文献[8]和文献[9]表明原数列、灰色背景值是影响灰色GM(1,1)模型预测精度和适用性的关键因素。鉴于此，本文以常规灰色GM(1,1)模型为基础对上述方面进行优化改进。

(9)

后续过程依次类推。

(10)

其中，k=2,3,…,n。

(3) 模型改进后的精度评价。改进GM(1，1)模型的预测精度决定其结果的有效程度，改进后精度采用后验误差检验方法检验，利用公式(9)获得均值E与方差，对应的均方差比值Q和小误差概率P：

(11)

依据灰色GM(1，1)模型精度标准以及均方差比值Q、小误差概率P方可判定预测的精度水平。表1为预测精度等级标准。

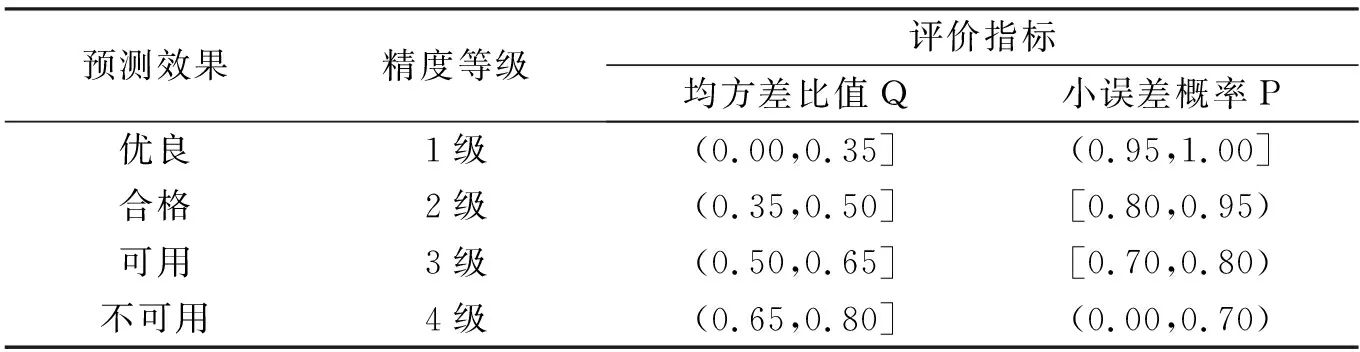
表1 预测精度等级标准

2 高校仪器设备维护费用预测

2.1 预测过程建模

问题描述：本文以高校某型号5轴铣削加工中心(原价368万元)为对象，已知该设备在“十二五”期间的实际维护费用情况下(见表2)，利用改进灰色GM(1,1)模型对“十三五”期间(2016—2020年)的维护费用进行预测研究。

表2 “十二五”期间该设备的实际维护费用

(1)建立常规灰色GM(1,1)预测模型。设定表2中的维护费用为原始序列，记为X(0)={3000，3816，4625，4850，5190}，利用MATLAB程序和公式(1)—(7)计算获得常规灰色GM(1,1)预测模型参数，a=-0.092 067、b=3 543.3，其数学表达

(12)

(13)

2.2 模型可能性分析

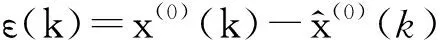
表3 两种模型预测对比

可见，改进模型的最大相对误差为1.94%，常规模型的最大相对误差为5.15%。与常规GM(1，1)模型相比，改进灰色GM(1，1)模型的残差绝对值和相对误差均优化效果显著，改进模型能克服数据扰动导致误差增大的问题，有利于小样本数据中长期预测。

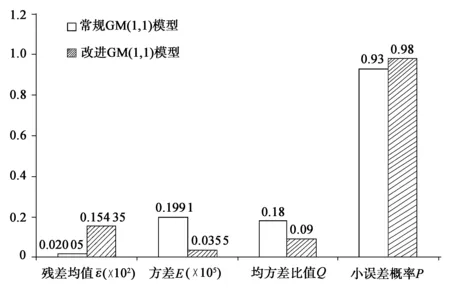
图1 改进前后预测模型的四项指标对比

综上所述，改进GM(1，1)模型的预测结果可信度较高，预测的高校某型号5轴铣削加工中心维护费用准确，符合仪器设备管理资产管理要求。

2.3 后五年结果预测

通过所建立改进GM(1，1)模型的数学表达式公式(13)可以对该设备2016—2020年五年期维护费用进行预测，见表4。可见，到2020年高校某型号5轴铣削加工中心维护费用达到7 714.2元，是2015年的1.48倍。

表4 高校某型号5轴铣削加工设备的维护费用

3 结束语

本文针对高校仪器设备维护经费预测方法的研究。分析了常规灰色GM(1,1)模型对小样本数据未来趋势预测的基本过程，基于此对影响预测精度的背景值和初始条件进行改进，建立了面向高校仪器设备维护费用预算决策的改进灰色GM(1,1)模型；通过改进前后两种模型的多指标比较分析，确定了改进模型的可行性和精度水平。以高校某型号5轴铣削加工中心为案例进行了未来五年期维护费用预测。实践证明，基于改进GM(1,1)模型的高校仪器设备维护费用预测，符合预测精度要求且准确地反映了实际情况，该方法为设备类国有资产维护经费预算决策提供了理论支撑。