归纳高中数学三角函数高效的解题技巧

胡青松

（榆树市第一高级中学校，吉林 长春）

一、分析高中数学三角函数问题特征

在平面、立体几何以及函数问题的解答中，多数情况均需拥有三角函数，尽管纯三角函数问题占据比重不高。所以，数学教师需促使学生在课堂教学中掌握有关三角函数的知识理论，让学生保持较好的学习成绩。三角函数在高考中，一般作为解答题的第一题，不具备较大的难度性，学生可通过多种方式进行解答，因这些问题相对较为灵活，所以对于问题的解决，教师可选择最简单快捷的方法进行；三角函数这一章节中有许多需学生记忆的公式数量，所以数学教师需要针对公式的原理，在开展这一章节的教学中进行分析，从而将学生对三角函数公式的记忆有效增强；在其他理科学科中，有关三角函数章节的知识均会被应用，所以教师需联系起和三角函数有关的科目知识，在教学的过程中促使学生将三角函数问题的相关解题技巧真正掌握。

二、高中数学三角函数高效解题技巧的归纳总结

1.强化审题的重要性

一些实用的技巧及方法在解答三角函数问题中需特别注意：针对较熟悉的题目，不可盲目地模仿，需和之前做过的题目进行异同的对比分析；要做到“咬文嚼字”，认真读题。不可不求甚解便开始盲目做题；要克服粗心的毛病，养成细心审题的习惯，特别是需提升解题的准确性，注意挖掘题目中隐含的条件，避免“会而不对”情况的出现，提升解题的准确性；当遇到新的题目时，需搞清楚未知及已知间的联系，分清条件及结论，找准解题的切入点。

2.加强练习，丰富解题思路

在高中数学中想要提高过学习及解题技巧的能力，其实并无简单化的途径，多多练习总归是一条明智的途径选择。所以，为了丰富学生的解题思路，需结合起理论知识及实际的练习，如在学习三角函数正弦定理的过程中，为了提升学习的质量，需要加强此习题的练习。如：A、B、C是锐角三角形的各个内角，则a、b、c是相对应的对边，已知a=2bsinA，求B的大小。在解答的时候，可按照sinA=2sinBsinA这一正弦定理，所以在已知a=2bsinA的基础上，得sinB=。此题无非是对学生学习正弦定理的掌握程度，只有不断加强三角函数强化练习，加强解题技巧，熟练地掌握基础知识，才可有效提升学生三角函数学习的能力。

3.升幂降幂

三角函数幂次方在多问题中是不同的，且数的幂次方和三角函数有关，学生在解答数学问题的时候无法对其公式直接使用。而采用升幂或降幂的方法，解答过程更简单。对于学生来说，升幂降幂解答技巧相对较为陌生，不太具有熟悉感，但是可取得非常显著的效果，在对不同幂次方三角函数的处理上。对sin2α+cos2α=l及其相关变化的灵活应用是升幂降幂解题技巧的关键。如对升幂降幂技巧对此题进行解答的关键，也就是说要使得幂次方达到一致，按照要求分别使用升幂和降幂处理。得出下述两个等式，通过分别进行降幂和升幂处理，经过推导得出

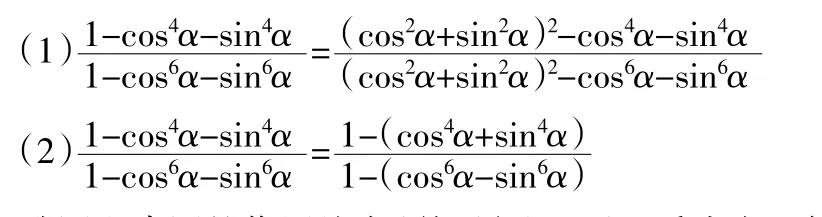
升幂和降幂的作用从本题解题过程可以看成在于简化原式，需从题干中挖掘出关键条件，以及发现问题隐藏。

4.平方法的使用

平方法在解析三角函数的过程中较为常见。教师可在答题的过程中，让学生分析存在的题干，假设涵盖余弦、正弦内容均可考虑应用平方法进行问题的解答。如：方程x2-kx+k+1=0中，sinθ、cosθ是其两个跟，已知θ∈（0，2π），则求出k的值是多少？教师需建议学生遇到此类题型的时候，需凭借韦达定理来计算出k的值。通过运算便可得出k的值会有2个，通常情况下因为不满足值域，其中一个值会被舍去。因此得出k=-1，舍去的是k=3这个根。而老师必须要指导学生注意，在回答这一种类型三角函数中，学生应先学会此种最基本方式，之后再选择取倒数、取平方方式。较为牢固的基础知识是开展三角函数知识教学中教师需对学生进行的指导。

5.解题技巧中的数学思维总结

弦切互化、巧设参数、升幂降幂主要包含以下几种解题思维。（1）函数和方程思想。可将函数思想用于解答方程，都可互相转化，也可把方程知识用于理解函数。基于二者的联系需同时考虑，把问题简化；（2）化归思想。多个不同转化成单一三角函数；多个不同角度的转化成单一角度三角函数；不同幂次转化成同幂次三角函数等等；（3）还元思想。之前的变量通过新的替换，促使解答过程更简化，新的变量更简单，达到对之前原有问题结构简化的效果。