基于Adaptive Lasso与RF的航班运行风险预测改进研究

2018-09-10王岩韬陈冠铭杨远浩

交通运输系统工程与信息 2018年4期

王岩韬，陈冠铭，刘毓，杨远浩，赵航

(中国民航大学国家空管运行安全技术重点实验室，天津300300)

0 引言

航班运行是一个连续动态过程，其影响因素种类、形式、数目繁多，运行风险随条件不断改变.面对此复杂系统，构建科学的评估和预测方法是提高安全水平的必要措施.欧美民航安全管理和风险定量研究在2000年后已有成果，但因国内和欧美运行环境相差巨大，导致模型无法移植使用[1-3].国内民航对航班运行安全的研究于2010年后起步，从孙瑞山教授开始至王岩韬等，已完成从研究方向、预期目标、解决方案等多方面完整探索[4-5].2015年下发的咨询通告《航空承运人运行控制风险管控系统实施指南》作为研究成果的典型应用，标志着中国民航已建立了通用性、示范性的航班风险评估体系.截止2018年初，国内52家运输航空公司以此前研究为基础开发了航班运行风险控制系统，使用核心算法包含模糊隶属函数、风险矩阵、支持向量机和概率论等[6].上述方法存在部分缺陷，例如过度依赖专家主观评价等已在文献[7-8]中详细论述.目前在一线应用中亟待解决问题还包括：第一，由于评估项目数量多、计算过于复杂，致使响应速度慢，无法满足使用需求；第二，在训练样本得到较高精度的基础上，测试和应用精度有时反而降低，即出现了过拟合现象.目前实践应用中日运行精度处于[0.782,0.875]之间，计算精度不高且稳定性不足[7-8].

基于上述情况，利用Adaptive Lasso擅长处理高维变量及RF有效处理过度拟合的特点[9]，建立Adaptive Lasso与RF的二阶段混合预测模型，使用某航450组航班运行数据，验证模型可用性.通过与PCA、RBF神经网络、SVM进行对比，验证方案有效性和可靠性，旨在为航班运行风险管控工作探索有效、快捷、准确、稳定的预测技术.

1 样本数据

1.1 数据选取

如文献[6]中详述，某航将运行总风险分为机组方面、飞机方面、进近着陆阶段威胁3大类共63项影响因素.精选该航2017年风控系统历史数据共450组，包含风险高、中、低3级各150组；由飞行、签派、机务等专家逐一检验，发现其中18组存在偏差，经专家组商议并修正结果后，该450组航班数据作为标准样本集合，如表1所示.

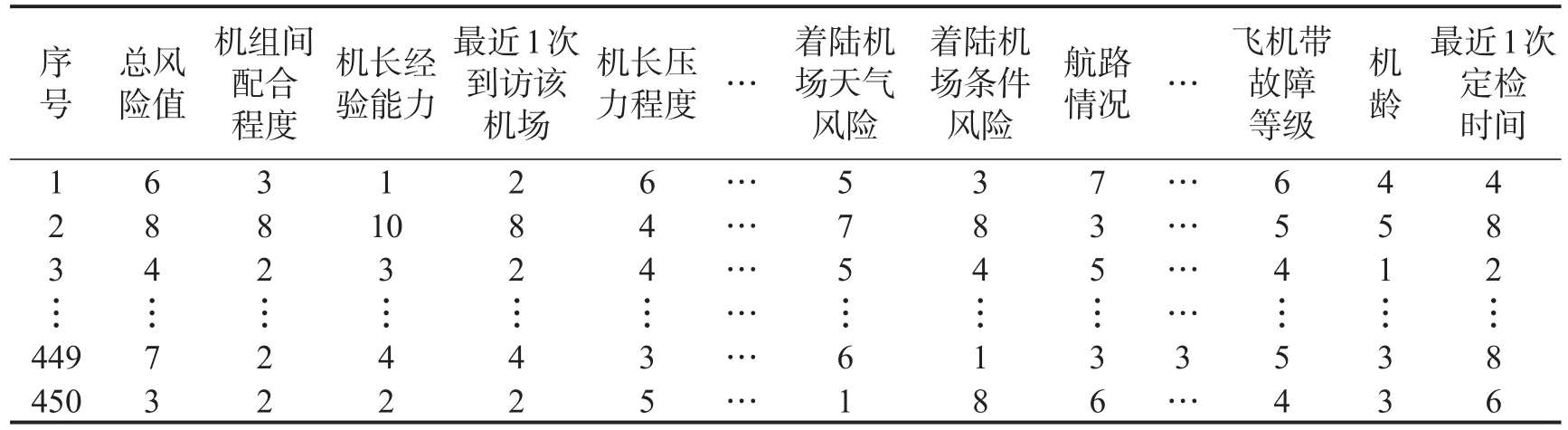
表1 航班运行风险数据集合Table 1 Flight operations risk standard data set

1.2 应用分析

在实践应用中，各因素需在数据接入层提取，先做单因素评判，再递进向上计算总风险，具体如图1所示.根据某航信息和运控部门实测，平均航班运算结果更新耗时3.6 s，响应速度不能满足运行人员使用需求；此外，现有系统预测结果稳定性不足，部分时段其计算精度低于80%，而在亟需查找原因纠正错误时，评判因素越多，难度越大[5].综上，下节采用Adaptive lasso算法进行降维，以求精减评估指标项.

2 指标降维

2.1 算法简介

Adaptive Lasso是一种高维数据线性回归方法，本质是改进的两步法Lasso[10].定义β=(β1,β2,…,βm)T是回归系数；Aj=(a1j,a2j,…,anj)T是预测变量，其中j=1,2,…,m；Y=(y1,y2,…,yn)T是响应变量.对所有的非负的常规参数λn，求解Adaptive Lasso问题公式为，其中，；为普通最小二乘法所得系数估计值.

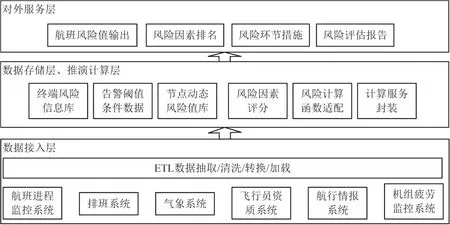
图1 风险管控系统业务和数据架构Fig.1 Risk control system dynamic business and data architecture

2.2 降维计算

此处，利用RGui软件对63个风险指标进行计算，得到性能价格比Cp值，如表2所示.Cp值用来衡量多重共线性，其值越小越好.

表2 各指标Cp值Table 2Cpvalue of indicators

由表2可知，在R程序运算过程中，Cp最小值为12.869，此时总风险有效影响因素共有15个，分别为机组配合程度X1、机长经验能力X2、副驾驶经验能力X3、机组疲劳程度X4、机组压力程度X5、机龄X6、MEL/CDL风险X7、起飞机场天气风险X8、起飞机场条件风险X9、着陆机场天气风险X10、着陆机场条件风险X11、航路风险X12、航路备降机场天气风险X13、航路备降机场条件风险X14和特殊运行种类(二放、极地、延程运行等)X15.

3 精度分析

以X1～X15为指标体系，使用支持向量机算法，取400组航班标准数据作为训练集，剩余50组作为测试集.使用Matlab中LibSVM函数，参数优选使用SVMcgForClass，最优惩罚因子e和核参数g通过交叉验证法确定，具体计算过程如文献[5]，得到样本训练分类正确率为85.6%，同时确定e=3.042 1，g=0.562 43.

更新模型参数为最优e和g后，如图2和图3所示，测试结果正确率仅为84%，与文献[5]中情况类似，训练优化后得到测试精度无实质提升.进一步分析发现，上述指标中存在部分交叉关系，例如X15是综合了X10～X14限制条件下制定所得的飞行方案，而X4与X5也可能存在相互转化现象.因此推断模型过度训练和学习了数据中噪音，产生了过拟合运算现象.下节采用RF方法防止过拟合，使用RF处理前后的计算结果进行验证分析.

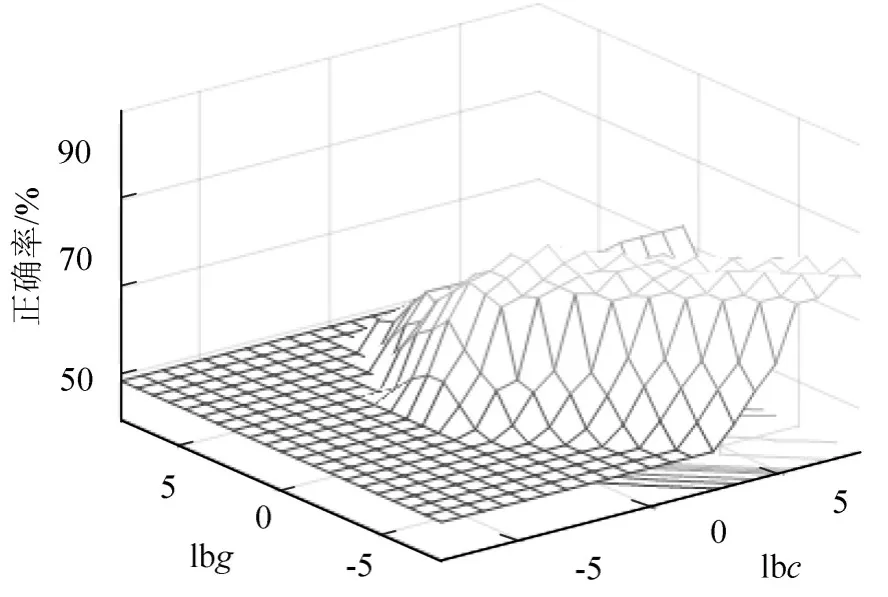
图2 参数优选结果(3D视图)Fig.2 Parameter optimization results(3D view)

4 防过拟合

4.1 变量重要性计算

RF可较好地处理异常值和噪声，对样本依赖小，能较好地解决多级分类问题，且不容易出现过拟合[11].

航班风险变量重要性的衡量标尺是各变量Xi导致结果的不纯度.不纯度计算公式为其中Q代表目标变量的类别总数，P(k/t)代表在节点t中第k类目标变量的条件概率.计算每棵树中以Xi为分裂变量节点的不纯度下降值，再将所有树的结果进行平均，从而得到Xi不纯度的平均下降值，下降越多则表示该变量越重要.通过SPSS Modeler评分系统对重要度进行打分，结果如表3所示.

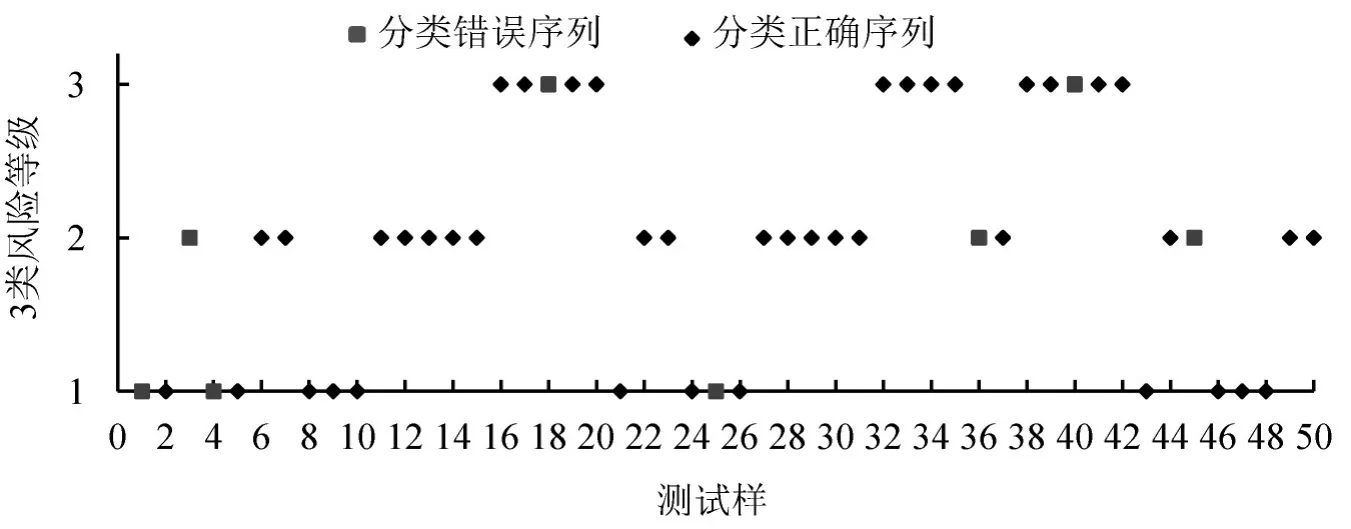
图3 风险等级分类图Fig.3 Parameter optimization results(3D view)

表3 指标重要度分值及排序Table 3 Index importance score and ranking

由表3分析可见，运行环境方面包括X8～X14，重要度总分值达到37.17，对总风险影响最大，其中着陆机场天气风险X11最为显著；飞行机组相关包括X1～X5，重要度分值达到 34.65，机长经验X2和机组疲劳X4影响最为明显.

4.2 误差计算

在处理航班运行风险模型过拟合问题时，在筛选变量过程中依次剔除表3中重要度分值最低的变量，再将剩余数据代入SPSS Modeler；同理计算14次后，可得到变量数为4～15的均方根误差和相对误差，如表4所示.可见当变量数为12时，预测结果的均方根误差和相对误差最小，稳定性最佳.故在Adaptive Lasso算法筛选结果后，再剔除航路备降机场天气风险X13、航路备降机场条件风险X14和特殊运行X15，保留有效变量12项.

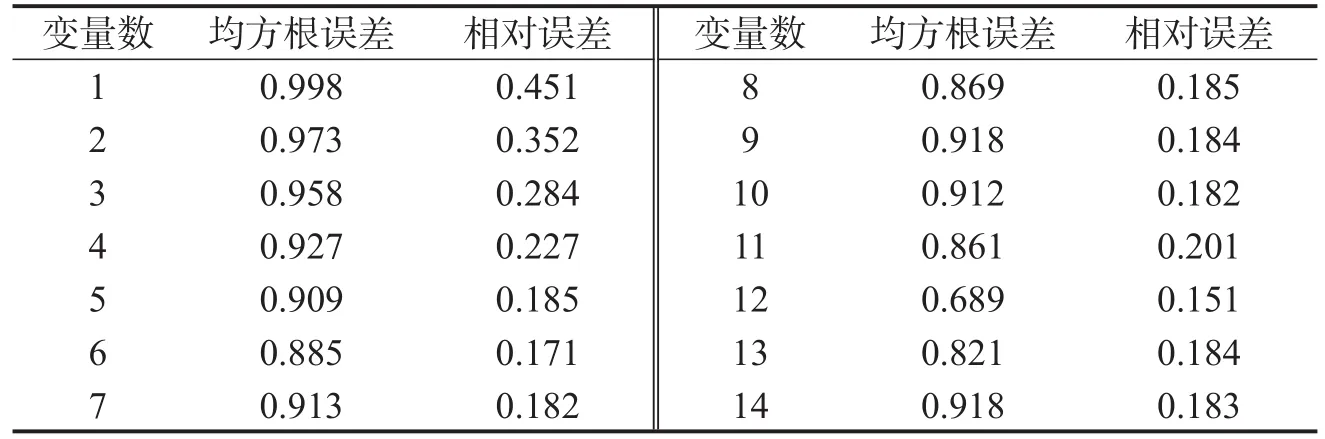
表4 各变量数的误差值Table 4 Error value of variable number

4.3 混合预测模型

RF作为一种机器学习方法，自身具有评估和预测计算能力.为达到降维和防止过拟合的双重目的，此处使用bootstrap抽样技术，从Adaptive Lasso筛选后样本抽取训练子集，对每一子集进行决策树建模，最后再组合所有决策树的预测结果.根据少数服从多数的原则，投票得出最终航班运行风险预测结论.

5 对比算法

5.1 PCA模型

在以往航班风险研究中，为了全面系统地分析问题，尽可能完整地搜集信息，每个观测对象往往包括多指标和变量，之间存在相关性，因此统计数据反映出的信息是有部分重叠的.PCA是将相关的指标转化成不相关的指标，避免信息重叠，达到利用较少新变量代替较多旧变量的降维目的[12].

主成分数学模型为

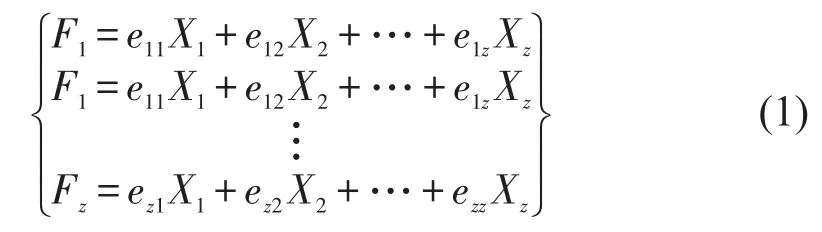
求得相关系数矩阵的特征值及主成分贡献率，如表5所示，以方差累计贡献率大于99%为主成分提取标准，选取前4个主成分.

表5 RF处理前后的主成分Table 5 Principal component before and after RF

RF防过拟合处理前，主成分1包含X1～X3、X7～X11、X13；主成分2 包含X3～X6、X8；主成分 3包含X10、X12、X15；主成分4包含X1、X13、X14.根据特征根及对应特征向量可计算得到主成分载荷，构建主成分与风险各因素的线性关系式如下.

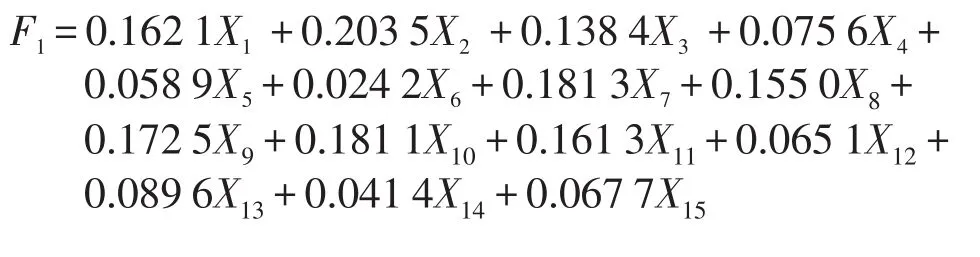
5.2 RBF模型

径向基函数(Radial Basis Function,RBF)神经网络由3层组成，包括输入层、隐含层和输出层.隐含层的神经元数目由具体问题而定，输入层节点只传递输入信号到隐含层，隐含层节点由高斯函数构成，输出层节点通常是简单的线性函数[13].

本处RBF使用newrb和newgrnn两种进行计算.newrb函数调用式为net=newrb(P,T,goal,spread,MN,DF)，其中P为输入向量，T为输出向量，goal为均方误差的目标，spread为径向基的扩展速度，MN为最大的神经元个数，DF是每次加进的网络参数.返回值是不断尝试得到的，创建网络后不断增加中间层数量和神经元数目，直到输出误差可接受为止.Newgrnn具有很强的非线性映射能力和学习速度，函数调用式为net=newrb(P,T,spread)，网络最后普遍收敛于样本量集聚较多的回归.

使用Matlab反复训练得到，在隐含层神经元个数等于7时，网络输出结果的均方误差仅为0.009 432 9，此时精度最高，即得到7-30-1结构的最优RBF网络模型.

6 结果分析

在 Adaptive Lasso 降维所得指标X1～X15基础上，根据表1标准航班数据集合，对RF处理前后两类情况分别使用混合算法、主成分分析、RBF两种方法、支持向量机进行仿真计算，将预测结果与实际值的相对误差进行对比，如表6、图4和图5所示.

为保证验证准确性和合理性，引入K折交叉验证(K-fold Cross Validation，K-CV)评估模型预测精度.K-CV可以有效地避免过学习及欠学习，此处使用十折交叉验证，即将初始采样分割成K=10个子样本，每个子样本都作为一次验证数据，其他9个样本用来训练.交叉验证重复10次，最终取平均结果得到估测值.

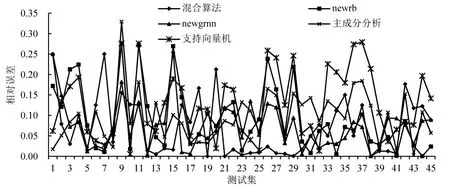
图4 RF处理前各种方法预测值相对误差Fig.4 Relative errors of various methods predicted values before RF

图5 RF处理后各种方法预测值相对误差Fig.5 Relative errors of various methods predicted values after RF

表6 RF处理前后各种方法结果汇总对比Table 6 Summary comparison of various methods predicted values after RF

由表6可知，使用Adaptive Lasso筛选掉48项指标后的平均精度高于90%，预测精度不降反升，说明Adaptive Lasso对航班风险预测问题可有效降维；经RF处理后，经RF处理后，5种方法所得精度有明显增长，均优于当前87.5%的日运行精度，尤其对于支持向量机方法，精度相比文献[5]有了大幅提升，说明随机森林方法可有效防止模型过度拟合，对处理航班风险预测问题有较强适应性；Adaptive Lasso-RF混合算法的预测精度可高达95.91%，优于主成分分析和RBF神经网络，也优于目前风控工作普遍使用的风险矩阵和支持向量机方法；同时，混合模型的CV值仅为1.45，是各类方法测得结果的最低值，说明其预测稳定性也为最优.