保障公益性运输服务的铁路客票管理策略
2018-09-10韩舒怡荣朝和
韩舒怡,荣朝和
(北京交通大学经济管理学院,北京100044)
0 引言
普速铁路的客运服务产品可以分为两类:公益性运输产品与普通运输产品.这两种运输产品的划分由服务的使用者决定,典型的公益性客运服务对象包括低收入人群、偏远地区人群、军用客运和抢险救灾人员调配等[1].在现行铁路客票管理中,并没有明确将这两种运输服务区分开来.理论上来说,公益性服务与普通服务的分开管理是可以实现的.主要原因有:①无论车站售票还是互联网售票,都可以通过检查或上传公益性保障运输享用凭证,实现精准的公益性服务受众划分;②目前铁路客票实行实名制购买与乘车,不存在“套利”可能.即公益性服务保障人群购买车票后,无法以高价将车票转售给普通服务人群使用.
厘清公益性与普通服务是铁路总公司作为市场主体,同时承担社会责任,进行市场化改革的必要步骤.铁路总公司作为市场企业经营主体,追求市场利益最大化是合理的经营目标.当然,作为国家企业或出于社会责任,也应该在一定范围内、通过合理的机制提供公益性服务.公益性运输服务的衡量指标不应该是利润,而是需求服务水平,即需求被预留车票满足的概率是多少.举例来说,如果某列车在A到B站之间的公益性需求均值为10人,标准差为3,而该列车在A-B区间预留的公益性运输客票有12张,则有12=10+z×3,其中z是公益需求的第z分位数,也就是公益需求的服务水平,即z=(12-10)/3=66.67%.铁路需要考虑如何设计合理的客票分配策略,在保障基本的公益性出行服务需求的同时,使铁路企业利润最大化.
目前国内外关注不同需求层次的铁路席位分配问题的人并不多,单杏花、包云、骆泳吉等人的研究主要关注铁路应该如何在沿途上下的区间段分配客票,即票额共用、席位复用的问题.航空客运业已有很多研究讨论如何在不同需求层次之间分配机票的问题[2-3],且关注到了运输产品低残值的特性,即航班一旦起飞,剩余席位的价值为0.也有学者[4]考虑了空间或预算约束下的航空客票分配问题.但是航空运输并不是一种普遍出行服务,这种特性决定了航空企业可以只追求利益最大化,无需考虑保障公益性需求服务水平,这与铁路客票管理的目标有很大不同.一般保护拥有优先权市场需求的办法有两种:一是规定该市场需求的最低服务水平,预分配一部分固定的席位给被保护市场,作为其专用的资产[5-7].还有一种体现在时间安排上[8-10],即先满足优先级高的需求,推迟满足优先级较低的需求.目前还没有研究关注空间能力约束下,低残值商品的双优先权保障问题.
1 现行混合策略与分离可调配策略
为了描述问题,符号定义如下:下标w和c分别代表公益性运输服务与普遍运输服务;下标数字1和2分别代表混合策略和分离可调配策略;下标字母a~b,d~h分别代表两个策略中总需求或不同市场需求的缺货、未售完与转运后状态.假设需求D服从正态分布,即D~N(μ,σ).其中,μ表示均值,即该时段内(例如:淡季)该趟车次的平均需求数量;σ表示方差,用以衡量实际需求偏离均值的离散程度.为了不同策略的可比性,我们假设两类市场需求在两种客票管理中保持一致.车票价格为p,单位供给成本为C,g表示每单位的未被满足的需求的缺货损失成本.假设两类市场的价格、成本、缺货损失成本相同.
1.1 现行混合策略
混合策略考虑联合需求Dt,即Dt=Dw+Dc,且Dt~N(μt,σt).基于联合需求制定总库存决策,决策变量是总订货量Qt1.决策目标是最大化铁路企业的总利润,并满足客票能力约束.目标函数是铁路企业的总利润Πt1,包括两个部分:有剩余库存情况下的利润Πt1a与缺货情况下的利润Πt1b.总订货量应该小于能力上限M,即
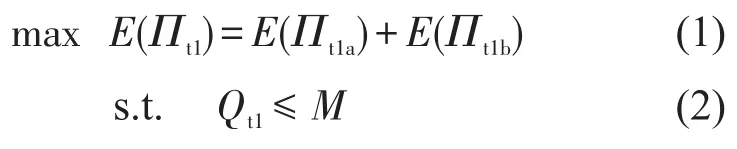
有席位剩余情况a下,即总需求Dt小于席位数量Qt1,企业的利润Πt1a包括收入与销售成本.收入等于价格p乘以联合需求Dt.销售成本等于单位成本C乘以订货量Qt1,即
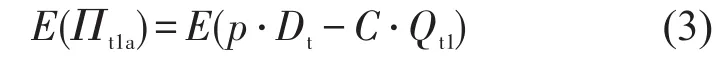
式中:E(∙)代表积分限内目标函数的期望.以式(3)为例,有

总需求Dt大于席位数量Qt1的情况b中,企业的利润Πt1b包括收入、销售成本与缺货损失成本.其中,收入等于价格乘以总订货量,成本等于单位成本乘以订货量,缺货损失等于单位缺货损失乘以缺货数量,即需求Dt减去Qt1为
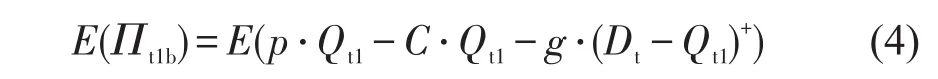
在能力约束式(2)下求解式(1),其中Q*t1u类似于经典报童问题的解[16-17],即
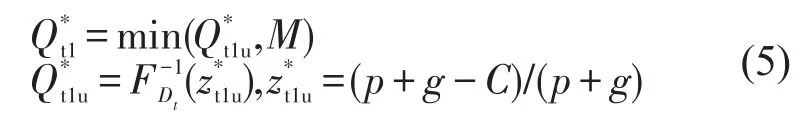
铁路现行的客票分配规则是各类需求先到先得,售完为止.类似于文献[3],公益性运输市场预期能够使用的车票数量Qw1可以写为kw⋅Qt1,其中kw=μw/(μw+μc).
1.2 分离可调配策略
分离策略考虑一个订货周期内的2个阶段.在预售期开始到开车前24 h,公益性服务与普通服务分别使用各自分配到的席位满足需求;在开车前24 h到开车时点,如果普通服务席位售完,而公益性服务车票还有剩余,则可将剩余的公益性车票在普通服务市场出售.
决策变量是公益性服务与普通服务的分配席位数量Qw2与Qc2.目标方程是最大化这两类市场的利润之和Πt2,包括5个部分,详见式(9)~式(13).2个市场分配到的席位数量之和应小于等于能力上限M,如式(7)所示;且公益性需求的服务水平应该大于预设的,如式(8)所示.

分别比较实际需求数量Dw,Dc和预分配库存数量Qw2,Qc2的大小,有以下5种情况.
情况d普通需求Dc小于普通席位分配数量Qc2,公益性需求Dw小于公益性席位数量Qw2.定义Qt2≡Qw2+Qc2.2个渠道的总预期利润包括3个部分:普通市场收入、公益性市场收入与总成本,即

情况eDc<Qc2,Dw≥Qw2,即公益性市场缺货,而普通市场有剩余席位.2个渠道的预期利润包括4个部分,分别是普通市场收入、公益性市场收入、总成本与公益性市场的缺货成本,具体为
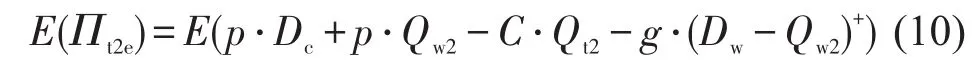
情况fDc≥Qc2,Dw≥Qw2,即公益性市场与普通市场需求数量都大于预分配席位.预期利润包括:普通市场收入、公益性市场收入、总成本、公益性市场与普通市场缺货成本,具体为
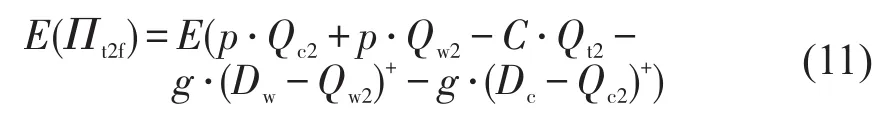
情况g和情况h在这两种情况下,公益性市场需求小于预分配库存,但普通市场需求大于普通市场预分配库存,即Dc≥Qc2,Dw<Qw2.比较普通市场的缺货需求数量(Dc-Qc2)和公益性市场剩余库存数量(Qw2-Dw),又分为两种情况:
情况g(Dc-Qc2)≥(Qw2-Dw).总利润包括:公益性市场收入、调配前普通市场收入、调配后普通市场收入、总成本与普通市场缺货成本.即
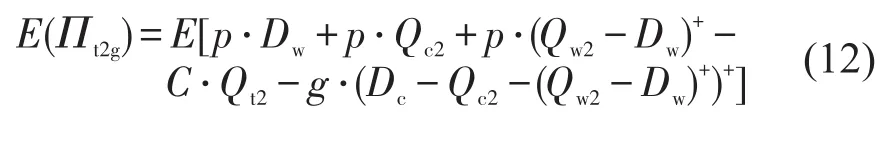
情况h(Dc-Qc2)<(Qw2-Dw).这种情况下的总利润包括:公益性市场收入、调配前普通市场收入、调配后普通市场收入与总成本.即

能力约束下的分离可调配策略求解:
在讨论约束解的情况前,先定义公益性市场的最少席位分配数量Qw2-low为
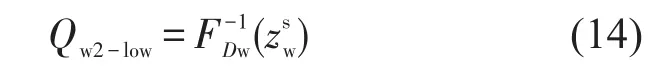
在约束式(7)和式(8)下求解式(6),解集如表1所示.

表1 分离可调配策略的解集Table 1 Cases and solutions for SDP policy
求解过程与Q*w2u,Q*c2u,Q*w2m,Q*c2m,z*w2u,z*w2m的定义见附录1.其中:
情况1无约束公益性需求服务水平z*w2u大于或等于预设值zsw,且无约束总席位供给量Q*w2u+Q*c2u小于或等于能力约束M,两个市场的席位分配量分别等于无约束问题的解Q*w2u和Q*c2u.
情况2当z*w2u<zsw时,公益性市场的席位分配等于最少席位分配数量Qw2d.如果服务水平约束下的总订货量Qw2d+Q*c2u小于等于M,则普通市场的席位供给量等于无约束解Q*c2u.
情况3当无约束总订货量大于能力约束时,席位总供给等于能力上限.其中,当能力约束的公益性市场服务水平z*w2m大于或等于zsw时,分离可调配策略的分配量等于能力约束解Q*w2m和
情况4当无约束总订货量大于能力约束,且时,公益性市场的席位分配等于最少席位分配数量Qw2d,普通市场的席位分配数量等于M-Qw2d.
管理启示为:
(1)当非约束或能力约束的最优公益性服务水平(z*w2u或z*w2m)大于预设的公益性需求服务水平zsw时,与经典报童问题相比(式(17)),企业会分配更多的席位给公益性运输市场,这与优先满足公益性需求的目标是一致的.策略具有良好的激励相容性,即管理者会自发的做出与系统期望目标一致的决策行为.
2 策略评估
本文分析了某铁路局特定车次3年的客运需求数据,结合实际运营情况.按需求总量多少分为淡季与旺季,按公益性需求占比高低分为低公益与高公益两种,形成4种典型案例:第1种是旺季—低公益,如旅游季;第2种是旺季—高公益,如寒暑运;第3种是淡季—低公益,如普通淡季;第4种是淡季—高公益,如应急救灾.
将旺季总需求均值设为1 900,淡季总需求均值为1 300.低公益与高公益分别指20%与80%的需求是公益性需求.假设两个市场的离散系数(Coefficient of Variant)相同,为0.13.则旺季—低公益中公益性需求的标准差为50,即0.13×380,普通需求的方差为200,即0.13×1 520,淡季为171.假设两类市场需求相互独立,旺季—低公益情况下的总需求方差为206.即(502+2002)1/2.其他3种情况同理,则4种情况对应的需求均值与标准差如表2所示.
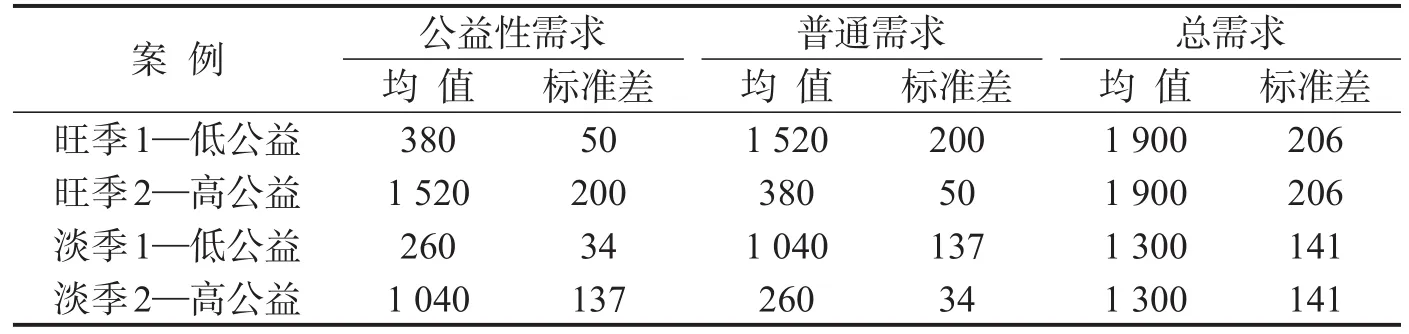
表2 4个案例的需求参数设定Table 2 Parameter values in public and common service demands (个)
模型的参数设定如下:价格p为580元,成本C为450元①0.缺货成本等于缺货系数乘以单位收益(p-C).我们设定缺货系数为10,因为作为基础性出行工具,铁路应该极力避免缺货情况.预设的公益性需求服务水平zsw≡80%.以标准19节车厢计,最大限员M≡2 000人.为了避免需求小于0的不合实际的情况,采用需求大于0的右截尾正态分布.仿真结果如表3所示.
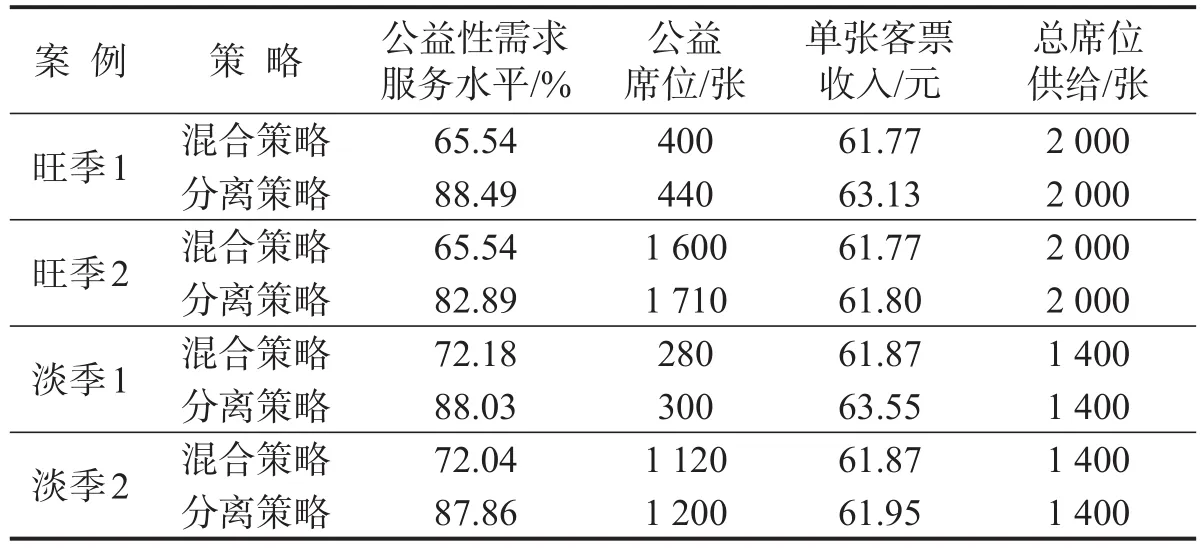
表3 两种策略的需求服务水平、单位利润与供给总量对比Table 3 Comparison of service-level,unit profit and supplier quantity
本文主要关注公益性需求的服务水平,定义两种策略的服务水平分别为z*w1≡Pr(Dw<Q*w1),保持各例中的总席位供给水平不变,对比混合策略与分离策略的公益性需求服务水平(表3,第3列),分离策略能够将公益性需求服务水平提高至少15.82%(淡季2,87.86%~72.04%).对比两种策略的公益性市场席位分配数量(表3,第4列),分离策略能使公益性市场席位提高至少6.9%(旺季 2,(1 710-1 600)/1 600×100%).对比两种策略的单张客票收入(表3,第5列),分离策略能够提高单张客票收入.注意,考虑到铁路运输产品通常以车厢为单位,而不是精确到座位(个),本文在十位数水平讨论席位供给量.
3 结论
区分普通铁路的公益性服务与盈利性服务是铁路运价市场化改革的必要步骤.公益性运输服务应该追求公平,评价指标是需求服务水平;普通服务应该追求盈利,评价指标是利润.本文考虑了列车能力约束与公益性需求服务水平的约束,探讨了一种分离可调配策略的效果,即预售期开始时给公益性需求与普通需求各分配一定的席位,在临近开车前(24 h),可以将未销售的公益性席位调配给普通需求市场销售.
主要结论有:
(1)与现行混合策略对比,分离可调配策略无论在淡旺季,都能够优先保证公益性需求;
(2)通过剩余客票的可调配措施,能够提高客票使用效率,提高单位客票预期盈利水平;
(3)既有的列车开行方案就能够实现公益性需求保证与单位利润提升的作用.
该策略可以为铁路下一步普速列车客运价格市场化改革提供决策支持.
附录 分离策略下的最优值求解
不考虑能力约束与服务水平约束,由式(6)对Qw2与Qc2求偏导,可以得到非约束情况下的最优订货量.F(∙)与f(∙)分别是对应需求的累积概率密度与概率密度函数:

定义满足式(15)和式(16)的最优解为无约束情况下的最优解Q*w2u,Q*c2u,无约束解对应的服务水平分别为z*w2u≡Pr(Dw<Q*w2u)和z*c2u≡Pr(Dc<Q*c2u).对比经典报童模型的非约束解(类似于式(5)),即
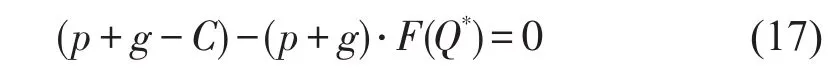
有Q*w2u大于经典报童问题解值小于经典报童问题解值


