求解双目标带时间窗车辆路径问题的蚁群算法

柴 获，何瑞春，苏江省，宋宇博，代存杰，马昌喜

(兰州交通大学a.机电技术研究所；b.交通运输学院，兰州730070)

0 引言

车辆路径问题(VRP)中存在这样一类问题，其配送网络是1个多重图，网络中边具有1个以上属性，使得任意两个节点间存在1条以上非支配路径，而一般车辆路径问题[1-3]是基于简单图.这类问题被称为多重图中的车辆路径问题(VRP on Mutilgraph,VRP-MG)[4]，通常其优化目标与边的属性一一对应，为多目标优化问题.例如，危险品配送VRP问题中，任意路段具有运输成本与运输风险两个属性，往往成本和风险是此消彼长的关系，问题的解为1组Pareto最优路径.

VRP-MG中任意两个客户节点间存在1条以上非支配路径，在安排车辆配送时，除节点间的配送次序会影响问题结果外，相同次序节点间不同路径的选择也对结果产生影响，因此，常见的MOVRP问题求解方法并不适用于此类问题.针对VRP-MG问题，部分学者设计了精确算法进行问题求解，Baldacci等[4]先进行拉格朗日松弛后，再采用列生成算法；Garaix等[5]设计了动态规划方法；Ticha等[6]设计了分枝定价算法求解带时间窗的VRP-MG问题(VRPTW-MG)，但精确算法对于具有一定规模的问题则不再有效.因此，启发式算法和进化算法是一个不错的选择，David等[7]设计了禁忌搜索算法；Pradhananga等[8]先采用标号算法确定两节点间的Pareto路径集，然后设计了蚁群算法对该问题求解，该方法中采用局部搜索与全局搜索相结合的方式，具有较好的收敛性，然而算法中并没有针对不同目标建立相应的搜索空间，在解的群体分布性和多样性方面存在不足.

本文以多重图中路段具有2个属性的带时间窗的车辆问题(Bi-objective VRPTW-MG,BOVRPTW-MG)为对象，建立了双目标优化数学模型，并提出用于求解双目标车辆路径问题的改进蚁群算法.

1 BOVRPTW-MG问题数学模型

在运输网络G=(N,E)中，N为n个节点的集合，包含配送中心0和客户节点集合C，E为节点间路段的集合.任意路段具有2个属性，因此，任意节点i,j间存在1条以上非支配路径.路径采用三元组(i,j,p)来表示，其中，p为节点i,j间的1条非支配路径；c(i1jp),c(i2jp)分别为路径p的2个属性；节点i,j间所有非支配路径集合为Pij.对于任意客户节点i(i∈C)，qi为节点i的需求量；[bi,ei]为节点i的需求时间窗；si为节点i的服务时长；[b0,e0]为车辆从配送中心出发和最晚返回配送中心的时间窗.K表示运输车辆集合，对于任意车辆k(k∈K)，CAPk表示其装载容量.xijpk表示车辆k是否经由路径p从节点i移动到节点j，如果是，xijpk=1，否则，xijpk=0.

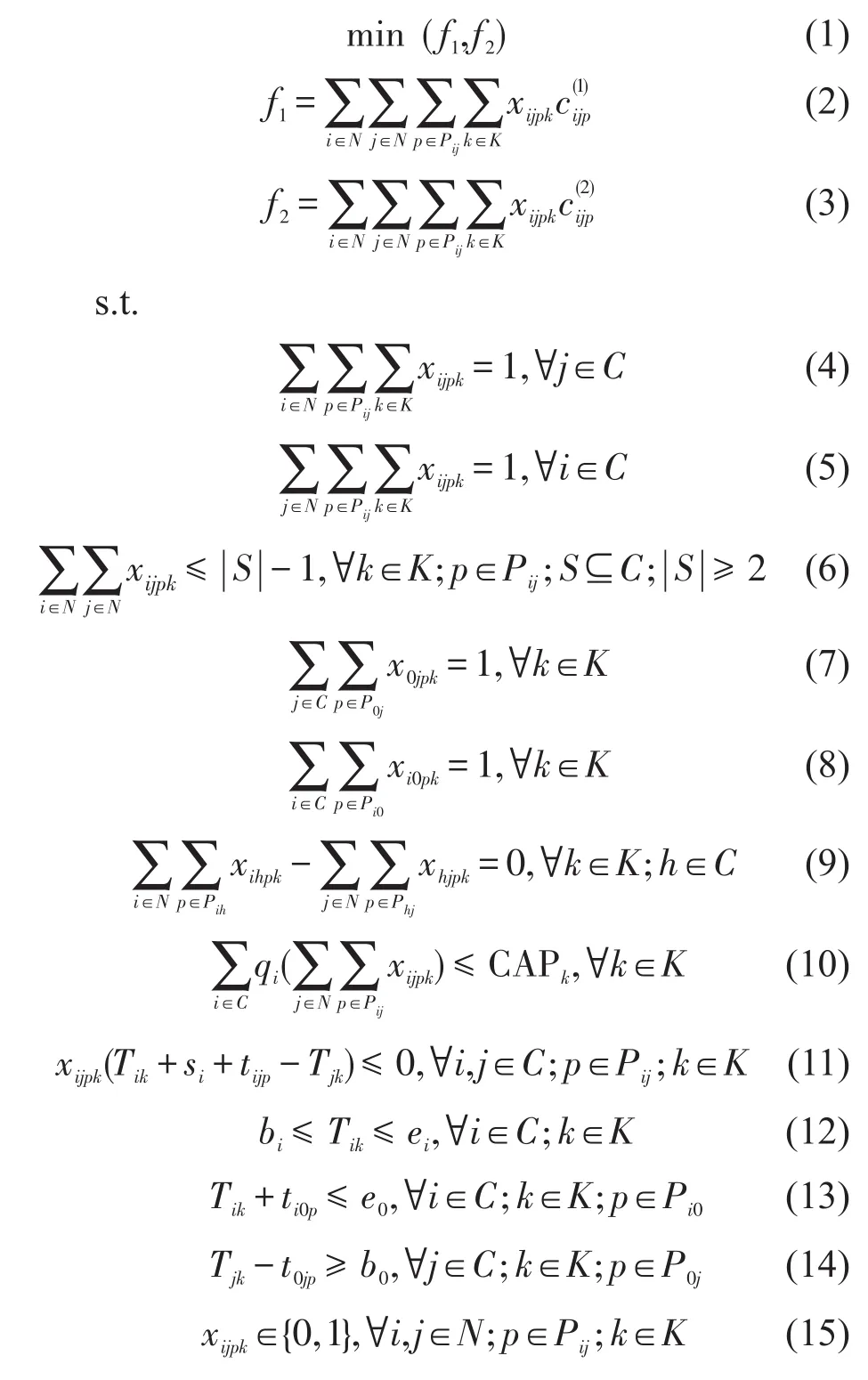
式中：tijp为车辆从节点i经由路径p到达节点j的运输时间；Tik为车辆k开始为节点i服务的时刻，如果车辆从节点i经由路径p到达节点j，则Tjk=max(Tik+si+tijk,bj)，即车辆k如果早于节点j的最早开始时间，则需要等待到时刻bj后才能开始服务.

式(2)和式(3)为目标函数；式(4)和式(5)表示任意1个节点由1辆车经由1条路径来服务；式(6)为子回路消去约束；式(7)～式(9)表示1辆车从配送中心出发，满足式(10)容量约束的条件下，服务完所有节点后再返回配送中心；式(11)表示车辆k在从开始为节点i服务至移动到下一节点j并开始服务过程中需要满足的时间条件；式(12)～式(14)为时间窗约束，式(12)表示车辆k到达节点i开始服务的时刻需要满足节点i的时间窗要求，式(13)和式(14)分别表示车辆k从配送中心出发和返回配送中心的时刻需满足配送中心的时间窗.

2 求解BOVRPTW-MG问题的改进蚁群算法

2.1 搜索空间

在多目标优化问题中，获得各目标最优的搜索方向不统一，而传统蚁群算法中蚂蚁只能朝1个搜索方向进行搜索，即获得单目标最优解.为了使蚂蚁能够朝着不同的搜索方向进行搜索，通过采用目标函数加权处理，即对于具有n个目标的多目标优化函数向量F=(f1,f2,…,fn)T进行加权综合为单目标优化函数F*=FTW，其中：W=(w1,w2,…,wn)，一旦向量W确定下来，蚂蚁的搜索方向也就确定，通过产生不同的权重向量W，经过多次求解可获得不同方向上的最优解，形成Pareto解集[9].

BOVRPTW-MG为双目标问题，需要在求解中不断更新权重向量.设定区间[0,M]，M∈N+，表示目标函数1的权重因子m(m=1,2,…,M)的变化范围，蚂蚁在经过某条路径时产生的信息素均与当前蚂蚁行进时的m取值相关，即在不同的m值下，蚂蚁的搜索方向不同，其产生的信息素及状态转移规则不同.关于M取值对解的分布的影响，在算例分析中进行讨论.

2.2 信息素更新

蚂蚁在释放信息素的同时，各路段上的信息素随时间推移也逐渐挥发，设参数ρ，0＜ρ＜1，表示信息素挥发系数，ρ越大，信息素挥发越快.当所有蚂蚁完成1次搜索，权重因子为m时各个路段的信息素按照式(16)实时更新.

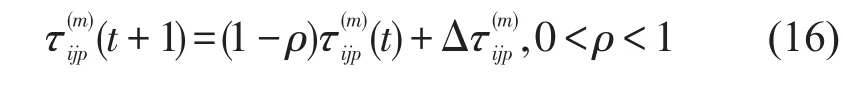
式中：τ(m)ijp(t)为t时刻后路段(i,j,p)上信息素浓度；Δτ(m)ijp为所有蚂蚁在经过路段(i,j,p)释放的信息素之和；，其中可根据Dorigo的蚁密系统模型[10]计算，即

式中：Q为常量，表示信息素质量.

2.3 状态转移概率

搜索空间m决定了当前蚂蚁的搜索方向，不同m值下同一路段具有不同的转移概率，蚂蚁由节点i通过路径p向节点j移动的概率pr(k)ijp(m)为

式中：τ(imjp)为路径段(i,j,p)在权重因子为m时的信息素[10]；ηijp=1/max(1,(Tjk-Tik)(ej-Tik))[11]为车辆在路段(i,j,p)上行驶时间的启发值；ω(i1jp)=1/c(i1jp)为车辆在路段(i,j,p)上行驶的权值c(i1jp)启发值；ω(i2jp)=1/c(i2jp)为车辆在路段(i,j,p)上行驶的权值c(i2jp)的启发值；α为信息素重要程度因子；β为启发函数ηijp的重要程度因子；γ为启发函数ω(i1jp)和c(i2jp)的重要程度因子；μ1和μ2分别为启发函数ω(i1jp)和c(i2jp)的权重因子表示当前蚂蚁剩余装载容量；Callow(k)为当前蚂蚁未到达过的需求节点集合.

文献[8]将蚂蚁平均分布到整个搜索空间中，为每只蚂蚁指定了搜索方向，由于每只蚂蚁的搜索方向不同，先出发的蚂蚁行走时遗留的信息素对其他蚂蚁的引导作用有限，并且可能产生误导.因此，本文将问题的搜索空间划分M个，针对每个搜索空间建立了不同的状态转移规则，引导所有蚂蚁朝相同的方向进行，最大程度的发挥信息素的引导作用.

2.4 算法步骤

如图1所示，针对BOVRPTW-MG问题的蚁群算法主要有2层循环，第1层根据不同的m值构建搜索空间，第2层循环为蚂蚁根据状态转移规则进行路径规划，每只蚂蚁遍历完所有需求节点后根据支配关系更新Pareto解集，并更新当前搜索空间中信息素.因此，算法的时间复杂度为O(M∙A).

图1 求解BOVRPTW的蚁群算法流程图Fig.1 Flow-process diagram of algorithm for BORVRPTW

3 算例分析

以25个客户节点的双目标带时间窗车辆路径问题为例，设定每个需求节点的时间窗、需求量及服务时间信息，采用随机方法生成所有节点两两间所有路径(边)的权值，形成共计1 336条路径的车辆配送网络(多重图).采用本文所提蚁群算法，获得节点1出发完成节点2～26配送任务的车辆行驶路径的Pareto最优解.

3.1 参数敏感性分析

程序采用C#语言编写，由于蚂蚁行走过程中信息素更新及状态转移概率公式中各参数取值不同会对解的分布情况产生一定的影响，在程序中通过对参数α,β,γ,ρ,M及A的不同取值进行多次实验，分析参数对解的质量的影响.

(1)状态转移概率公式中参数α为信息素重要程度因子，在分别取值0.0,0.5,1.0,1.5，2.0的情况下，运行程序获得的各自的Pareto最优前沿如图2(a)所示，α从0.0到2.0的变化过程中，α=0.0时解的质量最差，同时群体分布性和多样性也相对α取其他值时较差，说明所设计算法中信息素在状态转移中发挥作用；同时由图2(a)可知，在β=1,γ=2,ρ=0.1的情况下，当α=1.5时，解的质量最好.

(2)由图2(b)可以看出，时间窗启发函数重要程度因子β=1时，相比β取其他值时更容易获得最优解.

(4)M值是在多目标问题中划分搜索空间而设置的参数，其目标为了引导蚂蚁行走方向，从图2(d)中可以看出，当M≥10时，不同M值对解的质量影响并不明显.然而M取值却对算法的时间复杂性有较大影响.从图1算法流程图中可以看出，算法的主要循环过程有M⋅A次，因此，M值每增加1，算法循环次数将增加A.

(5)蚂蚁的数量决定的解的质量，足够多的蚂蚁是获得高质量Pareto最优前沿的保证.从图2(e)可以看出，就本文算例而言，当蚂蚁数量A取2 000时，解的质量最佳.然而蚂蚁数量决定了程序的运行时间，在可接受的运行时间内，蚂蚁的数量越多，取得最优解的可能性越大.

(6)信息素挥发系数ρ确定了前蚂蚁行走轨迹对后蚂蚁的影响，其值越大，前蚂蚁释放信息素挥发越快，对后蚂蚁的影响越小，从图2(f)中可以看出，当ρ=0.3时，Pareto解较其他情况更优.

3.2 算法比较与分析

(1)与NSGA-II比较.

NSGA-II算法[12]是多目标优化常用的方法之一，具有普适性.为了验证算法的有效性，针对该问题，同时设计基于NSGA-II的多目标优化算法，从运行时间，收敛性和分布度3个方面对算法进行比较.

首先，针对该问题对基于NSGA-II的多目标优化算法进行简要介绍.

图2 参数敏感性分析Fig.2 Parametric sensitivity analysis

① 编码及解码方式.

个体编码采用两段式定长自然数编码.第1段为所有配送节点编号，车辆1从节点0出发，按照前半段的次序逐节点进行配送，当遇到车辆装载容量或时间窗条件不满足时，车辆1返回配送中心，车辆2再从配送中心出发，依次类推；第2段为节点间路径选择序号，解码时通过编码值与到达对应节点间路径数量获得实际选择路径.如编码[1 3 5 4 2 1 2 1 3 1]，假设根据约束，在前半段编码中，车辆1配送节点1，3，5，车辆2配送4，2，为了直观的描述后半段的解码过程，采用cij表示节点i,j间的非支配路径数量，则编码可解析成如图3所示配送过程，其中箭头上的数值表示节点间的路径选择.

图3 解码过程示意图Fig.3 Schematic diagram of decoding process

② 种群进化策略.

通过传统的交叉和变异操作产生新个体，即可完成代际进化.值得注意的是，在交叉过程中，两个体交叉后前半段可能会产生重复编码而使得对应的个体成为非法解，将未交叉编码段中的重复值采用交叉段中交叉前的编码值代替即可.

为了比较2种算法，分别进行以下参数设置：NSGA-II算法中种群规模为1 000，迭代次数为100(经过多次测试获得，在此基础上通过增加种群规模或迭代次数对解的质量改变不明显)；蚁群算法中参数取值为α=1.5，β=1，γ=2，ρ=0.3，M=10，A=2 000(通过参数敏感分析获得).程序均采用C#实现，在个人PC机(i5-3470 3.20GHz，4G)上分别运行2个程序，图4为单次运行2种算法获得的Pareto最优前沿比较结果，从直观上看，蚁群算法获得解的质量明显优于NSGA-II算法.

图4 NSGA-II算法与蚁群算法获得的Pareto最优前沿比较Fig.4 The compare of Pareto-front using ant colony optimization and NSGA-II algorithm

针对算例，对2个解集间的覆盖率(CS)[13]和个体空间分布度(SM)[14]进行比较.前者表示2个解集之间的覆盖率，在文献[13]中用来评价同一算法不同代间解集支配关系的比较；在本文用其比较最优解未知情况下不同算法获得集合的优势，定义如式(19)所示.后者表示解集中个体的分布度，用来衡量解的目标多样性，其定义如式(20)所示.与此同时对比两程序的运行时间(CT).

式中：P,P'为2个独立的Pareto解集；di、分别为解集P中非支配边界上2个连续变量的欧几里得距离和这些距离的平均值.

式(19)中，a＞a'表示解a支配a'；CS(P,P')越大，表明P中支配P'中任一个体的个体比例较大，解集P相对解集P'更接近于Pareto最优前沿；如果P中个体全部支配P'中个体，则CS(P,P')=1，CS(P',P)=0.式(20)表示解集P中相邻个体之间的距离与平均距离间差距，这种差距越大，说明解的分布度越高，即多样性越好；如果SM(P)=0，则说明解集中只有1个解，而并非Pareto解集.

分别运行根据2种算法所设计的程序10次，取每种指标的平均值.表1为2种算法中各指标的比较结果.结果显示，蚁群算法的3个指标均优于NSGA-II算法.

表1 蚁群算法与NSGA-II算法各指标的比较结果Table 1 The compare of indexes using ant colony optimization and NSGA-II algorithm

(2)与文献[8]算法比较.

文献[8]中，危险品运输模型中存在2个优化目标，即运输时间和运输风险.由于运输时间受时间窗约束，算法无法直接用于本文算例，根据文献[8]的算法思想，在状态转移规则中保留原时间窗启发函数，增加另一目标的启发函数，用于本文算例计算.2种算法参数设置如下：文献[8]中算法参数取值为蚂蚁数量20 000，其他参数设置为文献中建议值；本文蚁群算法参数取值为α=1.5，β=1，γ=2，ρ=0.3，M=10，A=2 000；2种算法中总蚂蚁数量相同.图5为采用2种算法获得和Pareto最优前沿.

图5 蚁群算法与文献[8]算法获得的Pareto最优前沿比较Fig.5 The compare of Pareto-front using ant colony optimization and algorithm in reference[8]

同样运行根据2种算法所设计的程序10次，取每种指标平均值.表2为2种算法各指标的比较结果.比较结果显示：根据2种算法设计的程序在蚂蚁数量相同情况下平均运行时间相差无几，而解的收敛性和分布度方面，本文算法优于文献[8]算法.

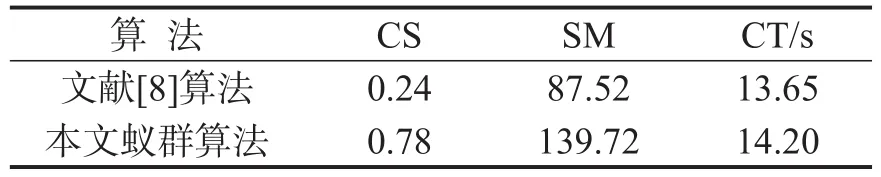
表2 蚁群算法与文献[8]算法各指标的比较结果Table 2 The compare of indexes using ant colony optimization and algorithm in reference[8]

4 结论

本文针对BOVRPTW-MG问题，在前人研究的基础上，建立了针对不同目标的解搜索空间，引导蚂蚁朝不同的方向进行搜索，提出了以搜索方向为参数的状态转移概率公式，设计了针对此问题的蚁群算法.

为了验证算法的有效性，同时设计了基于NSGAII的多目标优化算法，针对25节点间1 336路径的算例，分别采用NSGA-II算法，文献[8]算法和本文蚁群算法进行求解.通过比较可以看出，本文所提蚁群算法在运行时间、收敛性和分布度3个方面明显优于NSGA-II算法；相比文献[8]算法，相同蚂蚁数量设定下2种算法运行时间基本相同，而收敛性和分布度优于文献[8]算法.