考虑随机路网能力退化的连续双参考点用户均衡模型
2018-09-10魏庆琦
魏庆琦,肖 伟
(1.重庆交通大学经济与管理学院,重庆400074;2.电子科技大学经济与管理学院,成都610054)
0 引言
不确定背景下的出行择路和网络均衡是城市交通路网规划、政策设计和可靠性分析的基础.但是,出行个体的有限理性限制了基于传统期望效用理论的网络均衡模型的现实有效性,基于前景理论和累积前景理论的出行行为建模由此应运而生[1],成为近年来国内外交通行为建模仿真领域的热点.这些研究都将出行者视为有限理性的个体,并将最短路径期望到达时间视为参考点,当到达时间点位于参考点与工作开始时间之间时,出行者获得正效用.当到达时间点早于参考点或晚于工作开始时间时,出行者获得负效用[1-3].然而,出行行为研究者不断发现,用户并不将最短路径到达时间期望参考点作为正负效用的分界点[4].大部分研究认同,两个参考点就可以精确描述出行决策行为:一个是最优到达时间参考点,另一个是最早正效用到达时间参考点[4-5].当到达时间早于最早参考点或晚于工作开始时间时,效用为负;当到达时间位于最早参考点和工作开始时间之间时,效用为正;当到达时间越接近最优参考点时,用户获得的正效用越大[5].
这些文献主要是在累积前景理论和双参考点出行行为建模的基础上,对城市随机交通网络均衡、规划和管理进行了研究,但仍存在以下问题:①构造网络均衡模型时将交通网络的不确定性简单假设为出行时间正态分布,没有深入讨论路网能力退化造成的不确定性[6];②少量关于路网能力退化的网络均衡研究仅基于期望效用理论[7-8]或单参考点前景理论[3,9];③若干关于双参考点网络均衡的研究中,没有分析连续的随机路径时间,仅选择某几个值展开对比分析[6].针对这些问题,本文采用连续随机路网通行能力和连续路网能力退化下限,构造基于累积前景理论的双参考点用户均衡模型,证明模型解的存在性并设计了相应算法.在标定重要参数时,对连续路网退化能力下限和路段设计能力上限取值范围进行测试,以获取合理的参数值.模型将城市路网均衡的不确定性深入分析到客观天气、事故等导致的路网能力退化,以及主观的用户风险态度,可以更加精确地对不确定环境下城市交通网络均衡进行描述.
1 随机路网能力退化与连续双参考点
1.1 随机路网能力退化模型
路段时间基于BPR(Bureau of Public Roads)的路段时间模型为


1.2 基于连续随机风险偏好的参考点取值
路段随机退化导致路径时间也存在随机性,用户为保证达到时间的可靠性,在工作开始时间点之前设置1个最佳到达时间点T*,则风险控制预留时间.实际到达时间点ˉ时,产生迟到损失.T*<t≤Tˉ时,产生晚到收益.t≤T*时用户早到,存在1个可接受的最早时间点时,产生早到收益;时,实际到达时间距离Tˉ过早,产生早到损失.由此可将用户到达时间域划分为I、II、III和IV共4个区域:和,其中Td为出发时间点.
令

因此,有

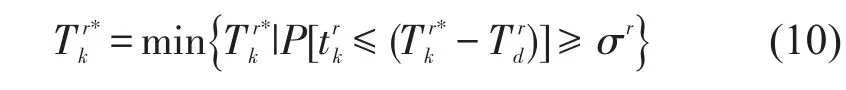
式中:Trd为OD对r的出发时间,因此有
式(11)表示路径时间长度在正态分布下累积概率密度函数的反函数.
1.3 连续双参考点累积到达时间感知价值
根据CPV交通行为理论,单一时间准则下,累积到达时间感知价值Vr,kATP最大化为择路规则[2-3].基于前文所述4个到达时区的划分,将用户累积感知时间价值Vr,kATP描述为
式中:i为到达时间区域类别,分别对应I、II、III、IV类;πi为时区i的决策权重;gi(t)为时区i的价值函数;-i和iˉ分别为4个时间区域的上界和下界.
当出行时间落在I和IV区时,用户价值函数取负,表示用户因为过早到达和迟到而不满;当出行时间落在II和III区时,用户价值函数取正,表示用户对出行时间满意,获得了正效用.对4个时区的价值函数进行定义,即

式中:Td为出发时间点;αi刻画时区价值函数的扁平程度,αi∈(0,1),可保证价值函数为正时为凹函数,价值函数为负时为凸函数;τi表示不同用户对获得或损失的偏好,τ4<τ1<0<τ2<τ3,表示在I、IV两区时间价值函数表现为损失,且等长度时间段的迟到损失大于早到损失.在II、III两区时间价值函数表现为收益,且针对最佳到达时间参考点而言,等长度时间段的晚到收益大于早到收益.同时,由于针对同一参考点,用户对损失的敏感程度大于收益,因此有-τ1>τ2,-τ4>τ3.
根据累积前景理论,当事件发生的客观实际概率为φ时,4个时区的主观感知概率分别为[6]

该函数保障了用户高估小概率的倾向.由此可获得到达时间tj落在区间i时的决策权重.
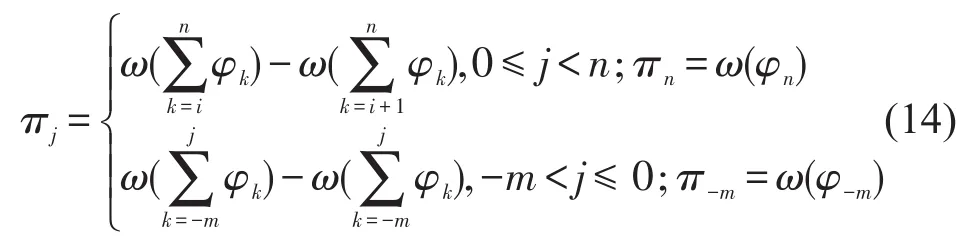
在到达时间连续随机分布时,令f(t)和F(t)分别为到达时间的概率密度函数和累积概率密度函数,得到

2 考虑随机路网能力退化的双参考点CPV用户均衡模型
2.1 均衡条件
类似于SUE模型,出行个体择路决策准则为路径累积感知时间价值VAr,TkP最大,路网流量均衡时,所有路径存在相等的,同时路径流量fkr>0;否则
2.2 均衡解存在性分析
可行路径集Γ为紧凸集,则存在任意f∈Γ,总存在唯一最近可行点p(f)∈Γ使f投影于Γ.定义1个映射,则当且仅当θ(f)=f时,有f是模型的1个均衡解[3,6].由于路径时间、路段退化系数及到达时间价值函数和感知概率权重函数均为连续函数,因此累积感知时间价值函数VATP(·)为连续函数,则θ(·)也连续,满足Brouwer不动点定理[3,6],VI均衡解存在.
3 求解算法
基于相继平均法(Method of Successive Averages,MSA)求解以上模型.
具体的算法步骤如下:
Step 1初始化.定义所有OD对可行路径集,基于初始路段条件,在所有路网零流状态下计算各路径累积到达时间价值.执行全无全有加载,获得初始路段流量x0a,置n=1.
Step 2计算路径累积时间价值.更新路径流量,获得新的路径累积时间价值Vr,kATP.
Step 3方向搜索.在现有累积时间价值向量基础上,执行1次运量全无全有加载,得到新的路段流量{yna}.
Step 4“相继平移”移动.∀a
Step 5检查收敛性.计算取后3次的路段平均流量构造收敛判断函数,即时算法终止,ε为收敛指标.否则转Step6.
Step 6迭代次数判断.迭代次数n>Nmax时算法终止,Nmax为最大迭代次数;否则,转Step2,置n=n+1.
4 数值算例
本文提出的考虑路网通行能力退化和用户风险偏好的双参考点网络均衡模型可以用于分析以下关键参数之间的关系:①路网能力退化程度,②用户风险态度,③网络均衡流量分布,④不同路径出行最佳到达时间参考点,⑤最早正效用时间参考点,⑥均衡时累积达到时间价值,⑦均衡时路网时间期望和标准差等.由于以上关键参数在同一个模型中相互影响,为明确参数间的关系,必须将其他影响因素简化.因此,本文采用交通网络均衡分析中常用的两路段基础网络(图1)作为分析对象.模型中具体参数设置如下:BPR路段时间模型中Q=500、t0a=[100,150]、λ=0.15、β=4、γ=1.5、Tˉ=222、σ=0.8、ϑ=[0.69,0.69,0.74,0.74]、τ=[-2.25,1,2.538 9,-5.712 5]、α=[0.52,0.52,0.52,0.52].模型内生重要参数有路网时间期望和标准差、最佳到达时间参考点、最早正效用时间参考点、累积到达时间价值,以及均衡时的路段流量分布.

图1 测试路网图Fig.1 Road network
4.1 路网均衡性检验
下面对路网均衡稳定性进行讨论.图2节选了路网能力保有系数θ∈[0.47,0.49]时,路网流量均衡过程.显然,在不同退化系数下,路网流量均可达到稳定均衡状态.
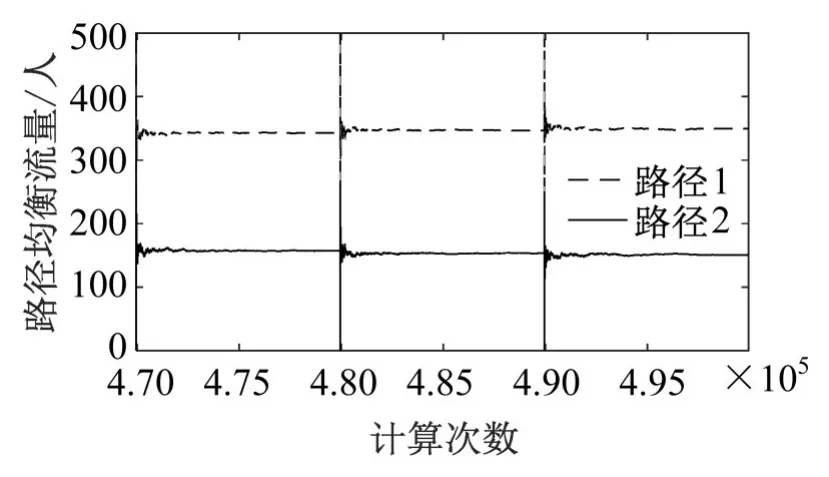
图2 路网均衡稳定性测试图Fig.2 User equilibrium convergence procedure
4.2 路网通行能力保有系数与路段设计能力参数取值范围
经实验发现,路网能力保有系数θ和路网设计能力对路网时间期望和标准差、最佳到达时间参考点、最早正效用时间参考点、累积到达时间价值,以及均衡时的路段流量分布等重要参数产生显著影响.这是因为决定了稳定时期路网通行时间上限,均匀分布的θ决定了路段通行能力的下限,当θ取值较小时,说明该路段可能发生无法通行的极端情况,使得该路段时间期望和标准差取值非常大.在此情况下,巨大期望说明该路段已经无法通行,巨大标准差说明该路段通行能力无法预测,因而失去了研究的必要性.同时,θ较大时,说明该路段通行能力几乎不受影响,此时路段时间期望等于零流时间,标准差接近于零.虽然理论上路网保有能力系数取值范围为[0,1],但根据本文测试数据,时,时间期望、时间标准差因此,为提高研究的现实意义,对的取值范围进行讨论.
根据实际路网测试数据,当用户考虑出行路径时,会以工作开始时间和路段零流时间作为重要参考数据,因此有效路段时间和期望不能与以上2个参数相差太远.在参考相关研究[3,5-6,8]后,本文以出行作为讨论区间,选择因此,为提高研相应适当的保有系数和路段设计能力上限.经计算可行区域如图3所示.
4.3 路网能力保有系数对其他重要参数的影响
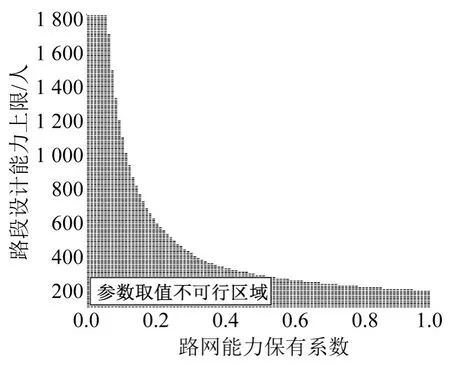
图3 路网能力保有系数与路段设计能力上限取值范围Fig.3 Value range of two important parameters
(1)当θ∈[0.30,0.33]时,随着θ增加:
①各路径时间期望缓慢下降,且路径1稳定性小于路径2;
②各路径时间标准差迅速下降,且路径1的标准差显著大于路径2,例如θ∈[0.30,0.33]时,
③2条路径最佳到达时间参考点和最早到达时间参考点取值均稳定下降;
④2条路径到达时间感知价值迅速上升,且曲线基本重合;
⑤2条路径均衡流量非常稳定,分别为265和235左右.
以上参数曲线变化说明,虽然路径1时间期望显著小于路径2,但其标准差显著大于路径2,此时用户择路并不仅希望期望时间较短,也考虑了出行时间不确定性.因此均衡时2条路径流量基本相当.由于2条路径不确定性均较大,因此2条路径到达时间感知价值Vr,kATP显著小于0,但随着路网能力下限改善,不确定性下降,2条路径Vr,kATP迅速上升,并稳定在10左右.
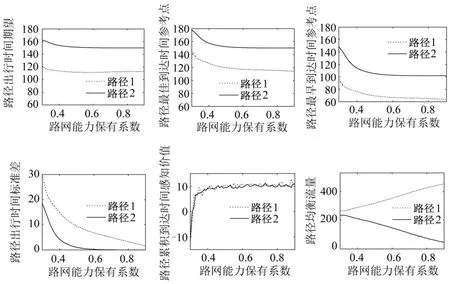
图4θ∈[0.3,0.9]、a=[500,550]时的路网均衡状态Fig.4 Important parameters in user equilibrium with deferentθ
(2)θ∈[0.33,0.90]时,随着θ增加:
①2条路径时间期望基本保持稳定,而路径1时间期望显著小于路径2;
③2条路径最佳到达时间参考点和最早到达时间参考点取值稳定,曲线形状与路径时间期望相似;
④路径1均衡流量稳定上升至454,路径2稳定下降至46.
以上参数曲线变化说明,随着路网能力退化下限继续改善,2条路径出行时间不确定性持续下降.此时,路径1出行时间期望显著快于路径2,但存在一定不确定性,而路径2不确定性非常小.因此,虽然路径1期望略快,但为了保证准时到达的可靠性,仍有部分出行者选择不确定性很小的路径1出行.不过随着路径1与路径2不确定性逐渐接近,更多出行者由路径2转向路径1.在这一阶段,由于路网不确定性可控,用户到达累积时间价值维持在10左右,且VA1TP≈VATP2,此时网络保持均衡状态.这不仅满足交通网络均衡条件,也印证了本文以累积到达时间感知价值最大作为择路规则的基本假设.
5 结论
本文基于连续分布的路网能力退化下限,构造随机路段时间分布期望和方差、设置累积到达时间价值函数的连续双参考点,并以累积到达时间价值最大作为择路准则,构建了用户均衡模型,对解的存在性进行了证明.最后用算例分析了路网能力退化下限和路段设计能力上限等模型重要外生参数的取值范围,讨论了用户均衡时路网能力退化下限对路径时间期望、标准差、最佳到达时间参考点、最早到达时间参考点、累积到达时间价值和路网均衡流量分布的影响.本文首次将客观路网能力退化下限与主观累积到达时间双参考点标定联系起来,对于探索有限理性下出行行为对交通网络的影响具有一定意义.
