基于Vine Copula的原油海运网络中节点连通可靠性研究

王 爽，吕 靖，赖成寿

(大连海事大学交通运输工程学院，辽宁大连116026)

0 引言

原油海运网络是原油运输的重要载体，原油海运网络中关键节点的连通状况会影响原油的安全运输.而原油海运网络中关键节点的连通性受恶劣天气、船舶交通事故、海盗及海上恐怖主义、节点隶属国家政局不稳定及军事冲突等突发事件影响，且各突发事件之间存在相关关系，共同影响节点的连通性.如恶劣天气很有可能增加发生船舶交通事故的可能性；在政局不稳定及存在军事冲突的地区船舶遭受海盗袭击的可能性会增加.研究各突发事件相互关联时的原油海运网络中关键节点的连通可靠性，对优化进口原油海运路径选择，保障进口原油运输安全具有重要意义.

连通可靠性的概念由日本学者Mine等于1982年提出，它反映的是交通网络两节点之间保持连通的概率，一般只研究路段的0和1两种状态，即连通或不连通[1].在Mine的基础上，Iida等将两点之间的连通性扩展到k点及整个网络的可靠性[2].分析连通可靠性的解析方法主要包括最小路/割算法[3]，其计算复杂度随网络节点数增加而指数增长，Wakayabashi[4]利用布尔代数，通过Esary-Proschan上下边界法评估连通可靠性，简化了计算.

Copula函数的概念由Sklar于1959年提出，它是将各单变量边缘分布与联合分布连接起来的函数，使得边缘分布和联合分布函数的选择更加灵活[5].Copula函数被广泛应用于许多领域的相关关系建模中[6-7]，但当维数增加时，copula的参数估计变得困难，因此 Joe[8]，Bedford[9]，Aas[10]等提出并发展了vine copula.Vine copula通过将高维copula分解成一系列成对二元copula的乘积来简化高维数据联合分布的构建.Vine copula广泛应用于金融、水文等领域[11-12].

综上可知，连通可靠性的研究主要集中于城市道路网络等陆上交通网络，关于海运网络连通可靠性的研究较少，而vine copula函数能较好地描述变量间的相关关系，因此本文基于vine copula函数构建各突发事件的联合分布，从而分析各突发事件相互关联时的原油海运网络中关键节点的连通可靠性，为优化原油海运路径选择提供依据.

1 问题描述

根据国际海事组织全球综合航运信息系统(GISIS)数据库的统计，影响海运网络中节点连通性的突发事件主要包括恶劣天气、交通事故、海盗及海上恐怖主义、节点隶属国家政局不稳定及军事冲突.而且这些突发事件间存在相关关系，一种突发事件的发生往往会对其他突发事件的发生产生影响.例如，恶劣天气时船舶发生交通事故的概率很有可能提高；良好的天气、海况是海盗活动成功的保障因素，因此恶劣天气时发生海盗袭击的可能性会降低；在政局不稳定或存在军事冲突的地区，遭受海盗袭击的可能性会提高，如索马里.这些相互关联的突发事件共同影响节点的连通可靠性.

本文的研究目的是要确定各突发事件相互关联时的原油海运网络中关键节点的连通可靠性，为优化原油运输路径提供支持.不同突发事件相互关联时的原油海运网络中关键节点连通可靠性属于多维联合概率问题，令X=(X1,X2,…,Xd)表示各突发事件，即通过求各突发事件的联合分布F=F(x1,…,xd)=P{X1≤x1,X2≤x2,…,Xd≤xd} ，进而计算各关键节点的连通可靠性.

2 原油海运网络中关键节点连通可靠性度量的vine copula模型构建

Vine copula函数能较好地求解上述存在相关关系的多变量联合概率问题，通过vine copula函数，多维联合概率密度函数可以分解为一系列二元copula概率密度函数的乘积.其中二元copula函数有多种类型可选择，可采用拟合优度检验方法择优.基于最优的vine copula函数构建的联合分布，可以计算各关键节点的连通可靠性.

2.1 基于高斯混合模型的突发事件边缘分布估计

建立vine copula函数的前提是估计各突发事件的边缘分布.高斯混合模型是用有限个高斯密度函数的线性组合来估计随机变量的概率密度分布，如果高斯分布的个数足够多，通过调整线性组合的权重系数及每个高斯分布的数字特征，可以精确描述任何连续随机变量的概率密度分布.因此本文使用高斯混合模型来估计各突发事件的边缘分布.

各突发事件的边缘分布可以表示为

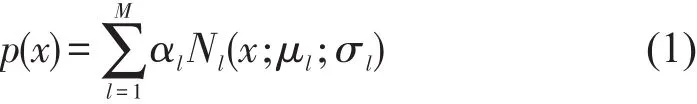
式中：x是各突发事件的一维观测值；M为高斯混合模型的阶数；αl(l=1,2,…,M)是高斯混合模型中子高斯分布的权重，满足

Nl(x;μl;σl)(l=1,2,…,M)是高斯分布，可以表示为

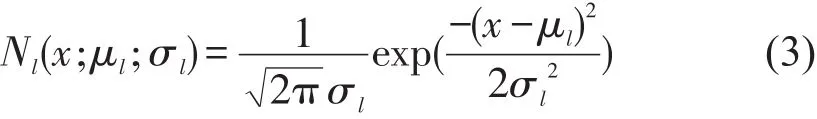
式中：μl,σl分别为第l个高斯分布的均值和方差.αl,μl,σl为待估参数，本文采用EM算法估计高斯混合模型中的参数.

2.2 关键节点连通可靠性度量的vine copula模型构建

Copula是指“连接”多维随机变量的联合分布和边缘分布的函数，它可以将一个联合分布分解为它的k个边际分布和一个copula函数，其中的copula函数形式描述了变量间的相关结构[5].

根据Sklar定理：令恶劣天气、交通事故、海盗及海上恐怖主义、节点隶属国家政局不稳定及军事冲突等突发事件的联合分布为F=F(x1,…,xd)，边缘分布分别为F1=F1(x1),…,Fd(xd)，则存在1个Copula函数C，使得

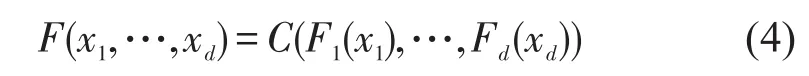
对于拥有连续且严格递增边缘分布的联合分布函数F，联合概率密度函数f可表示为

Vine copula可以将式(5)分解为d(d-1)/2个二元copula密度函数[10]，vine copula有两种比较常用的形式，分别为C-vines和D-vines.C-vines适用于多变量间存在明显的引导变量的情况，不存在明显的引导变量时D-vines更适用.本文不存在一个突发事件引导另一个或两个突发事件的情况，因此选择D-vines copula分解式(5)[9].

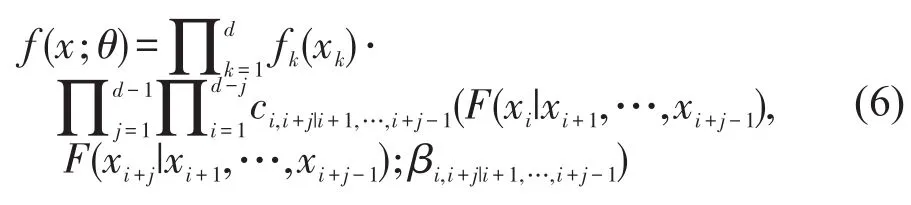
式中：fk(xk)是突发事件的边缘概率密度函数；ci,i+j|i+1,…,i+j-1是二元copula的概率密度函数；βi,i+j|i+1,…,i+j-1为参数；θ为所有参数的集合.

在上述vine copula的构建过程中包含了边缘条件分布F(x|v)，Joe[8]指出

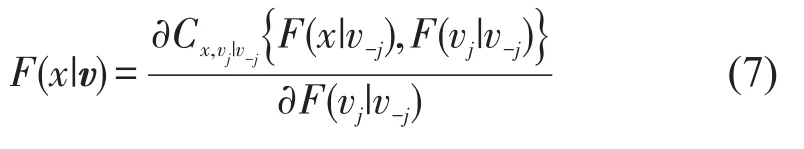
式中：vj是向量v的任意一个分量；v-j是向量v除去vj后的分量；Cx,vj|v-j表示二元copula条件分布函数.特别的当v是单变量时有

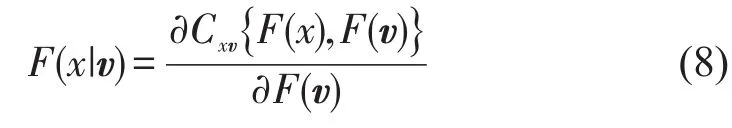
当x和v是均匀分布，即f(x)=f(v)=1，F(x)=x，F(v)=v时，h(x,v,Θ)可以用来表示这一条件分布函数，即有

式中：Θ为参数集合.

在进行D-vine copula结构选择时，本文通过计算两两变量间的秩相关系数Kendall’sτ，选择令每一层的τ值绝对值总和最大的结构[10].式(6)中的二元copula不需要是同一类型，需要选择能最优刻画每对突发事件相关关系的copula.本文分别选择Gaussian,Student,Frank,Clayton及Gumbel copula这5种类型的二元copula来刻画突发事件间的相关关系.并采用逐步半参数法(Stepwise Semiparametric Estimators)估计D-vine copula的参数[10].本文采用基于经验copula的Cramér-von Mises统计量进行拟合优度检验[13].

3 实证分析

3.1 数据选取及处理

本文选择马六甲海峡进行案例分析.马六甲海峡是原油海运网络中最重要的战略节点，其连通可靠性的评估对原油海上运输安全至关重要.由于恶劣天气时海面风速较大，因此本文中的恶劣天气用海面风速表示，海面风速数据来源于Remote Sensing Systems(http://www.remss.com).节点隶属国家政局不稳定及军事冲突情况用国家风险指数(International Country Risk Guide)表示，该风险指数由PRS集团发布(https://www.prsgroup.com/).对于马六甲海峡，其隶属国家包括新加坡、马来西亚和印度尼西亚，因此马六甲海峡的隶属国家政局不稳定及军事冲突情况用上述3个国家风险指数的平均值表示.海盗及海上恐怖主义用海盗及持械抢劫数量表示，它和船舶事故数据均来源于国际海事组织的全球综合航运信息系统(GISIS)数据库.

由于海盗和船舶事故并不总是同时发生，因此本文将突发事件分成两种情形.情形1包括3种突发事件，分别是：海盗及持械抢劫数量，海盗及持械抢劫发生时的海面风速，以及国家风险指数；情形2也包括3种突发事件，分别是：船舶事故数量、船舶事故发生时的海面风速及国家风险指数.本文收集了1993—2013年马六甲海峡发生的海盗及持械抢劫数、船舶事故数，新加坡、马来西亚和印度尼西亚国家风险指数及海面风速.其中海面风速指的是海盗及持械抢劫发生时或船舶事故发生时海面风速的年度平均值.本文分别评价了情形1和情形2中突发事件相互关联时的马六甲海峡的连通可靠性.

3.2 结果及结果分析

3.2.1 突发事件边缘分布

影响马六甲海峡的各突发事件边缘分布的高斯混合模型参数估计值如表1所示.

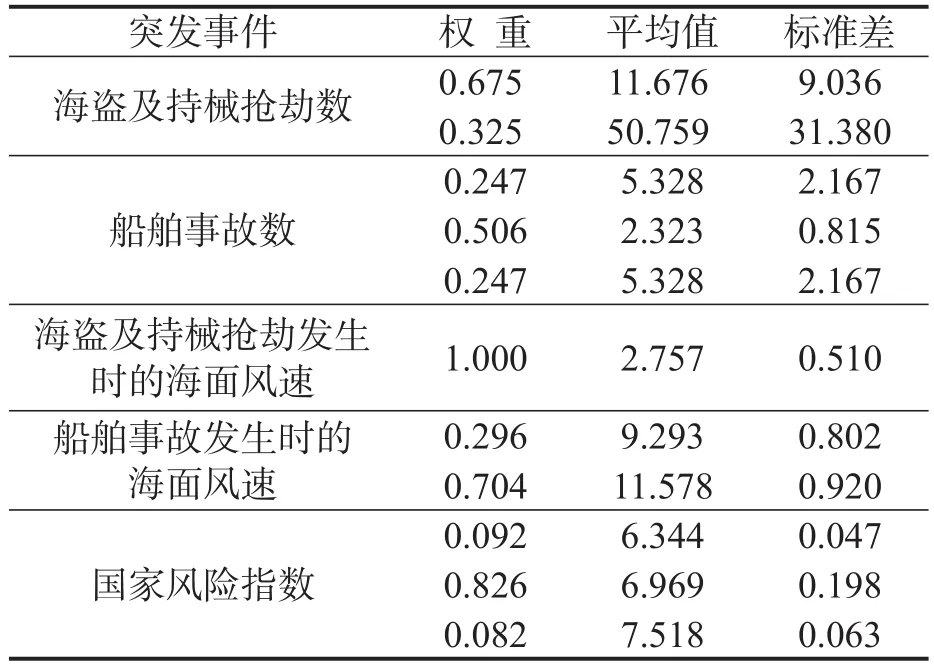
表1 突发事件边缘分布的参数估计Table 1 Parameter estimates of marginal distribution functions for extreme events

3.2.2 Vine copula结构选择及参数估计

估计各突发事件边缘分布函数之后，计算秩相关系数Kendall’sτ的值如表2和表3所示，Kendall’sτ表示各突发事件间的相关结构.从表2和表3可以看出，国家风险指数和海盗及持械抢劫数之间有较强的负相关关系，这是因为较高的国家风险指数表示国家的潜在风险较低，因此海盗及持械抢劫数量较少.平均海面风速与海盗及持械抢劫数及船舶事故数之间也存在相关关系.

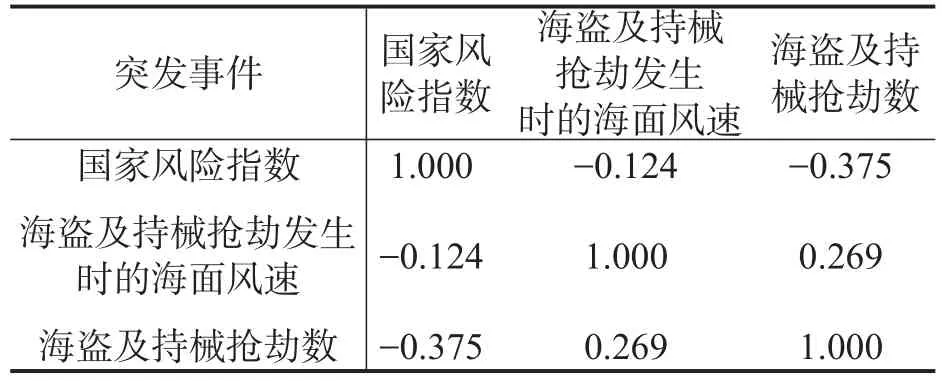
表2 各突发事件秩相关系数矩阵(情形1)Table 2 Kendall’s Tau dependence matrix of extreme events in Scenario 1

表3 各突发事件秩相关系数矩阵(情形2)Table 3 Kendall’s Tau dependence matrix of extreme events in Scenario 2

根据表2和表3及D-vine copula的结构选择准则，情形1中三维D-vine copula变量的顺序为：国家风险指数(x1)，海盗及持械抢劫数(x2)及海盗及持械抢劫发生时的海面风速(x3).情形2中变量的顺序为：国家风险指数(y1)，船舶事故发生时的海面风速(y2)及船舶事故数(y3).采用逐步半参数法估计D-vine copula的参数，并根据AIC值选择最优的二元copula.情形1和2中三维D-vine copula包含的二元copula的类型及其参数如表4和表5所示.计算基于经验copula的Cramér-von Mises统计量Sn，进行拟合优度检验，如表6所示.

表4 三维D-vine copula的参数估计(情形1)Table 4 Parameter estimates of the 3-dimensional D-vine copula in Scenario 1

表5 三维D-vine copula的参数估计(情形2)Table 5 Parameter estimates of the 3-dimensional D-vine copula in Scenario 2

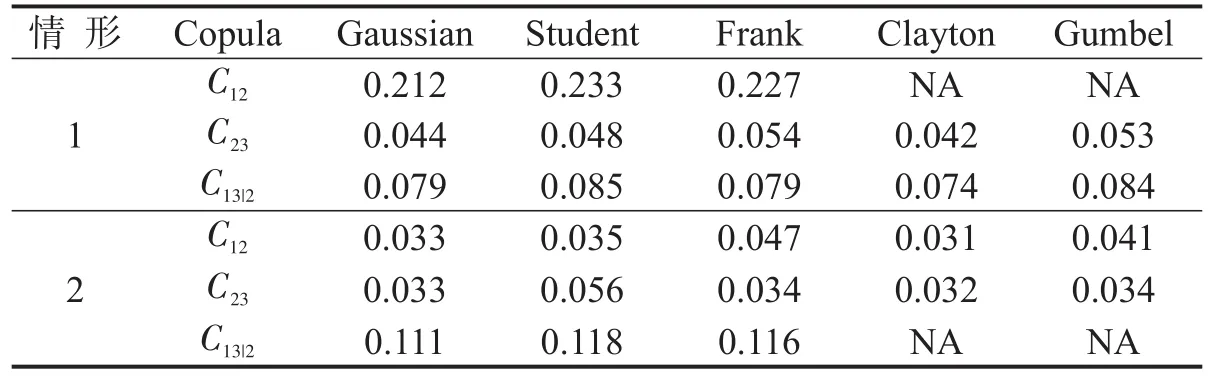
表6 拟合优度检验Table 6 Goodness-of-fit tests

Sn越小，拟合效果越好，因此由表6可以发现Sn的检验结果与根据AIC值选择的最优copula结果一致.

表4～表6表明，Gaussian和 Clayton copula在刻画两两突发事件相关关系上具有优势.这些二元copula的参数表明国家风险指数和海盗及持械抢劫数，以及海盗及持械抢劫数和海盗及持械抢劫发生时的海面风速间有较强的相关性.而船舶事故数与船舶事故发生时的海面风速，以及在海盗及持械抢劫数条件下，国家风险指数与海盗及持械抢劫发生时的海面风速间的局部相关性相对较弱.

此外，由于Gaussian copula用来刻画变量间对称的尾部相关性，由此可知国家风险指数与海盗及持械抢劫数之间具有对称的尾部相关性，即无论国家风险指数增加还是减少，只要变化的绝对值相等，他们之间的相关程度就相同.而Clayton copula对变量在分布下尾部的变化很敏感，因此可以发现海盗及持械抢劫数与海盗及持械抢劫发生时的海面风速，船舶事故数与船舶事故发生时的海面风速间具有下尾相关性.即当海面风速降低时，海盗及持械抢劫数和船舶事故数减少的可能性会明显增加，此时他们间的相依关系很可能会增强.通过对各突发事件相关关系的分析，进而可以计算各突发事件相互关联时的节点连通可靠性.

3.2.3 连通可靠性分析

根据式(6)可知，由估计出的各二维copula的参数、边缘条件分布及边缘分布求解各突发事件的联合概率密度，进而求解联合分布、计算联合概率是十分困难的.由于海盗及持械抢劫和船舶事故是影响节点连通可靠性最直接的突发事件，而且由上面的分析可知海面风速及国家风险状况会对海盗及持械抢劫和船舶事故的发生产生影响，因此本文将给定海面风速及国家风险指数时，海盗及持械抢劫数和船舶事故数的条件概率作为马六甲海峡的连通可靠性.

基于上面建立的vine copula，可以获得条件分布函数，进而可以分析马六甲海峡的连通可靠性.给定国家风险指数和海面风速的值，海盗及持械抢劫数的条件分布可以表示为F(x2|x1,x3)，根据式(7)～式(9)，条件分布F(x2|x1,x3)可以表示为

也可以表示为

类似的，给定国家风险指数和海面风速值，船舶事故数的条件分布F(y3|y1,y2)可以表示为

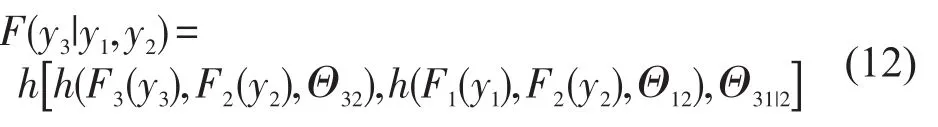
基于vine copula的参数估计值，可以求出F(x2|x1,x3)和F(y3|y1,y2).本文选择各突发事件2013年的取值，计算条件概率，即马六甲海峡的连通可靠性.给定x1=6.875 0，x3=3.234 4，计算得P(x2≤20|x1=6.875 0,x3=3.234 4)=0.239 5.同样的，给定y1=6.875 0，y2=10.820 6，计算得P(y3≤ 9|y1=6.875 0,y2=10.820 6)=0.906 1.可以看出在节点隶属国家政局不稳定及军事冲突、恶劣天气和海盗及海上恐怖主义的作用下，马六甲海峡的连通可靠性较低，仅为0.239 5；而在节点隶属国家政局不稳定及军事冲突、恶劣天气和船舶交通事故的作用下，马六甲海峡的连通可靠性相对较高，为0.906 1.

4 结论

本文引入vine copula刻画各突发事件间的相关关系，建立突发事件的联合分布，并基于各突发事件的联合分布和条件分布进行节点连通可靠性分析，本文以马六甲海峡为例进行案例分析.结果表明，节点隶属国家政局不稳定及军事冲突与海盗及海上恐怖主义间具有对称的尾部相关性，而海盗及海上恐怖主义和船舶交通事故分别在恶劣天气转好时与其具有更强的相关性，即具有下尾相关性.此外，在节点隶属国家政局不稳定及军事冲突、恶劣天气、海盗及海上恐怖主义的作用下马六甲海峡的连通可靠性较低，仅为0.239 5；而在节点隶属国家政局不稳定及军事冲突、恶劣天气、船舶交通事故的作用下马六甲海峡的连通可靠性相对较高，研究结果可以为制定原油海上运输策略提供依据.