η凸函数的Riemann-Liouville分数阶积分的Hermite-Hadamard型不等式
2018-09-10时统业曾志红曹俊飞
时统业,曾志红,曹俊飞
(1. 海军指挥学院, 江苏 南京 211800; 2. 广东第二师范学院 学报编辑部, 广东 广州 510303;3. 广东第二师范学院 数学系, 广东 广州 510303)
0 引 言
若f是区间[a,b]上的凸函数,则对f在区间[a,b]上的算术平均值有以下估计:
(1)
双边不等式(1)被称为Hermite-Hadamard不等式.关于Hermite-Hadamard不等式的各种改进、加细和推广,可参见文献[1-9].
最近,作为通常凸函数的推广,文献[10]引入了η凸函数的概念.
定义1[10]设区间I⊆R,二元函数η:R×R→R,f:I→R,若对任意x,y∈I,t∈[0,1],有
f(tx+(1-t)y)≤f(y)+tη(f(x),f(y)),
则称f是区间I上的η凸函数.
当η(x,y)=x-y时,η凸函数即为通常的凸函数.
定理1[11](η凸函数的Hermite-Hadamard型不等式) 若f: [a,b]→R是η凸函数,η在f([a,b])×f([a,b])上有上界Mη,则有

近年来,国内外研究者利用分数阶积分建立了分数阶的Hermite-Hadamard型不等式[12-18].
定义2设α>0,f在[a,b]上勒贝格可积,则函数f的α阶左Riemann-Liouville分数阶积分和α阶右Riemann-Liouville分数阶积分分别定义为
其中Γ(α)是Gamma函数,即
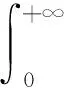
方便起见,在下文的引理和定理中均假设
p∈(0,1),ξ=pa+(1-p)b,
并且记

定理3[19](η凸函数的Hermite-Hadamard型分数阶积分不等式) 若f: [a,b]→R是η凸函数,η在f([a,b])×f([a,b])上有上界Mη,α>0,则有
(2)
引理1[13]设f: [a,b]→R在(a,b)可微,f′在[a,b]上勒贝格可积,α>0,则有
利用引理1,由文献[19]可得η凸函数的Hermite-Hadamard型分数阶积分不等式.
定理4[19]设f: [a,b]→R在(a,b)可微,|f′|是[a,b]上的η凸函数,α>0,则有
当η(x,y)=x-y,即当|f′|是[a,b]上的凸函数时,由定理4得到文献[13]中凸函数的Hermite-Hadamard型分数阶积分不等式.
引理2[14]设f: [a,b]→R在(a,b)可微,f′在[a,b]上勒贝格可积,α>0,则有
其中,
应用引理2,由文献[19]可得到η凸函数的Hermite-Hadamard型分数阶积分不等式.
定理5[19]设f: [a,b]→R在(a,b)可微,|f′|是[a,b]上的η凸函数,0<α≤1,则有
η(|f′(a)|,|f′(b)|)+η(|f′(b)|,|f′(a)|)].
(3)
由引理2并利用积分变量代换,有
可得到以下引理:
引理3设f: [a,b]→R在(a,b)可微,f′在[a,b]上勒贝格可积,α>0,则有
[f′((1-t)a+tb)-f′(ta+(1-t)b)]dt.
目前,国内研究η凸函数的文献并不多[20-21].本文建立了新的η凸函数Hermite-Hadamard型分数阶积分不等式.对定理3和定理5的结果进行了一定改进.对由凸函数分数阶的Hermite-Hadamard型不等式的右边部分生成的差值,给出了不同于定理4的估计.为证明主要结论,除引理1和引理3外,还需要引理4和引理5,此两引理用分部积分法易证之.
引理4设f: [a,b]→R在(a,b)可微,f′在[a,b]上勒贝格可积,α>0,则有

引理5设f: [a,b]→R在(a,b)上可微,f′在[a,b]上勒贝格可积,α>0,则有
pf(a)+(1-p)f(b)-K2=
1 主要结果及证明
定理6若f: [a,b]→R是η凸函数,η在f([a,b])×f([a,b])上有上界Mη,α>0,则有
(4)
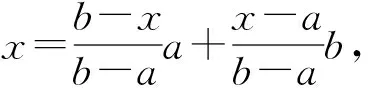
(5)
(6)

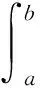
[η(f(a),f(b))+η(f(b),f(a))],
(7)
由η凸函数的定义,有
(8)
将式(8)乘以(x-a)α-1+(b-x)α-1,然后在[a,b]上对x积分,得

η(f(a+b-x),f(x))dx,
(9)

注2在定理6中,取η(x,y)=x-y,则得到凸函数的Hermite-Hadamard型分数阶不等式[13]:
文献[3]利用积分给出了凸函数的Jensen不等式的隔离,受此启发,给出以下定理:
定理7若f: [a,b]→R是η凸函数,α>0,则有
[η(f(a),f(b))+η(f(b),f(a))],
(10)
其中,
f1(x)=η(f(b-p(x-a)),f(pa+(1-p)x)),
f2(x)=η(f(a+(1-p)(b-x)),f(px+(1-p)b)).
证明将式(5)乘以(ξ-x)α-1,然后在[a,ξ]上对x积分,得
(11)
将式(6)乘以(x-ξ)α-1,然后在[ξ,b]上对x积分,得
(12)

f(ξ)≤f(x)+(1-p)η(f(y),f(x)),
(13)
将式(13)乘以(ξ-x)α-1,然后在[a,ξ]上对x积分,得
(14)

f(ξ)≤f(x)+pη(f(y′),f(x)),
(15)
将式(15)乘以(x-ξ)α-1,然后在[ξ,b]上对x积分,得
(16)
推论1若f: [a,b]→R是η凸函数,η在f([a,b])×f([a,b])上有上界Mη,α>0,则有
f(ξ)-2p(1-p)Mη≤K2≤
定理8设f: [a,b]→R在(a,b)上可微,f′在[a,b]上勒贝格可积,|f′|是[a,b]上的η凸函数,α>0,则有
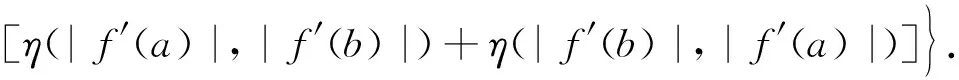
(17)
证明由引理1得
(18)
由|f′|的η凸性,得
|f′(ta+(1-t)b)|≤
|f′(a)|+(1-t)η(|f′(b)|,|f′(a)|),
(19)
|f′(ta+(1-t)b)|≤
|f′(b)|+tη(|f′(a)|,|f′(b)|),
(20)

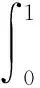

(21)
综合式(18)和(21),则式(17)获证.
注3在定理8中,若η(x,y)=x-y,即|f′|是[a,b]上的凸函数,则可得文献[13]的凸函数的Hermite-Hadamard型分数阶积分不等式.
定理9设f: [a,b]→R在(a,b)上可微,f′在[a,b]上勒贝格可积,|f′|是[a,b]上的η凸函数,0<α≤1,则有

(22)
证明由引理3得
[|f′((1-t)a+tb)|+|f′(ta+(1-t)b)|]dt.
(23)
由|f′|的η凸性得
|f′((1-t)a+tb)|≤
|f′(a)|+tη(|f′(b)|,|f′(a)|),
|f′((1-t)a+tb)|≤
|f′(b)|+(1-t)η(|f′(a)|,|f′(b)|),
|f′(ta+(1-t)b)|≤
|f′(a)|+(1-t)η(|f′(b)|,|f′(a)|),
|f′(ta+(1-t)b)|≤|f′(b)|+tη(|f′(a)|,|f′(b)|),
将上面4个式子相加并除以2得
|f′((1-t)a+tb)|+|f′(ta+(1-t)b)|≤
η(|f′(b)|,|f′(a)|)).
(24)
综合式(23)和(24),则式(22)得证.

定理10设f: [a,b]→R在(a,b)上可微,f′在[a,b]上勒贝格可积,|f′|是[a,b]上的η凸函数,α>0,则有

(25)
证明由引理4得

(26)
由|f′|的η凸性得


(27)


η(|f′(b)|,|f′(a)|)]dt=
(28)
综合式(26)~式(28),则式(25)得证.
注5在定理10中,若η(x,y)=x-y,也即|f′|是[a,b]上的凸函数,则有
{[α+1+2(α+3)p]|f′(a)|+
[3α+7-2(α+3)p]|f′(b)|}.
定理11设f: [a,b]→R在(a,b)上可微,f′在[a,b]上勒贝格可积,|f′|是[a,b]上的η凸函数,α>0,则有

证明利用类似于引理5及定理9的证明方法可证得定理11,此证略.
推论2若f: [a,b]→R是η凸函数,f′在[a,b]上勒贝格可积,|f′|是[a,b]上的η凸函数,α>0,则有
[η(|f′(a)|,|f′(b)|)+η(|f′(b)|,|f′(a)|)].
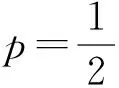
注6在定理11中,若η(x,y)=x-y,也即|f′|是[a,b]上的凸函数,则有
|pf(a)+(1-p)f(b)-K2|≤
2 结束语
建立了η凸函数的一些积分不等式,推广了通常凸函数的相应结果. 寻找积分隔离η凸函数的Jensen型不等式,以及利用导函数的η凸性进行误差估计,均仿照了通常凸函数的研究方法. 能对已有结果做些改进,得益于证明技巧的提升,包括分别在不同区间上对2个不等式积分,以及利用变量代换改变积分区间. 有关凸函数的其他结果在η凸函数上的移植尚待进一步研究.
