考虑再制造设计水平的多期闭环供应链网络均衡

张桂涛，曲箫宇,戴更新，胡劲松，王永波,3，孙 浩

(1.青岛大学自动化与电气工程学院，山东 青岛 266071；2.青岛大学商学院，山东 青岛 266071；3.空军青岛航空医学鉴定训练中心，山东 青岛 266071)

1 引言

由于全球环境恶化和资源短缺的出现，再制造和闭环供应链在学界和业界备受关注。再制造生产活动减少了对资源的需求，同时降低了废弃物产生量[1-3]，对环境的影响大大降低，从而有利于环保目标和可持续发展战略实现，因此再制造闭环供应链研究和实施具有重要意义。

再制造复印机与原材料生产的复印机相比，在材料、劳动力和能耗方面节省20%，废弃物减少35%[4]，对核心部件的回收和再利用能够节省大约40～60%的成本[5]。鉴于此，美国、欧盟和我国均采取立法的方式要求企业对产品进行回收和再制造[6]。在2015年的5月和9月，国务院出台和印发《关于加快推进生态文明建设的意见》、《生态文明体制改革总体方案》，在国家战略的高度上对资源回收和利用提出了具体要求。在该背景下，生产企业在实践中已纷纷开始进行再制造活动[7-9]。

同时，在新产品制造过程中，把产品设计成未来有利于再制造的样式，已经在一些企业中出现(业界称之为DFR， 即“Design for Remanufacturing”)，这其中包括施乐、柯达和通用等公司。如施乐提倡在产品的设计中，形成易拆卸、耐用和可再利用的理念[10]；柯达在高速复印机方面采用更贵的、可再次使用的不锈钢部件代替一些塑料部件[11]。随着再制造产业的发展，目前我国制造商亦逐步将其植入到产品的设计过程中[12]。Xu Zhizheng等[13]的研究考虑了政府对产品的监管，采用低碳多目标最优化设计产品来满足各方面的要求。Yang等[14]分析了早期的再制造设计对再制造过程的影响，并提出了一种基于模糊TOPSIS方法的设计支持工具以方便产品的再制造设计。

在产品设计阶段考虑其未来的可再制造水平，无疑会对制造商的产品生产策略、再制造过程乃至全球的资源可持续发展产生重要影响。正如Gehin等[15]所指出的，闭环供应链高效实施的一个重要方面是将来自于EOL策略的约束嵌入至早期的新产品设计中。但实际上，很多企业尤其是制造商对核心部件可再制造水平设计过程中应考虑哪些因素以及如何确定最优设计水平仍缺乏理论指导和有效的分析工具，从而导致其对DFR策略尚心存疑虑。BOSCH Tools管理者坦承需要更为专业的工具来做出更有效的再制造决策[16]。

另一方面，由于质量和可靠性方面的差异，消费者对新产品和再制造品的评价不同[17-20]，通常消费者对再制造品的评价相对较低。因此采用定量研究方法分析再制造活动对产品可再制造设计水平的影响以及消费者对新产品和再制造品的不同评价对闭环供应链定价策略的影响，不仅有助于企业决策者们消除疑虑，而且能够提高整个闭环供应链的系统绩效。已有文献的研究主要集中在链式供应链，亟待将有关研究拓展至考虑竞争的供应链网络。

此外，考虑到当前同类企业间竞争加剧，同时企业所在供应链间业务交叉，使供应链结构呈现为分层次的网络，包含众多企业和需求市场，企业间竞合关系共存，企业是理性决策者，目标是追求利润最大化。网络中同类成员间开展非合作竞争，并形成Nash均衡状态。如何获得该均衡条件是学界和业界关注的重要议题之一。目前绝大多数研究局限于单个制造商、单个零售商或单个回收商的闭环供应链，缺少对成员间竞争因素的分析，而竞争因素可能是企业从事再制造活动并获取利润的主要动力。少数学者针对制造商或者零售商内部存在竞争的闭环供应链网络展开研究。Nagurney和Toyasaki[21]利用变分不等式等理论建立了废旧电子产品的均衡模型。采用同样的理论方法，Hammond等[22]针对制造商和需求市场两层的闭环供应链网络建立均衡模型并对重点参数进行了灵敏度分析。Yang Guangfen等[23]则针对第三方回收模式建立了闭环供应链网络均衡模型，杨玉香等[24]在EPR制度下针对零售商回收模式建立了闭环供应链网络模型，与此相类似，本文的模型中废旧品回收也由零售商来承担。然而，文献[22-24]均是针对静态环境下闭环供应链网络均衡问题的研究。现实中供应链内部要素和外部环境不断发展变化，因此闭环供应链网络必然是一个动态系统，成员的最优决策也必然考虑到相关因素，如生产成本和市场需求等，在多个规划期的变化，此时决策者需通过相应的库存调整、前瞻性地对各期的产品可再制造水平进行动态决策来实现其多期总利润最大化。为描述该动态决策过程，本文拟将整个决策时间离散划分为多个规划期，假设某些参数在单个规划期内相对稳定，而相邻规划期之间则发生变化。Zhang等[25]构建了多规划期环境下的闭环供应链网络均衡模型，但该研究假设新产品和再制造品无差异，且未分析产品可再制造水平对再制造决策的影响。张桂涛等[26]结合双渠道闭环供应链网络，在多期决策环境下，研究了实体和电子交易渠道间存在竞争，消费者对两种渠道有不同偏好的供应链网络均衡问题。产品设计方面，Qiang Qiang[27]在2规划期框架下，探讨了考虑再制造设计水平的闭环供应链网络均衡问题，但其网络仅由制造商层和需求市场层构成，且未考虑多期决策中较为关键的库存调整策略，另外两期的再制造设计水平亦被假设完全相同。事实上，制造商的产品再制造设计水平具有明显的动态性，如在2期环境下，第1期要考虑到第2期的再制造成本等因素，而第2期即为最后1期，无需考虑其对未来的影响，因此2期的再制造设计水平显然不同。如前所述，市场中的消费者对新产品和再制造产品的评价不同，因而愿意支付的价格也存在差异，实际中消费者的需求是变化的，该因素也需要在动态模型中才能得以较为完整的描述。因此，针对闭环供应链网络，考虑消费者对两类产品的不同评价，在多期情形下研究具有竞争的网络成员的最优行为，以及由此达到供应链网络Nash均衡是非常有意义的。

在多个规划期环境下，在考虑同类成员竞争的基础上，针对制造商、零售商和需求市场组成的闭环供应链网络，其中政府规定最低的再制造设计水平，制造商可采取各期再制造设计水平相同和不同两种方案，并委托零售商回收需求市场的废旧品，对新产品和再制造品采用差异定价策略；零售商同时两种产品。通过变分不等式描述网络成员最优行为，重点分析网络成员均衡状态下再制造设计水平动态决策、新产品和再制造产品动态生产和定价决策，以及相邻规划期间的库存转移决策，以期为企业实践和生产运营决策提供理论支持。

2 问题描述与符号说明

2.1 问题描述

考虑一个多期闭环供应链网络，各制造商生产同质产品，网络成员包括M个制造商、N个零售商和K个需求市场。第1期采用原材料进行生产，为便于下一期的再制造，需对本期的产品可再制造设计水平进行决策；各制造商把产品批发给零售商销售，依据供需情况决策库存转移量；在第1期末，零售商把回收的废旧品销售给制造商，全部用于第2期的再制造生产活动中。在第1期，制造商把产品经各零售商销售给各需求市场，需求市场的消费者购买新产品并消费后产生废旧品，其中一部分由零售商负责回收，然后全部销售给制造商，用于其再制造活动。第2期往后，制造商一方面继续生产新产品并决策其可再制造设计水平，另一方面开展再制造活动，其再制造产品标有明显标识“再制造产品”，市场上的消费者对两种产品的评价不同，因此其批发价格也不同。制造商同时把新产品和再制造产品批发给零售商，并根据市场供需情况决定两种产品转移到下一期的库存量；零售商从各制造商处以不同价格批发新产品和再制造品，然后对两种产品分别定价，以差异化价格销售给消费者，期末回收废旧品；消费者对两种产品的评价不同，因而愿意支付的价格也不同。

对于研究的最后1个规划期，则不需考虑再制造设计水平对再制造成本的影响，且其前期生产的产品均需在最后1期销售完毕，因此最后1个规划期的决策情况与之前规划期的决策有明显的不同。

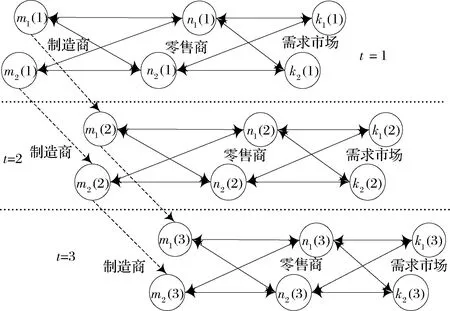
图1 包含三个规划期的闭环供应链网络

包含2制造商、2零售商、2需求市场，3个规划期的闭环供应链网络见图1。图中符号n1(2)表示第2个规划期的第1个零售商，其余符号可同样理解。下面对图1中交易和库存转移等活动进行说明。正向活动：从制造商到零售商的前向连线表示产品的批发，第1期只批发新产品，第2、3期同时批发新产品和再制造品；零售商与需求市场间的连线，从零售商指向需求市场方向表示产品的销售，第1期只销售新产品，第2、3期同时销售新产品和再制造品；逆向活动：从需求市场到零售商再到制造商是产品的回收过程；跨期活动：制造商在相邻规划期间的连线表示新产品跨期转移库存和废旧品的跨期使用。

为研究方便，给出以下假设：(1) 制造商生产过程中，由于使用废旧品可以节约成本，因此优先采用废旧品进行生产，该假设符合实际情况并与已有文献一致[23]；(2)文中涉及的生产与交易函数均为连续可微凸函数[24]；(3)销售的新产品只进行一次回收[26]，即只进行一次再制造；(4)假设各期的废旧品回收率相同(外生常量)，该假设可很容易地扩展到各期的回收率不同的情形[27]；(5)决策变量右上角的“*”表示该变量的最优值。

2.2 符号说明

t：某一规划期，t=1,2,…,T；

m：某一制造商，m=1,2,…,M；

n：某一零售商，n=1,2,…,N；

k：某一需求市场，k=1,2,…,K；

α：每期回收率；

ε：政府给零售商的单位回收补贴；

βv：原材料转化率；

βu：废旧品的可利用率；

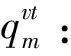
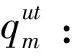
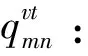
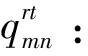
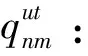
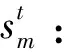
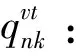
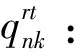
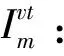
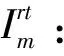
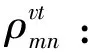
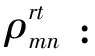
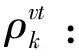
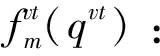
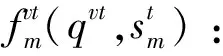
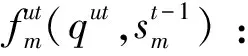
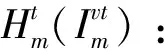
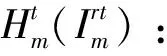
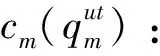
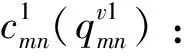
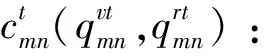
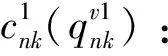
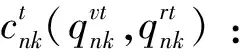
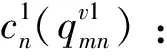
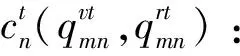
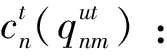
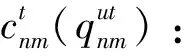
θk：需求市场k的消费者对再制造品的评价系数，θk∈(0,1]；

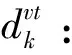
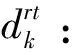
3 模型构建

3.1 制造商层的最优行为及其均衡

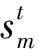
(1)

(2)

(3)

(4)

(5)

(6)

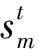
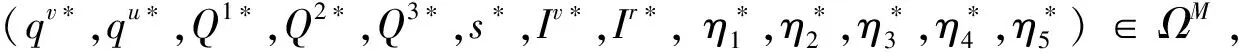
∀(qv,qu,Q1,Q2,Q3,s,Iv,Ir,η1,η2,η3,η4,η5)∈ΩM

(7)

其中

式(7)的第7项和第8项表明，制造商对两种情形的产品可再制造设计水平进行决策。

3.2 零售商层的最优行为及其均衡

根据市场供需状况，零售商在规划期初从制造商批发新产品和再制造品，并向消费者销售。在期末回收经消费者使用而产生的废旧品，其目标为实现其自身利润最大化，且其利润目标可表示为：

(8)

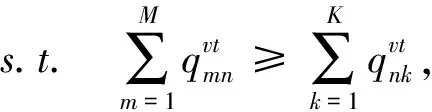
(9)

(10)

(11)

(12)

(13)

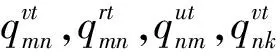
(14)

约束(9)和(10)表明，向各需求市场销售的新产品和再制造品数量应小于或等于其从各制造商批发的相应产品数量；约束(11)和(12)表明需求市场在各期的需求将得到满足；约束(13)表明零售商销售给各制造商的废旧品数量不能高于上一期销售给消费者的新产品数量乘以可回收因子α，α可解释为各需求市场产生废旧品的平均可回收比例；约束(14)说明决策变量非负。

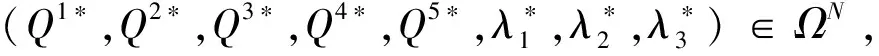
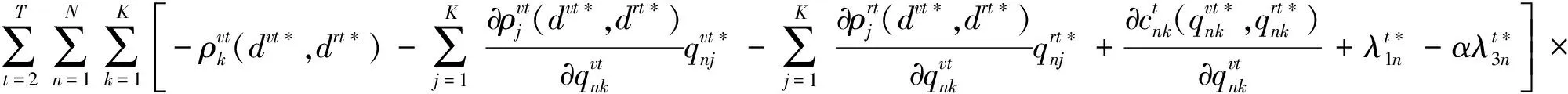
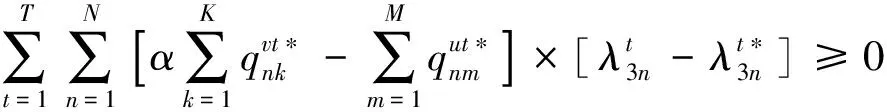
(15)

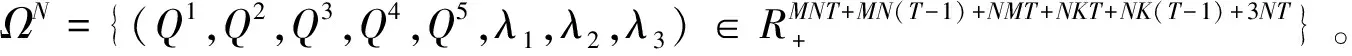
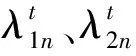
3.3 多期闭环网络均衡模型

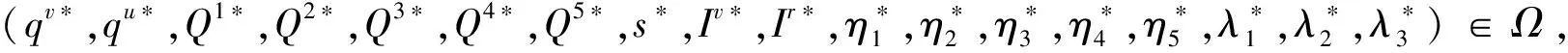
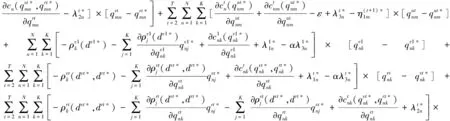
∀(qv,qu,Q1,Q2,Q3,Q4,Q5,s,Iv,Ir,η1,η2,η3,η4,η5,λ1,λ2,λ3)∈Ω

(16)

其中Ω=ΩM×ΩN。

各层决策者都达到Nash均衡状态时，供应链网络即达到Nash均衡状态，因此很有必要在凸规划条件下讨论解的存在性和唯一性，附录给出了式(16)解的性质有关证明。

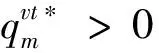
4 算例分析

算例采用图1所示的供应链网络结构和演化过程，3个规划期，每类成员各2个，在该供应链网络结构中，有决策变量96个。

本文采用修正投影收缩算法[29]求解。该算法设计简单，迭代步长固定，收敛快，能同时获得模型中26个Lagrange乘子，便于计算内生价格变量，可满足所建模型的求解要求。

基本参数：迭代步长为0.01，迭代终止条件为10-10，变量初值为[0.5]122×1的列向量。模型参数：α=0.3，ε=0.2，βv=0.95，βr=0.9。引入参数p1m、p2m分别表示制造商m在可再制造设计水平方面进行的投资对生产和再制造的影响因子，其值越大(小)表明单位投资对生产成本的影响越大(小)。其余函数形式如下：

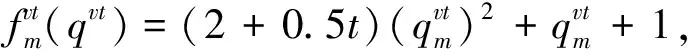
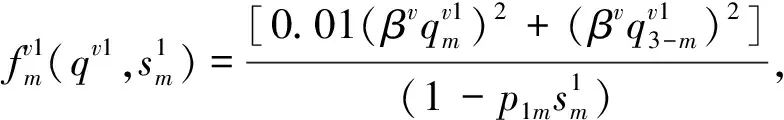
t=2,3, ∀m；

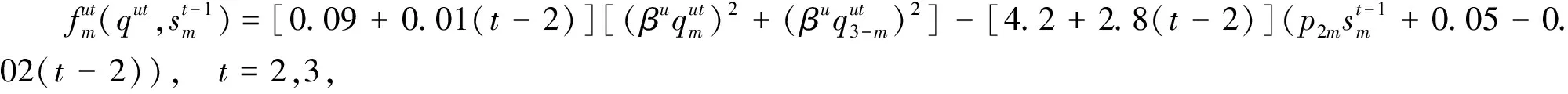
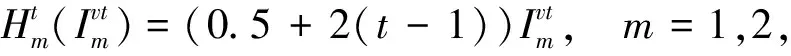
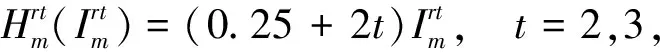
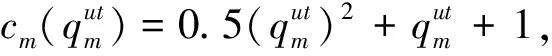
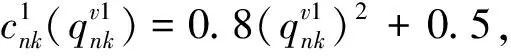
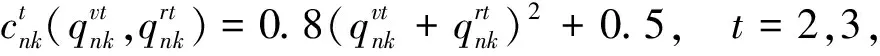
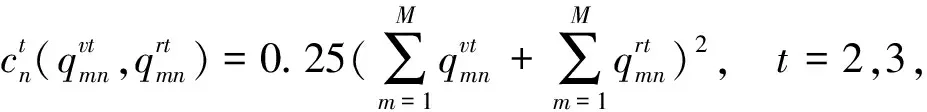
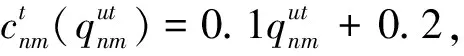
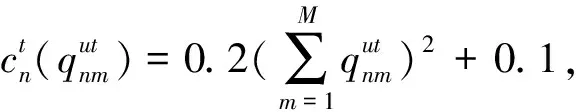
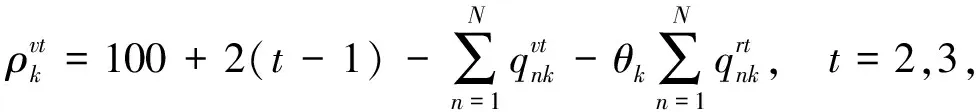
t=2,3, ∀k。

本文主要针对再制造投资影响因子对可再制造设计水平和企业利润的影响进行对比分析，并结合消费者对再制造品的评价系数、政府规定的最低可再制造设计水平等方面进行分析。具体而言，针对情况(1)p1m=1，p2m=0.6:0.2:1.6变化时的均衡状态，结果列于表1中；(2)p1m=1，消费者对再制造品的评价系数θk=0.2:0.05:0.8变化时，网络中制造商和零售商利润、制造商两种产品的生产量、库存、新产品可再制造设计水平等关键变量的变化走势如图2至图5所示；(3)sd=0.3，p1m=1，p2m=0.6:0.2:1.6变化时，制造商和零售商利润、制造商新产品可再制造设计水平等关键变量的变化走势图如图6、图7所示。

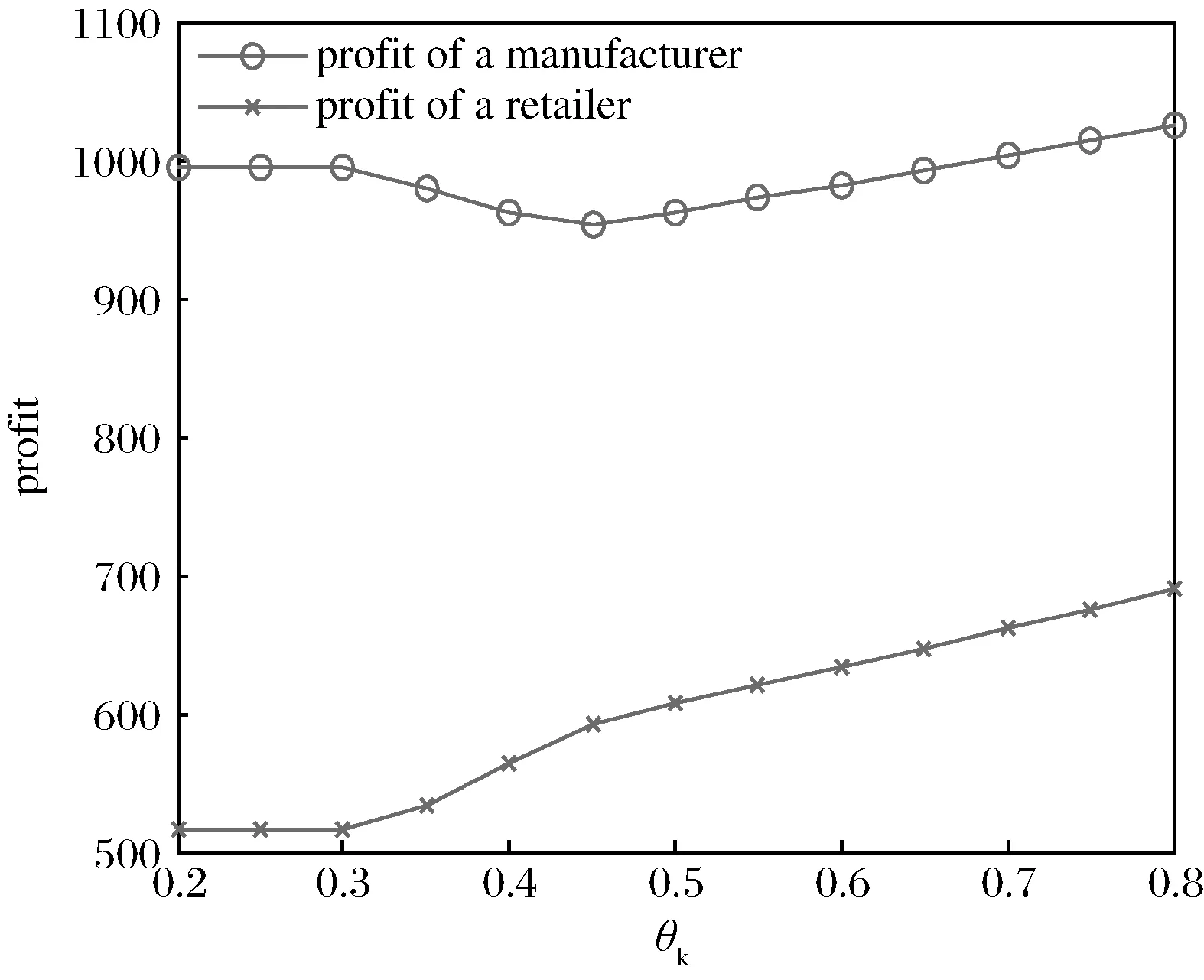
图2 制造商和零售商利润走势图

图3 产品生产量走势图

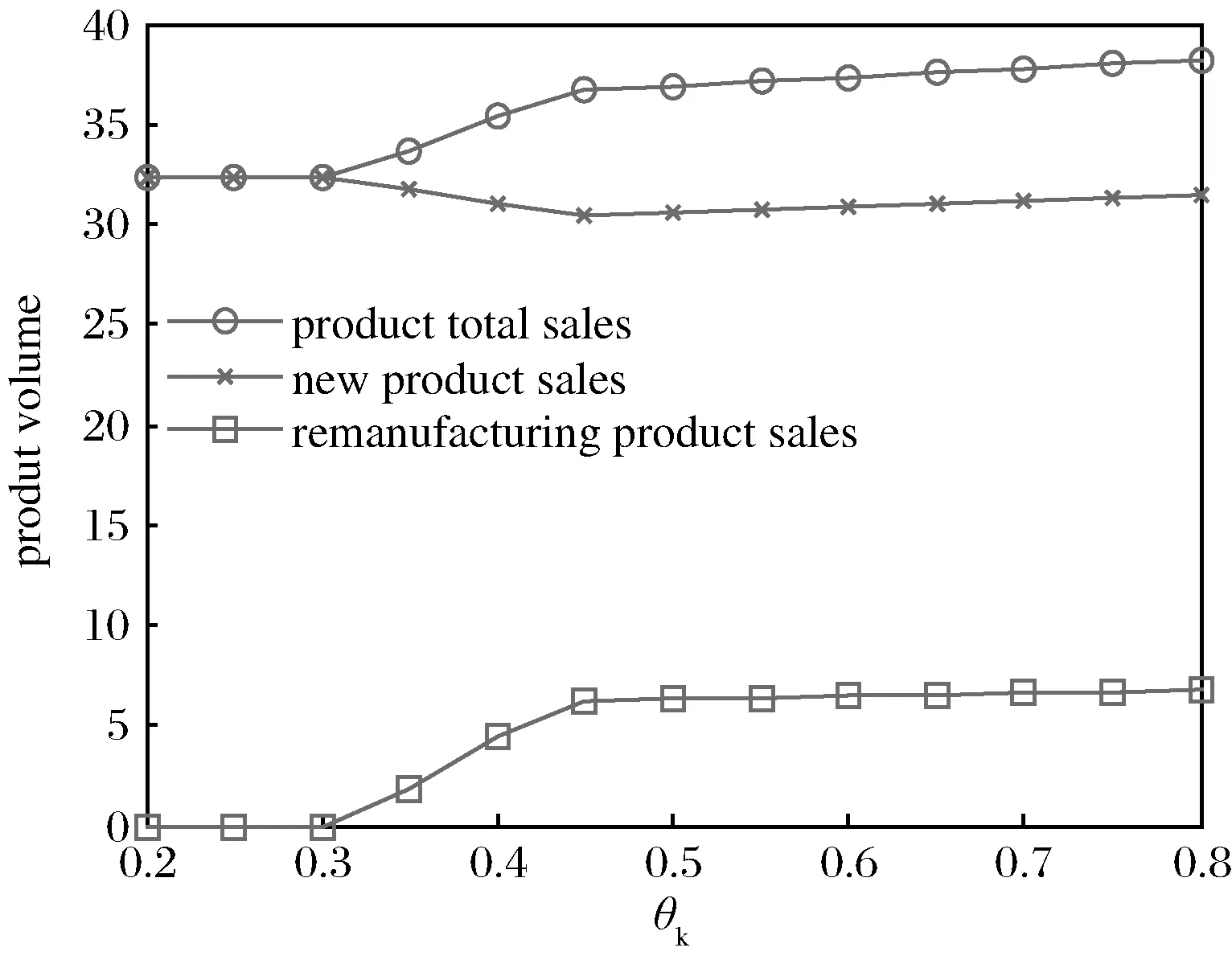
图4 产品库存量走势图

图5 可再制造设计水平走势图

图6 制造商可再制造设计水平走势图

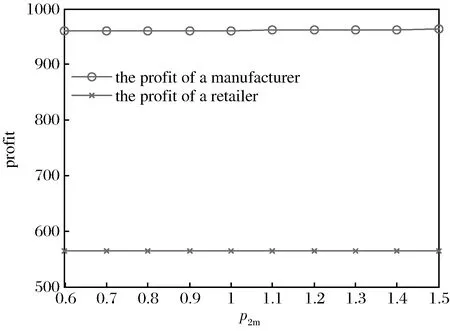
图7 制造商和零售商利润走势图

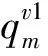
特别地，当p2m=0.6时，sm=0，说明此时再制造活动对制造商的作用不大，没有必要进行再制造设计。而随着p2m的增加，sm逐渐变大，说明制造商有必要进行再制造设计，且p2m越大，则越要提高再制造设计水平。

图2表明制造商利润在θk=0.3之前保持恒定，然后先减后增，最小值发生在θk=0.45附近；其原因为：当θk<0.3时，由于消费者对于再制造产品的认可程度太低，制造商根本无动机从事再制造；而当θk>0.3之后，再制造产品对新制造产品的蚕食程度已不容忽视，迫使制造商不得不进行产品的可再制造性投资(换言之，此时若制造商仍不从事再制造将将遭受更多的利润损失)，另由再制造成本的函数形式易知其开始时增加较快，导致在0.3<θk<0.45的区间里制造商从再制造产品中获得的收益无法弥补其成本的增加，因而利润减少；而随着θk

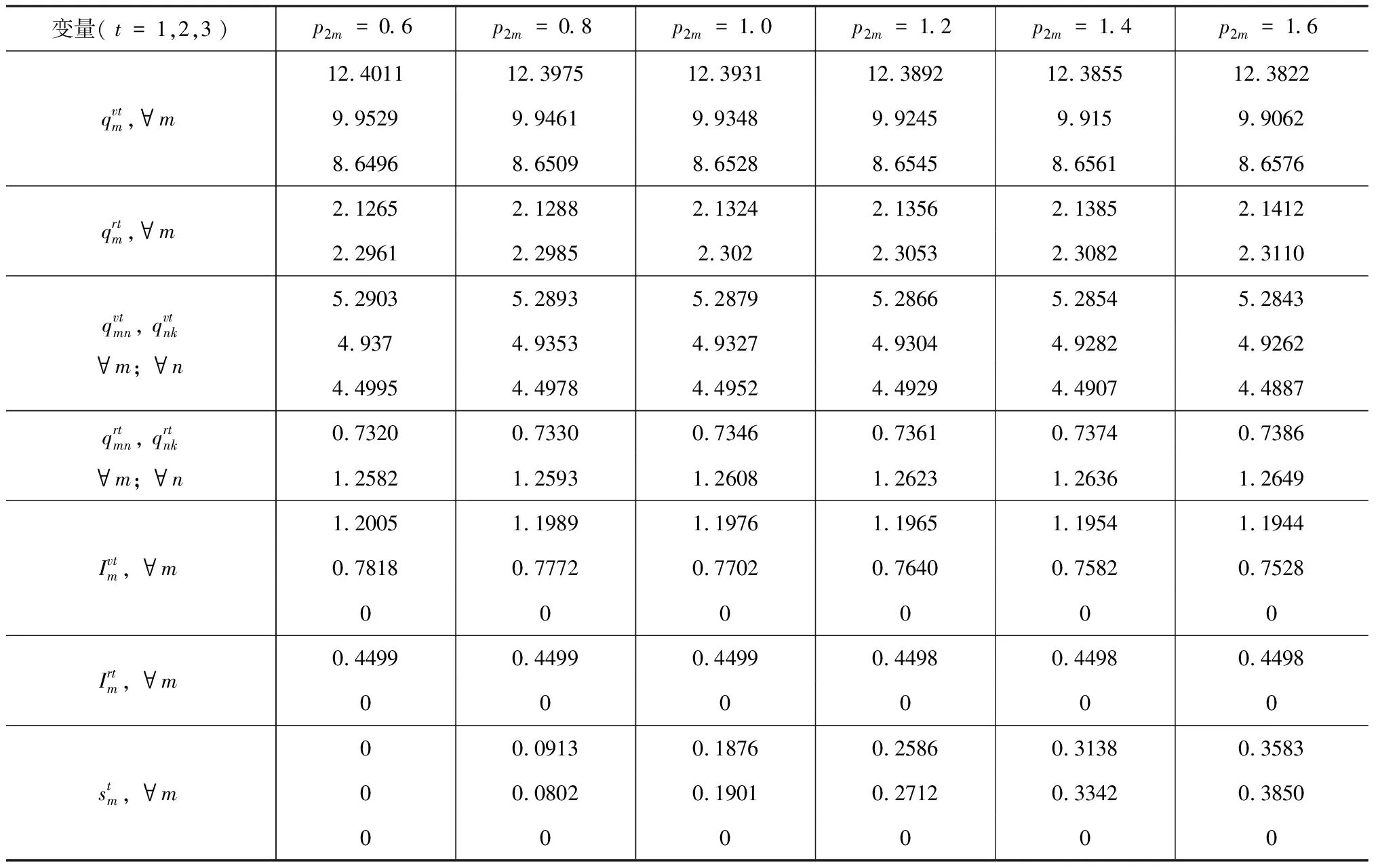
表1 考虑再制造设计水平的多期闭环供应链网络随p2m变化时的均衡结果

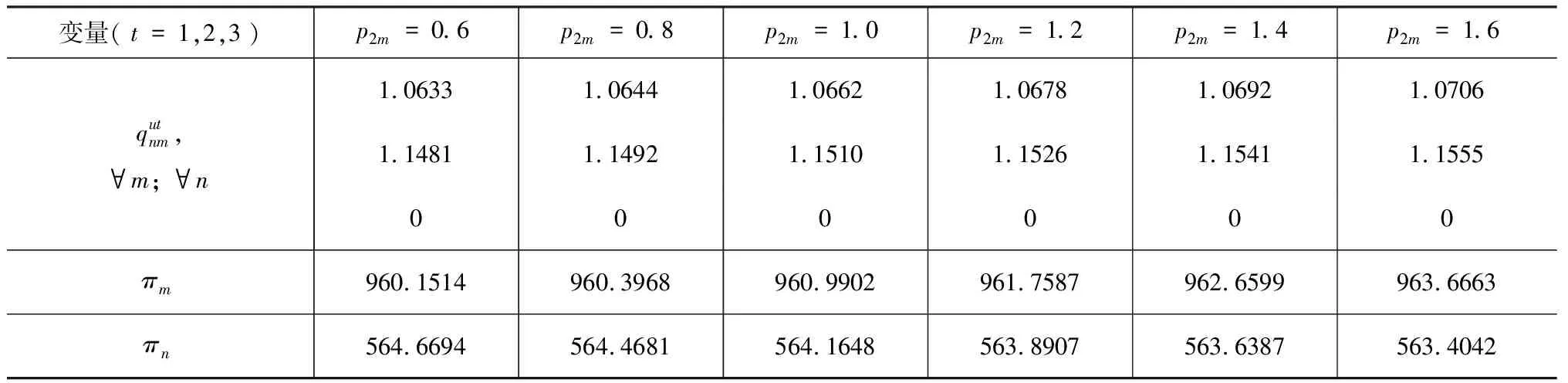
续表1 考虑再制造设计水平的多期闭环供应链网络随p2m变化时的均衡结果

进一步增加至θk>0.45之后，制造商从再制造中获取的收益进一步增加，同时再制造成本增速变缓，所以制造者利润持续增加。零售商不进行产品的生产再制造，其受益于再制造品接受程度θk的提高，利润一直增加。

图3表明当θk<0.3时，市场中仅有新产品，而后出现两种产品共存的情况，新产品的生产量在0.3<θk<0.45区间内减少，然后保持基本稳定；相反，再制造产品的生产量在区间0.3<θk<0.45内增加，然后保持基本稳定；两种产品的总量在θk>0.3后一直增加。

图4则说明：随着再制造品接受程度θk的提高，制造商将在第二期末减少新产品库存并增加再制造产品的库存以备在第三期销售。

观察图5可以发现，在θk=0.3之前，可再制造设计水平均为0；在θk>0.3后，开始迅速增加，并在θk=0.45附近达到最大值，之后又缓慢地降低。且对于θk=0.45，对应的图2中制造商的利润为最低点，对应的图3中该点为新产品产量快速减少至几乎不减少的转折点，同样也是再制造产品从快速增加至几乎不增加的转折点。

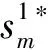
5 结语

本文在多个规划期情景下，考虑了制造商从事再制造时规划期间不同的再制造设计水平设计方案。针对由制造商层、零售商层和需求市场层构成的多期闭环供应链网络，利用变分不等式建立Nash博弈均衡模型。并借助修正投影收缩算法求解。算例中分析了供应链网络均衡状态随p2m变化的结果、消费者对再制造品的评价系数对供应链网络均衡状态的影响、政府规定的强制性可再制造设计水平约束和单个需求市场的再制造品评价系数对企业利润和再制造设计水平的影响。研究发现，p2m的增加使得再制造设计水平增加，并可使得供应链网络的整体状况变好，这就要求企业增大对再制造生产技术的投入，且p2m的增加能促进原材料的充分利用，符合可持续发展战略的要求；政府的强制性再制造水平约束将在一定程度上影响企业的最优决策；消费者对再制造品的评价可使制造商的利润先减小再增加，即当消费者对再制造品的认可程度从较低水平增长至中等水平的过程中，因再制造产品价格提升所带来的利润增加额无法弥补提高可制造性水平所增加投入的成本，这就要求制造商不要因暂时的利润下降就完全否定消费者对再制造品评价增加的作用，待消费者的评价进一步增加后，利润将迎来转机。

由于产品的再制造设计需要把产品生产、销售并回收以后，经较长时间才能在生产过程中反应出成本节约的优势，本文所建模型主要适用于制造商长期进行产品再制造的情形。在企业的实践中，符合本文研究假设情况的企业已经大量存在且还将继续增加。

本文的研究尚存在一些不足， 如本文只考虑了单产品流的情形和回收者是由零售商来承担，未来可拓展至多产品流以及第三方或者制造商来承担回收废旧品的情形。

附录：

变分不等式(25)解存在性和唯一性证明。

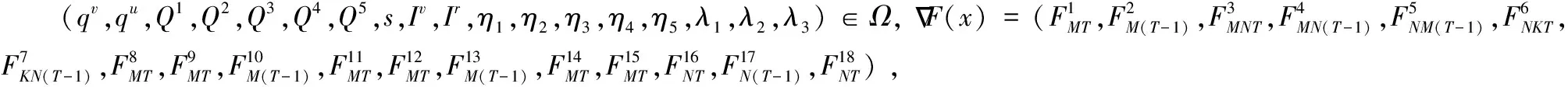
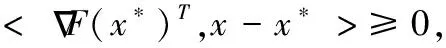
(17)

其中<·,·>表示向量内积。

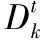
证明：根据决策变量经济学意义，所有变量非负，可再制造设计水平取值不超过1；又市场规模有上界，由式(5)、式(11)和式(12)，制造商的生产量和交易量均有界，则式(16)可行域为紧集。

根据函数可微的假设，式(17)的梯度函数连续，由标准定理，式(17)存在一个解。

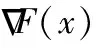
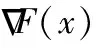
严格单调性证明参考Nagurney[30]。