经验模态分解在切削振动信号分析中的应用

贾广飞 孙师泽 武哲

摘要：为了分析切削振动的变化规律及产生根源，采用在线监测的方法采集振动信号，提出了运用经验模态分解对振动信号进行分析的方法，构建了分段频率变化的仿真振动信号，分别对仿真振动信号进行短时傅里叶变换、小波变换和经验模态分解时频分析。结果表明，经验模态分解方法具有更高的时频分辨率，运用经验模态分解方法对实际振动信号进行分析，提取典型分量绘制希尔伯特幅值谱，能较好地反映振动信号的时频变化规律。经验模态分解适合对切削振动信号进行分析，但是需要对算法的模态混叠及计算效率低等不足进行完善。研究结果对非平稳信号的分析具有参考价值。

关键词：切削加工工艺；切削振动；信号检测；信号分析；经验模态分解

中图分类号：TH16文献标志码：Adoi： 10.7535/hbgykj.2018yx03011

切削振动是指在机床切削加工过程中刀具和工件之间的相对振动。当这种振动达到一定程度时，会影响工件的加工精度和表面质量，甚至在工件表面产生振纹，缩短刀具的使用寿命，并伴随着较大的噪声，这在精加工过程中是不允许的。因此，对切削振动进行机理研究和在线监测是很有必要的。GUILLEM等[1]综述了切削振动并分为3种类型：自由振动、受迫振动和自激振动。文献＼[2＼]总结了切削颤振常用的在线监测方法和对振动信号分析的方法。切削振动信号通常为包含多频率成分和干扰噪声的复杂信号，很难直接从时域分析中分辨出包含哪些简谐振动成分。研究人员对切削振动的分析方法主要有：通过振动信号的时域统计特征分析切削振动，如方差[3-4]、切削力信号的平均偏差比[5]、时序信号的排列熵[6]；通过频域分析方法分析切削振动，第3期贾广飞，等：经验模态分解在切削振动信号分析中的应用河北工业科技第35卷如加速度信号的幅值谱幅值[7]、切削力信号功率谱密度比[8-9]；通过时频分析方法分析切削振动，如去趋势波动分析法[10]、小波分析[11-12]和小波包分解[13]。经验模态分解方法是近年来提出的一种较新的时频分析方法，其基于数据自身的尺度特征进行信号分解，是一种自适应的信号分析方法，在分析非平稳、非线性数据时具有明显的优势。由于切削颤振信号是一种典型的非线性、非平稳信号[14]，因此，本文将经验模态分解方法应用到切削振动信号分析中。

1经验模态分解的基本原理

经验模态分解与建立在先验基函数上的傅里叶分析和小波分析有着本质的区别，无需预先设定任何基函数，是基于信号（数据）自身的尺度特征进行的分解，是一种自适应的信号分析方法。经验模态分解将包含多频率成分的信号，看成由多个简单本征振荡模式组成，每一个简单本征振荡模式称为一个本征模函数，一个本征模函数必须满足2个条件：1）在整个数据段，极值点的个数和过零点的个数必须相等或最多相差一个；2）在任何数据点，由局部极大值点形成的上包络和由局部极小值点形成的下包络的均值为零[15]。实际信号几乎不满足这两个条件，必须进行逐步分解，才能筛选出满足条件的一个个本征模函数。其算法流程见图1，分解步骤如下：

1）找信号x（t）的局部极大值点和极小值点；

2）用三次样条曲线分别连接极大值点、极小值点，形成上包络线和下包络线；

3）由上、下包络线的平均形成均值包络线m1（t）；

4）寻找第1个本征模函数c1（t），计算残余r1（t）=x（t）-c1（t）；

5）将残余r1（t）作为新数据，重复执行步骤1）—步骤4），最终得到n个本征模函数。

因此，通过经验模态分解，将信号分解为n个本征模函数与一个残余分量和的形式，见式（1）。x（t）=∑nj=1cj（t）+rn（t）。（1）

2經验模态分解对仿真振动信号的分析

为了说明经验模态分解在分析多频率成分振动信号的优势，构建一个包含3种频率成分的随时间分段变化的仿真振动信号。其表达式为

x（t）=sin（0.1πt），1≤t≤342；sin（0.4πt），342图2给出了该仿真振动信号的时域波形。从图2可以看出，该仿真信号的时域波形分3段发生频率变化，但是不能显示频率的具体数值。

时频分析可以从时域和频域两个维度展示信号的变化情况，常用的时频分析方法有短时傅里叶变换（STFT）和小波分析。本文用短时傅里叶变换时频谱和小波时频谱展示仿真信号的时频变化，并与经验模态分解后的希尔伯特幅值谱进行对比，如图3—图5所示。

可以看出，短时傅里叶变换谱、小波时频谱和希尔伯特幅值谱均能从时间域和频率域两个维度反映仿真信号的变化。短时傅里叶变换需要预先设定时间片段和固定的窗函数，而且谱图有一定的重叠，适合分段平稳信号，不适合非平稳信号；小波变换在继承短时傅里叶变换局部化思想上，采用随频率可变的时间-频率窗口，相比短时傅里叶变换具有更高的时频分辨率，但是频率分辨率不一致，低频较好，高频较差；经过经验模态分解后的信号的希尔伯特幅值谱，不需预先设定基函数，完全依据信号自身的特性进行分解，相比小波变换具有更高的时频分辨率，而且频率分辨率一致，更加精细。因此，通过对分段仿真振动信号不同时频分析方法的对比，经过经验模态分解后的希尔伯特幅值谱具有更好的时频分辨率，是一种较好的时频分析方法。

3经验模态分解分析实际振动信号

实际切削加工中产生的振动信号与仿真振动信号存在较大的差别，往往包含更多的频率成分，包含较多的干扰和噪声，而且信号有时还具有非平稳特征。为了进一步检验经验模态分解方法在分析实际切削振动信号的有效性，采用加速度传感器采集实际切削振动信号。实际振动信号（原信号）及对其经验模态分解后的前6个分量如图6所示。分别对原信号及前6个分量做快速傅里叶变换，得到对应的幅值谱，如图7所示。

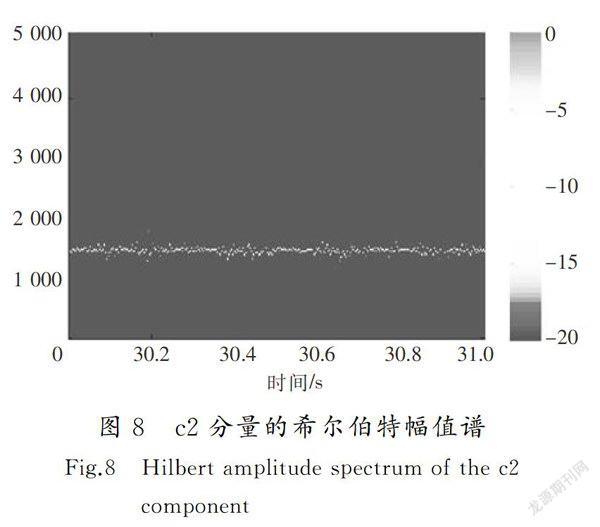
从图6可以看出，原信号经由经验模态分解后被自适应地分解成一系列的本征模函数c1—c6（c6后面的分量由于较弱被省略）；从图7可以看出，原信号的频谱中包含高频噪声以及1 491，997和498 Hz的主要频率成分，c1分量对应高频噪声，c2分量对应1 491 Hz频率成分，c3分量对应997 Hz频率成分，c4分量对应498 Hz频率成分，c5和c6幅值较小可忽略。从c1到c6，频率按照从高到低排列，而且c1与c2，c2与c3之间存在频率混叠，但是混叠的频率成分幅值远小于主要频率成分的幅值，能够从幅值上区分开。选取幅值较大的c2分量进行分析，绘制其希尔伯特幅值谱，如图8所示。

从图8可以看出，c2分量的希尔伯特幅值谱具有较好的时频分辨率，谱线的频率坐标聚焦在1 490 Hz附近且波动较小，从谱线颜色上可以看出频率幅值随时间的变化规律。由此可见，针对实际切削振动信号，经验模态分解方法能够将原始信号中自适应地分解出一个个单一频率成分的信号，选取其中典型的频率分量做进一步的时频分析，去掉了不需要的干扰， 突出了重点，是一种较好的时频分析方法。经验模态分解算法在理论上还存在一些缺陷，如模态混叠、端点效应及计算效率问题，所以c2分量只是近似单一频率成分，还包含着c3分量997 Hz成分的频率混叠和少量的干扰，其希尔伯特幅值谱存在较小的波动，但是混叠的频率成分（997 Hz）幅值远小于主要频率成分（1 491 Hz）的幅值，从幅值上可以区分开，所以在应用中是可行的，对该方法存在的缺陷进行改善后，在实际应用中效果更佳。

4结语

经验模态分析方法从基本原理上决定了其对数据能够进行自适应分解。通过对仿真振动信号的分析可知，经验模态分解相比短时傅里叶变换和小波变换，在对信号时频分析方面具有更大的优势，具有更高的时频分辨率。通过对实际切削振动信号的分析可知，经验模态分解能够将原始信号按频率从高到低分解为一系列相对单一的频率成分，对典型的频率分量做进一步的时频谱分析，可以增强信号分析的针对性，可见对切削振动信号的分析是可行的。但是，经验模态分解算法在理论上还存在一些缺陷需要继续完善，因而对实际切削振动信号的分析效果还有待进一步提高。

参考文献/References：

[1]GUILLEM Q， JOAQUIM C. Chatter in machining processes： A review [J]. International Journal of Machine Tools & Manufacture， 2011， 51： 363-376.

[2]贾广飞. 难加工材料铣削加工中颤振与刀具磨损识别方法研究[D].武汉：华中科技大学，2014.

JIA Guangfei. Research on Chatter and Tool Wear Recognition Methods in the Difficult-to-cut Materials Milling[D]. Wuhan： Huazhong University of Science and Technology， 2014.

[3]RAHMAN M， ZHOU Q， HONG G S. On-line cutting state recognition in turning using a neural network [J]. International Journal Advanced Manufacturing Technology， 1995， 10：87-92.

[4]于英華，徐兴强，徐平.以方差和互相关系数判别切削颤振的仿真研究[J].组合机床与自动化加工技术，2007，5：24-26.

YU Yinghua， XU Xingqiang， XU Ping. Simulation studies on judging of chatter by variance and mutual coefficient[J]. Modular Machine Tool and Automatic Manufacturing Technique， 2007，5：24-26.

[5]SOMKIAT T， TOSHIMICHI M. Intelligent monitoring and identification of cutting states of chips and chatter on CNC turning machine [J]. Journal of Manufacturing Processes， 2008， 10：40-46.

[6] USHA N， BINDU M K， NAMBOOTHIRI V N N， et al. Permutation entropy based real-time chatter detection using audio signal in turning process[J]. International Journal Advanced Manufacturing Technology， 2010， 46：61-68.

[7]康晶，冯长健，杨国田.离散隐马尔可夫模型在颤振预报中的应用研究[J].机械科学与技术，2008，27（3）：360-364.

KANG Jing， FENG Changjian， YANG Guotian. Application of DHMM pattern recognition theory to chatter prediction[J]. Mechanical Science and Technology，2008，27（3）：360-364.

[8] KULJANIC E， SORTINO M， TOTIS G. Multisensor approaches for chatter detection in milling [J].Journal of Sound and Vibration， 2008， 312： 672-693.

[9]KULJANIC E， TOTIS G， SORTINO M. Development of an intelligent multisensor chatter detection system in milling [J]. Mechanical Systems and Signal Processing， 2009， 23：1704-1718.

[10]VELA-MARTINEZ L， JAUREGUI-CORREA J C， RODRIGUEZ E， et al. Using detrended fluctuation analysis to monitor chattering in cutter tool machines[J]. International Journal of Machine Tools and Manufacture， 2010， 50（7）：651-657.

[11]吴石，林连冬，肖飞，等. 基于多类超球支持向量机的铣削颤振预测方法[J].仪器仪表学报，2012，33（11）：2414-2421.

WU Shi， LIN Liandong， XIAO Fei， et al. Milling chatter prediction method based on multiclass hypersphere support vector machine[J]. Chinese Journal of Scientific Instrument， 2012， 33（11）： 2414-2421.

[12]WANG L， LIANG M. Chatter detection based on probability distribution of wavelet modulus maxima [J]. Robotics and Computer-Integrated Manufacturing， 2009， 25： 989-998.

[13]YAO Z H， MEI D Q， CHEN Z C. On-line chatter detection and identification based on wavelet and support vector machine [J]. Journal of Materials Processing Technology， 2010， 210：713-719.

[14]HAMED M， MOHAMMAD R M， GHOLAMREZA V. Dynamics of regenerative chatter and internal resonance in milling process with structural and cutting force nonlinearities [J]. Journal of Sound and Vibration， 2012， 331：3844-3865.

[15]HUANG N E， SHEN Z， LONG S R， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proc R Soc Lond A， 1998，454：903-995.第35卷第3期河北工業科技Vol.35，No.3