AZ31B镁合金板材冷轧成形应力应变响应的数值模拟

任一方 蓝永庭 陈渊 王帅

摘 要：为了研究AZ31B型镁合金板材在室温轧制成形过程中应力应变响应规律，采用Johnson-cook本构关系对AZ31B镁合金板材在不同轧制工艺下的单道次冷轧成形进行数值模拟.分别在压下量为2%、5%、8%，应变速率分别为0.1 s-1、1.0 s-1、10.0 s-1的条件下，开展了不同压下量及不同应变速率组合对轧件应力应变响应的模拟研究.模拟结果表明，在压下量为5%，应变速率为10.0 s-1时，AZ31B镁合金板材变形过程中的局部最高应力为267.100 MPa，低于材料极限应力282.900 MPa.局部最高应变为4.454×10-2，低于宏观断裂应变0.2.相比其他工艺条件，此条件是较为合理的冷轧工艺.

关键词：AZ31B镁合金；冷轧；压下量；应变速率；数值模拟

中图分类号：TG335.5；O344.3 DOI：10.16375/j.cnki.cn45-1395/t.2018.03.007

0 引言

作为一种高性能的轻质合金材料，镁合金因其拥有较高比强度、比刚度，以及铸造、切削加工性能良好等优点，被广泛应用于国防军工、交通运输、航空航天及电子等工业领域[1].镁及镁合金的晶体结构决定了镁合金室温时的塑性变形能力较差的特点[2].但是通过塑性成形的镁合金产品相比传统压铸成形方式拥有更好的力学性能[3]，且产品结构也更具多样化.

轧制作为金属板材塑性成形的一个重要成形工艺，具有工艺简单、效率高等优点.就目前而言，在研究镁合金板的轧制成形工艺中，许多研究主要进行的是考虑温度的热轧研究，而进行冷轧的研究相对较少.文献[4]研究了镁合金板材在常温下的塑性变形行为，认为镁合金冷轧成形应采用多道次，且道次压下量应控制在5%～10%，但并未考虑应变速率的影响.文献[5]对AZ61镁合金铸轧板进行了不同温度下的轧制试验，发现室温轧制时，其极限成形能力为10%，但在轧件边缘处出现了微小的裂纹.CHANGL 等[6]研究结果发现在常温轧制时，单道次极限变形量为22%，但此时已出现了明显裂纹.

由于冷轧不用对温度实施控制，为工业生产中实现节能减排提供了一种途径.本文对AZ31B型镁合金板坯在室温条件下轧制成形中应力应变响应进行数值模拟，通过比较模拟结果，可获得较为合理的冷轧工艺参数.

1 板材轧制有限元模型

轧制模拟时所用的AZ31B型镁合金板坯通过热挤压方式获得，其材料成分如表1所示，参照文献[7]的研究，在退火温度为400 ℃，退火时长10 min热处理工艺条件下，热轧镁合金板坯室温下的极限强度为282.9 MPa.模拟时忽略各向异性的影响.

1.1 几何模型及网格划分

为提高轧制模拟的准确性，建立了三维有限元模型.板坯采用二轧辊轧制，上下轧辊完全相同，图1为板坯和轧辊的几何模型，轧制模型的几何参数见表2.轧件和轧辊模型时均采用C3D8R六面体缩减单元将进行网格划分.考虑到轧辊的刚性远大于轧件，故将轧辊设定为刚性体，在计算时轧辊不发生变形.

1.2 材料本构模型

轧辊材料采用合金钢（材质为9Cr2Mo），板坯材料为AZ31B型镁合金，为提高板材冷轧过程计算的准确性，以及模拟过程的计算精度，需给出AZ31B型镁合金轧制变形时的一些参数.轧辊和轧件材料室温下的具体参数如表3所示.

这里采用Johnson-cook本构模型对板坯轧件的变形进行描述.该模型形式简单、适用于金属大变形.其表达形式如下：

结合AZ31B型镁合金的试验数据[8]，常温下AZ31B镁合金的Johnson-cook本构模型的参数如表4所示，将各个参数代入式（1）即可得室温下AZ31B型镁合金本构方程.

2 轧制工艺参数

2.1 摩擦系数的选择

AZ31镁合金薄板冷轧过程中，当用石墨油来润滑时，轧辊与轧件间摩擦系数为0.069，无润滑时，轧辊与轧板之间干摩擦系数为0.350[9].在进行有限元模拟时，轧件与轧辊之间的接触采用面-面的接触类型，摩擦公式使用罚函数摩擦，这里取接触面摩擦系数为0.250.

2.2 压下量及轧制速度

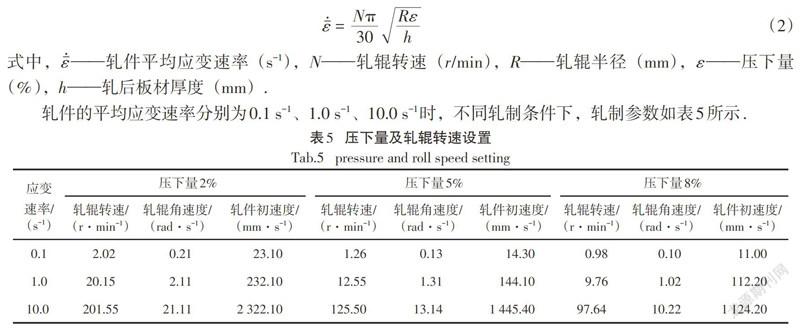
在室温条件下，文中采用不同压下量以及不同应变速率组合来分析轧件的成形过程中应力应变的演变.模拟选取的单道次压下量分别为2%、5%、8%，以及应变速率分别为0.1 s-1、1.0 s-1、10.0 s-1的不同组合进行模拟试验.根据Wusatowski公式可以计算出当轧件的平均应变速率一定时，不同轧制压下率与对应的轧辊转速关系式为：

3 模拟结果分析

有限元模拟的分析步采用ABAQUS/Explicit动力学分析.为了提高计算效率，在保证精度的前提下，引入适当的质量缩放系数，本文缩放系数为50.通过模拟计算可以对材料各物质点在加载过程中的应力应变不均匀响应进行预测.尽管计算应力出现的位置与试验中材料物质点应力的位置不是一一对应，但模拟计算的结果可以反映材料在加载过程中可能出现的最高应力水平.因此这些应力水平与材料极限应力（极限应力是通过单轴加载试验确定的材料强度应力，材料物质点应力大于材料強度应力时材料失效）进行比较，依此可以估计材料在加载过程中出现破坏失效的倾向，可为优化实际的轧制工艺参数提供理论指导.

3.1 压下量为2%，不同速率的应力应变响应

单道次压下量为2%、应变速率分别为0.1 s-1、1.0 s-1、10.0 s-1条件下轧制结束时的轧件应力分布和应变分布，如图2和图3所示.从图2中可以看出，应变速率为0.1 s-1时轧件的应力分布规律与应变速率为1.0 s-1时的相似.轧件应力从中心处到两端先增大后减小，轧件中部、头部及尾部应力值较小；应变速率为10.0 s-1时，轧件前半部分应力较小，后半部分应力较大.从图3所示不同速率下的应变云图中可以看到，轧件的应变主要集中于中部，头部和尾部几乎没有应变，这可能是压下量较小造成的.压下量为2%时，应变速率为0.1 s-1、1.0 s-1、10.0 s-1的条件下，轧件在轧制变形过程中所受的最高应力分别达到237.1 MPa、239.3 MPa、242.9 MPa，均小于AZ31B型镁合金板坯室温下的极限应力282.9 MPa.故压下量为2%时，在3种应变速率的条件下冷轧，板坯不会出现裂纹.

表6给出了压下量2%时，3种应变速率下轧件在轧制完成后的残余应力应变的最大值、最小值和平均值.这些值是衡量板坯成形质量的重要指标，平均应力应变越小，则轧件变形越均匀.从表中可以看出应变速率为10.0 s-1时的残余最大应力和平均应力是3种速率中最高的；而应变速率为0.1 s-1时的残余最大应力值和平均应力值最低.残余应变的最大值和平均值则随着应变速率的增大而增大，在应变速率为0.1 s-1时的残余最大应变值和应变平均值最小.通过不同速率下轧件残余平均应力和平均应变的比较，可以发现应变速率为0.1 s-1时，轧件变形较为均匀.

3.2 压下量为5%，不同速率的应力应变响应

单道次压下量为5%、应变速率分别为0.1 s-1、1.0 s-1、10.0 s-1条件下轧制结束时的轧件应力分布和应变分布如图4和图5所示.通过图4不同速率下应力分布的对比发现，应变速率为0.1 s-1时与应变速率为1.0 s-1时轧件的应力分布较为相似，上表面中间区域应力较小，侧面应力较大.应变速率为10.0 s-1时，轧件表面应力的分布较为一致.从图5可以看出，应变速率为0.1 s-1、1.0 s-1以及10.0 s-1时轧件的应变分布规律相似，轧件头部和尾部应变较小，中部应变较大.压下量为5%时，应变速率为0.1 s-1、1.0 s-1、10.0 s-1的条件下，轧件在轧制变形过程中所受的最高應力分别达到268.2 MPa、267.1 MPa、277.0 MPa，均小于轧件材料室温下的极限应力282.9 MPa，故实际轧制过程中轧件不会开裂.

压下量5%时，在轧制完成后的残余应力应变的最大值、最小值和平均值如表7所示，其中轧件在应变速率为0.1 s-1时的残余最大应力值最高；应变速率为1.0 s-1时的平均应力值最高；应变速率为10.0 s-1时的残余最大应力值和平均应力值最低.在应变速率为1.0 s-1时的残余最大应变值最小，应变速率为10.0 s-1时的残余最大应变值最高；平均值则随着应变速率的增大而增大，但3种速率下的平均应变相差并不大，因此，当压下量为5%时，在应变速率为10.0 s-1的条件下，轧件成形质量较好.

3.3 压下量为8%，不同速率的应力应变响应

单道次压下量为8%，应变速率分别为0.1 s-1、1.0 s-1、10.0 s-1条件下轧制结束时的轧件应力分布和应变分布如图6和图7所示.从图6中可以看出，轧件在3种应变速率下的应力分布规律类似，轧件表面中间区域及头部的应力较小，尾部应力较大.通过图7中应变分布云图的对比，可以发现在3种应变速率下的应变分布也较为相似，头部应变较小，中间应变较大.压下量为8%时，应变速率为0.1 s-1、1.0 s-1、10.0 s-1的条件下，轧件在轧制变形过程中所受的最高应力分别达到291.4 MPa、289.6 MPa、292.0 MPa，均稍高于材料室温下的极限应力282.9 MPa，说明在压下量为8%工艺条件下，实际轧制中板坯可能会产生裂纹.

压下量8%时，在轧制完成后的残余应力应变的最大值、最小值和平均值如表8所示，轧件在应变速率为1.0 s-1时的残余最大应力值最高，10.0 s-1时的残余最大应力值最低；残余平均应力随着应变速率的增加而增加，10.0 s-1时的最大，0.1 s-1时的最小.残余应变的最大值和平均值也随着应变速率的增大而增大，在应变速率为0.1 s-1时应变均值最小.

4 模拟结果验证

文献[10]针对热挤压态AZ31镁合金进行了压下量分别为7%、10%、15%、19%的室温轧制实验，其结果表明当压下量为7%时，其显微组织中有少量的剪切带与孪晶出现；当压下量增大到10%时，出现大量的剪切带与孪晶；压下量为19%时的剪切带与孪晶最多.当压下量大于10%时，板材出现边裂，甚至中心开裂.

将本文数值模拟结果与文献[10]的实验结果从压下量方面进行对比.模拟压下量为8%时，轧件在变形时所受到的最大应力值略大于材料的强度极限，可能会使材料内部萌生出微小裂纹；对比文献[10]中压下量由7%增大到10%时材料微观组织出现大量剪切带与孪晶的情况，在裂纹产生的可能倾向上实验结果与模拟分析基本吻合.

5 结论

采用压下量为2%、5%、8%，应变速率分别为0.1 s-1、1.0 s-1、10.0 s-1的工艺条件，研究了不同压下量与应变速率的组合对AZ31B型镁合金轧件的应力应变分布的影响，主要结论有：

1）压下量为2%时，由于变形量较小，轧件在不同应变速率下变形过程中的最大应力值均小于AZ31镁合金的极限强度.在应变速率为0.1 s-1时，试件变形较为均匀，因此镁合金冷轧成形过程时，在压下量较小的情况下，可采用低应变速率来获得较好的成形质量，但采用较小的压下量进行轧制时会增加轧制道次.

2）在压下量为8%的条件下，轧件在0.1 s-1、1.0 s-1、10.0 s-1速率下变形过程中的最大应力分别为291.4 MPa、289.6 MPa、292.0 MPa，均大于材料的极限强度282.9 MPa，说明实际轧制过程中，8%的压下量会造成轧件开裂.

3）综合应力应变的情况看，当AZ31B型镁合金冷轧道次压下量为5%时，与应变速率为0.1 s-1、1.0 s-1时的相比，应变速率为10.0 s-1时轧件的最大应力值和平均应力值最小，分别为186.3 MPa和81.6 MPa.成形过程中的最大应力为277.0 MPa，小于材料的极限强度282.9 MPa.因此在道次压下量为5%，应变速率为10.0 s-1时的条件下，与0.1 s-1、1.0 s-1的速率相比轧件成形质量较好，且轧制效率也较高；与道次压下量为2%的条件相比，可以减少轧制道次，该条件是较为合理的冷轧工艺.

参考文献

[1]李苗苗，武宝林，张利，等. AZ31镁合金板材多道次轧制压下量对变形能力的影响[J].热加工工艺，2017（3）：38-41.

[2]卢立伟，赵俊刘，龙飞，等.镁合金大塑性变形的研究进展[J].材料热处理学报，2014，35（S1）：1-7.

[3]宋鹏飞，王敬丰，潘复生. 高强变形镁合金的研究现状及展望[J].兵器材料科学与工程，2010，33（4）：85-90.

[4]刘长瑞，王伯健，王庆娟. 镁合金常温下的塑性变形行为[J].轻合金加工技术，2005，33（3）：43-46.

[5]李英虹，宋波，郭箐等. 不同温度下AZ61镁合金铸轧板轧制极限变形量的研究[J].热加工工艺，2015（23）：130-132.

[6]CHANG L，SHANG E F，WANG Y N，et al.Texture and microstructure evolution in cold rolled AZ31 magnesium alloy[J].Mater. Charact，2009，60（6）：487-491.

[7]詹美燕，李元元，陈维平，等.AZ31镁合金轧制板材在退火处理中的组织性能演[J].金属热处理，2007，2（7）：8-12.

[8]ULACIA I，SALISBURY C P，HUETADP I，et al. Tensile characterization and constitutive modeling of AZ31B magnesium alloy sheet over wide range of strain rates and temperature[J].Journal of Materials Processing Technology，2011，211（5）：830- 839.

[9]王露萌.AZ31镁合金板材轧制工艺的数值模拟研究[D].哈尔滨：哈尔滨工业大学，2008.

[10]肖睿.AZ31退火工艺对冷轧AZ31镁合金板材组织和织构的影响[D].重庆：重庆大学，2012.