基于ABAQUS的钢筋混凝土悬臂梁挠度分析

李荣荣 朱双凯

摘 要：传统混凝土挠度计算是先通过试验方法测量混凝土弹性模量，再通过弹性模量求解挠度。在试验求解弹性模量过程中，存在费力和难以全面检测等缺点。本文采用ABAQUS建立钢筋混凝土悬臂梁模型，在不同载荷的作用下产生弯曲变形，通过多组数值计算，建立压力和挠度之间的关系方程。本研究可对相关工程提供指导。

关键词：ABAQUS；混凝土；数值分析；挠度

中图分类号：U414 文献标识码：A 文章编号：1003-5168（2018）07-0111-03

Finite Element Analysis of Reinforced Concrete Cantilever Based ABAQUS

LI Rongrong ZHU Shuangkai

（Henan University of Urban Construction，Pingdingshan Henan 467036）

Abstract： The deflection calculation of traditional concrete is to measure the elastic modulus of concrete by testing method first， and then to calculate the deflection by elastic modulus. In the process of testing elastic modulus， the method has many shortcomings， such as laborious and difficult to detect comprehensively. In this paper， a model of reinforced concrete cantilever beam was established by ABAQUS. The bending deformation was produced under different loads. The equation of the relationship between pressure and deflection was established by many groups of numerical calculations. This study can provide guidance for related projects.

Keywords： ABAQUS；concrete；numerical analysis；deflection

钢筋混凝土材料是一种力学性能非常复杂的建筑材料。迄今为止，钢筋混凝土的本构模型还不能被任意一种理论所描述[1]。工程设计过程中，弹性模量往往是钢筋混凝土悬臂梁设计的关键，其在梁的变形、裂缝扩展等方面是必不可少的指标[2]。在弹性模量已知的情况下，采用共轭梁法可轻松求解挠度。但对于配筋不同的混凝土悬臂梁，不能及时测量给出弹性模量。基于此，计算混凝土悬臂梁的挠度显得更为重要。ABAQUS在模拟混凝土材料的非线性关系是行之有效的[3]。

1 受弯构件挠曲变形的影响因素分析

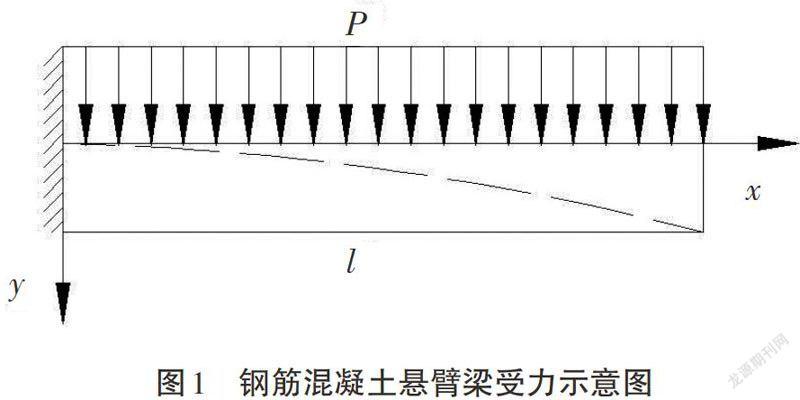
图1为钢筋混凝土悬臂梁受均布荷载的模型，其中，抗弯刚度为EI，全梁受均布面荷载作用，集度为P，根据材料力学相关理论，建立载荷与挠度之间的关系。

在工程中，常用的受弯构件的挠度远小于跨长，梁轴线受力弯曲成一条平坦的曲线。由于横截面沿x轴方向的线位移非常小，对比挠度可以忽略不计。故设定好坐标系，梁变形后的横坐标与轴线挠度的关系为：

[ω=fx] （1）

式中：[ω]为该点的挠度；x为混凝土悬臂梁变形前轴线上任意一点的横坐标。悬臂梁变形后的轴线为挠曲线，其表达式则称为挠曲线方程。为求得梁的挠曲线方程，建立曲率k与弯矩M间的物理关系[4]：

[kx=1ρx=MxEI] （2）

平面曲线的曲率可表达为：

[1ρ（x）=±ω1+ω232] （3）

将式（2）代入（1）中，由于M与[ω]的正负相反，可以得到：

[ω1+ω232=-MxEI] （4）

[ω2]与1相比十分微小，故[1+ω2]≈1，式（4）近似表述为：

[ω=-MxEI] （5）

由于梁的弯曲刚度[EI]为一常量，改写上式为：

[EIω=-Mx] （6）

积分后可得：

[EIω=-Mxdxdx+c1x+c2] （7）

由面载荷集度P求线载荷集度p为：

[p=Pb] （8）

根据以上理论分析及计算可以得到：

[ω=px224EIx2+6l2-4lx] （9）

当l=x时挠度最大，即

[ωb=Pl48EIb] （10）

式中：E为梁的弹性模量；I为梁截面的惯性矩，[I=bh312]，b为梁横截面的宽。

2 ABAQUS数值分析校准

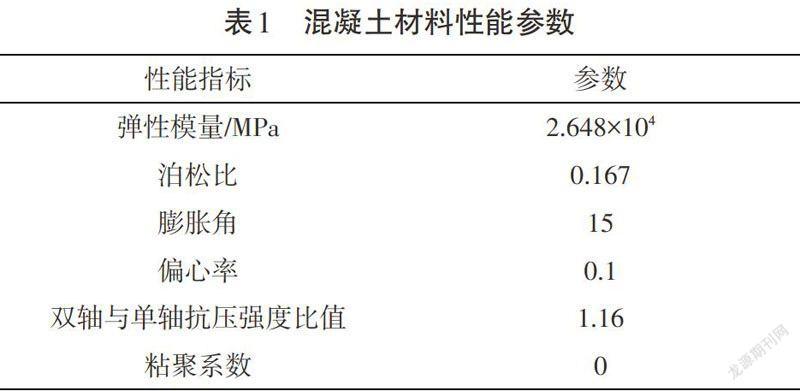
混凝土材料性能如表1所示。该悬臂梁的具体受力情况如图2所示。梁截面尺寸为300mm×400mm，梁长3 000mm，如图3所示。

当悬臂梁为素混凝土，压力为0.03MPa时，图4为采用ABAQUS有限元数值模拟进行计算分析所得到的悬臂梁弯曲变形结果。

由图4变形结果可知，悬臂梁[ωb]=0.77mm，将表1中E代入公式（10）得[ωb]=0.72mm。

数值模拟计算得到的挠度值与实际理论计算挠度值相比稍微偏大，误差仅为6.5%，且计算偏于安全，误差在实际工程应用允许范围之内。数值校核结果表明，利用ABAQUS数值模拟方法来计算钢筋混凝土悬臂梁挠度是可行的。

3 数值计算分析

采用C3D8R单元对混凝土进行建模，同时对钢筋采用T3D2单元进行建模，建模完成后采用Embedded技术对其进行自由度耦合。再使用数值模拟分析，最终得到不同荷载作用下钢筋混凝土悬臂梁挠度值（如表2所示）。图5为梁受压力为0.03MPa时y方向的位移云图，挠度[ωb]=0.037 9mm。图6为不同压力作用下梁的挠度-压力关系曲线。挠度[ωb]与压力P的关系方程为：[ωb]=1.261 9P。

4 结语

通过本文的分析，可得出以下结论。

①基于ABAQUS建模，采用C3D8R单元对混凝土进行建模，同时采用T3D2单元对钢筋进行建模，可以较好地实现悬臂梁的数值模拟计算。

②基于ABAQUS数值模拟计算，得出的素混凝土悬臂梁挠度结果与实际挠度值比较发现，计算结果稍稍偏大，但误差只有6.5%，在误差允许范围之内。这表明ABAQUS数值模拟方法求混凝土悬臂梁挠度的方法是可行的。

③在弹性模量未知的情况下，提出利用ABAQUS软件数值模拟得出钢筋混凝土悬臂梁载荷和挠度关系方程的方法。

参考文献：

[1]吕西林，金国芳，吴晓涵.钢筋混凝土结构非线性理论与应用[M].上海：同济大学出版社，1997.

[2]劉庆涛.钢筋混凝土悬臂梁复合弹性模量研究[J].太原理工大学学报，2012（6）：693-696.

[3]刘劲松.ABAQUS钢筋混凝土有限元分析[J].装备制造技术，2009（6）：69-70.

[4]孙训方.材料力学[M].北京：高等教育出版社，2001.