初中生计算思维能力的现状调查及对策研究

张菊芳?王海燕

摘 要：随着2017版《普通高中信息技术课程标准》的制定和颁布，计算思维的培养越来越受到学校教育的关注。为了探讨如何加强初中与高中学生计算思维能力培养的衔接工作，本文以八年级学生为研究对象，从计算思维的内涵出发，以计算思维的概念框架为线索，设计了与计算思维五要素——算法、分解、抽象、评估和概括相关的问卷，通过问卷调查分析学生的计算思维能力，并以此提出相应的对策建议，旨在为学生计算思维的培养提供参考借鉴。

关键词：信息技术;计算思维;现状调查;对策研究

中图分类号：G434文献标志码：A文章编号：2096-0069（2018）06-0046-05

一、设计与调查

计算思维由麻省理工学院的西蒙·派珀特（Seymour Papert）教授于1996年最早提出[1]，最受关注的代表人物是美国卡内基梅隆大学的周以真教授（Jeannette M.

Wing）。2006年，周以真教授在美国计算机权威杂志上公开定义了计算思维的概念。她认为，计算思维是运用计算机科学的基础概念进行问题求解、系统设计，以及人类行为理解等涵盖计算机科学之广度的一系列思维活动[2]。

2013年，英国南安普敦大学的辛西娅·塞尔比

（Cynthia Selby）博士和约翰·伍拉德（John Woollard）博士根据一项调查发展了计算思维的定义。他们认为计算思维是一种活动，是一个认知或思考的过程，是一种以产品为导向又不局限于解决问题的过程，并借助一个表格总结了12个有关计算思维定义的核心要素，通过排除某些因素缩小了定义的范围，最终得出计算思维包含5个方面，即算法思维（Algorithmic Thinking）的能力、分解（Decomposition）角度思考的能力、抽象（Abstraction）思维的能力、在评估（Evaluation）方面思考的能力以及概括（Generalisation）思维能力。这个定义将解决问题的算法、分解、抽象、評估、概括的思想过程密切联系在一起[3]。

本文试图基于笔者所在实习学校使用的西安交大版八年级下册的信息技术教材，借助计算思维的概念框架和教材第二章——认识计算机程序的教学内容来设计教学的前测问卷，以期了解初中生计算思维能力的现状。在数据调查和统计过程中，先选2个班进行问卷的信度和效度检验，删除未达标题项，最后得出克隆巴赫系数（Cronbachs α）为0.779，大于0.7，KMO值（用于判断是否有效度）为0.769，在0.7到0.8之间，意味着问卷的信效度可行，因此可以对正式问卷做进一步的统计分析。以另外8个班共448名学生作为研究对象发放问卷，借助Excel和SPSS 22.0，针对400份有效问卷对学生的计算思维能力进行分析。

本研究中问卷所起到的作用，一方面是调查八年级学生的计算思维能力，另一方面是作为本章学习内容的引导性材料。问卷除对学生的性别和年级基本情况进行调查外，还包括学生对计算思维的认识和态度倾向及与计算思维五要素相关的测试题目。

调查具体项目紧紧围绕计算思维五要素——算法、分解、抽象、评估和概括展开。其中，“算法”主要了解学生学习解决问题的具体步骤和方法的能力;“分解”主要了解学生将问题分成若干个子问题，使复杂问题得以模块化解决的能力;“抽象”主要了解学生明确问题要求后分析问题，然后再把问题抽象成数据结构和数学模型的能力;“评估”主要是了解学生对自己提出的解决方案不断论证和判断的能力;“概括”主要了解学生把抽象出来的事物的本质属性相联系，运用迁移获得新知识的能力。

二、调查结果分析

（一）学生对计算思维的基本认识

经调查得知，学生对计算思维大多比较陌生，其中知道这个概念的学生才占17.65%。认为计算思维非常重要的学生占35.51%，可见大多数学生并未意识到计算思维的重要性。在接受计算思维相关训练方面，专门针对学生计算思维的相关训练较少，接近一半的学生表示从来没有接受过相关训练，而认为经常或者总是接受训练的学生只有13.5%左右。针对以上分析，可以得出学生对计算思维的重要性认识不足，相关培养工作更是非常欠缺。

（二）学生在计算思维方面的能力现状

这部分主要以问卷典型的题目为例，借助图表和数据对学生思维方面的能力进行具体分析（题目考察角度原因，在此就把算法思维放后面和评估思维一起论述）。

1.分解思维

“你用什么方法计算1-2+3-4+…+99-100的结果？”这道题需要用分解思维，调查得知，两两相减再求和是最快的解决方案，有239名学生选择正确，占到总人数的59.8%，即一半左右的学生答对，整体分解思维能力一般，并且这种思维能力大多从数学学习中获得，在程序设计中还须通过应用实现迁移才可以达到培养的目的。

2.抽象思维

“求数列1、1、2、3、5、8、13、21、X、55中X的值”这道题目考查学生抽象思维能力。经分析不难发现，这个数列的规律是第3个数等于前2个数的和，将其公式化为Fn=Fn-1+Fn-2（n>2），所以X的值为13+21=34。调查可知，49.8%的学生可以找出数列的规律，即几乎有一半的学生答对，抽象思维能力一般。

3.算法和评估思维

问卷题目：有一商品价格在40元以内，采取什么策略能在较短的时间内猜出正确的价格？（假设商品价格为15元）

在数学领域中，二分法是针对区间[a，b]上连续不断且f（a）·f（b）<0的函数y=f（x），通过不断地把函数f（x）的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法。同理，在编程语言中二分法的基本理念是假设数据是升序排列的，在寻找给定值x时，从序列的中间位置开始比较，如果中间值等于x，则查找成功;若x小于中间值，则在数列的前半段的中间位置继续查找;若x大于中间值则在数列的后半段中继续查找，直到找到为止。在设计算法时，针对较大的数据量则适宜采用该方法。采用二分法查找时，数据需是排好序的。上述这个问题应用了二分法的理念，解决这个问题的过程既体现算法思维，又体现评估思维，设计算法就是要提出具体的操作步骤;评估思维主要用于反思和判断自己的算法是否合理和最佳，猜一个指定范围的商品价格通常是可以按步骤完成的。

商品价格是15元，猜在40元之内的商品价格的具体步骤主要分为三步：第一步，商品价格是20元（用二分法找指定范围的中间值，即0—40的中间值），主持人说太高;第二步，商品价格是10元（0—20的中间值），主持人说太低;第三步，商品价格是15元（10—20的中间值），主持人说猜对了。

调查可知有44%的学生得出正确的方案，可见不到一半的学生对二分法基本了解，能够设计出对应的算法，并且个人能够对这个过程进行评估。

4.概括思维

因为二分法是数学领域的术语，大多数学生已经有了这方面的基础，此处只是检验学生的迁移能力，所以此处主要是检验学生是否会用二分法解决问题。

问卷题目：有24个小球，其中有一个质量比其他的轻，利用天平测量至少通过多少次能找到这个小球？

调查得知，有68%的学生找出了方案，即这些学生能将以前所学的二分法的技巧应用于解决这个问题，当然也不排除学生靠经验和直觉解决问题，即使他们并不知道什么是二分法。所以得出结论，一半以上的学生表现出了概括思维能力。

由上所述，从整体来看，学生对计算思维的认识不足，接受的训练不够，对计算思维五要素的理解远远未达到课标的要求，因此需在后续的教学及研究中继续探索。

三、建议对策

（一）教师要重视计算思维的培养，在教学中积极挖掘有关计算思维的内容

教师需要在教学过程中积极挖掘培养学生计算思维的内容，并用生活实例来展现这些内容，让学生理解计算思维，更好地在问题应用中培养计算思维。

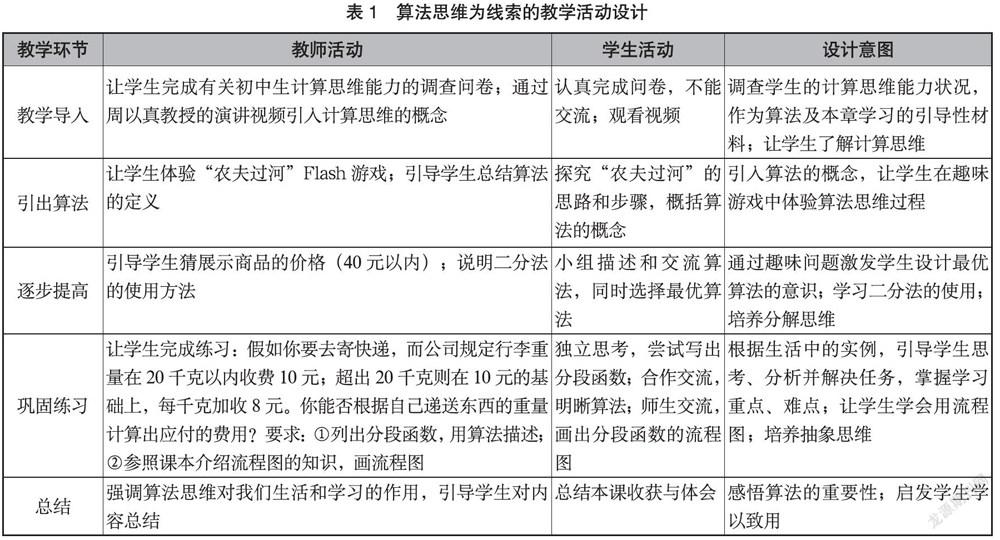
第一，以计算思维五要素为框架实现教学内容的模块化。如在“认识计算机程序”这一章中，教材内容主要包括算法、流程图设计及VB（一门计算机语言）的三种基本结构，所有的知识点都可以归类到计算思维五要素之下，因此教师可用计算思维理念组织教学设计，将教学内容按模块或环节归类到五要素之中，其中每个要素可包含若干类活动，如表1所示算法思维为线索的教学活动设计。

第二，针对知识点，提炼计算思维的各要素。如“S=1-2+3-4+…+99-100，求S的值”这道题体现的计算思维要素主要有：①分解转换公式——分解思维;②设计算法——算法思维;③判断算法是否最优——评估思维;等等。

教师要勤于探索研究，选择恰当的方法培养学生的计算思维，本着将课堂还给学生的理念，在讲授知识点的同时要让学生自己探究学习，利用小组合作和自身努力获取实际生活所需的知识技能，如利用项目式学习开展课堂活动就体现了这样的理念。有关项目式学习的定义较多，本文引用美国巴克教育研究所的观点，即项目式学习是一套系统的教学方法，通过对复杂或真实问题进行探究、精心设计项目作品、规划和实施项目任务，让学生掌握所需的知识和技能的过程[4]。项目式学习主要包括提出符合学生兴趣的问題、针对问题制订解决方案、形成与方案相对应的作品和对整个过程进行交流评估四个环节，以项目式学习法培养计算思维，将更有利于提高学生的综合能力。

为了培养学生的计算思维，以“认识计算机程序”为例开展项目，本章主要有6节教学内容，教学计划分为7个课时，设计用4个课时来完成项目的前期准备，目的是为学生开展项目提供知识和工具，普及计算思维的基本知识，主要分为三部分：

首先，基于项目的学前培训，引导学生完成有关计算思维的前测问卷（0.5课时）。

其次，初识VB及编程（成果实现的工具）（1.5课时）。

再次，选择算法中的典型案例（至少包含计算思维的两大要素），引导学生探索。其中，案例1（1课时）：S=1-2+3-4+…+99-100，求S的值。知识点包括转换式子（分解思维）、算法及流程图设计（算法思维）、程序编码（多种思维解决问题）。案例2（1课时）：同表1活动设计中寄快递的案例。知识点：列分段函数（抽象思维）、算法及流程图设计（算法思维）、程序编码（多种思维解决问题）。

要求：设计恰当算法，通过流程图描述，能将算法转换成程序语言并且通过VB设计出作品。项目的具体实施过程按照确定问题、制订方案、形成作品、交流评估四个步骤来进行。

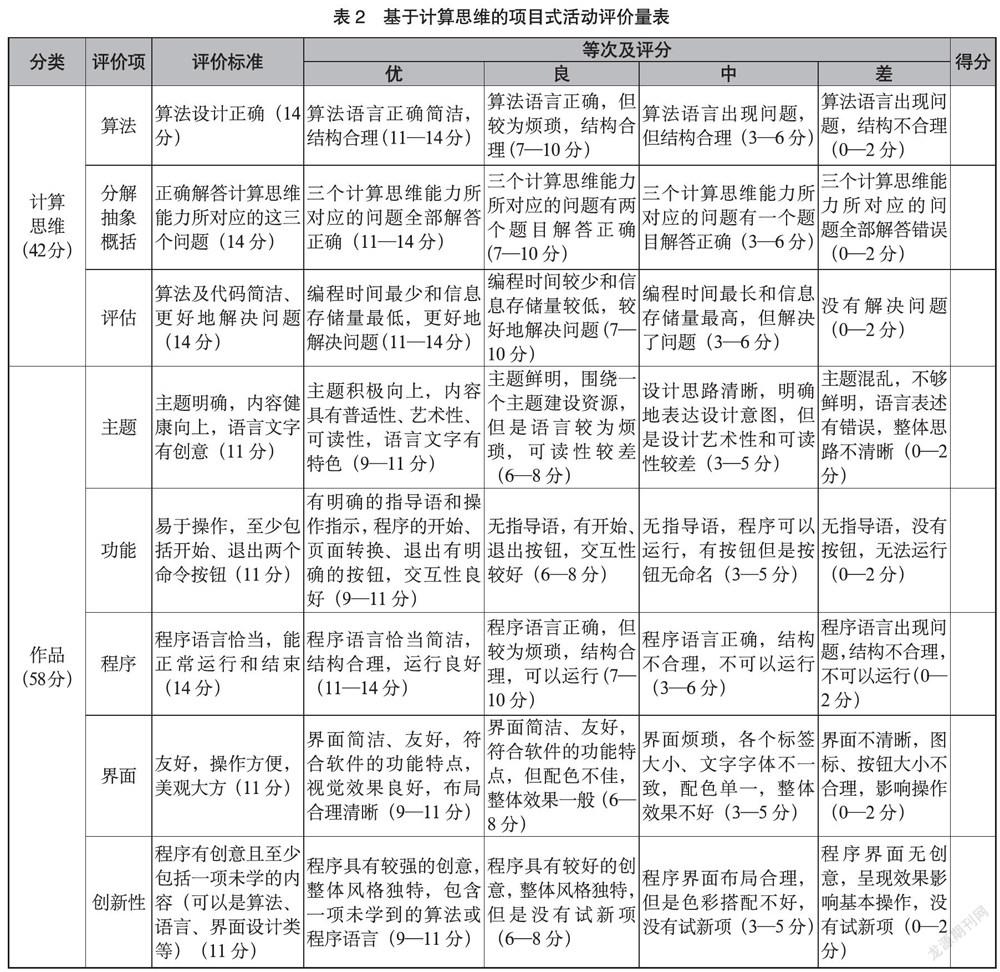
（二）选择可测量的评价方式有效地评价计算思维

计算思维的评价不仅会对学生的学习效果进行反馈，同时会指导教师改进教学中出现的问题，因此评价是非常重要的。如针对上面提到的项目式教学案例，通过项目作品综合评价、计算思维和算法等相关知识点测试来评价学生计算思维方面的学习成效，具体测量方法如表2所示[5]。

当然，有关计算思维的评价方式多种多样，单凭一种测量方式对计算思维能力进行评价是有偏差的，因此针对不同的教学情境可以选择不同的评价方式，如通过前后测问卷、反馈性访谈以及学生课堂交互观察等进行全程评价;设置模拟现实的游戏化情境，通过查看问题的完成情况、分析源代码或者操作心理等也可以对学生的计算思维能力进行评价[6]。

四、结语

计算思维的培养作为当前教育教学关注的焦点，人们不再仅仅关注大学或者高中阶段这种思维的培养，对中小学或者幼儿园的思维启发更加关注，所以在教学中对计算思维的培养要循序渐进，注意学生的水平和接受能力。针对思维意识较强的高年级学生要有意识地提供一些高难度的问题，来培养他们的思维品质;对于低年级的学生可以以问题解决和启发为主，激发学生的主动性。通过实施灵活的教学手段，从而让各个年龄阶段的学生学会这种思维方式，以培养他们灵活解决各种问题的能力。

参考文献

[1]PAPERT S.An Exploration in the Space of Mathematics Edu-cations[J].International Journal of Computers for Mathematical Learning（S1382-3892），1996，1（1）：95-123.

[2]WING J M.Computational Thinking[J].Communication of the ACM（S0001-0782），2006，49（3）：33-35.

[3]SELBY C，WOOLLARD  J.Computational Thinking：the Developing Definition[C].Special Interest Group on Computer Science Education，Atlanta，2013.

[4]巴克教育研究所.項目学习教师指南：21世纪的中学教学法（第2版）[M].任伟，译.北京：教育科学出版社，2008.

[5]教育部.普通高中信息技术课程标准[M].北京：人民教育出版社，2017.

[6]陈鹏，黄荣怀，梁跃，等.如何培养计算思维：基于2006—2016年研究文献及最新国际会议论文[J].现代远程教育研究，2018，（1）：98-112.

Investigation on the Status Quo of Junior Middle School Students Computational Thinking Ability and Countermeasures

ZHANG Jufang，WANG Haiyan

（School of Education，Shaanxi Normal University，Xian，Shaanxi，China 710062）

Abstract： With the formulation and promulgation of the 2017 edition of Standards for Information Technology Courses in Ordinary High Schools，the cultivation of computational thinking has received more and more attention from school education.In order to explore how to strengthen the connection work between the computational thinking ability of junior high school and high school students，this study takes the eighth grade students as the research subjects，and starts from the connotation of computational thinking，and uses the conceptual framework of computational thinking as a clue to design a questionnaire which is related to the five elements of computational thinking：algorithm，

decomposition，abstraction，evaluation and generalization.It analyzes students computational thinking ability through the questionnaire survey.Based on this status quo survey，we propose some corresponding countermeasures，aiming to provide references for the cultivation of students computational thinking.

Key words： information technology;computational thinking;status quo survey;countermeasure research