基于GARCH模型的我国股票价格波动性研究
2018-09-10李亚楠
李亚楠
摘 要:本文利用2012年1月24日至2018年3月21日期间上证综合指数日收盘价的数据,对其收益率序列进行了统计描述,并对上证综合指数的对数价格建立GARCH模型,进行实证分析,得出上证指数的对数价格具有波动率聚集现象的结论。
关键词:GARCH模型 上证指数 波动率
中图分类号:F830 文献标识码:A 文章编号:2096-0298(2018)05(c)-177-02
我国股票市场经历了将近30年的演变,从无到有,从不规范到逐渐规范,可以说我国股票市场未来的发展前景是值得期待的。但是,在看到我国股票市场繁荣的一面的同时,也应该注意到它所蕴含的风险,正是由于这种风险的存在,才使我们开始关注股票价格的波动率。如今对股票价格波动率的研究已经越来越多,它的估计值是否准确直接关系到投资策略的正确与否。
在国外,人们对波动率研究的历史更加悠久。1982年Engle提出了自回归条件异方差(ARCH)模型,它反映了波动率的聚集現象;1986年Bollerslev在前者的基础上提出了广义ARCH(GARCH)模型,对原有的ARCH模型进行了改进,相比ARCH模型而言,GARCH用很少的参数就可以充分描述股票价格的波动率过程;1991年Nelson又进一步提出了指数GARCH模型,它弥补了前面两者的缺陷,使得波动率对股票价格的大幅上升和下降具有不同的反映,即描述了波动率的杠杆效应。
本文主要在GARCH模型的基础上对上证综合指数进行描述,旨在研究近年来我国股票市场的不确定性,并对此进行探讨。最后,本文会对全文内容进行总结并得出相应的结论。
1 模型简介 1.1 ARCH模型简介

GARCH模型相比ARCH模型具有如下的优点:(1)GARCH模型具有降阶的功能,它降低了ARCH模型的阶数,提高了模型整体的准确性;(2)GARCH模型比ARCH模型多了随时间进行演变的特征;(3)GARCH模型比ARCH模型更具有“波动率聚集”现象;(4) GARCH模型比ARCH模型多了延迟项来描述波动率的演变。
2 数据来源
本文考虑到2007年次贷危机发生后经济的恢复期需要3~5年,故选用2012年1月24日至2018年3月21日的上证综合指数日收盘价作为本次研究的指标,用Pt表示,共计1607个数据,数据来源于大智慧数据信息平台。本文试图通过对上证综合指数建立模型来对其波动率进行分析,旨在反应近年来我国股票市场的波动情况。
3 基于GARCH模型的上证指数波动率的实证分析
3.1 上证指数日收益率的基本分析
本文采用连续复合收益率来对上证指数的收益率进行定义,其中第t天的上证指数日收盘价记为Pt,上证指数的日收益率记为rt,则有rt=lnPt-lnPt-1。
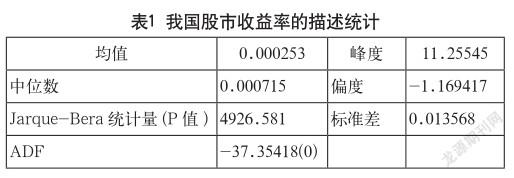
从表1中可以发现所选样本序列的中位数大于其均值,说明其右偏;峰度K=11.25545,说明收益率分布相比于正态分布更具有“尖峰”,这与大量的实证结论保持一致。另外,Jarque-Bera检验统计量的值也说明了上证指数的日收益率序列不服从正态分布。ADF检验统计量表明在即使1%的显著水平下,此收益率序列都是平稳的。
3.2 模型建立
假设我国的股票市场是弱式有效市场,即投资者无法使用当前或者历史的价格对股票的价格作出预测。本文中股票价格的对数序列采用随机游走模型来描述,其形式为:LnPt=βLnPt-1+at,其中εt为随机误差项。
利用Eviews7.2建立随机游走模型得到方程:Ln Pt= 1.000030LnPt-1,从中可以发现LnPt-1的系数接近于1,所以LnPt-1服从随机游走过程。

从图1中可以看出,残差序列具有波动率聚集现象,说明残差序列可能具有异方差性。对at进行ARCH效应的检验得F检验统计量的值为111.6972,P值为0.0000,具体如表2所示。并且残差平方序列的ACF显著不为0,Q统计量在各阶的相伴概率(P值)为0.000,故{a2t}具有自相关性,继而认为残差序列之间不独立。所以可以拒绝残差序列具有同方差的假定,认为时间序列{at}具有异方差性,适合建立波动率方程,即LnPt具有ARCH效应。综上所诉,有理由认为GARCH模型来描述上证指数的波动率是合理的。

3.3 模型检验
3.3.1 方差方程系数检验
从上面的结果可知:a0=6.42×10-7>0,a1=0.066882≥0,β1=0.931943≥0,a1+β1=0.998825<1,故方程参数满足约束条件,认为{at}服从GARCH(1,1)模型。
3.3.2 模型标准化残差检验
对上述GARCH(1,1)模型而言,其标准化残差为:εt=at/σt。利用Eviews7.2检验时间序列{εt}的Ljung-Box统计量为Q(12)=17.466(P值=0.133),Q(24)=26.389(P值=0.334),时间序列{εt2}的Ljing-Box统计量为Q(12)=15.897(P值=0.196),Q(24)=22.949(P值=0.523),因此可以认为GARCH(1,1)模型能充分拟合上证指数对数价格序列与波动率序列的线性相依性,故这样拟合的GARCH(1,1)模型是充分的。

4 结语
本文首先对上证综合指数的收益率序列进行了统计描述,得出上证综合指数收益率序列平稳,且该收益率序列具有尖峰厚尾性的结论。接着对上证指数的对数价格序列建立了随机游走模型,并对其残差序列进行了ARCH效应分析,之后在随机游走模型的基础上建立了GARCH模型,且结果表明该模型拟合度良好。最后,本文对建立的模型进行检验,得出对上证指数对数价格序列建立GARCH(1,1)模型是合适的结论。
现将本文的结论总结如下:(1)我国股票的收益率序列具有尖峰厚尾性;(2)我国股票市场目前属于弱式有效市场,股票价格具有不可预测性;(3)上证指数的对数价格的波动率具有聚集现象,可以认为我国股票市场上呈现出“强 者越强,弱者越弱”的现象。
参考文献
[1] 成城.基于GARCH模型的上证指数波动率特征分析[D].山东大学,2014.
[2] 陈潇,杨恩.中美股市杠杆效应与波动溢出效应——基于GARCH模型的实证分析[J].财经科学,2011(4).
[3] 单瞳.基于GARCH模型的我国股票价格波动性研究——以上证综指为例[D].东北大学,2015.
[4] 孙映宏,曹显兵.基于GARCH模型的中美汇率实证分析[J].数学的实践与认识,2012(20).
[5] 何树红,张秋月,张文.基于GARCH模型的股指期货协整跨期套利实证研究[J].数学的实践与认识,2013(20).
[6] 唐俊波,杨四香,何树红.基于GARCH模型的上证指数实证分析[J].重庆工商大学学报,2012(10).
