共享单车最优选址问题的研究

肖磊 崔悦琪 钟丽 黄薰好

摘 要：为解决共享单车停放问题，改善道路交通拥堵状况，提升城市形象，本文以唐山市万达广场的三个区域进行选址进行研究，利用层次分析法和熵权法对所选区域进行评价，得到一个最优区域，从而运用重心法作进一步选址优化，得出最优位置。这对于共享单车停放区域规划以及类似选址优化问题具有极大的现实参考和指导意义。

关键词：交通规划 层次分析法 熵权法 重心法 最优选址

中图分类号：F724.6 文献标识码：A 文章编号：2096-0298（2018）01（b）-162-02

随着共享经济和移动互联网的飞速发展，共享单车应运而生，因其符合低碳出行理念，具有轻巧灵活、使用便捷等优势而被广大群众所青睐。然而，随着各地共享单车拥有量的急剧增大，出现了车辆摆放混乱、占用人行道、损坏丢失等一系列问题，严重影响了市容市貌，也造成了交通拥堵。因此，合理规划共享单车停车区域，选取最优的停放位置，改善城市交通拥堵状况，提升城市形象是一个刻不容缓的问题。本文以层次分析法和熵权法为基础，以重心法为核心，研究了共享单车最佳的选址位置，旨在为市民提供一个快捷合理的停车中心，使其更好地服务于广大用户。

1 共享单车停放区域的选取

1.1 区域的选取

以唐山市万达广场为中心，根据其周边的交通情况和人流量作为重要指标，选取三个主要区域为研究对象，如图1所示。

1.2 层次分析法

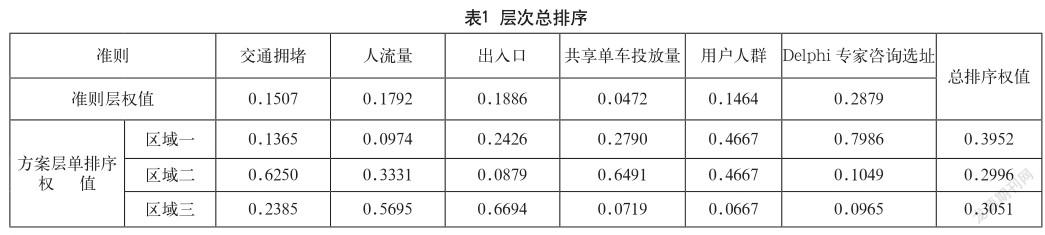
层次分析法[1]作为一种实用的多准则决策方法，既能把一个复杂问题表示为有序的递阶层次结构，通过人们对决策方法的判断进行优劣排序，又能将问题进行定性和定量相结合的分析。以“选取最优的停车区域”为目标层；“交通拥堵”“人流量”“出入口”“共享单车投放量”“用户人群”“Delphi专家咨询选址”六个指标为准则层；“区域一”“区域二”“区域三”三个区域为方案层。

2 模型求解

2.1 区域的计算

通过层次分析法计算得到总排序结果，如表1所示。

对于选取的各指标，运用熵权法对其进行客观权重求解，结合表1中层次分析法所得到的总排序权值，再利用公式（5）求出层次分析法和熵权法两者相结合的权重，最后得到最终权重值如表2所示。

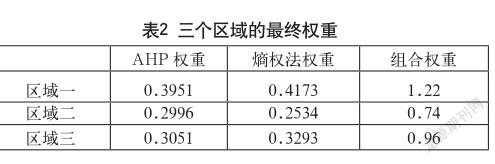
由表2可知，区域一的组合权重最大，说明区域一是最优的停车区域。

2.2 区域的优化

通过Delphi专家咨询选址将区域一划分为A～I这9个小区块，如图2所示。

2.2.1 确定各区块的中心坐标

选取一点O为坐标原点建立平面直角坐标系，通过区块图测得9个小区域中心坐标：

A（-6.15，3.79）B （-3.99，5.00）C（-4.12，1.50） D（0.80，5.88） E（0.62，3.63）F（0.70，1.50） G（7.13，2.68） H（-5.32，-5.75）I（3.81，-5.75）

2.2.2 統计各个小区域的人数

选择工作日和周末各一天，从8：00～22：00时间段统计到达各个小区域停取共享单车的用户人数，并将各个时间段内各个区域的用户分别求和后求均值，最后结果如表3所示。

通过计算可得最佳位置坐标为（-1.545，-0.349），优化后位置在区域F下方，乘以真实比例换算后得出最优位置为：原点0向南移63.377m，向东移13.024m，以原点0为中心，半径为40m为辐射范围的中心区域。

3 结语

本文选取唐山市万达广场的三个区域为研究对象，利用层次分析法和熵权法对所选区域进行评价，通过计算层次分析法和熵权法的组合权重，将两者的权重值结合起来得到区域一为最优的停车区域。然后以选出的最优区域作为研究对象，将区域一进行分块，利用重心法进一步得到区域一中的最佳停车位置，将其作为共享单车的停放点。层次分析法和熵权法的结合使用，不仅可以避免计算结果太过主观或太过客观的情况，还能减小计算误差，使所得结果的可利用性更大。

参考文献

[1] 刘江.基于层次分析法的企业运输方式的选择[D].对外经济贸易大学，2006.

[2] 申志东.运用层次分析法构建国有企业绩效评价体系[J].审计研究，2013（02）.

[3] 张佳钰.熵权法下“互联网+农业”上市公司经营绩效评价[D].沈阳农业大学，2017.

[4] 费智聪.熵权—层次分析法与灰色—层次分析法研究[D].天津大学，2009.