煤层气产能预测新模型

王琰琛 陈 胜 孙兰兰

1.中国石化胜利石油工程公司井下作业公司, 山东 东营 257091; 2.中国石油西部钻探工程有限公司钻井工程技术研究院, 新疆 克拉玛依 834000; 3.中国石化胜利油田分公司胜利采油厂,山东 东营 257091

0 前言

煤层气藏是典型的非常规油气藏,天然裂缝发育[1-5],一般通过压裂等方式进行储层改造后开发。由于煤层气的吸附、解吸和扩散特征,其渗流机理异于常规气藏渗流机理。煤层中的甲烷通过解吸、扩散、渗流三个重要过程而产出,其稳产阶段主要发生在中后期,该阶段大量产气少量产水[6]。目前,国内外针对煤层气产能的研究大多采用数值模拟方法[7-10],鉴于煤层气吸附、解吸和扩散的特征,常规气藏产能预测模型并不适用[11-13],且运用常规二项式产能方程来分析煤层气藏稳态产能会产生较大的误差[14-17],故煤层气藏近似单相产气阶段的流动机理和产能分析具有较高的研究价值[18-20]。本文根据天然裂缝发育型煤层气藏的地质特点,运用平行板理论和等效渗流阻力原理,建立符合其渗流特征和开发模式的稳态产能分析模型,以此模型为基础进行各种特征参数以及模型简化分析,为煤层气藏产能预测和分析提供参考。

1 模型建立

针对天然裂缝发育型煤储层,运用平行板理论建立模型。图1为其中任意一个立方体特征单元,其长、宽、高分别为a,b,h。其中发育垂直裂缝,裂缝宽度为bf,裂缝贯穿整个单元体,高度为h,裂缝线密度为Df,基质宽为bm。煤层气稳态条件下,产量恒定。单元体产量和压力运用等效渗流阻力法原理进行分析。假设裂缝渗透率,基质渗透率和基质中气体扩散系数存在各向同性,分别为kf,km和D。不同方向基质-裂缝系统串并联方式不同,此时应对三个正交方向分别进行分析,其中x和z方向相同,因此下面进对x和y方向进行分析。

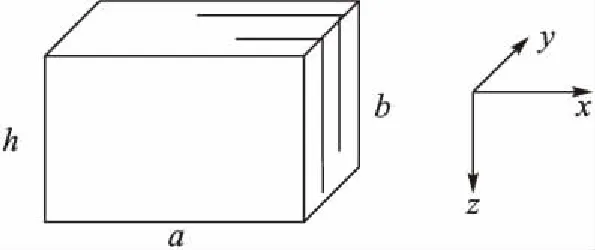
图1 裂缝型煤层气藏特征单元

Qt=Qf+Qm

(1)

其中,裂缝中气体流动符合达西定律,则由达西定律得到裂缝中流量Qf为:

Qf

(2)

基质中主要为解吸扩散流动,且稳态条件下,假设解吸量与基质扩散量相等,认为基质与裂缝之间同时存在气体窜流,则基质产气量Qm等于解吸量Qd和窜流量Qc两部分产量之和,其中:

Qd=bm

(3)

Qc=6bm

(4)

Qm=bm

(5)

由于解吸量等于向外的扩散量,由兰格缪尔等温吸附方程可得:

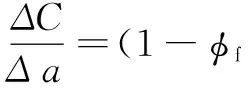
(6)

带入式(5)得到:

Qm=bmhDx(1-φf-φm)VL

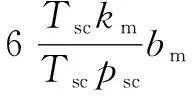
(7)

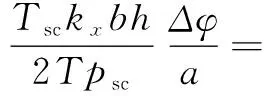
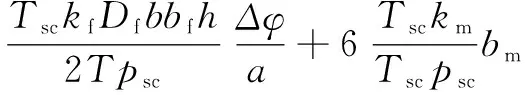
(8)

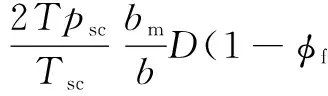
kfDfbf+12km

(9)

kd-φm)VL

(10)

结合孔隙度定义可以得到:

φfbf

(11)

进一步得到:

kx=kd+12km+(kf-kd-12km)φf

(12)

kz=kd+12km+(kf-kd-12km)φf

(13)

Δp=Δpf+Δpm

(14)

基质内部可以看成是解吸扩散和窜流两种方式并联,基质内部产气量结合等值渗流原理得到:

Q=ahD(1-φf-φm)VL

(15)

进一步对基质-裂缝系统运用等效渗流阻力原理,得到基质—裂缝系统串联方程为:

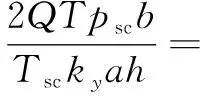
(16)

最终化简得到:

(17)

2 IPR曲线影响因素分析

煤层气藏大多为压裂直井开发,假设压裂形成的垂直裂缝无限导流,裂缝完全贯穿储层,且储层厚度为h,裂缝半长为xf,气藏泄气半径re。基于以上分析可知,等效连续介质理论将煤层气双重介质储层等效为均质储层,结合上文的等效渗透率张量,运用均质储层相关产能模型便能对煤层气产能进行分析。

均质储层中一口无限导流的垂直裂缝压裂井的流场较为复杂,可运用保角变换将其简化为平面带宽为π,排液坑道长为ln(2re/xf)的半无限大地层中平面单向流。再结合等效渗透率张量和达西定律,煤层气稳态条件下,等效均质气藏单向渗流的数学模型为:

(18)

构造新拟压力函数:

(19)

将式(19)带入式(18),并积分得到煤层稳态产能公式为:

(20)

2.1 吸附效应影响

兰格缪尔压力和兰格缪尔体积是表征煤层气吸附特性的参数,选取基本参数:kf=1.35×10-3μm2,D=1.0 cm2/s,re=500 m,xf=90 m,h=10.7 m,φf=0.012,φm=0.059,T=290.15 K,pi=6 MPa。图2为不同兰格缪尔体积VL(20 m3/m3,25 m3/m3,30 m3/m3)和兰格缪尔压力pL(1.5 MPa,2 MPa,2.5 MPa)下的煤层气藏稳态IPR曲线。

考虑煤层气解吸扩散影响时,煤层气藏IPR曲线形状与常规气藏差别很大,曲线呈现下凹,随着兰格缪尔压力的增大,下凹程度变小,IPR曲线逐渐趋于常规IPR曲线,且煤层气无阻流量减小。分析认为当地层压力大于兰格缪尔压力时,煤层气并没有发生解吸,其渗流特征与常规气藏类似,而当地层压力低于兰格缪尔压力时,气体发生解吸,兰格缪尔体积越大,解吸量越大,在相同的生产压差下,气井产量越高。同样，若兰格缪尔体积越大,吸附的煤层气总量越大,在气井敞喷生产时,绝对无阻流量也会越高,随着兰格缪尔体积的减小,下凹程度变大,煤层气无阻流量减小。

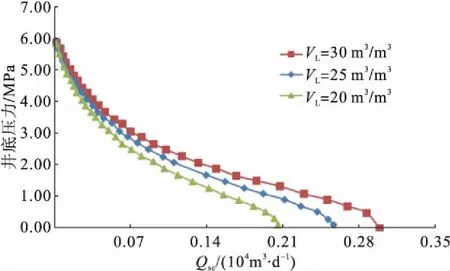
a) 不同VL条件下煤层气IPR曲线

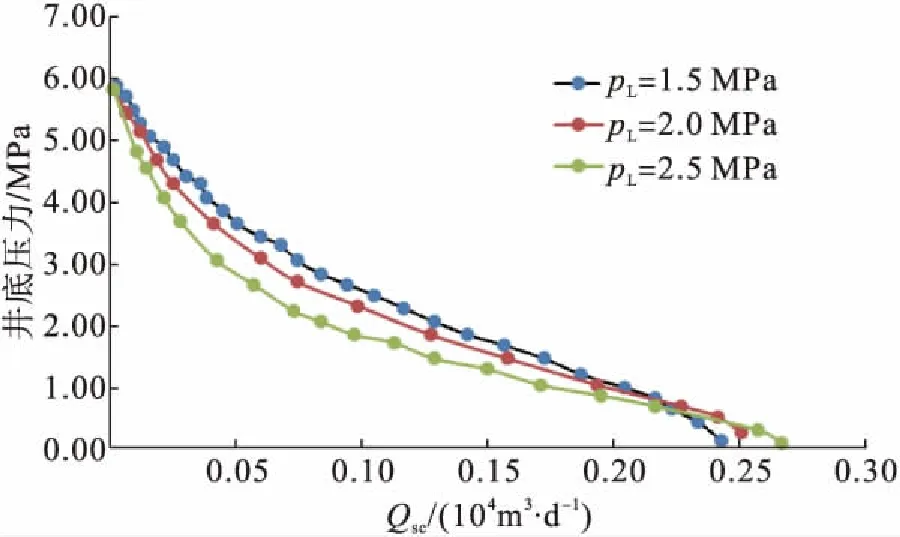
b) 不同pL条件下煤层气IPR曲线图2 兰格缪尔参数对煤层气IPR曲线影响

2.2 扩散效应影响

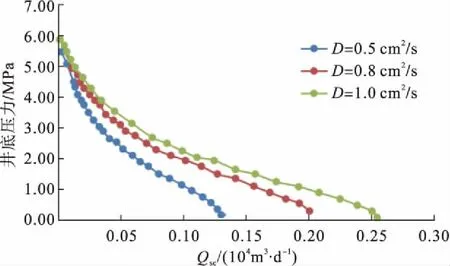
图3 不同扩散系数煤层气IPR曲线

扩散系数越小,煤层气下凹程度越大,绝对无阻流量越小。分析其机理,扩散系数反映气体扩散的能力,扩散项越突出,相对的吸附项对产能的控制变弱,流动供气项(包括渗流和扩散)占主导地位,此时IPR曲线形状接近常规气藏IPR曲线。一般而言,气井敞喷时,扩散系数越大,整体供气能力越强,气井绝对无阻流量越高。

2.3 模型简化分析

实际的煤层气藏是由无数个此模型特征单元组成的,通过该特征模型的流动特性来表征整个煤层气藏的渗流特征。但当模型中的某些参数取特殊值时,该模型可表征不同介质类型的气藏,主要有以下三种情况:

图4为针对上述三种情况做出的IPR曲线。当不考虑煤层气解吸扩散时,其特征与常规气藏形状类似;当考虑基质中气体窜流时,气产量较高,但对产能贡献不大;当考虑煤层气解吸扩散,但忽略基质中气体窜流时,IPR曲线下凹,与常规气藏区别较大,绝对无阻流量也较高;当同时考虑解吸、扩散、窜流流动时煤层气藏整体产能升高,绝对无阻流量最大。

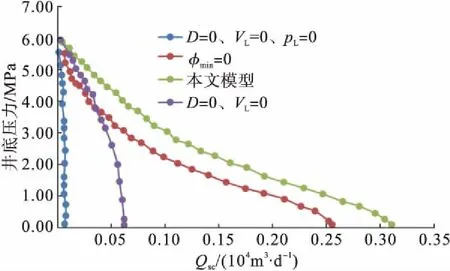
图4 不同简化模型IPR曲线

3 实例分析

选取山西沁水盆地某煤层气区三口气井W 1、W 2和W 3,均为压裂直井,其相关资料数据见表1。运用文中煤层气新模型，结合三口气井实际生产数据,对比分析该模型的精度和适用性。

表1三口煤层气井基本参数表

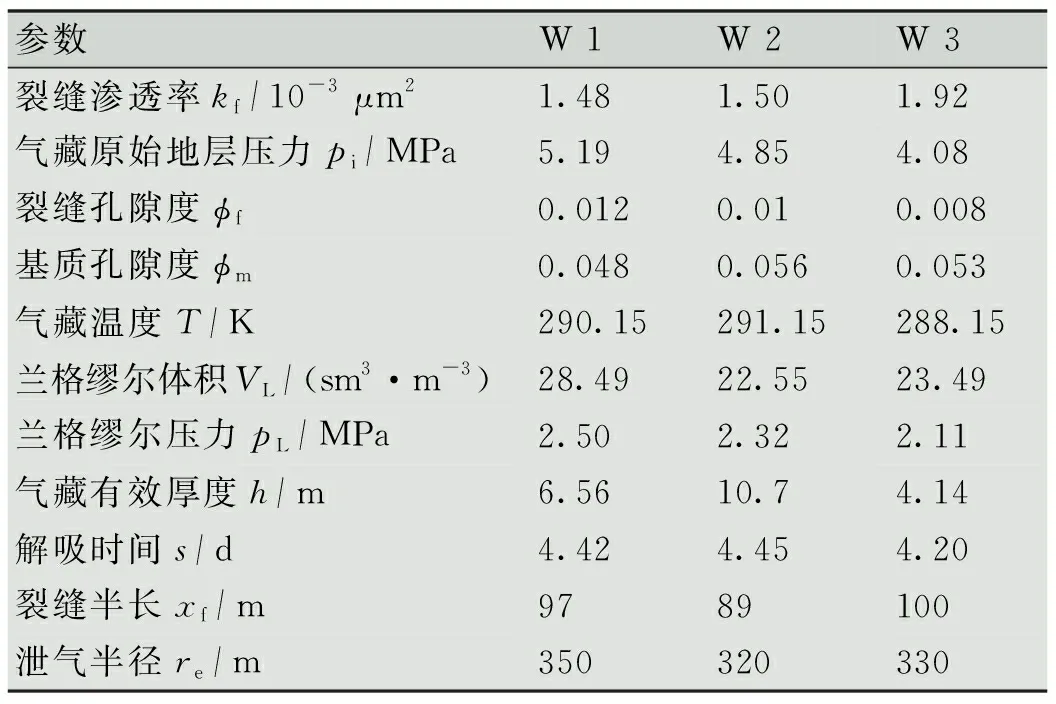
参数W 1W 2W 3裂缝渗透率kf/ 10-3 μm21.481.501.92气藏原始地层压力pi/MPa5.194.854.08裂缝孔隙度ϕf0.0120.010.008基质孔隙度ϕm0.0480.0560.053气藏温度T/K290.15291.15288.15兰格缪尔体积VL/(sm3·m-3)28.4922.5523.49兰格缪尔压力pL/MPa2.502.322.11气藏有效厚度h/m6.5610.74.14解吸时间s/d4.424.454.20裂缝半长xf/m9789100泄气半径re/m350320330

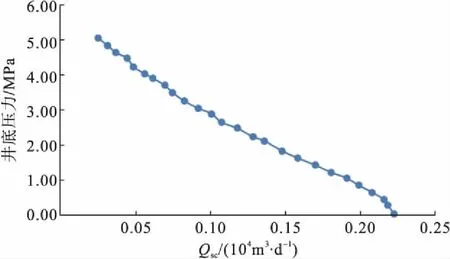
a)W 1井预测生产数据

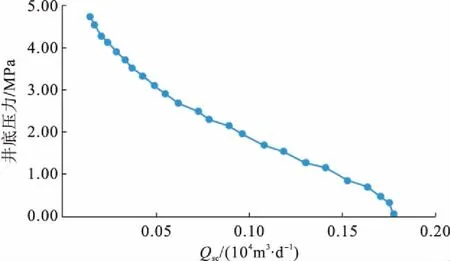
b)W 2井预测生产数据

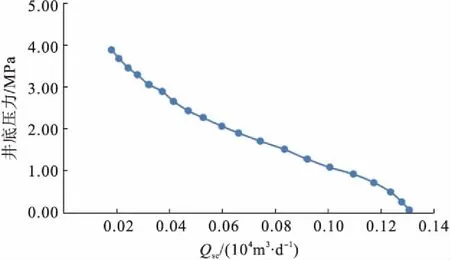
c)W 3井预测生产数据图5 W 1-W 3井预测生产数据

4 结论

1)针对天然裂缝发育型煤层气藏,运用平行板理论以及等值渗流阻力原理,首次建立了符合其渗流特征和开发模式的稳态产能分析模型。

2)考虑煤层气吸附、解吸和扩散影响时,稳态IPR曲线出现下凹的形态,异于常规气藏IPR曲线。兰格缪尔体积越小,扩散系数越小下凹越严重,绝对无阻流量越小；而兰格缪尔压力越小,下凹越严重,绝对无阻流量越大。

3)该模型通过参数赋值,可以转化为各类气藏的产能模型。

4)该模型将双孔煤层气藏等效为均质储层,极大提高煤层气藏产能预测效率,并且通过与实际生产数据对比,该模型具有较高的精度和较强的适用性。