致密储层CO2压裂裂缝扩展规律数值模拟

张健 张国祥 邹雨时 赵文韬 王金意

1 .中国华能集团清洁能源技术研究院有限公司；2.中国石油大学（北京）

目前致密储层压裂多采用滑溜水、线性胶等低黏度水基压裂液，通过高排量和大液量注入提高储层改造体积［1］。但水基压裂液不适用于水敏性、水相圈闭地层，且存在耗水量巨大、化学试剂污染环境等问题［2］。CO2压裂具有节约水资源、降低地层伤害、提高采收率及实现CO2埋存等优点，可避免水基压裂液的环境问题，具有很好的应用前景［3-4］。

国内外学者对CO2干法压裂的研究主要集中于设备、液体等方面［5］，针对其造缝机理研究较为不足。King（1983）［6］研究了低渗透油气田的 CO2干法压裂，指出运用CO2干法压裂可消除渗透率和毛细管力的损害；Settari等（1986）［7］建立了考虑支撑剂沉降和侧向移动影响的CO2干法压裂数值模型，并通过矿场实例验证了其准确性；王斌等（2004）［8］在拟三维模型基础上引入简化的传热模型，建立了CO2干法压裂裂缝扩展数值模型；蒲春生等（2007）［9］基于断裂力学理论，研究了气体压裂的裂缝起裂过程以及增产机理；孙小辉等（2015）［10］研究了CO2压裂的温度场解析模型，但未考虑裂缝扩展；陈立强等（2015）［11］研究了 CO2压裂起裂压力模型，指出黏度、加压速率对起裂压力影响显著。

综上所述，国内外针对CO2干法压裂相关的裂缝扩展数值模拟没有考虑压裂过程的热流固耦合问题，无法准确认识CO2干法压裂裂缝扩展规律。为此，建立了CO2压裂热流固耦合模型，采用有限元法求解，并通过与解析解对比验证模型可靠性。最后采用本文方法对吉林油田致密砂岩CO2干法压裂的主要参数进行了敏感性分析，并给出了考虑热流固耦合的CO2干法压裂的裂缝扩展规律，可为CO2干法压裂提供设计依据。

1 数学模型

CO2压裂裂缝扩展为热流固耦合过程，包括注入流体在裂缝和岩石基质中的流动、岩石变形和CO2压裂液与地层的传热［12］。数学模型即针对这3个物理过程建立。注入流体在裂缝和基质的流动考虑为达西渗流过程［13］；压裂过程注入排量恒定，注入流体井底温度恒定［14］；考虑注入CO2为液态，忽略温度变化对流体黏度、相态的影响［15］。本文应力符号采用弹性力学的规定，即取拉应力为正、压应力为负。

1.1 流体流动方程

水力压裂过程中，裂缝入口不断有液体注入，从而引起裂缝扩展和流体向地层的渗流（滤失）。CO2黏度较低，沿裂缝向地层的滤失较为严重。注入CO2向地层的流动方程为［16］

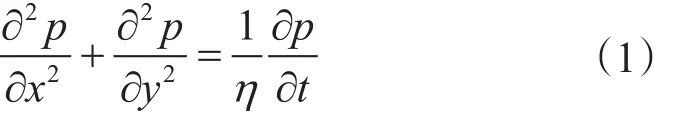
式中，p为流体压力，MPa；η为压力传导系数，m2/s；t为注入时间，s。

式（1）描述了流体在地层的滤失，因此可用于分析CO2压裂过程流体向地层的压力扩散过程。

1.2 热传导方程

由于注入流体CO2温度低于地层温度，水力裂缝扩展过程存在注入流体与地层的热交换问题。根据傅里叶定律和能量守恒原理，可得热传导控制方程为［17］

式中，T为温度，℃；c为温度传导系数，m2/s。

在CO2干法压裂过程中，由于CO2注入流体与地层存在温度差，会产生热应力（温变应力）［18］。根据温度控制方程，可得到地层任一点的温度变化，从而可以计算地层温度变化引起的热应力。考虑地层温度差引起的变形符合线性规律，则温度场变化引起的热应力为［18］

式中，K为体积模量，MPa；ΔT为温度差，℃；β为热膨胀系数，℃-1；δij为克罗内克函数。

1.3 岩石变形方程

各向同性介质中热-孔弹性平衡方程为［19］

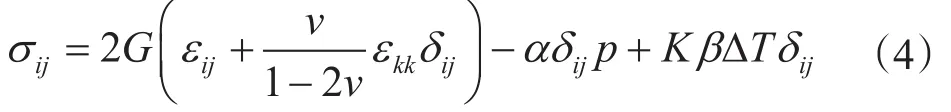
结合岩石变形几何方程，得到固体位移场控制方程为

式中，σij为应力分量，MPa；εij、εkk为应变分量；G为剪切模量，MPa；v为泊松比；α为Biot系数。

1.4 扩展条件

采用最大拉应力准则判断岩石是否发生破坏。当计算单元的应力大于抗拉强度时，岩石发生破坏。最大拉应力准则为

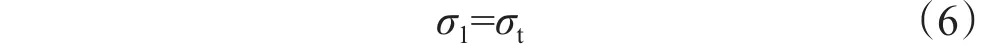
式中，σ1为最大主应力，MPa；σt为岩石抗拉强度，MPa。

1.5 边界和初始条件

（1）流动边界：外边界封闭，内边界（注入位置）恒流量。

（2）热传导边界：外边界绝热，内边界（注入位置）恒温。

（3）应力边界：外边界为远场最大最小主应力，内边界为注入流体压力。

（4）初始条件：地层流体压力为原始地层压力，温度为原始地层温度，初始位移为0。

1.6 模型求解

采用有限元方法求解固体、流体以及热传导方程。方程联立求解较为复杂，本文采用弱耦合方法求解［20］，即首先求解流动方程和热传导方程，再根据压力场和温度场计算应力变化。弱耦合方法在保证一定准确性的基础上，减少了大量迭代计算带来的时间成本问题。计算流程为：首先对模型设置初始值，然后依次求解渗流方程、热传导方程、固体变形方程，然后判断单元是否破坏。如果是，则改变单元的物性参数，如渗透率k、弹性模量E等，并令时间增加预设的增量dt，并再次计算渗流、热传导方程、固体变形方程；否则，则直接令时间增加预设的增量dt，并再次计算渗流方程、热传导方程、固体变形方程。循环该过程，直至达到注入结束时间。程序采用Fortran语言编制，具体计算流程如图1所示。

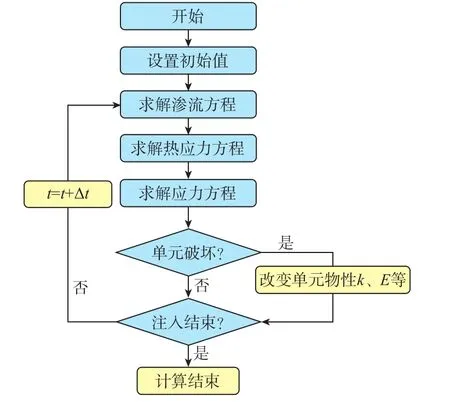
图1 程序计算框图Fig. 1 Block diagram of program calculation

2 模型验证

几何模型如图2所示。模型X方向长度为200 m，Y方向长度为150 m，共划分为60000个三角形单元，30351个节点。

图2 几何模型Fig. 2 Geometric model

为了验证模型的准确性，将数值模型模拟结果与KGD结果［21］进行对比。模型验证中参数取值：黏度为 0.2 mPa·s，排量为 0.05 m3/s，弹性模量为 40 GPa，缝高为50 m。图3为模型计算裂缝扩展动态与解析结果对比，可以看出，模型在不同时刻的缝长和缝宽计算结果与解析解误差均小于5%，满足工程计算精度，表明所建模型可用于裂缝扩展的数值模拟分析。

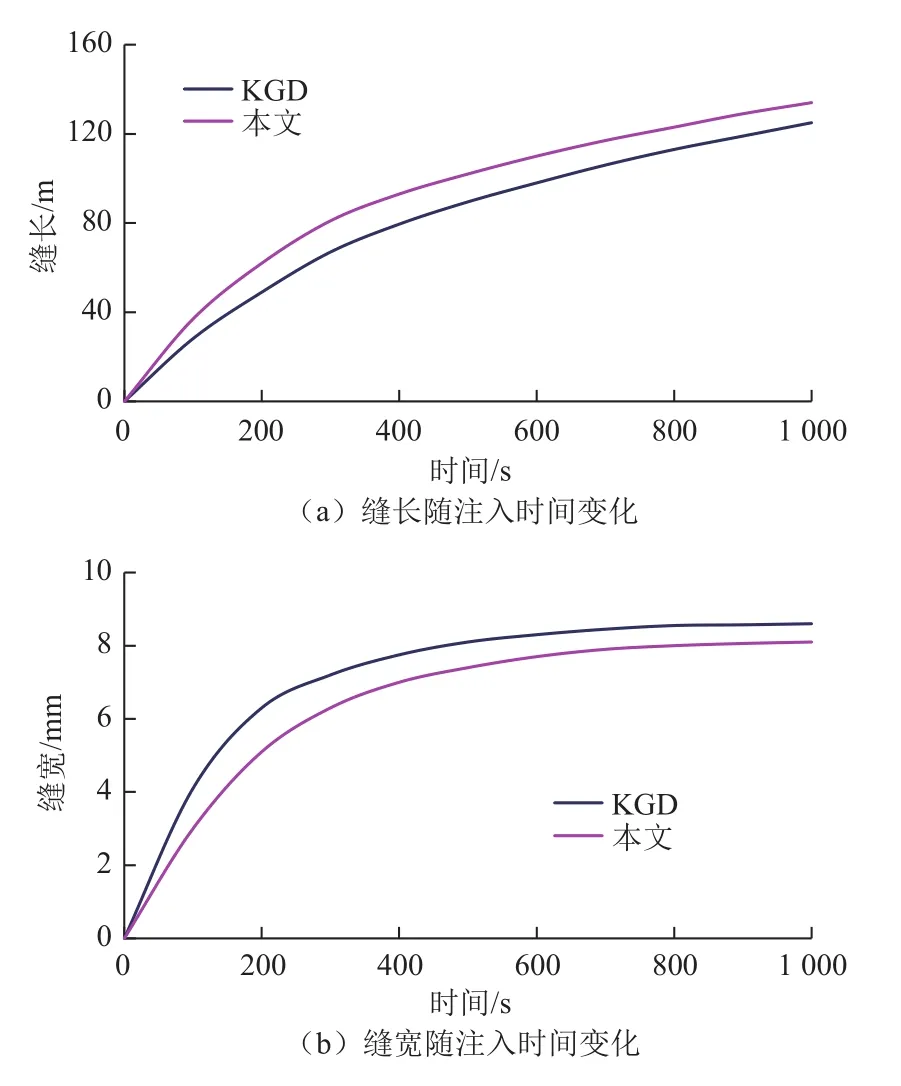
图3 所建模型与KGD模型结果对比Fig. 3 Result comparison between thermo-hydro-mechanical coupling model and KGD model

3 结果分析

为分析CO2压裂裂缝扩展规律，基于第1部分建立的数值模型对地层渗透率、注入液体黏度、排量和地层温度等参数进行敏感性分析。模拟参数（表1）主要基于吉林油田致密砂岩储层X井，渗透率范围为 0.001～0.100 mD，注入黏度为 0.02～1.00 mPa·s，最大施工排量为5 m3/min，注入液温度为地表温度。

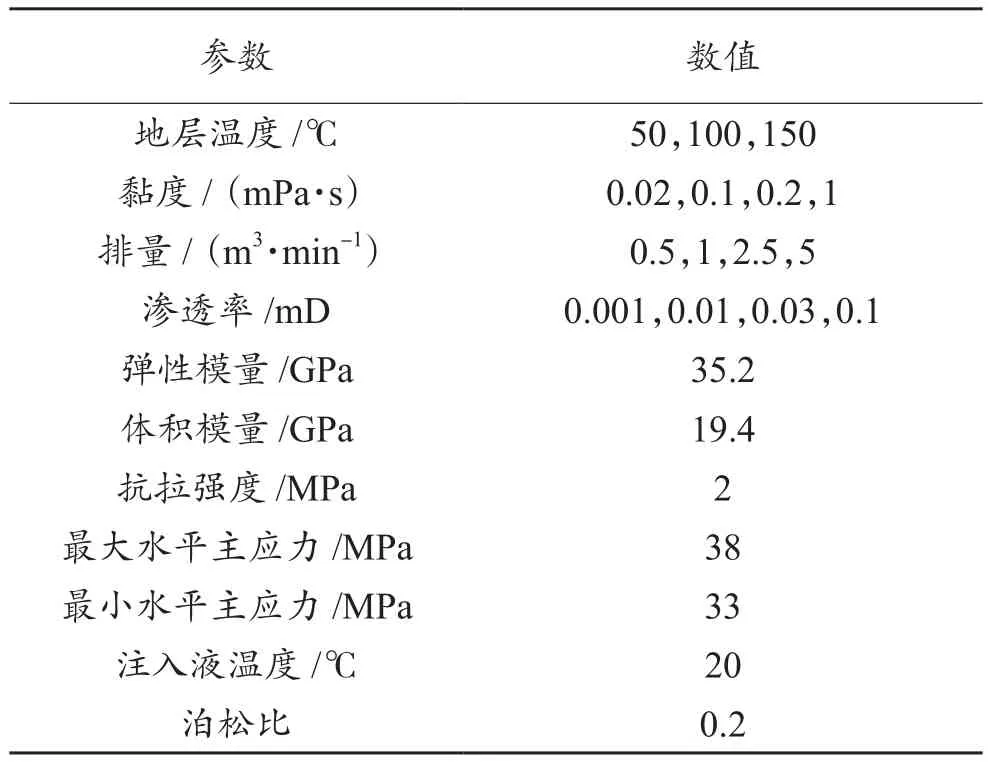
表1 输入参数取值依据Table 1 Valuing basis of input parameters

3.1 渗透率的影响

图4为不同渗透率条件下井底压力变化。图4显示，k=0.001 mD时，地层破裂前增压速率较大，在约100 s时刻发生破裂；k=0.01 mD时，地层破裂前增压速率减小，破裂时刻延后至180 s；k=0.03 mD时，地层破裂前增压速率大幅减小，破裂时刻为780 s；而k=0.1 mD时，地层破裂前增压速率很小，注入1000 s内并没有破裂压力显示。注入时间越长说明注入液量越多，因此，地层渗透率越高，发生起裂需要流体越多。

图4 不同渗透率条件的井底压力随时间变化Fig. 4 Change of bottom hole pressure over the time at different permeability

图5为不同渗透率条件下缝长和缝宽变化，可以看出，k=0.1 mD时，裂缝长度和宽度接近为0，表明裂缝未发生扩展，与井底压力动态吻合。对比不同渗透率的缝长和缝宽变化特征可知，地层渗透率越小，裂缝扩展长度越大，缝宽越大。

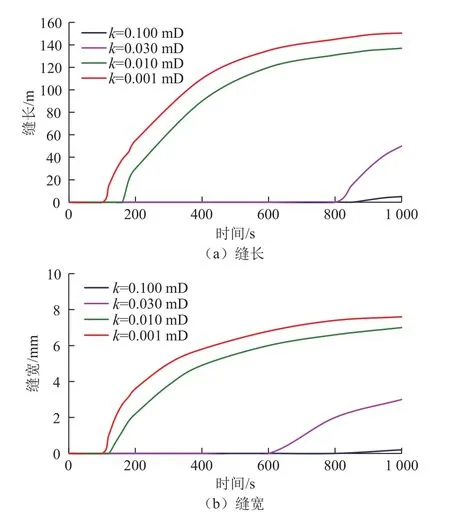
图5 不同渗透率下缝长和缝宽变化Fig. 5 Change of fracture length and wideth at different permeability

图6为注入500 s时刻地层压力分布。对比不同渗透率的压力分布可知，渗透率越大，缝长越短，沿缝长的压力分布范围越小，而垂直于缝长方向的压力扩散范围越大。地层渗透率是影响压力扩散的重要参数，渗透率越大，注入流体沿地层的扩散越快，因此，高渗透地层裂缝起裂时间会延后，滤失量多，进而缝长、缝宽减小。

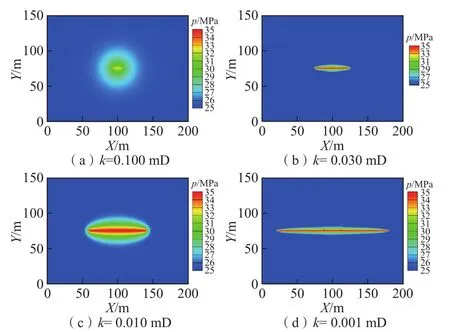
图6 不同渗透率下的压力分布Fig. 6 Pressure distribution at different permeability

3.2 黏度的影响

图7为不同黏度下的井底压力变化，可以看出，黏度为0.1～1 mPa·s时，地层破裂前增压速率基本不变；黏度为0.02 mPa·s，增压速率略微减小。由此可知，对于致密储层，改变注入液体（CO2压裂液）黏度，不会显著影响裂缝起裂时间。该结果与Zhang等［22］考虑液体黏度的裂缝起裂数值模拟结果一致。

图7 不同黏度条件的井底压力随时间变化Fig. 7 Change of bottom hole pressure over the time at different viscosity

图8为不同渗透率条件下缝长和缝宽变化。对于CO2压裂，其他条件相同情况下，注入液体黏度越低，裂缝扩展缝长越短。因此，为解决低黏度液体改造效率过低问题，可适当使用增稠剂增加液体黏度，从而提高液体效率和改造效果低黏度CO2滤失速度较大，压力扩散较为显著，缝内压力耗散较快，因而裂缝长度较短，而增大黏度会减小滤失速度，减缓缝内压力耗散，从而增大裂缝长度。

图8 不同黏度下缝长和缝宽变化Fig. 8 Change of fracture length and wideth at different viscosity

3.3 排量的影响

排量对起裂压力的影响如图9所示，可以看出，当排量为0.5 m3/min时，井底增压速率较小，裂缝在注入约800 s时才开始起裂；随着排量逐渐增加为1 m3/min、2.5 m3/min、5 m3/min 时，注入端达增压速率依次增大。当排量为5 m3/min时，井底压力迅速上升，并在注入约50 s后达到破裂压力，裂缝起裂与延伸速度较快。综合不同排量下井底压力随时间变化情况可知，排量越大，裂缝起裂时间越短。同时，不同排量下，起裂压力均为38 MPa，表明注入排量不影响起裂压力大小。这一现象与起裂压力理论模型结果一致，井筒起裂压力受地应力、井筒形状和地层岩石力学参数影响，与注入参数无关［23］。

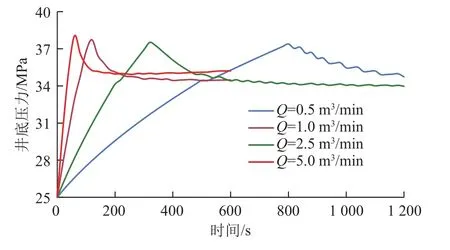
图9 不同排量下井底压力随时间变化Fig. 9 Change of bottom hole pressure over the time at different displacement

图10为不同排量下缝长和缝宽扩展动态。结果显示，排量为0.5 m3/min时，缝长扩展缓慢，最大缝长仅为10 m左右，随着排量增大，缝长和缝宽扩展显著，如排量为5 m3/min时，注入1000 s时缝长达到160 m，缝宽达到8.2 mm。

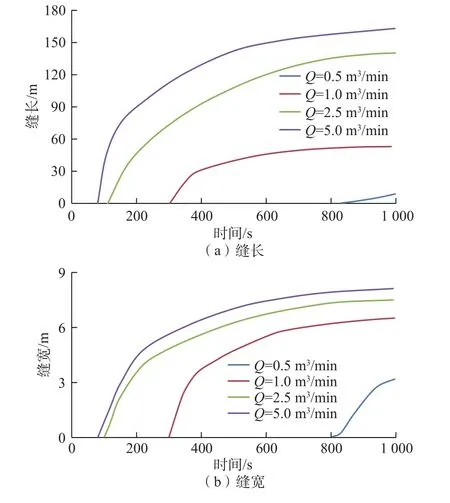
图10 不同排量下缝长和缝宽变化Fig. 10 Change of fracture length and wideth at different displacement

图11为不同排量下压力分布。结果显示，增大排量可导致压力沿缝长扩展，而注入排量较低时，压力主要沿垂直于缝长方向扩散。因此，CO2压裂设计应在考虑设备能力的基础上，尽量提高注入排量，提高裂缝扩展长度和改造体积。在表1参数条件下，适合采用高于2.5 m3/min的排量进行压裂，低于该值时地层破裂前增压速率低，地层不易破裂，形成的裂缝较短且窄，不利于加砂作业。目前CO2干法压裂的砂比一般为1%～4%［24］，压裂后支撑裂缝导流能力较低，导致产能递减较快。

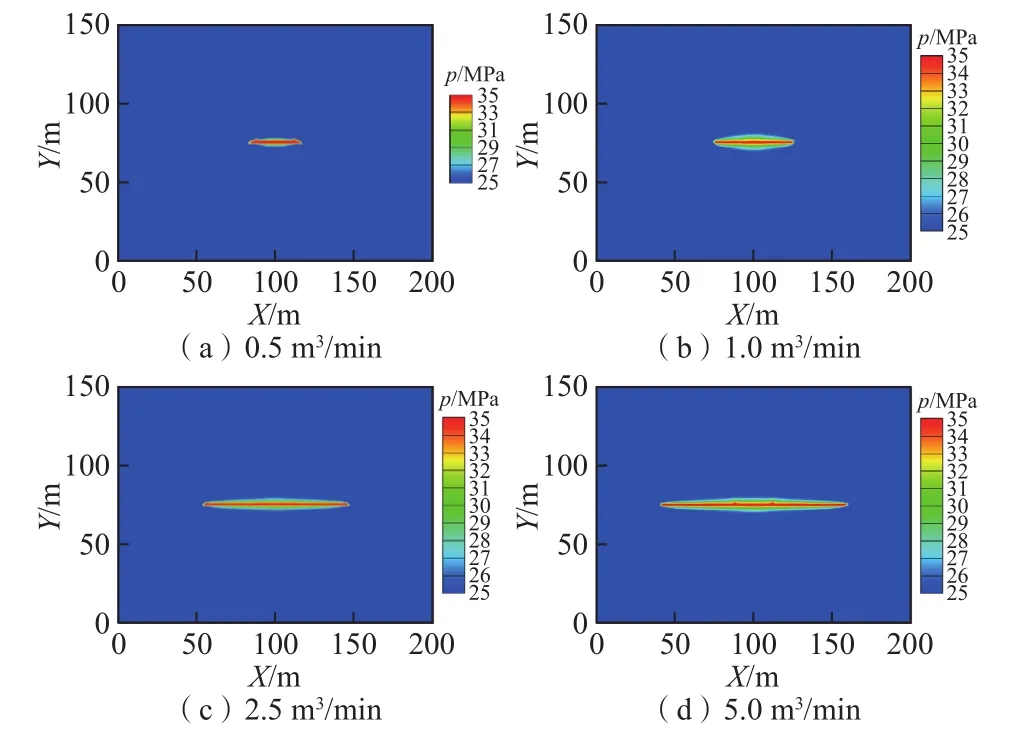
图11 不同排量下的压力分布Fig. 11 Pressure distribution at different displacement

3.4 地层温度的影响

通过模拟不同地层温度下CO2压裂裂缝扩展动态，对比分析热应力对裂缝扩展的作用。图12为不同地层温度条件下井底压力变化动态。结果显示，不考虑温度场作用时，地层破裂压力为39.2 MPa；地层温度50 ℃时，破裂压力为38.3 MPa；地层温度100℃时，破裂压力为36.2 MPa；地层温度150 ℃时，破裂压力为34.5 MPa。因此，相同情况下，CO2压裂液与地层温差越大，发生热交换量越多，地层热应力越大，破裂压力越小，同时破裂时间也有一定程度减小。

图12 不同地层温度下注入压力随时间变化Fig. 12 Change of injection pressure over the time at different reservoir temperature

图13为不同温度条件下缝长和缝宽变化。增大地层温度与注入液温差会促进裂缝延伸，提高裂缝宽度。这是因为温度差越大，地层产生热应力越大，而热应力是拉伸应力，有利于减小裂缝延伸阻力，促进裂缝延伸。该现象与地热井压裂中热应力现场相类似［25］，因此，CO2压裂设计不能忽略地层热应力的造缝作用。

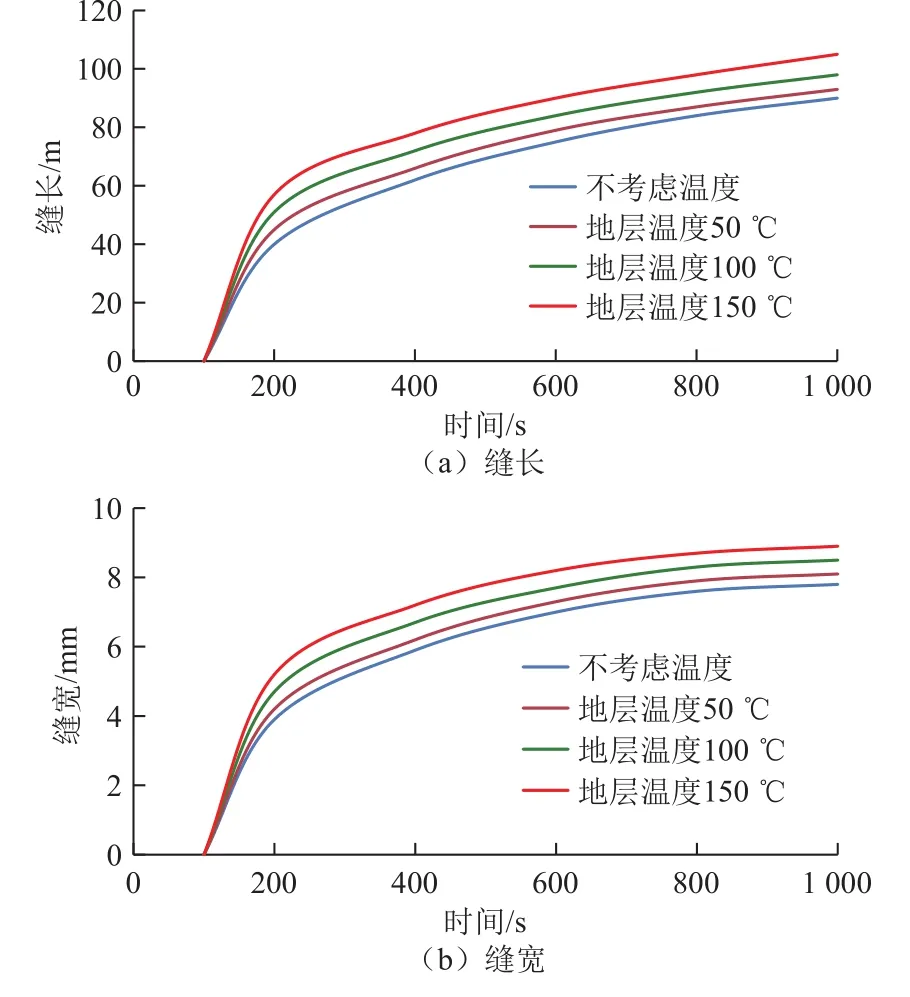
图13 不同地层温度下缝长和缝宽变化Fig. 13 Change of fracture length and wideth at different reservoir temperature

图14为不同地层温度下，注入CO2导致的地层温度场分布。

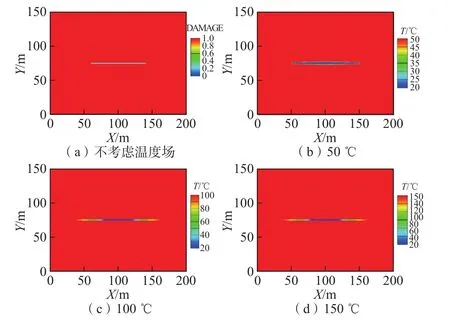
图14 不同地层初始温度的温度场分布Fig. 14 Temperature field distribution correspondind to different initial reservoir temperature

注入CO2导致裂缝附近存在低温区，但由于CO2热传导范围较小，低温区局限于垂直裂缝距离5 m之内。当考虑热应力作用时，裂缝扩展缝长增加。地层温度越高，注入流体与地层温度差越大，裂缝长度增加越大。

4 结论

（1）CO2干法压裂设计需要考虑注入CO2与地层的热传导和热应力作用。地层与注入液的温度差越大，热应力越大，地层发生破裂的起裂压力越小，裂缝延伸越容易。

（2）地层渗透率、注入流体黏度和排量是影响CO2干法压裂流体滤失的关键因素。渗透率较高储层（k＞0.01 mD）不适合低黏度CO2压裂；CO2低黏度特性导致滤失速度较大，压力扩散显著，裂缝长度较短、宽度较小。

（3）CO2干法压裂地层起裂压力大小不受排量和黏度显著影响，但排量和黏度会改变起裂时间和延伸压力。