基于最小耗能原理的岩石损伤本构模型研究
2018-09-07孙梦成徐卫亚王苏生王如宾王伟
孙梦成,徐卫亚,王苏生,王如宾,王伟
基于最小耗能原理的岩石损伤本构模型研究
孙梦成1, 2,徐卫亚1, 2,王苏生1, 2,王如宾1, 2,王伟1, 2
(1. 河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京,210098;2. 河海大学 岩土工程科学研究所,江苏 南京,210098)
在连续损伤理论框架下引入最小耗能原理,将岩石统一能量屈服准则作为耗能约束条件,基于各向同性基本假定构建一种新型损伤本构模型。假定以岩石初始屈服点作为损伤阈值,模型考虑损伤阈值对损伤演化规律的影响;推导岩石三轴压缩强度和变形参量与模型参数的理论关系。为验证模型的合理性,对角砾熔岩进行不同围压下的常规三轴压缩试验,并分析破坏过程中岩石变形各阶段的能量演化特征。研究结果表明:该模型能较好地反映岩石材料在复杂应力条件下的非线性力学行为,且考虑损伤阈值影响的模型对岩石后屈服段的拟合精度更高,对复杂应力条件下的岩石工程安全分析具有参考价值。
岩石力学;最小耗能原理;岩石统一能量屈服准则;损伤阈值;损伤演化方程
漫长的地质演变过程及复杂的三向应力环境使岩石内部产生大量非连续且形态不规则的隐裂隙、微裂纹、微孔洞及节理等微缺陷,微缺陷在不同应力条件下的力学响应决定其显著的宏观非线性力学特性[1]。大量岩石高边坡及大型地下洞室开挖工程实践表明,岩石的力学特性对岩土结构的安全设计和稳定性分析尤为重要[2−3],因此,构建岩石在复杂应力状态下的非线性力学本构模型历来是岩土界的研究热点之一。为了准确反映岩石的非线性本构关系,基于有效应力概念和LEMAITRE等效应变假说[4],引入损伤变量构建损伤本构模型已发展成研究岩石本构关系的一种重要方法。韦立德等[5−7]假定岩石内部微缺陷随机分散,岩石微元强度服从概率分布,结合连续损伤理论和统计规律,构建了可描述岩石应变软化特性的弹塑性统计损伤本构模型;曹瑞琅等[8−10]基于体积变化和峰后残余强度对损伤变量的影响,修正模型参数并考虑损伤阈值,使岩石统计损伤本构研究得到进一步发展。但岩石损伤同时受材料内的微缺陷和岩石微元所受应力状态的影响,上述模型存在一定的局限性。岩石变形破坏的实质是其内部能量耗散和释放的过程,能量耗散是损伤逐步发展的内动力[11],为更深层次地分析岩石破坏过程的能量耗散与损伤演化的关系,众多研究者从能量角度对岩石非线性力学特性展开研究并取得了许多成果。刘天为等[12−13]开展了岩石室内三轴压缩试验,通过计算加载各阶段的能量转换量,研究了岩石加载变形过程的能量耗散规律;谢和平等[14−17]在不可逆热力学框架下,基于能量耗散原理推导了损伤演化方程并建立了岩石损伤本构;依据岩石损伤演化的能量耗散过程符合最小耗能原理的客观规律,高玮 等[18−19]运用最小耗能原理研究了花岗岩在单轴压缩下的损伤演变规律,为岩石损伤研究提供了一条新路径。可见,研究复杂应力条件下岩石的非线性本构关系时,很少将最小耗能原理运用于岩石损伤演化方程的建立,已有基于能量原理的损伤本构中较少考虑损伤阈值的影响。鉴于此,本文作者基于最小耗能原理和连续损伤理论,引入岩石统一能量屈服准则为耗能约束条件,建立基于最小耗能原理的新型损伤本构模型。此外,对角砾熔岩开展不同围压下的常规三轴压缩试验,结合试验结果分析岩石变形各阶段的能量转换关系,在此基础上验证所建损伤本构模型的合理性。
1 岩石损伤本构模型
1.1 损伤演化方程推导
岩石内部从萌生初始裂隙到贯通为宏观裂纹导致整体破坏,其实质是损伤变量逐渐增大,直至临界值的过程。岩石损伤演化伴随着能量的不可逆耗散,在封闭无热交换的系统内,岩石单元耗散能d满足:
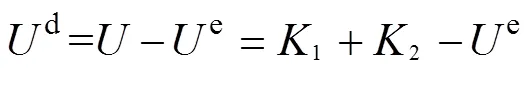
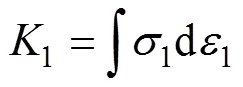
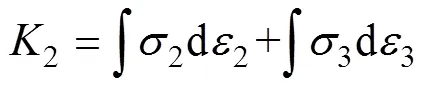
式中:为岩石单元总应变能,由试验机压缩岩样作功1和岩样沿径向变形压缩液压油作功2组成;e为岩石单元可释放弹性应变能;和(=1,2,3)为岩石单元的名义主应力和主应变。
在常规三轴应力状态下(2=3),假定加载中岩石损伤为各向同性且泊松比不受损伤影响,即1=2=3=,1=2=3=(其中,为损伤岩石的卸载弹性模量,为材料损伤前的名义泊松比)。将泊松比=−3/1代入式(1)~(3)得

在岩石三轴压缩试验中,通常先施加围压到预设值,再施加轴向应力至岩样破坏。现阶段计算单元应变能时一般不考虑施加轴向应力前岩石在围压作用下产生的初始应变10和初始应变能0,为精确反映岩样在各阶段的能量转换特征,结合式(4)对岩石应变能进行修正,得到岩石单元实际应变能1:
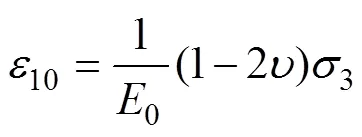

式中:10为初始压密段的初始应变;0为岩石损伤前的初始弹性模量。在主应力空间中,岩石单元可释放弹性应变能[17]为

式中:为岩石的卸载弹性模量。为简化数值分析,取初始弹性模量0代入计算。
结合式(6)和式(7),整理得常规三轴应力状态下的岩石单元耗散能为
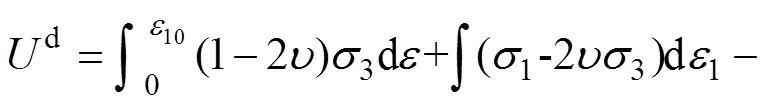

在岩石损伤破坏各阶段,将系统的热力学变化看作是一种平衡被打破和重建的过程。当岩石内产生裂隙时,当前平衡状态被打破;当能量耗散趋于稳定时,系统处于新的平衡状态。因此,岩石的损伤演化是符合最小耗能原理的能量耗散过程,可以通过研究能量耗散率分析损伤演化规律。
最小耗能原理[20]指出:所有耗能过程都在对应的约束条件下沿最小耗能路径进行。“沿最小耗能路径进行”指瞬时耗能率对应于耗能过程的任何时刻均为最小值,物理变量需满足的控制方程即耗能约束条件。
在弹性损伤模型中,假定损伤产生的不可逆应变为岩石破坏过程中的唯一耗能机制,材料耗能率定义为
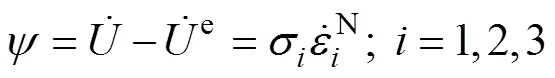

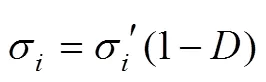


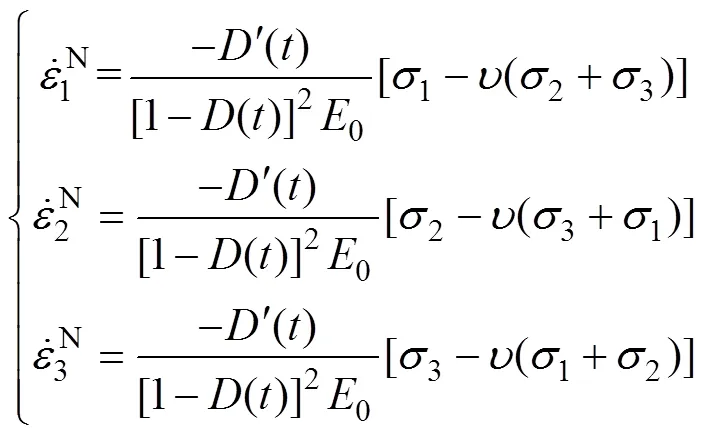
将式(11)代入式(9),耗能率可表示为

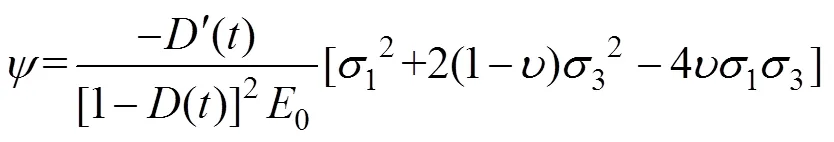

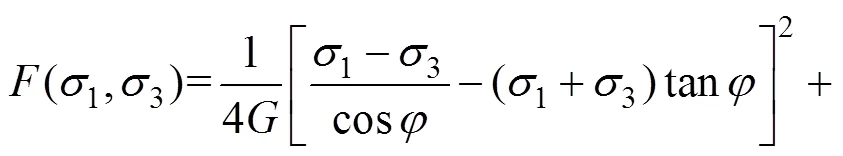
式中:和为材料参数,表征岩石初始屈服时剪切应变能与体积变形能的数值关系;为内摩擦角;和分别为剪切模量和体积模量。
根据最小耗能原理,在材料耗能损伤过程的任意时刻,耗能率都在对应耗能约束条件下取驻值,引入待定Lagrange乘子*,可表达为

结合式(13)~式(15),推导得损伤演化方程为

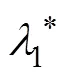
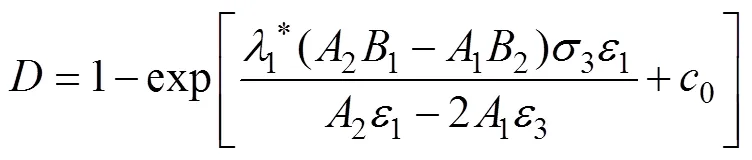
岩石损伤存在阈值问题[9],岩石损伤当应变达到阈值后开始发展,在损伤阈值前处于线弹性变形阶段。因而,需要考虑损伤演化规律的阈值影响,引入损伤阈值应变0后的损伤演化方程表示为
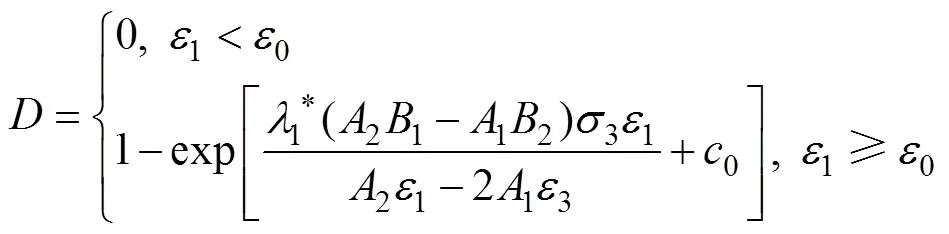
对于常规三轴压缩试验,试验实测轴向偏应力1t为实际轴向表观应力1与围压3的差值,表示为

为真实反映应力−应变关系,需要考虑岩石初始压密过程,根据式(5)和实测应变1t将轴向表观应变1修正为

将式(18)~(20)代入式(10),得基于最小耗能原理的岩石损伤本构为

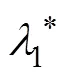
1.2 损伤阈值确定和模型参数辨识
损伤阈值通常需要借助CT实时细观试验或声发射技术来进行定量分析。EBERHARDT等[22]研究花岗岩的脆性破坏特性时,定义损伤阈值为体积应变−轴向应变曲线驻点处的应力水平,并分析了花岗岩损伤阶段的力学参数演化规律。鉴于岩石在体积扩容起始点之后,岩石内部产生塑性变形且力学性质开始弱化,为简化分析,将初始屈服点与体积扩容应力点建立联系,并确定体积扩容点为损伤阈值。根据角砾熔岩在不同围压下的三轴压缩试验结果,确定体积应变−轴向应变曲线驻点处的轴向应变为损伤阈值应变0。
考虑角砾熔岩在低围压下的应变软化特征,采用岩石应力−应变曲线的峰值点强度辨识模型参数,使参数具有明确的物理含义。假定围压下岩石的应力−应变曲线峰值点处应力、轴向应变和径向应变为s,1s和3s;由应力−应变曲线的极值性,在峰值点处,有

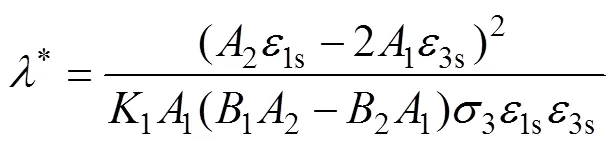
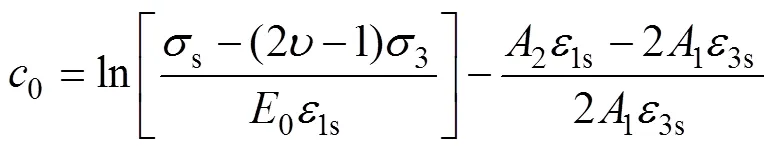
2 角砾熔岩三轴压缩试验及能量演化特征
2.1 角砾熔岩三轴压缩试验
角砾熔岩三轴压缩试验在河海大学岩石流变力学实验室岩石三轴伺服测试系统上完成,对角砾熔岩岩样开展围压为6,8,10 MPa的常规三轴压缩试验。按照国际岩石力学学会(ISRM)标准[23],将角砾熔岩原状样打磨成直径×高度为50 mm×100 mm的标准圆柱体,所选岩样的均匀性和完整性均满足试验规范,对应于围压6,8和10 MPa下的岩样编号分别为B-J-01,B-J-02和B-J-03。角砾熔岩试样如图1所示。
试验以轴向位移控制方法实施,先按静水压力条件施加围压至预设值,待围压施加完毕并稳定后按0.02 mm/min速率施加轴向偏压至岩样破坏。在整个加载过程中,伺服测试系统自动记录施加的轴向荷载,并由安装在压力室底座的2个高精度LVDT和固定在试样上的1个应变测量环分别记录轴向和径向变形量。

围压/MPa:(a) 6;(b) 8;(c) 10
图2所示为破坏后的岩石试样。从图2可看出:岩样在三轴压缩应力路径下均为单截面剪切破坏,且在低围压状态下由于围压对岩样径向约束作用较弱,破坏时岩样两端易于产生张拉性裂纹;在高围压下,因静水压力约束试样径向膨胀变形,抑制了岩样内部张性裂隙的发育和扩展,其破坏形式主要为剪切滑移破坏。

围压/MPa:(a) 6;(b) 8;(c) 10
按照上述试验方案,对角砾熔岩开展常规三轴压缩试验得到应力−应变关系曲线和体积应变−轴向应变曲线,分别如图3和图4所示。从图3可见:随着围压增加,抗压强度分别为147.04,170.10和185.95 MPa,表明初始围压的增加能够显著提高岩石的强度;在初始围压下,岩样内部微裂隙逐渐闭合且颗粒骨架更密实;此外,加载时围压作用限制岩石内原生裂隙面间的摩擦滑移,使内部裂纹贯通更困难,增强了岩石抗压能力。根据室内三轴压缩试验结果,整理得出角砾熔岩的力学强度参数如表1所示。
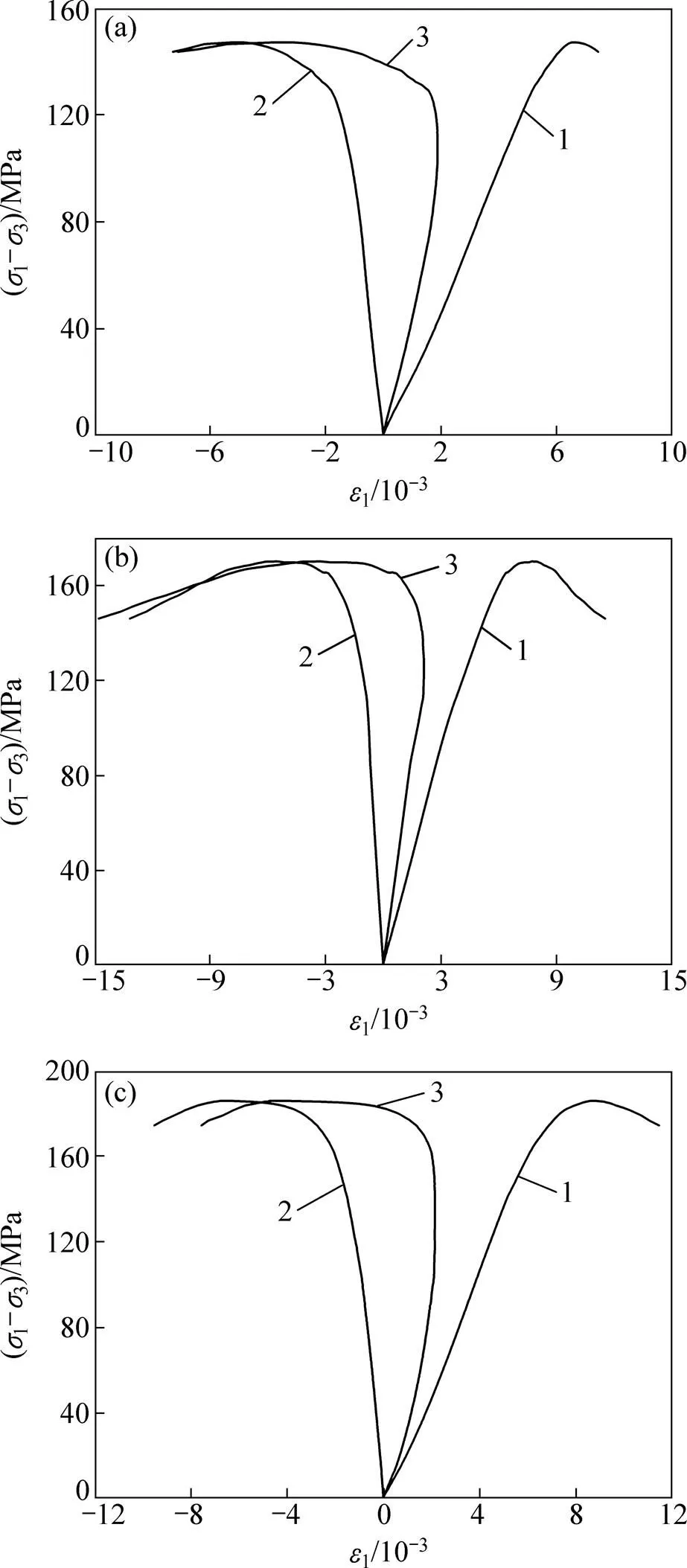
围压/MPa:(a) 6;(b) 8;(c) 10
据图4所示应变关系曲线可确定体积应变−轴向应变曲线驻点为初始屈服点,计算得到不同围压下的角砾熔岩在初始屈服处的剪切应变能与体积应变能近似符合线性关系,表明岩石统一能量屈服准则能较好地描述角砾熔岩的屈服特性,结合试验结果拟合式(14),确定屈服准则(1,3)的材料参数=0.032,=7.960。

围压/MPa:1—6;2—8;3—10。

表1 角砾熔岩常规三轴压缩试验力学参数
注:黏聚力为15.68 MPa;内摩擦角为53.39°。
2.2 三轴压缩角砾熔岩的能量特征
基于能量数值计算原理,采用表1所示的力学参数,计算得到角砾熔岩压缩破坏过程中能量演化与偏应力的关系如图5所示。根据能量演化规律和应力−应变关系,岩石破坏过程可分为4个阶段。
1) 初始非线性段()。岩石单元可释放弹性能U增大速度缓慢,表明加载初期外荷压缩岩样做功主要用于材料内部孔隙闭合和颗粒骨架弹性变形。
2) 线弹性段()。随着偏应力逐渐增大,岩样内部原生裂隙闭合完全,应力−应变关系趋于线性且岩石内部颗粒骨架产生线弹性变形并将外荷做功储存为可释放弹性势能,岩石吸收总能量和可释放弹性能快速增加,耗散能仍不增大。

围压/MPa:(a) 6;(b) 8;(c) 10
3) 破裂发展段()。当应力水平超过初始屈服点后,岩石内部微裂纹快速扩展并产生塑性变形,损伤开始发展导致岩石强度逐渐弱化,岩石呈现出非线性力学特征。可释放弹性能增速变缓并在峰值应力处达到极值而耗散能快速增加,岩石单元总应变能以塑性能、热能等其他形式被耗散。
4) 峰后应变软化段()。随着岩石损伤逐渐加强,内部裂纹不断扩展并贯通为宏观破坏面,能量达到岩石破坏所需的耗散能时快速释放导致岩样整体破坏。
表2所示为不同围压下的角砾熔岩三轴压缩过程的能量特征统计值,对应于峰值强度的岩石单元可释放弹性能和吸收总应变能分别定义为极限弹性能和破坏总应变能。分析表2可知:峰值处耗散能和极限弹性能表现出明显的围压效应,且初始屈服应力也随着围压的增大而增高,B-J-01岩样在初始围压6 MPa下破坏时峰值处耗散能为0.092 MJ·cm−3,极限弹性能为0.393 MJ·cm−3;B-J-02岩样施加初始围压8 MPa,破坏时峰值处耗散能为0.237 MJ·cm−3,极限弹性能为0.434 MJ·cm−3;B-J-03岩样在初始围压10 MPa下,岩样破坏时峰值处耗散能为0.303 MJ·cm−3,极限弹性能为0.521 MJ·cm−3;对应于6,8,10 MPa初始围压下,岩样在屈服阶段损伤发展耗散的能量占破坏总应变能的比例分别为30.75%,48.86%,56.39%。
结合图5分析角砾熔岩的能量演化规律,能量主要耗散于岩石的后屈服变形段,岩石内部损伤随着耗散能的快速增加而开始发展,岩石刚度逐渐弱化;当耗散的能量达到岩石破坏所需的耗散能时,其内部可释放弹性能导致岩样整体破坏,且初始围压愈高,岩石破坏时耗散的能量愈多,在损伤发展阶段耗散的能量占总应变能的比例愈大;在高围压条件下,岩石破坏时内部积累的可释放弹性能越多,发生破坏的程度越剧烈。因此,能量耗散是岩石内部裂隙发展的内动力,能够在分析能量演化规律的基础上,通过研究能量耗散率以分析损伤演化规律。

表2 角砾熔岩三轴压缩的能量特征值
3 模型验证及损伤演化规律分析
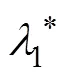

表3 模型参数
将表3中的模型参数代入式(18),得出不同围压下的岩石损伤演化曲线如图7所示。从图7可见:在加载初期,随着应力水平增加,岩石内部的微裂隙和微空洞逐渐闭合且颗粒骨架产生弹性变形,但产生的轴向应变1较小且低于损伤阈值应变0,岩石应力−应变关系基本呈线性关系,损伤变量=0,即岩样在线弹性阶段不产生损伤;随着应力水平进一步提高,当岩样所受应力超过一定水平时,轴向应变1高于损伤阈值应变后损伤开始发展,且损伤变量与轴向应变呈非线性关系;岩石内部的微裂隙快速扩展,局部裂隙密集并贯通产生宏观裂纹,裂纹间经阶梯状连接成主破坏面。根据角砾熔岩的能量演化规律,岩石内部的裂隙发展需要耗散能量,且在屈服阶段耗散能快速增大,当应力水平趋近峰值强度时损伤变量急剧增大,致使岩石刚度显著弱化,表明损伤演化规律与能量耗散规律和试验曲线的非线性特征相符。对比不同围压下的损伤演化曲线发现:随着初始围压增加,对应于不同围压下岩石的损伤阈值逐渐增大,表明围压作用改善了岩石内部受力状态,从而抑制了微裂隙 发展。
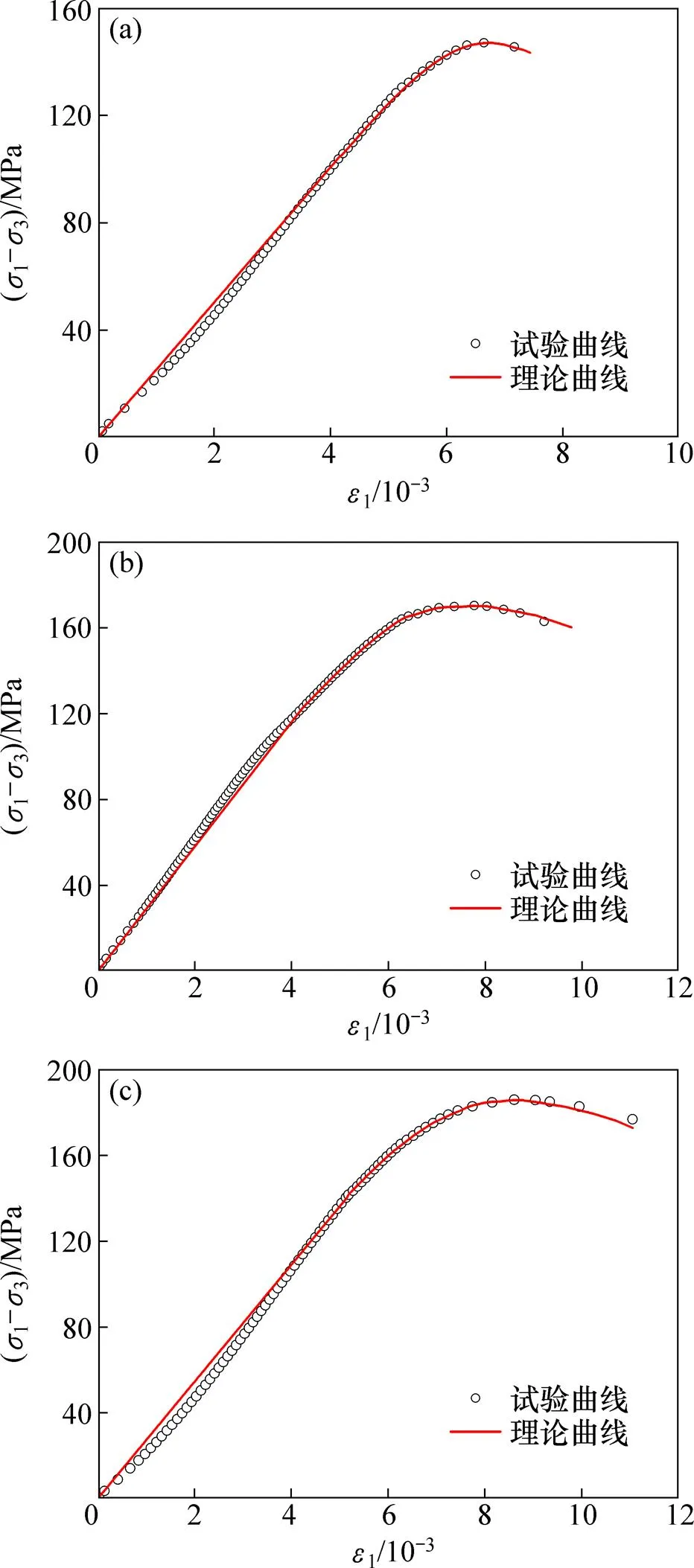
围压/MPa:(a) 6;(b) 8;(c) 10
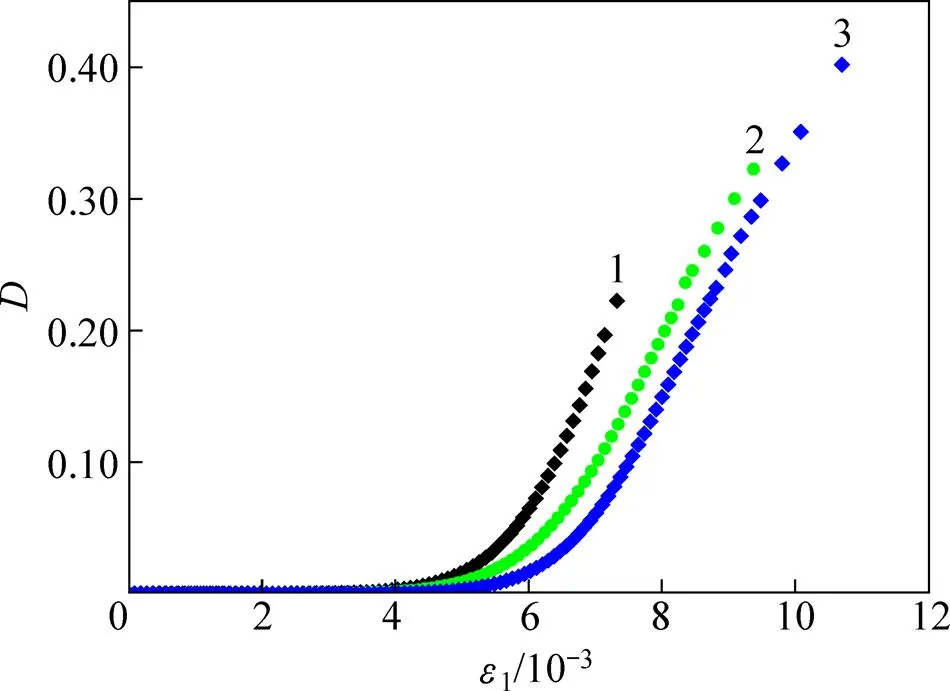
围压/MPa:1—6;2—8;3—10
4 结论
1) 基于连续损伤理论和各向同性假定,运用最小耗能原理导出岩石损伤演化方程,建立了复杂应力条件下的岩石损伤本构模型。对比分析角砾熔岩常规三轴压缩试验结果与理论结果,验证了损伤模型的合理性,表明模型能较好地反映岩石在不同围压下的应力应变关系。
2) 岩石损伤演化的实质是能量耗散。随着围压增加,岩石在损伤发展阶段耗散的能量占总应变能的比例越大,且其破坏时需耗散的能量越多;破坏时,岩石内积累的可释放极限弹性能具有明显的围压效应,初始围压越高,破坏释放的弹性能越多,破坏程度越剧烈。
3) 结合岩石损伤特性考虑损伤演化规律的阈值问题,将岩石的初始屈服点与体积扩容应力点建立联系,以岩石体积扩容点作为损伤阈值,本模型能合理地反映岩石变形前期的线弹性特性和后屈服段的非线性力学行为,更加接近实际情况。
[1] 徐志英. 岩石力学[M]. 3版. 北京: 水利水电出版社, 2007: 69−78.XU Zhiyin. Rock mechanics[M]. 3rd ed. Beijing: Water Resources and Electric Power Press, 2007: 69−78.
[2] 李建林, 王乐华. 节理岩体卸荷非线性力学特性研究[J]. 岩石力学与工程学报, 2007, 26(10): 1968−1975.LI Jianlin, WANG Lehua. Study on unloading nonlinear mechanical characteristics of jointed rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 1968−1975.
[3] 徐卫亚, 宋晓晨, 周维垣. 水电站进水口岩石高边坡及坝坡与洞室相互作用的三维数值分析[J]. 岩石力学与工程学报, 2004, 23(16): 2712−2717.XU Weiya, SONG Xiaochen, ZHOU Weiyuan. Numerical analysis on deformation and stress of high slope of intake and interaction of dam-slope and tunnel at huge hydropower project[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(16): 2712−2717.
[4] LEMAITRE J. How to use damage mechanics[J]. Nuclear Engineering & Design, 1984, 80(2): 233−245.
[5] 韦立德, 徐卫亚, 杨春和, 等. 具有统计损伤的岩石弹塑性本构模型研究[J]. 岩石力学与工程学报, 2004, 23(12): 1971−1975. WEI Lide, XU Weiya, YANG Chunhe, et al. Study on elastoplastic constitutive model of rock with statistical damage[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(12): 1971−1975.
[6] 刘齐建, 杨林德, 曹文贵. 岩石统计损伤本构模型及其参数反演[J]. 岩石力学与工程学报, 2005, 24(4): 616−621.LIU Qijian, YANG Linde, CAO Wengui. Statistical damage constitutive model for rock and back analysis of its parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 616−621.
[7] 杨圣奇, 徐卫亚, 苏承东. 考虑尺寸效应的岩石损伤统计本构模型研究[J]. 岩石力学与工程学报, 2005, 24(24): 4484−4490. YANG Shengqi, XU Weiya, SU Chengdong. Study on statistical damage constitutive model of rock considering scale effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4484−4490.
[8] 曹瑞琅, 贺少辉, 韦京, 等. 基于残余强度修正的岩石损伤软化统计本构模型研究[J]. 岩土力学, 2013, 34(6): 1652−1667. CAO Ruilang, HE Shaohui, WEI Jing, et al. Study of modified statistical damage softening constitutive model for rock considering residual strength[J]. Rock and Soil Mechanics, 2013, 34(6): 1652−1667.
[9] 曹文贵, 赵衡, 张玲, 等. 考虑损伤阀值影响的岩石损伤统计软化本构模型及其参数确定方法[J]. 岩石力学与工程学报, 2008, 27(6): 1148−1154. CAO Wengui, ZHAO Heng, ZHANG Ling, et al. Damage statistical softening constitutive model for rock considering effect of damage threshold and its parameters determination method[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1148−1154.
[10] 王伟, 田振元, 朱其志, 等. 考虑孔隙水压力的岩石统计损伤本构模型研究[J]. 岩石力学与工程学报, 2015, 34(S2): 3676−3682.WANG Wei, TIAN Zhenyuan, ZHU Qizhi, et al. Study of statistical damage constitutive model for rock considering pore water pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S2): 3676−3682.
[11] 谢和平, 鞠杨, 黎立云, 等. 岩体变形破坏过程的能量机制[J]. 岩石力学与工程学报, 2008, 27(9): 1729−1740. XIE Heping, JU Yang, LI Liyun, et al. Energy mechanism of deformation and failure of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1729−1740.
[12] 刘天为, 何江达, 徐文杰. 大理岩三轴压缩破坏的能量特征分析[J]. 岩土工程学报, 2013, 35(2): 395−400. LIU Tianwei, HE Jiangda, XU Wenjie. Energy properties of failure of marble samples under triaxial compression[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 395−400.
[13] 田勇, 俞然刚. 不同围压下灰岩三轴压缩过程能量分析[J]. 岩土力学, 2014, 35(1): 118−122. TIAN Yong, YU Rangang. Energy analysis of limestone during triaxial compression under different confining pressures[J]. Rock and Soil Mechanics, 2014, 35(1): 118−122.
[14] 谢和平, 鞠杨, 黎立云. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J]. 岩石力学与工程学报, 2005, 24(17): 3003−3010. XIE Heping, JU Yang, LI Liyun. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3003−3010.
[15] LIU Xuesheng, NING J G, TAN Yunliang, et al. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading[J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 85: 27−32.
[16] 郭建强, 刘新荣, 王景环, 等. 基于能量原理盐岩的损伤本构模型[J]. 中南大学学报(自然科学版), 2013, 44(12): 5045−5050. GUO Jianqiang, LIU Xinrong, WANG Jinghuan, et al. Damage constitutive model of rock salt based on energy principles[J]. Journal of Central South University (Science and Technology), 2013, 44(12): 5045−5050.
[17] 刘晓明, 熊力, 刘建华, 等. 基于能量耗散原理的红砂岩崩解机制研究[J]. 中南大学学报(自然科学版), 2011, 42(10): 3143−3149. LIU Xiaoming, XIONG Li, LIU Jianhua, et al. Slacking mechanism of red sandstone based on energy dissipation principle[J]. Journal of Central South University(Science and Technology), 2011, 42(10): 3143−3149.
[18] 高玮, 汪磊, 杨大勇. 岩石损伤演化的能量方法研究[J]. 岩石力学与工程学报, 2011, 30(S2): 4087−4092.GAO Wei, WANG Lei, YANG Dayong. Rock damage evolution based on energy principle[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 4087−4092.
[19] GAO Wei, WANG Xu, DAI Shuang, et al. Numerical study on stability of rock slope based on energy method[J]. Advances in Materials Science and Engineering, 2016, 2016: 1−10.
[20] 周筑宝. 最小耗能原理及其应用[M]. 北京: 科学出版社, 2001: 7−10. ZHOU Zhubao. The least energy consumption principle and its applications[M]. Beijing: Science Press, 2001: 7−10.
[21] 周辉, 李震, 朱国金, 等. 基于岩石统一能量屈服准则的硬岩损伤模型[J]. 岩土力学, 2016, 37(3): 609−615. ZHOU Hui, LI Zhen, ZHU Guojin, et al. A damage model for hard rock based on unified energy yield criterion of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 37(3): 609−615.
[22] EBERHARDT E, STEAD D, STIMPSON B, et al. Identifying crack initiation and propagation thresholds in brittle roc[J]. Canadian Geotechnical Journal, 1998, 35(2): 222−233.
[23] ULUSAY R. The ISRM suggested methods for rock characterization, testing and monitoring: 2007—2014[J]. Springer International Publishing, 2014, 15(1): 47−48.
(编辑 陈灿华)
Study on damage constitutive model of rock based on principle of minimum dissipative energy
SUN Mengcheng1, 2, XU Weiya1, 2, WANG Susheng1, 2, WANG Rubin1, 2, WANG Wei1, 2
(1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210098, China; 2. Institute of Geotechnical Engineering, Hohai University, Nanjing 210098, China)
The principle of minimum dissipative energy was introduced based on the continuum damage theory. Taking unified energy yield criterion of rock as the constraints of energy dissipation, a new damage constitutive model was proposed based on the assumption of isotropy. The new damage constitutive model took into account the influence of damage threshold which was assumed to be the starting point of initialyield phase. Furthermore, the theoretical correlation between model parameter and deformation moduli of rock under triaxial compression was deduced. A series of conventional triaxial tests on breccia lava samples were carried out under different confining pressures, and evolution characteristics of energy at different stages of rock deformation and failure were analyzed to verify the rationality of model. The results show that the model can not only reflect the nonlinear mechanical characteristics of rock materials under complicated stress condition, but also has high fitting precision on post-yield stage of rock, which can provide reference for safety analysis of rock engineering under complicated stress condition.
rock mechanics; the principle of minimum dissipative energy; unified energy yield criterion of rock; damage threshold; damage evolution equation
TU452
A
1672−7207(2018)08−2067−09
10.11817/j.issn.1672−7207.2018.08.029
2017−09−08;
2017−11−12
国家自然科学基金资助项目(51479049,51679069);江苏省研究生科研与实践创新计划项目(KYCX17_0471, 2017B700X14)(Projects(51479049, 51679069) supported by the National Natural Science Foundation of China; Project(KYCX17_0471, 2017B700X14) supported by the Postgraduate Research & Practice Innovation Program of Jiangsu Province)
徐卫亚,博士,教授,从事岩土力学与工程研究;E-mail:wyxu@hhu.edu.cn
