时滞系统的自抗扰广义预测控制的性能分析

陈增强，吴瑕，孙明玮，孙青林



时滞系统的自抗扰广义预测控制的性能分析

陈增强1, 2，吴瑕1，孙明玮1，孙青林1

(1. 南开大学 计算机与控制工程学院，天津 300350；2. 天津市智能机器人重点实验室，天津 300350)

为了实现对时滞系统的高性能控制，提出1种自抗扰广义预测控制算法。首先阐述自抗扰广义预测控制算法的设计原理，得到算法的闭环反馈结构。然后利用频域分析法推导出算法的频域特性，分析并总结时滞系统自抗扰广义预测控制算法的参数整定原则。最后对自抗扰广义预测控制算法以及传统的广义预测控制算法的动态性能进行比较。研究结果表明：自抗扰广义预测控制算法无需在线辨识被控对象精确的数学模型，可以离线求得丢番图方程的解析解，算法的在线计算量大大减少；相比于传统的广义预测控制算法，自抗扰广义预测控制算法具有更好的动态性能。

广义预测控制；自抗扰控制；自抗扰广义预测控制；闭环反馈结构；频域分析法

自抗扰控制(active disturbance rejection control，ADRC)是利用PID控制和现代控制理论的先进成果而探索出来的一种不依赖于被控对象精确模型的新型实用数字控制技术[1−3]。其核心思想是将系统的外部扰动以及内部未建模动态综合作为总扰动并将其扩张成一个新的状态，利用扩张状态观测器对其进行实时估计和补偿。因此，自抗扰控制既能有效抑制外界干扰，又可以减弱算法对于模型的依赖,增强了系统的鲁棒 性[4−7]。此前，CLARKE等[8]在保持最小方差自校正控制的在线辨识、输出预测、最小方差控制等特点的基础上，吸收了动态矩阵控制和模型算法控制中的滚动优化策略，提出了广义预测控制(generalized predictive control，GPC)算法。它以受控自回归滑动平均模型(CARIMA)为预测模型，并结合了滚动优化和在线反馈校正等特征，对开环不稳定、非最小相位以及大时滞系统有很好的控制效果。但广义预测控制对被控对象精确的数学模型具有较强的依赖性，且对模型参数较敏感，在线计算量大，限制了其应用范围[8−10]。本文作者针对广义预测控制的不足，提出1种改进的广义预测控制算法—自抗扰广义预测控制算法(ADRC−GPC)。与传统的广义预测控制算法相比，该改进的算法可以离线求得丢番图方程的通解，且无需辨识被控对象的参数，因此，算法在线计算量大大减少。由于广义预测控制算法具有很强的鲁棒性，当被控对象不能被完全转化成积分串联的形式，有一定的误差时，广义预测控制的强鲁棒性仍旧可以保证算法的性能。对于时滞系统，采用忽略时滞的思想来设计自抗扰广义预测控制器[2]。首先介绍无时滞系统自抗扰广义预测控制算法的设计过程。由于自抗扰广义预测控制算法是由连续被控对象和离散控制器组合而成的混合控制算法，难以用时域方法分析算法的稳定性，因此，针对二阶时滞系统，本文作者先将混合系统转化为统一的离散形式，给出闭环控制稳定的条件。之后利用离散域的开环传递函数频率特性，分析算法中各参数的变化对算法性能的影响，获得控制器参数调整的原则与规律；在此基础上，比较ADRC−GPC和GPC这2种算法的动态性能，为ADRC−GPC算法的推广应用提供参考依据。

1 自抗扰广义预测控制算法的设计

1.1 自抗扰广义预测控制的结构

ADRC−GPC运行机理如下：首先将系统的外部扰动以及内部未建模动态综合在一起看成总扰动或扩张状态，并利用扩张状态观测器(extended state observer，ESO)，采用输出反馈的方式对扩张状态的实时作用量进行在线估计和补偿，使得被控对象被转化成标准的串联积分器的形式。针对串联积分器模型设计广义预测控制律，以达到控制目标。只需要知道系统的阶次以及对总扰动的估计信息+1，就可以完成ADRC−GPC控制器设计。

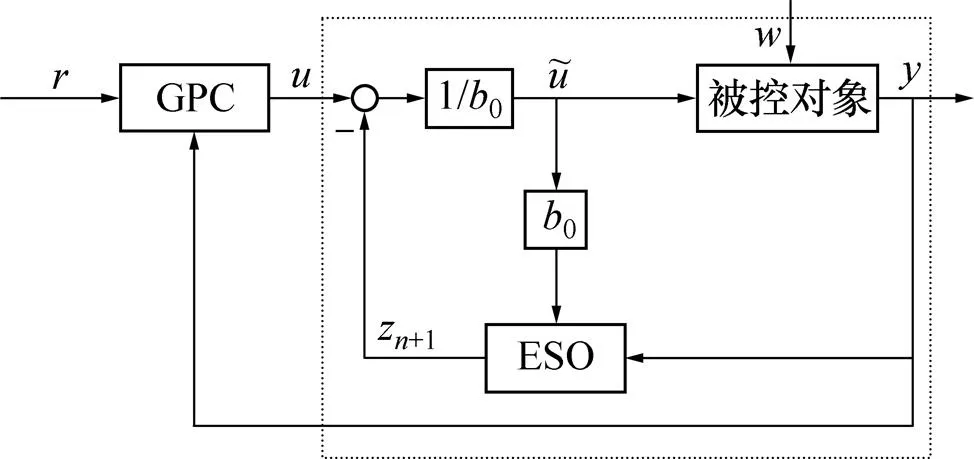
图1 ADRC−GPC结构

1.2 自抗扰广义预测控制的推导

二阶线性系统表达式如下：

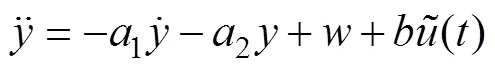
式中：为控制器的增益；1和2分别为系数；为连续时间变量。

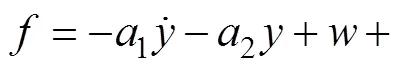
将式(2)写成状态空间的形式：

式中：1和2分别为系统输出及其一阶导数；3为总扰动或扩张状态。针对扩张后的系统(见式(3))，设计状态观测器即ESO，分别对1，2和3进行估计：

式中：1，2和3分别为不同扩张状态观测器的增益；1，2和3分别为状态1，2和3的估计值。由于实际输出1是可以直接测量的，通过减少对其的估计可以减少相位延迟,也就是说，式(4)中的ESO与降阶ESO相比，有一定的滞后性，尤其是对于时滞系统来说，会使得时滞对象的滞后加剧。因此，对于时滞系统，设计如下的降阶扩张状态观测器。将系统的状态方程即式(3)改写成如下形式：

构造如下降阶ESO表达式：

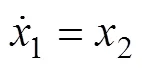
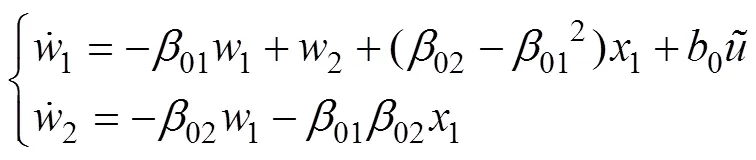
通过式(8)可分别得到降阶ESO的输出即1和2，继而可以分别求得2和3的估计值2和3。

设计如下控制律：

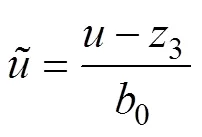
式中：为虚拟控制量，用来对简化后的系统施加控制作用。

在自抗扰广义预测控制算法中，广义预测控制器是对经过ESO估计和补偿后的积分器串联型系统施加控制作用，其从输入()到输出()之间的传递函数的表达式为

式中：a为多项式系数，=1，2，…，n；b为多项式系数，=1，2，…，n；c为多项式系数，=1，2，…，n。为简单起见，令(−1)=1。

CARIMA模型固有的积分作用有助于消除系统的静态偏差，但由于经ESO估计补偿后的被控对象本身就是积分器串联型控制系统，若采用CARIMA模型作为预测模型，则增加了积分环节。对于时滞系统，当观测器的带宽接近于0时才能实现稳态控制，因此，针对时滞系统，为了改善控制效果，以CARMA模型作为预测模型：

式中：为离散域上的采样时间。

对于二阶系统，在经过ESO估计和补偿之后，被控对象被简化成一个二阶积分器，其传递函数0()为

式中：为连续域的拉普拉斯算子。

采用零阶保持器得到积分器串联型系统的脉冲传递函数0(−1)：

式中：为变换算子，为采样周期。

忽略扰动信号，将式(13)改写成如下形式：

式中：1(−1)为脉冲传递函数，其表达式为

式(15)和式(17)相对应，由此可以得到

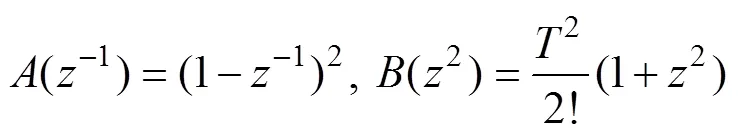
基于CARMA模型，考虑式(19)中的丢番图方程，则有

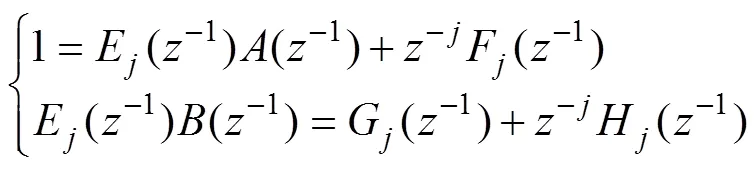
式中：=1，2，…，。E，F，G和H分别为关于−1的多项式：

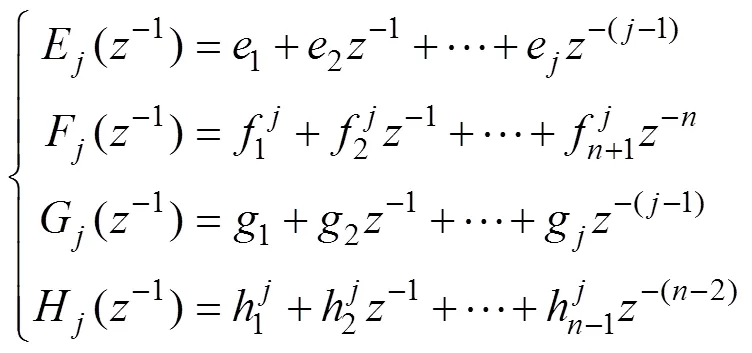
式中：e和g分别为对应的多项式系数，=1，2，…，；f为多项式系数，=1，2，…，＋1，h为多项式系数，=1，2，…，－1(其中=1，2，…，)。

当1时，H(−1)=0。将式(16)~(18)代入式(19)可以得到二阶系统丢番图方程的通解。

广义预测控制性能指标函数如下：

式中：()为对输出的预测序列；()为将来的控制序列；()为设定值的柔化序列；为控制时域；(＞0)为控制加权因子；()=0(，…，)，表示在u步后控制量不再变化。()的作用是使输出()可以平稳到达设定值()，其向量表达式如下：

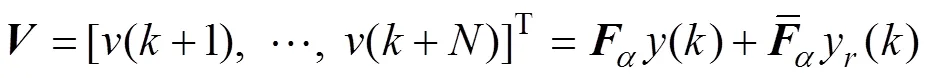
将式 (17)和(19)代入式(16)，可以得到步后系统的输出预测值()：

将式(23)写成向量形式，则有

其中：

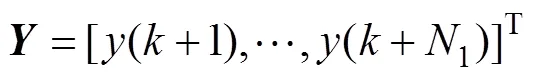
将式(21)写成向量形式，则有

将式(24)代入式(25)，可以求得使性能指标取得最小值时的控制律为

取的第1个元素作为控制量()。将()代入式(9)可以得到基于CARMA模型的二阶系统在自抗扰广义预测控制下的控制律。

1.3 自抗扰广义预测控制闭环离散形式

从上述分析中可以看出[11−12]：

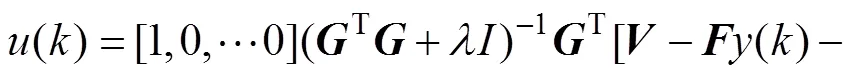
将式(22)代入式(27)可得：

即

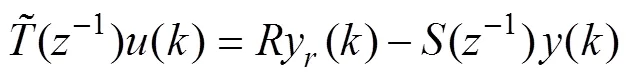
其中：

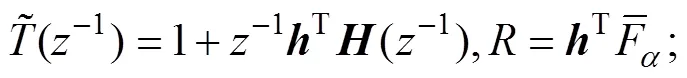
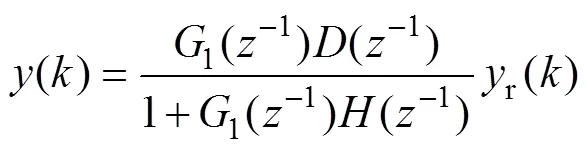
此时，GPC算法可以转化成闭环离散系统的形式，其广义预测控制下的闭环控制系统结构如图2 所示。

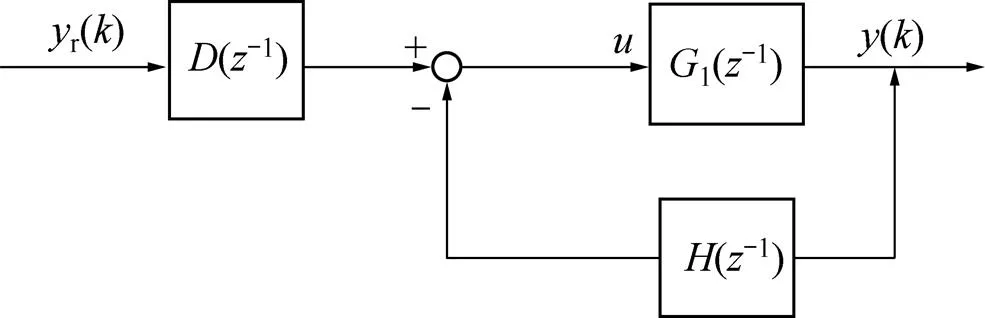
图2 广义预测控制下的系统闭环反馈结构

现对图1中虚线框内ESO和被控对象组合而成的回路部分进行简化，整理式(6)~(8)可得[13]

由此可以得到二阶时滞系统降阶ESO的内模控制的结构示意图如图3所示(其中为时滞)。

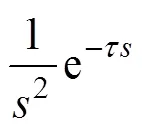
ADRC−GPC下的闭环离散系统的结构示意图如图4所示。

由图3可以求得到的传递函数：

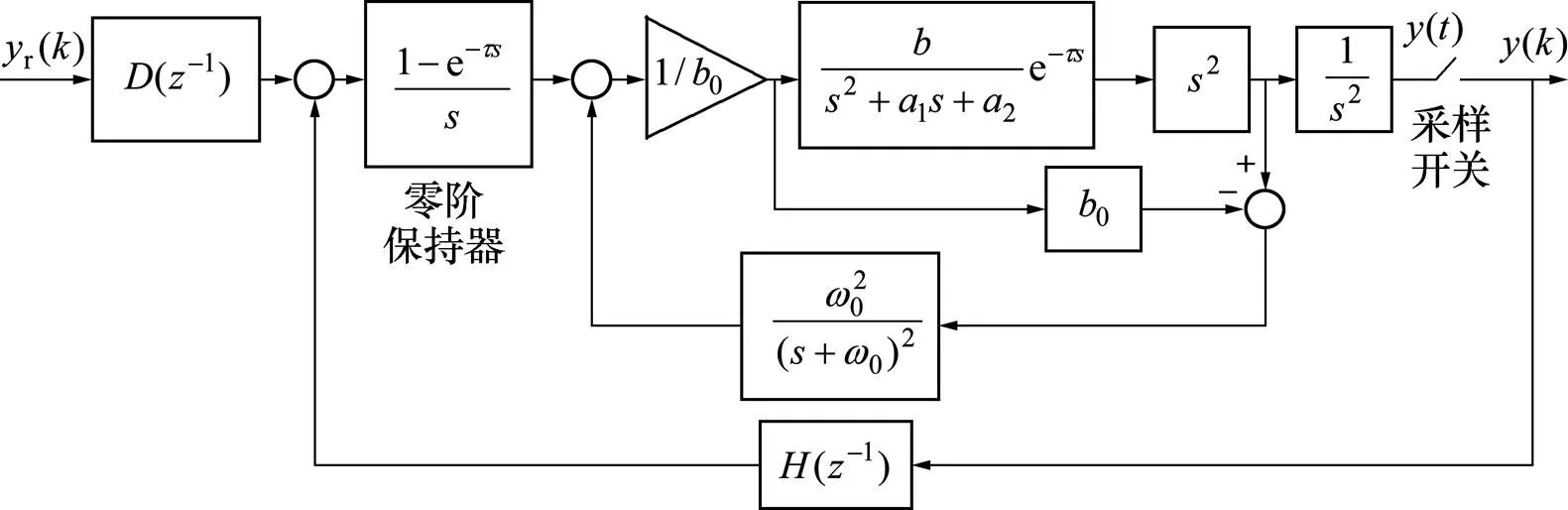
图4 自抗扰广义预测控制下系统的闭环反馈结构

将指数函数在零点处按二阶泰勒展开[14]，e−τs近似为

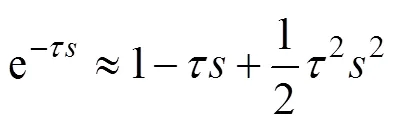
则闭环系统的特征方程变为

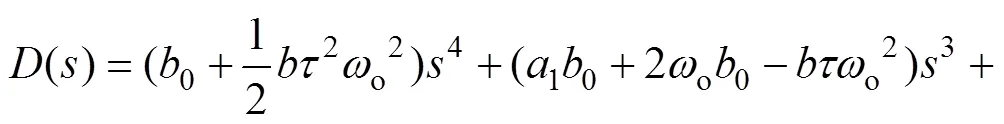
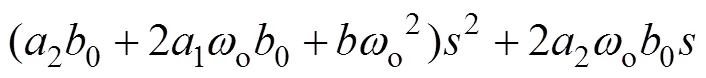
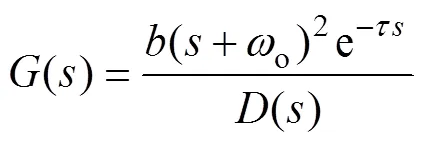
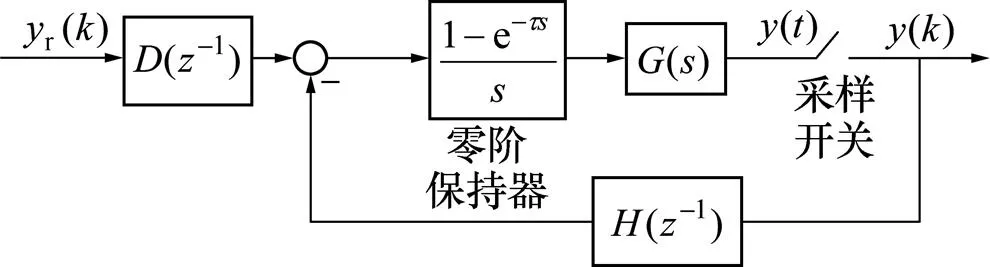
图5 自抗扰广义预测控制下系统简化闭环反馈结构

根据离散系统的稳定性条件，设

则图5中闭环系统的特征方程为

频域分析法是分析算法性能的常用方法，主要以Bode图或奈氏曲线为分析工具。与时域分析法相比，频域分析简单、直观，无需大量计算，通过系统的开环传递函数可以定性分析算法的性能。因此，为分析ADRC−GPC算法的性能，只需考虑(−1)(−1)的频率响应就可以，其表达式如下：

根据离散系统奈式判据，可得到在ADRC−GPC的控制下闭环系统稳定的条件。

2 ADRC−GPC的稳定性检测

设二阶时滞被控对象的传递函数为

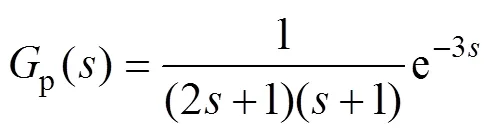
对于时滞系统，增大0能够提高时延系统的稳定性，实现期望的控制性能。因此，选择0=30，采样周期=0.1，o=10，根据式(35)和(36)，可以得到被控对象的离散化模型：

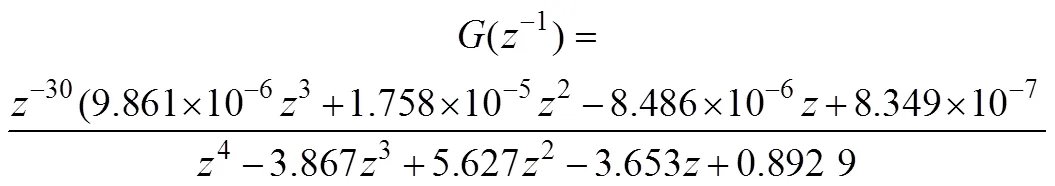
从上述分析可知：自抗扰广义预测控制的性能主要受到，o，，和N这5个参数的影响。下面分别对其进行调整，利用Bode图来观察参数变化对算法的性能的影响。

2.1 观测器带宽ωo对系统性能的影响

当o取值分别为2，5，10，15，20，25和30时，取=15，=1，=0.9，=0.5，0=35，采样周期=0.1。o变化时系统的Bode图如图6所示。图6所对应的截止频率和相角裕度如表1所示。

从图6可以看出：对于时滞系统来说，o增加对系统的响应速度和稳定性有很大影响。o越大，时滞系统的截止频率越高，系统的响应速度越快，但是系统的相角裕度减小，降低了系统的稳定性。由于ESO的估计精度与o有关，o越大，ESO估计精度越高，性能越好。但是，o增加使得系统的输入和输出对噪声更敏感。因此，o需要限制在合适的范围内，既能起到滤波的作用，又能保证一定的观测精度，从而获得满意的的控制效果。

(a) 幅值；(b) 相角

表1 ωo变化时系统的相角裕度和截止频率

2.2 预测时域N的改变对系统性能的影响

由于时滞的存在，的取值应该稍微大一些，因此从=15开始，当分别取值为15，20，25，30，35，40，45，50和55时，取=2，o=10，=0.1，0=30，=0.9，采样周期=0.1。系统的Bode图及其离散阶跃响应如图7所示。图7所对应的截止频率和相角裕度如表2所示。

从图7可以看出：预测时域改变会同时改变系统的截止频率和相角裕度。当较小时，系统截止频率较大，系统具有较快的响应速度，但是系统的相角裕度相对较小，稳定性相对较差，可能会产生较大的超调。当较大时，系统截止频率较小，使得系统的响应速度减慢，增加了计算时间，系统的实时性降低；但是系统的相角裕度较大，系统具有较高的稳定性。因此，在实际选择时应选择合适的，使控制系统既具有较快的响应速度，又能达到稳定性的要求。改变对算法快速性的影响可以从图7中的阶跃响应看出。

(a) 幅值；(b) 相角

表2 N变化时系统的相角裕度和截止频率

2.3 Nu改变对系统性能的影响

当u改变时，为更好观察其变化对于系统性能的影响，分以下2种情况考虑：≤0.5和≥0.5。取=25，o=5，=0.1，0=30，=0.9，此时系统的Bode图分别如图8和图9所示。图8和图9所示的Bode图所对应的截止频率和相角裕度如表3所示。

相对于其他参数来说，对于系统的稳定性和快速性影响较小。在广义预测控制中，由于优化的输出预测最多只受到个控制增量的影响，所以，应满足≤。从图8可以看出：越小，跟踪性能越差。为了改善跟踪性能，需要增加控制步长来提高对系统的控制能力。当＜0.5时，随着增大，系统的截止频率比=1时的截止频率小，即响应速度与=1时相比开始减慢，而系统的相角裕度比=1时的相角裕度大，系统的稳定性与=1时相比得到改善。而当≥0.5时，系统截止频率和相角裕度不会随着增大而发生改变。从式(24)可以看出，增大会使得矩阵的维数增加，算法在线计算量增加，使得算法的实时性降低，因此，在选择时，应该兼顾快速性和稳定性。

(a) 幅值；(b) 相角

(a) 幅值；(b) 相角

表3 Nu变化时系统的相角裕度和截止频率

2.4 控制加权常数λ的变化对系统性能的影响

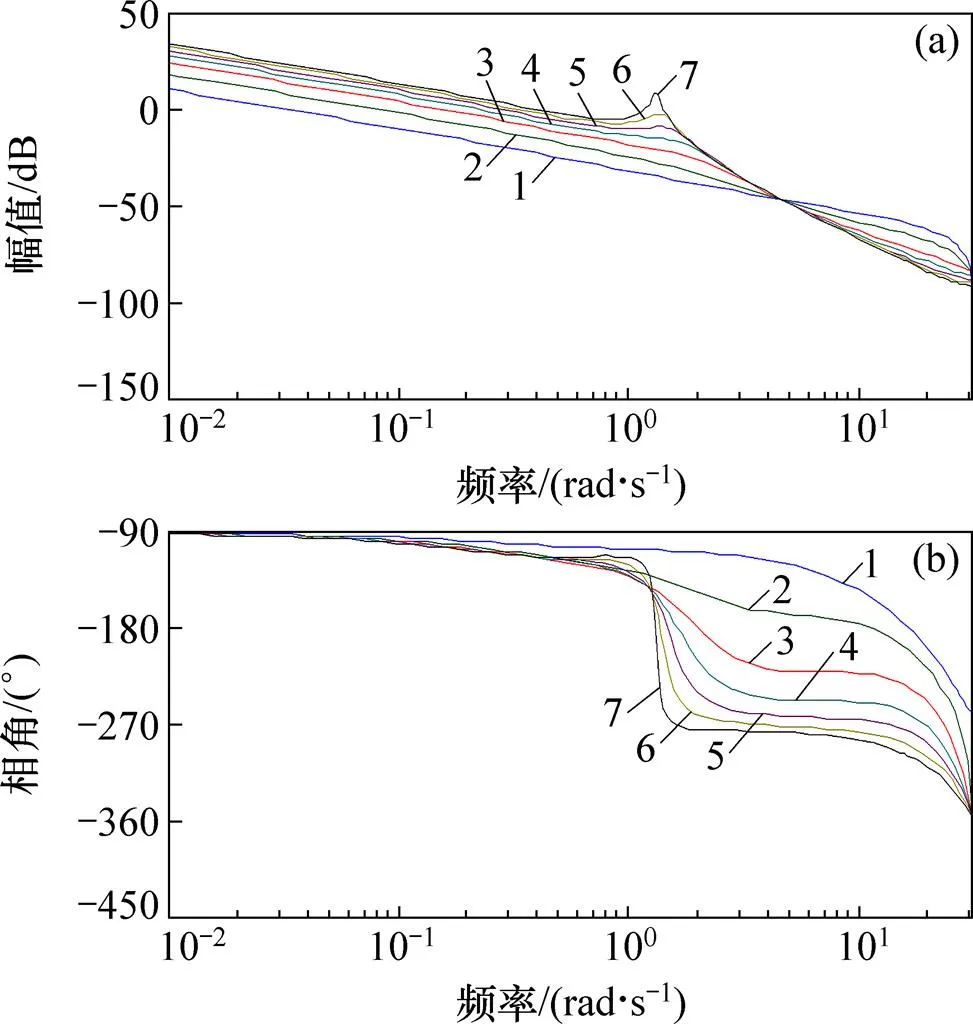
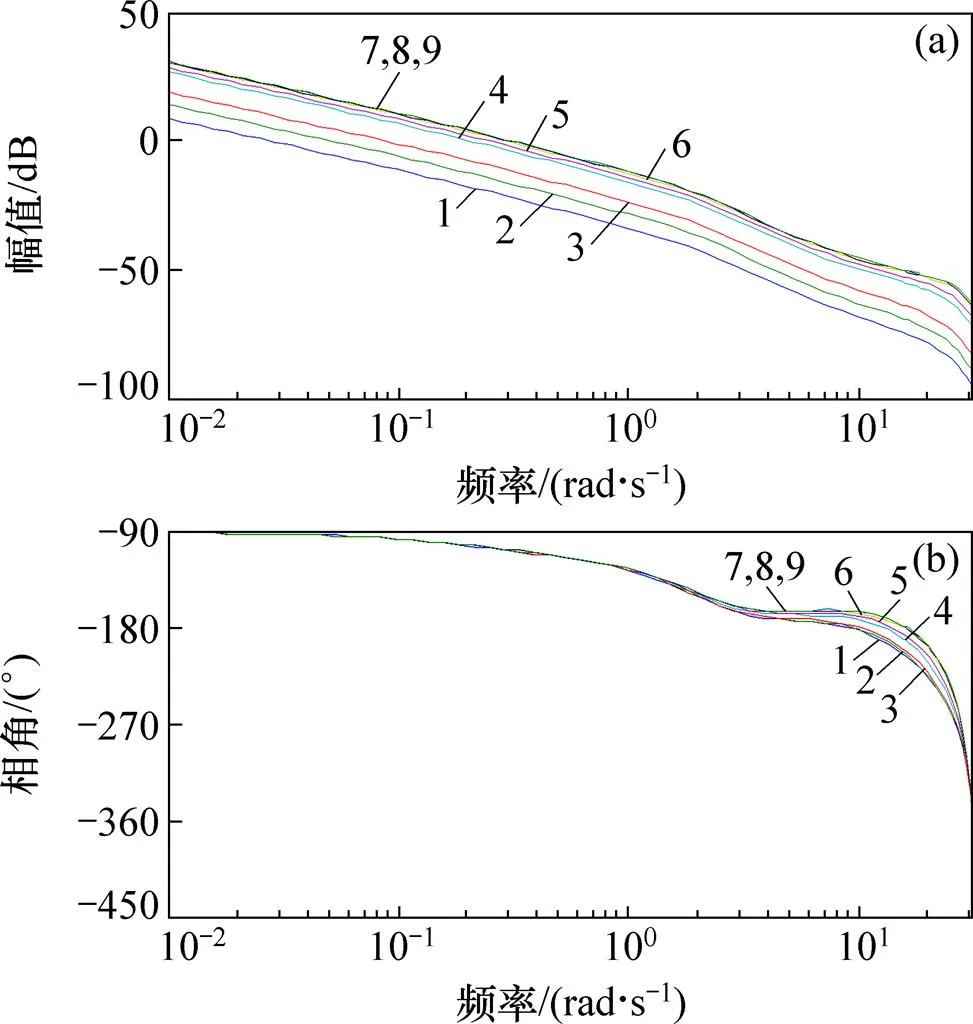
当取值分别为5.0，1.0，0.5，0.1，0.5×10−1，0.1×10−1，0.5×10−2，0.1×10−2，0时，取=15，o=5，=0.9，=1，0=30，采样周期=0.1。系统的Bode图如图10所示。图10所示的Bode图所对应的截止频率和相角裕度如表4所示。

是用来限制控制增量Δ的剧烈变化，以防止对被控对象造成过大冲击。从图10和表4可以看出：对系统的快速性和稳定性有很大影响；当很小时，减小对系统的截止频率和相角裕度几乎没有影响；而当较大时，增大会使得系统的截止频率逐渐降低，系统响应速度减慢，而系统相角裕度提高，系统的稳定性得到改善，可以实现稳定控制。但由式(26)可知增加会使得控制作用减弱，因此，实际选择时，应取一个合适的值，使得系统既能实现稳定控制，又具有较快的响应速度，且控制量的变化满足设计要求。

2.5 柔化因子α的变化对系统性能的影响

当取值分别为0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8和0.9时，取=15，o=5，=0.1，=1，0=30，采样周期=0.1。系统的Bode图如图11所示。图11所对应的截止频率和相角裕度如表5所示。

(0≤＜1)为柔化因子，可以使当前的输出()平稳到达设定值r()。增加降低了系统的截止频率，减缓了系统的响应速度，但使得系统的相角裕度增加，稳定性得到提高，系统超调量减小。从表5可以看出：当≤0.5时，随着增加，系统的截止频率和相角裕度基本不变；而当＞0.5时，随着越来越接近1，系统的截止频率和相角裕度的变化越来越明显，系统响应速度和超调量减小速率逐渐加快。因此，在实际进行参数选择时，若确定了预测时域的值，则为了保证闭环系统的稳定性，的选取应充分接近1。

(a) 幅值；(b) 相角

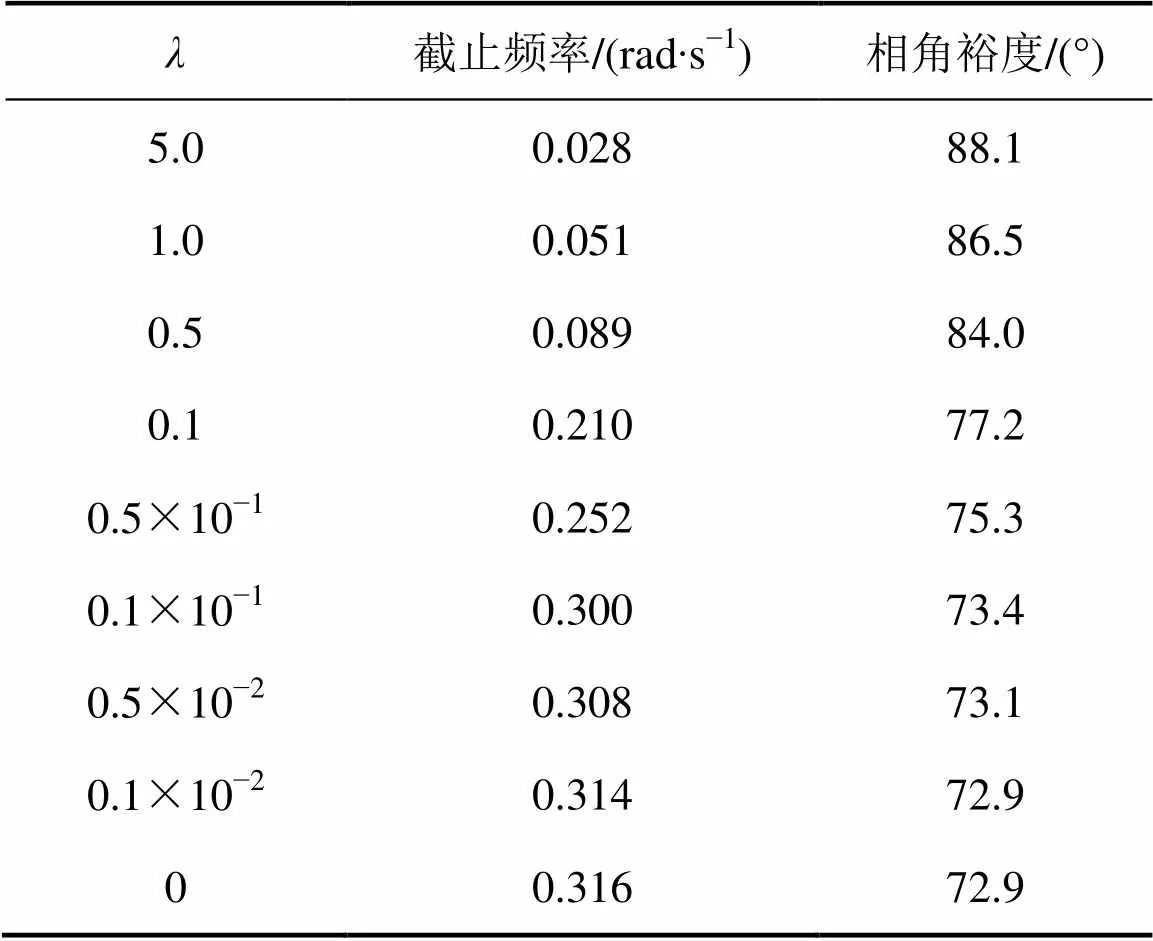
表4 λ变化时系统的相角裕度和截止频率

(a) 幅值；(b) 相角

：1—0.1；2—0.2；3—0.3；4—0.4；5—0.5；6—0.6；7—0.7；8—0.8；9—0.9。

图11变化时系统的Bode图

Fig. 11 Bode diagram of system whenchanges

表5 α变化时系统的相角裕度和截止频率

2.6 b0变化对系统性能的影响

对于时滞系统来说，当0=时，很难达到系统的稳定性要求，而增大0能够提高时滞系统稳定性。因此，当0取值分别为10，15，20，25，30，35和40时，取=15，o=5，=0.1，=3，=0.9，采样周期=0.1。系统的Bode图如图12所示。图12所对应的截止频率和相角裕度如表6所示。

对于时滞系统，可以看出0对系统的稳定性有很大影响。0增加明显降低了系统的截止频率，减缓了系统的响应速度，降低了系统的实时性。但0增加能够提高系统的相角裕度，改善系统的稳定性，使得系统实现期望的控制性能。因此，实际选择时应该综合考虑，应既能满足响应速度的要求，又能实现稳定控制。

(a) 幅值；(b) 相角

表6 b0变化时系统的相角裕度和截止频率

从上述分析可知，自抗扰广义预测控制器与广义预测控制器的参数调整原则基本一致，所不同的是，对于时滞系统来说，，0，，o和变化都会对ADRC−GPC算法的稳定性和快速性造成较大影响。在实际选取参数时，对于简单的时滞系统，N和取值比较固定，N选为1，而取近似于1，它们可以作为固定的参数无需调节，且当N选为1时，矩阵为列向量，算法的在线计算量减少，算法实时性提高。当控制系统稳态性能的要求较高时，N取值应该稍微大一些。的选取应该从0或者1个较小的数开始缓慢增加，直至获得满意的性能且控制律的变化满足设计要求。，0和o是ADRC−GPC算法中3个主要的可调参数。其中，0是根据来设计的，一般情况下，0相对于越大越好，但是0过大使得系统的调节时间过长，降低了算法的实时性。在实际选择时，可以先将0选定为1个相对来说较大的数，在获取满意的稳态性能后，可以缓慢减小0来获得满意的动态性能。的取值一般小于/，由于时滞的存在，不能过小，否则系统不能实现稳定控制，并且的取值应随着时滞增大而有所增加。在实际选择时，可以从一个相对于/来说较小的数开始调整，如果出现超调，缓慢增加；而且增大时，也应该相应增加，否则，较大的和较小的可能会影响系统的稳定性。而o的选取需要限制在一定范围内，在时滞系统中，o不能选取过大，否则系统会出现较大超调甚至发散。此外，o的选取需要保证ESO的估计精度。

2.7 仿真对比

为了实际比较GPC与ADRC-GPC这2种算法的动态性能，对式(39)中的系统施加阶跃响应，2种控制器的参数如表7所示。在仿真时间的1/2处，调节参数不变，对控制量施加给定值20%的阶跃扰动，系统的阶跃响应曲线如图13所示。

表7 2种控制器的参数

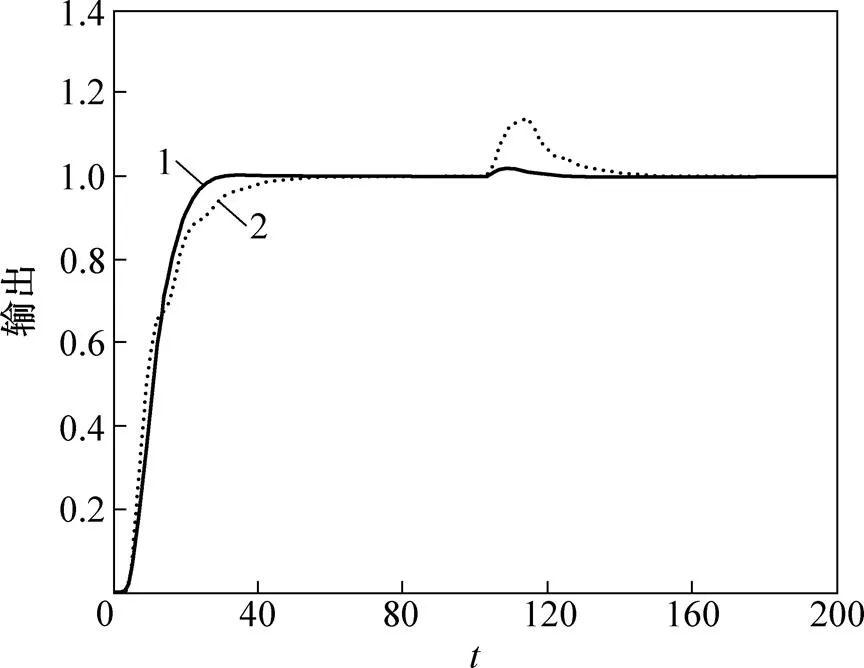
1—ADRC−GPC；2—GPC。

3 结论

1) 本文提出的自抗扰广义预测控制算法无需辨识被控对象的参数，避免了由于参数辨识不准确而影响算法性能的问题。该算法可以离线求得丢番图方程的解析解，与传统的广义预测控制算法相比，算法的实时性得到提高。

2) 得到自抗扰广义预测控制算法的闭环反馈结构。针对二阶时滞系统，研究了在ADRC−GPC的控制器作用下系统的频域特性，分析了控制器以及观测器的参数变化对系统性能的影响，获得控制器参数调整的原则与规律。

3) 通过比较在 ADRC−GPC以及GPC控制器作用下二阶时滞系统的动态响应，验证了ADRC-GPC算法相对于GPC算法的优越性。

[1] HAN Jingqing. From PID to active disturbance rejection control[J]. IEEE Trans on Industrial Electronics, 2009, 56(4): 900−906.

[2] 韩京清. 自抗扰控制技术—估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 183−287. HAN Jingqing. Active disturbance rejection control technique: the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008: 183−287.

[3] 韩京清. 抗扰控制器及其应用[J]. 制与决策, 98, 13(1): 19−23. HAN Jingqing. Active disturbance rejection controller and its applications[J]. Control and Decision, 1998, 13(1): 9−23.

[4] GAO Zhiqiang. Active disturbance rejection control: from an enduring idea to an emerging technology[C]//Proceedings of the 10th International Workshop on Robot Motion and Control. Poznan, Poland: IEEE, 2015: 269−282.

[5] 叶孝璐, 俞立, 张文安等. 基于串级ADRC的四旋翼飞行器悬停控制[J]. 中南大学学报(自然科学版), 2017, 48(8): 2079−2087. YE Xiaolu, YU Li, ZHANG Wenan, et al. Cascade ADRC-based hover control for quadrotor air vehicles[J]. Journal of Central South University(Science and Technology), 2017, 48(8): 2079−2087.

[6] 陈增强, 孙明玮, 杨瑞光. 线性自抗扰控制器的稳定性研究[J]. 自动化学报, 2013, 39(5): 574−580. CHEN Zengqiang, SUN Mingwei, YANG Ruiguang. On the stability of linear active disturbance rejection control[J]. Acta Automatica Sinica, 2013, 39(5): 574−580.

[7] HUANG Yi, XUE Wenchao. Active disturbance rejection control: methodology and theoretical analysis[J]. ISA Transaction, 2010, 53 (4): 6083−6090.

[8] CLARKE D W, MOHTADI C, TUFFS P S. Generalized predictive control: part 1 and part 2[J]. Automatica, 1987, 23(2): 137−160.

[9] 席裕庚. 预测控制[M]. 2版. 北京: 国防工业出版社, 2013: 1−23. XI Yugeng. Predictive control[M]. 2nd ed. Beijing: National Defense Industry Press, 2013: 1−23.

[10] 陈增强, 孙明玮, 袁著祉. 采样系统预测控制的设计与分析[J]. 控制理论与应用, 2002, 19(2): 268−270. CHEN Zengqiang, SUN Mingwei, YUAN Zhuzhi. Predictive control design and analysis for sampled-data systems[J]. Control Theory and Applications, 2002, 19(2): 268−270.

[11] 毛宗星, 陈增强, 孙青林, 等. 基于频域的广义预测控制的鲁棒性分析[J]. 华东理工大学学报(自然科学版), 2002, 28(S1): 15−19. MAO Zongxing, CHEN Zengqiang, SUN Qinglin, et al. Analyzing the robustness of generalized predictive control based on frequency domain[J]. Journal of East China University of Science and Technology (Science and Technology), 2002, 28(S1): 15−19.

[12] 毛宗星, 陈增强, 孙青林, 等. 基于频域的广义预测控制的稳定性分析[J]. 控制与决策, 2002, 11(6): 859−862. MAO Zongxing, CHEN Zengqiang, SUN Qinglin, et al. Stability analysis of generalized predictive control based on frequency domain[J]. Control and Decision, 2002, 11(6): 859−862.

[13] 徐琦, 孙明玮, 陈增强, 等. 内模控制框架下时延系统扩张状态观测器参数整定[J]. 控制理论与应用, 2013, 30(2): 1−5. XU Qi, SUN Mingwei, CHEN Zengqiang, et al. Extended state observer tuning for time-delay systems in the framework of internal model control[J]. Control Theory and Applications, 2013, 30 (2): 1−5.

[14] 杨瑞光. 线性自抗扰控制的若干问题研究[D]. 天津: 南开大学计算机与控制工程学院, 2011: 64−71. YANG Ruiguang. On linear active disturbance rejection control[D]. Tianjin: Nankai University. College of Computer and Control Engineering, 2011: 64−71.

(编辑 伍锦花)

Performance analysis of active disturbance rejection generalized predictive control on time-delay systems

CHEN Zengqiang1, 2, WU Xia1, SUN Mingwei1, SUN Qinglin1

(1. College of Computer and Control Engineering, Nankai University, Tianjin 300350, China; 2. Key Lab of Intelligent Robotics of Tianjin, Tianjin 300350, China)

In order to achieve high performance control of time-delay system, a new algorithm, i.e., active disturbance rejection generalized predictive control (ADRC-GPC) was proposed. First, the design process of the new algorithm was introduced. Then the closed-loop feedback structure of ADRC-GPC algorithm was deduced. Second, frequency domain analysis method was used to analyze frequency characteristics of ADRC-GPC method, and the parameters tuning principle of the algorithm was summarized. At last, dynamic performance of ADRC-GPC algorithm was compared with that of GPC algorithm. The results show that the proposed method can get the general solutions to Diophantine equations off-line and does not need to identify the system parameters, so the online calculation burden is reduced greatly. ADRC-GPC algorithm shows better dynamic performance than the traditional GPC control algorithm.

generalized predictive control; active disturbance rejection control; active disturbance rejection generalized predictive control; closed-loop feedback structure; frequency domain analysis methods

TP273

A

1672−7207(2018)08−1960−11

10.11817/j.issn.1672−7207.2018.08.017

2017−08−01；

2017−09−17

国家自然科学基金资助项目(61573199，61573197)(Projects(61573199, 61573197) supported by the National Natural Science Foundation of China)

陈增强，博士，教授，博士生导师，从事智能预测控制、工业过程控制等研究；E-mail：chenzq@nankai.edu.cn