面向电厂管道的攀爬机器人运动规划与仿真
2018-09-07寇重光谢涛陈潇游鹏辉肖晓晖
寇重光,谢涛,陈潇,游鹏辉,肖晓晖
面向电厂管道的攀爬机器人运动规划与仿真
寇重光,谢涛,陈潇,游鹏辉,肖晓晖
(武汉大学 动力与机械学院,湖北 武汉,430072)
针对电厂管道检测作业,围绕多屏平行管道环境中直管、管间和管屏间的攀爬作业需求,设计一种5自由度攀爬机器人,并进行运动规划分析。首先,分析运动需求,确定攀爬机器人的构型;其次,针对直管攀爬、管间过渡和管屏过渡的攀爬运动进行规划,提出3种步态;之后,采用基于D-H法建立的机器人运动学模型,采用逆运动学求解对应位姿点的关节角度;再通过5次多项式插值得到角度−时间序列;最后,采用ADAMS虚拟样机技术进行仿真,分析攀爬过程中的能耗及各关节的受力情况。研究结果表明:所规划的步态能够满足运动需求;直管攀爬中随着步距由50 mm增大至150 mm,机器人最大转矩增加17.76%,总能耗降低39.94%,在保证关节转矩足够的情况下可通过增大步距以降低能耗;各工况中,管间过渡的旋转关节与管屏过渡的夹持手爪所需力矩最大,在步态优化与样机设计时需重点校核。
管道攀爬机器人;运动规划;运动学;仿真分析
对在役管道进行定期维护对管道安全至关重要,目前多采用人工作业,其工作量大,效率低,危险性高。开发一种能够在管道环境中作业的攀爬机器人具有重要意义。在电厂多屏管道环境中,机器人沿直管攀爬、管间和管屏过渡的运动规划,是实现自主作业的关键。SPENKO等[1−2]研制的仿蟑螂机器人RiSE能够在地面和各种垂直建筑物表面攀爬;ZHANG等[3]研制了含主体、头部和尾部模块的仿毛虫攀爬机器人,研究了机器人在壁面上直行、转弯、旋转与滚动的运动能力;LAM等[4−5]研制的Treebot能够以蠕动的方式在含分支机构的树木上爬行。YOON等[6]研制的三自由度桁架攀爬机器人Shady 3D,能够在细长方形截面杆构成的三维桁架内移动,但攀爬位姿严重受限;TAVAKOLI等[7−8]研制的四自由度3D Climber串行夹持攀爬机器人能够克服弯头、T型连接、法兰和圆杆的直径变化;HAN等[9−10]研制了一种遥控管道外攀爬机器人,通过2个攀爬驱动模块和1个运动连接臂的协调运动进行攀爬,可越过法兰、阀体、弯头等障碍。以上机器人的攀爬对象为单一杆件,不能实现电厂环境中2根管道之间的过渡。曹志华等[11]研制了五自由度电力铁塔攀爬机器人,通过电磁吸附实现沿电力铁塔角钢攀爬、越障和转向;江励等[12−14]研制了模块化构型的五自由度仿尺蠖攀爬机器人Climbot,可以满足更多的运动需求;KIM等[15−16]研制了一种基于视觉的爬杆机器人,采用五自由度构型,通过图像处理与激光传感器辅助机器人进行自主抓夹;吴伟国等[17]针对空间桁架结构设计了双臂手移动机器人,采用六自由度串联机构在桁架内移动。以上4种机器人已实现基本攀爬功能,但没有具体应用于电厂管道,尚未对管间、管屏过渡进行深入研究。基于此,本文作者针对电厂的多屏管道,设计1种管道攀爬机器人。首先分析运动需求,确定机器人构型;然后进行运动规划与运动学分析,提出直管攀爬、管间过渡、管屏过渡3种步态;最后进行虚拟样机仿真,分析比较不同工况下的关节力矩与能耗,为运动规划的优化以及样机设计提供依据。
1 运动需求分析与构型设计
1.1 运动需求分析
电厂环境中的管道主要为多屏平行排管,如图1所示。图1中:Ⅰ与Ⅱ表示两屏平行管道,管屏距为1;①与②表示同一屏管道中的相邻管道,管间距为2。应用于其中的攀爬机器人应具备沿竖直管的攀爬、同屏管道中相邻管的管间过渡以及相邻管屏间的管屏过渡等运动能力。
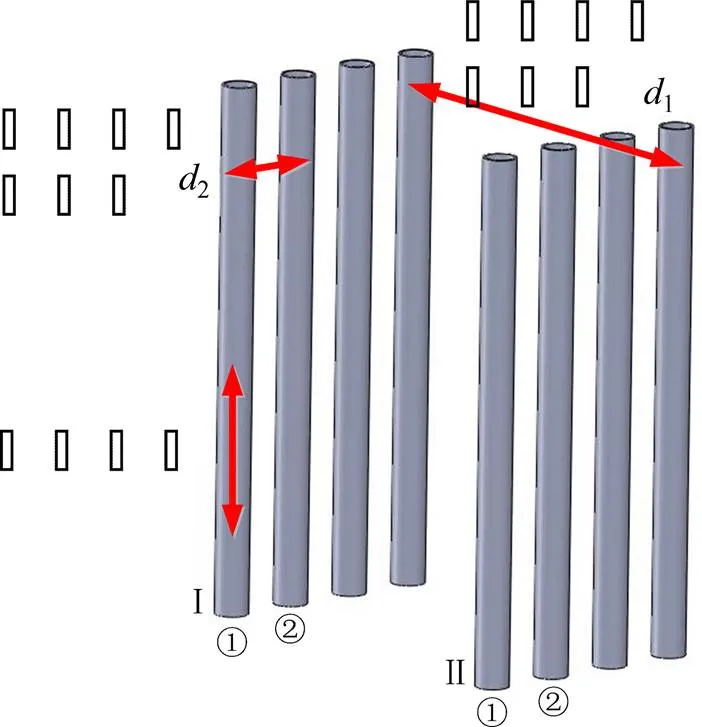
图1 电厂管道模型
1.2 机器人构型设计
机器人在三维空间内攀爬至少需要4个自由度,但过渡攀爬时攀爬位姿受到严格限制,无法满足任务需求;六自由度机器人能够实现三维空间攀爬的任意位姿[18],但其控制难度较大。
考虑本文所研究的作业对象中多屏管道平行的特点,拟减少1个自由度,采用五自由度构型。所设计的机器人机构简图与三维模型如图2所示,其中a~e这5个旋转自由度关节依次串联构成机器人本体,夹持手爪S1和S2安装在首尾两端。机器人一端夹持时,通过5个旋转关节配合,末端手爪可沿,和轴移动,也可绕和轴旋转,满足多屏管道环境的工作需求。

(a) 机构简图;(b) 三维模型
2 运动规划
机器人采用一端手爪固定,另一端手爪移动,两手爪交替夹持的方式进行攀爬。根据电厂管道环境的要求,提出3种攀爬步态。
2.1 直管攀爬步态
直管攀爬是机器人攀爬的基本步态,拟定1个步距的攀爬步态,如图3所示。
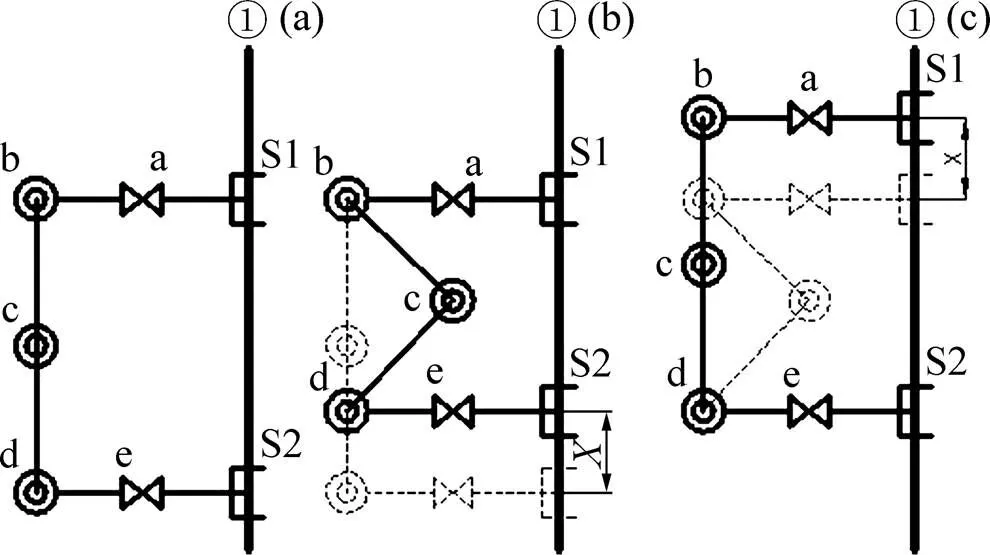
(a) 初始姿态;(b) “M”型姿态;(c) 结束姿态
图3(a)中,机器人两手爪均抓紧管道,处于初始位置。
图3(b) 中,手爪S2张开,S1仍保持夹紧,单独支撑机器人。旋转关节b,c和d协调转动,机器人本体收缩呈“M”型姿态,使手爪S2前进1个步距。
图3(c)中,手爪S2夹紧管道,S1张开,转换为手爪S1支撑机器人。旋转关节b,c和d反向协调转动,机器人本体伸展,恢复至初始姿态,手爪S1夹紧管道。至此,机器人前进1个步距。
2.2 管间过渡步态
机器人完成1根管道的攀爬后,需要过渡到同一屏管道中相邻管继续作业,拟定管间过渡步态如图4所示。
图4(a)~(b) 中,手爪S1夹紧管道①,支撑机器人。手爪S2张开,旋转关节c和d协调转动,将手爪S2抬起一定高度离开管道①,为机器人管间过渡作准备。

(a) 初始姿态;(b) 准备姿态;(c) 过渡姿态1; (d) 过渡姿态2;(e) 过渡姿态3;(f) 结束姿态
图4(b)~(c)中,旋转关节a转动,整个机器人绕关节a旋转,进行管间跨越。手爪S2运动至管道②的位置后,关节c和d反向协调转动,放下手爪S2,对管道②进行夹持。
图4(d)中,手爪S2夹紧管道②,支撑机器人。手爪S1张开,抬起离开管道①。
图4(d)和(e)与图4(b)和(c)类似,旋转关节e转动,整个机器人绕关节e旋转,进行管间跨越,手爪S1运动至管道②位置,机器人恢复初始姿态。
图4(f) 中,手爪S1夹紧管道②。至此,完成由管道①向②的管间过渡。
2.3 管屏过渡步态
管屏过渡是机器人第2种过渡攀爬步态,拟定步态如图5所示。
图5(a)~(b)中,手爪S1夹紧管道Ⅰ,支撑机器人。手爪S2张开,将手爪S2抬起一定高度离开管道Ⅰ,为机器人管屏过渡做准备。
图5 (c)中,旋转关节b,c和d协调转动,将手爪S2移动到预定位置。此时,c和d之间的连接横梁平行于管道,关节e垂直于管道。
图5(d)中,通过关节b,c和d协调转动,在保证关节e与管道垂直的同时,调整手爪S2位置使其对准管道Ⅱ。随后,手爪S2夹紧管道Ⅱ,至此,管屏过渡完成第1阶段。
图5 (e)与图5(b)类似,手爪S1松开,并抬起一定高度。手爪S2夹紧管道Ⅱ支撑机器人。
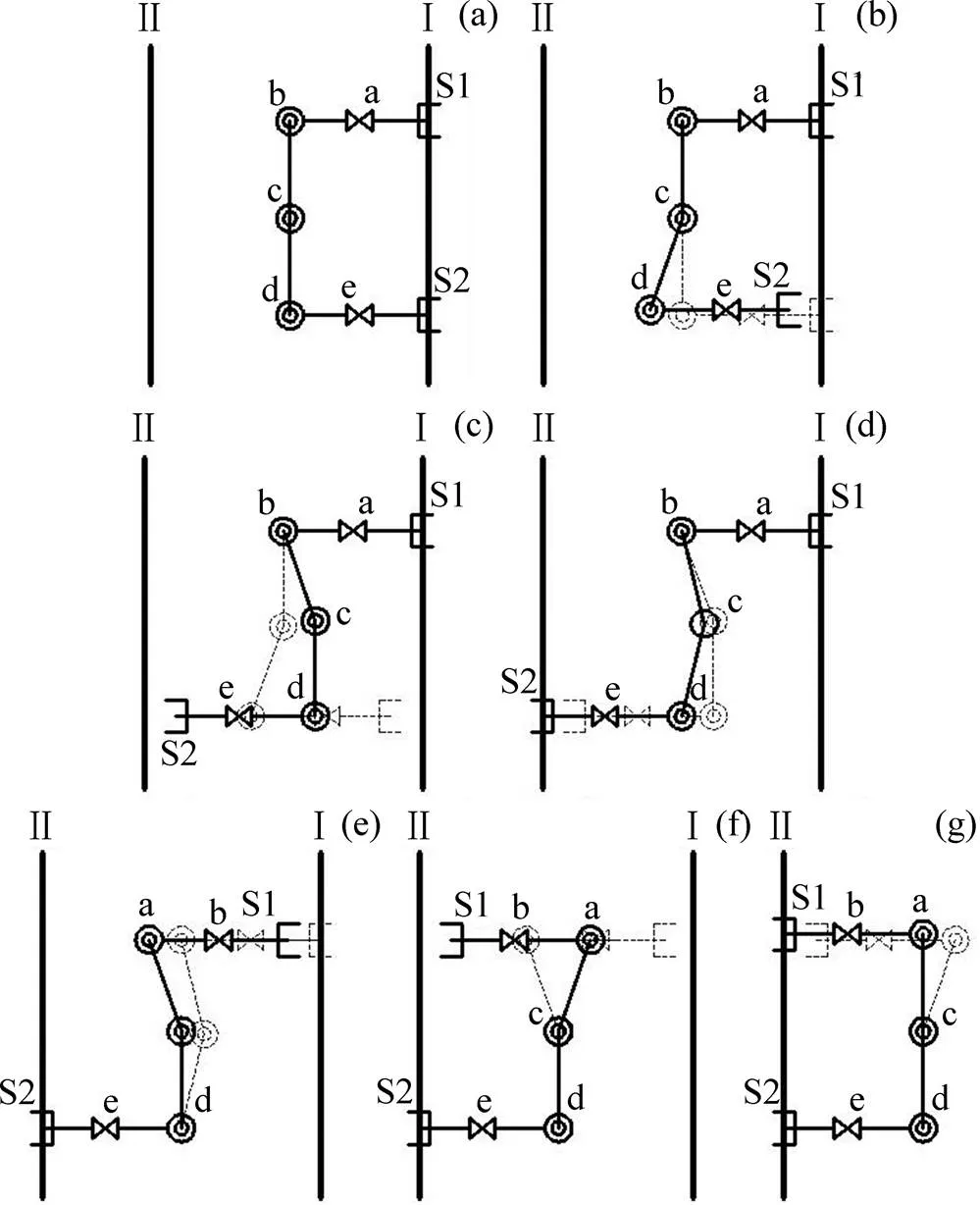
(a) 初始姿态;(b) 准备姿态;(c) 过渡姿态1;(d) 过渡姿态2;(e) 过渡姿态3;(f) 过渡姿态4;(g) 结束姿态
图5(f)和(g)与图5(c)和(d)类似,通过关节b,c和d协调转动,将手爪S1移动至预定位置,此时,c和d间横梁平行于管道,关节b垂直于管道。再调整手爪S1位置,使其对准管道Ⅱ,同时机器人恢复初始姿态,手爪S1夹紧管道Ⅱ。至此,完成由管屏Ⅰ向管屏Ⅱ的过渡。
3 运动学分析
机器人运动学反映各个关节与末端执行器间的运动关系,包括机器人的运动学建模和逆运动学求解。解出各关节变量后,插值求得机器人各关节运动角度−时间序列。
3.1 机器人运动学模型
管道攀爬机器人运动学模型如图6所示。基于修正D−H法[18−19],机器人上端的夹持手爪S1固定时,以其夹持中心为参考坐标系原点0,在各关节轴线上取原点1~5,依次建立坐标系{0}~{5}。机器人D−H参数如表1所示。
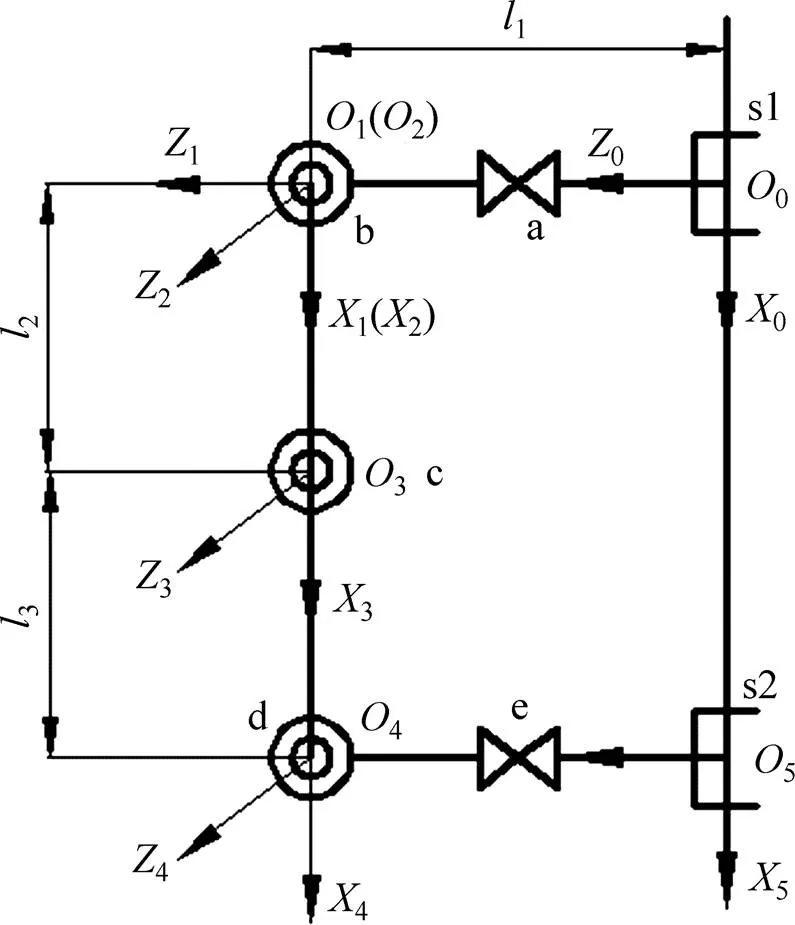
图6 管道攀爬机器人运动学模型
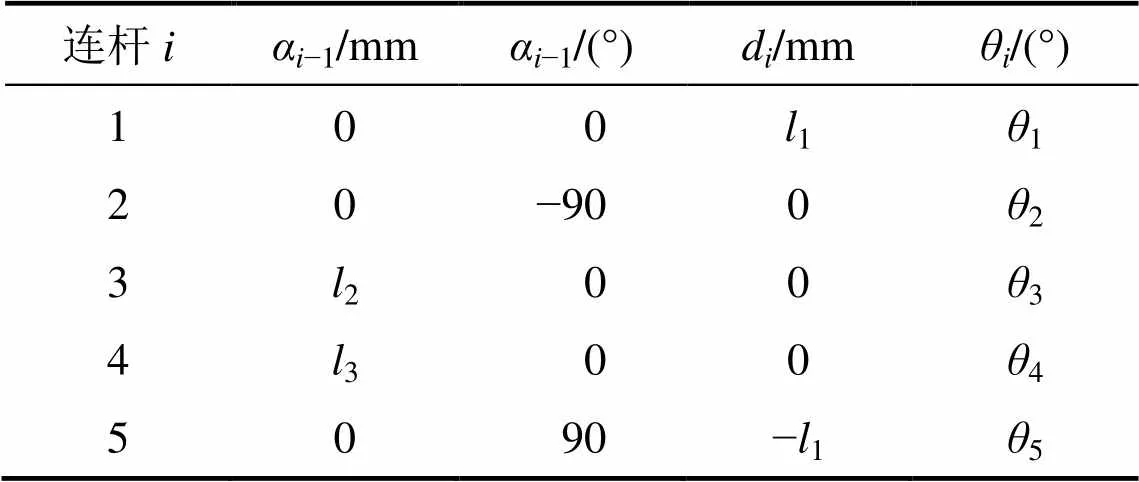
表1 机器人D-H参数
注:−1为绕X−1轴从Z−1旋转到Z的角度;d为沿Z轴从X−1移动到X的距离;为绕Z轴从X−1旋转到X的 角度。
3.2 运动学方程
机器人末端夹持手爪S2的坐标系相对于固定端S1处参考坐标系的位姿转换矩阵为
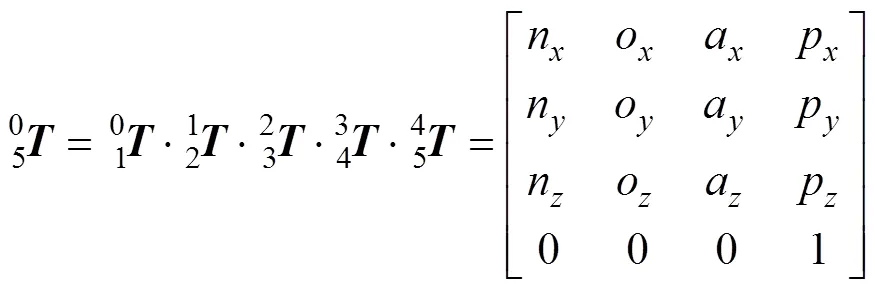
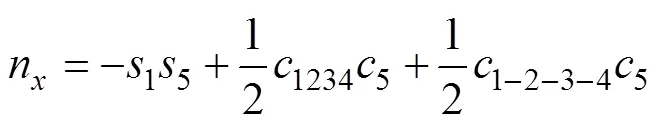


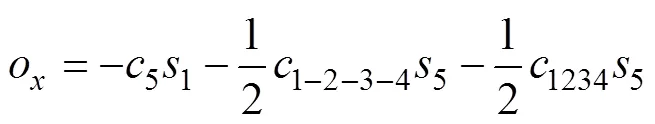

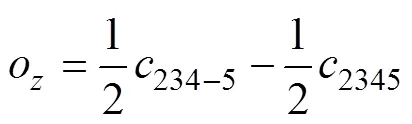
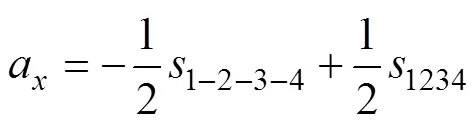

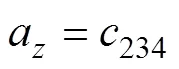
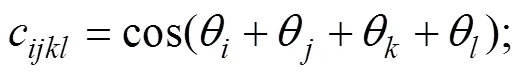
,,和均取1,2,3,4和5,下同。
3.3 逆运动学求解

或


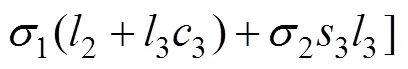

或

由式(2)~(6)得:
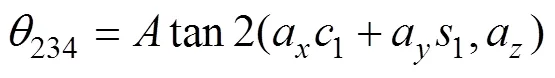
或
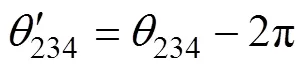


或
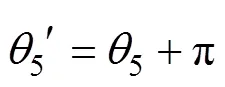
其逆解存在多解,综合考虑机器人结构限制、位姿和工作空间等因素确定最优解,得到各关节所需运动角度。
3.4 关节轨迹插值
为保证机器人运动平稳、无冲击,要求在所设计的攀爬步态须经过的关键路径点处各关节的速度、加速度为零。采用5次多项式函数对各路径点的关节角度进行插值,

约束条件:

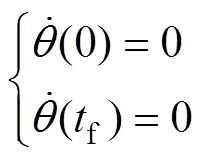
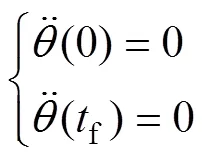
式中:C为常量;f为运行时间;0为前一路径点关节角度;f为后一路径点关节角度。
求解C得到5次多项式为
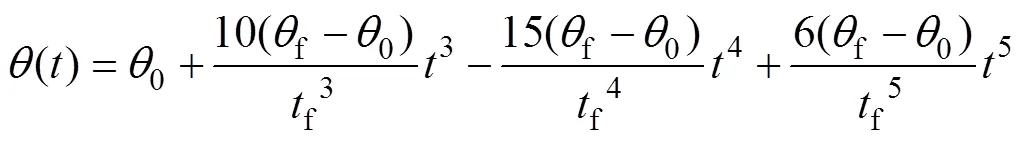
4 攀爬仿真分析
本机器人以电厂多屏平行管道为作业对象。图1中管道尺寸参数为:管屏距1=600 mm,管间距2= 200 mm。图6中机器人尺寸为:1=260 mm,2=3=180 mm。所设计的机器人各模块参数如表2所示。
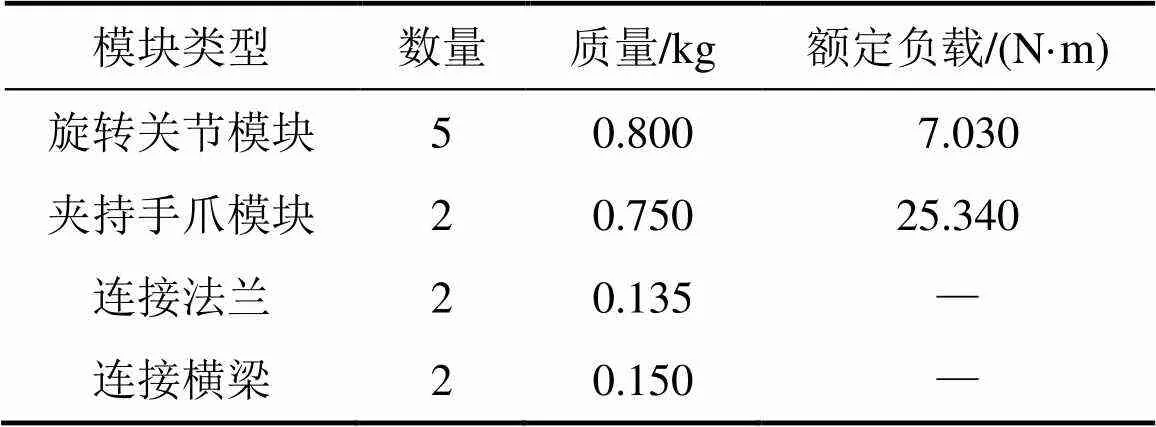
表2 机器人模块参数
在ADAMS环境中建立虚拟样机模型如图7所示。通过对不同工况进行仿真,验证机器人的运动能力,比较分析攀爬能耗以及各关节的受力情况。
4.1 直管攀爬仿真与分析
根据2.1节中规划的步态进行攀爬仿真。直管攀爬过程中,只需b,c和d这3个关节联合运动,其中b与d这2个关节结构对称,受力情况近似。150 mm步距时,b和c这2个关节的力矩时程曲线如图8 所示。
分析图8可知:1) 旋转关节力矩存在3处异常突变,分别在开始运动时刻、7.5 s两手抓交替夹持时刻、运动结束时刻。这是由于仿真模型中各零件全部设置为刚性接触,而以上时刻2只手爪同时夹持,造成过约束,使得关节力矩突变。在实际工作过程中,由于机构存在一定间隙与弹性,将不会发生这种情况;2) 在0.6~7.3 s,机器人逐渐收缩成“M”型姿态,旋转关节b为主要承力关节,关节力矩随机器人姿态变化逐渐增大,至7.3 s达到最大值4.31 N·m;3) 两手爪在7.6 s交替夹持后,关节b转变为从动关节,关节力矩减小。
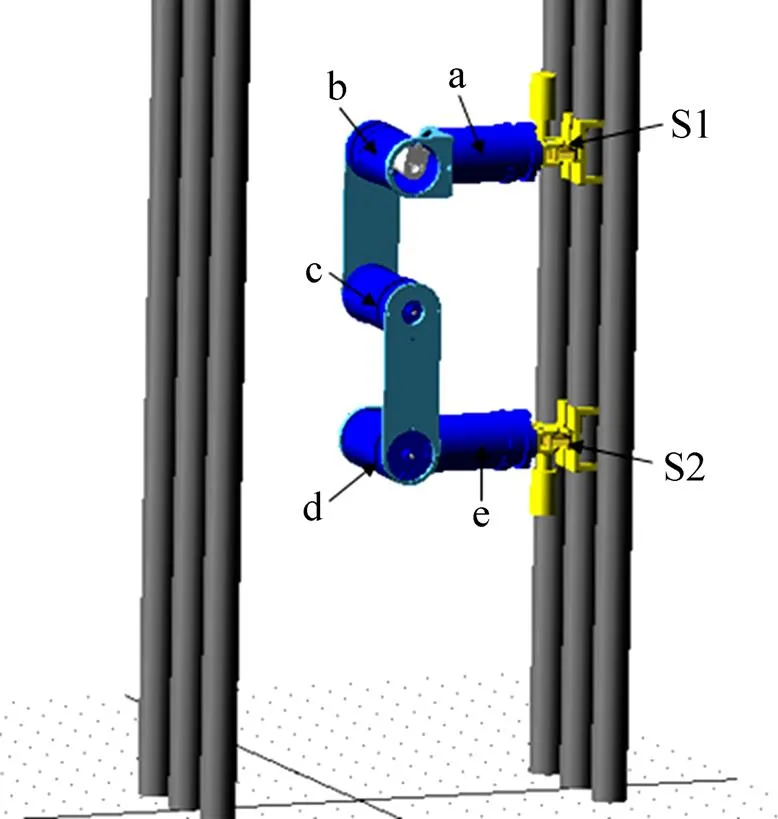
图7 机器人虚拟样机模型
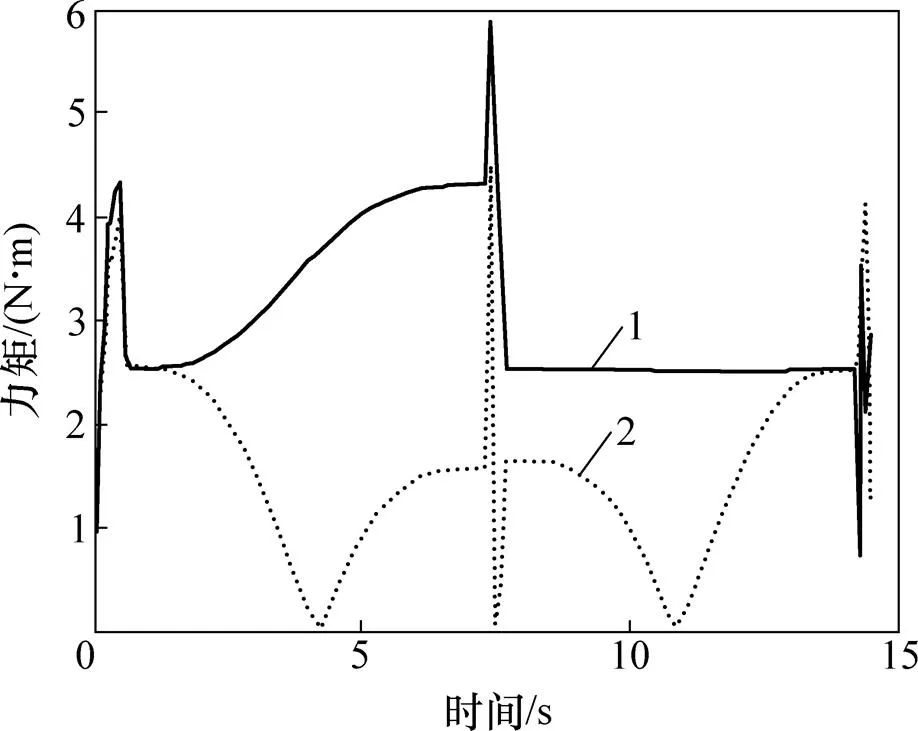
旋转关节:1—b;2—c。
取50,75,100,125和150 mm这5种攀爬步距,以相同的速度攀爬1 500 mm进行仿真。机器人关节力矩及能量消耗有所不同,其最大关节力矩及总能耗见表3。
由表3可知:随着攀爬步距增大,机器人最大关节转矩增大,能量消耗降低。当步距由50 mm增大至150 mm时,机器人最大转矩增加17.76%,总能耗降低39.94%。在关节电机负载允许的条件下应增大步距,以节省能量。
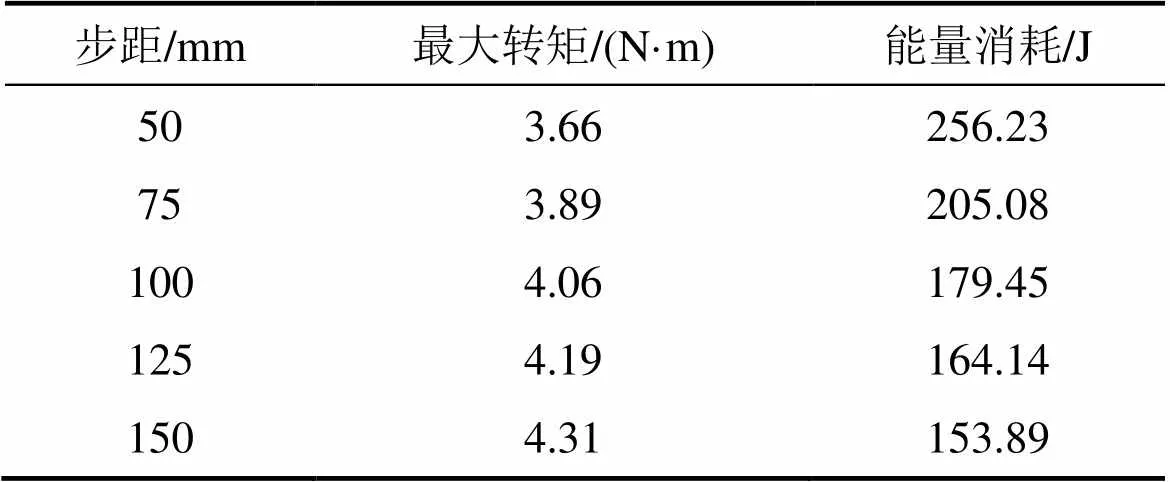
表3 以不同步距攀爬时关节转矩及能耗
4.2 过渡攀爬仿真与分析
根据2.2节与2.3节中规划的步态,进行管间过渡与管屏过渡攀爬仿真,用时均为29 s。管间过渡需5个关节联合运动,由于结构对称性,取a,b和c这3个关节进行分析,其力矩时程曲线如图9所示。管屏过渡取b和c这2个关节进行分析,其力矩时程曲线如图10所示。
分析图9和图10可知:
1) 与直管攀爬类似,管间过渡与管屏过渡运动中,除2只手爪同时夹持的3个时刻旋转关节力矩存在异常突变外,机器人整体上运动平稳。
2) 在管间过渡攀爬过程中,在6.4~10.1 s时,机器人一端夹持,旋转关节a带动机器人向目标管道移动,是主要承力关节,其关节力矩随着机器人的旋转逐渐增大;在10.1 s运动至目标位置后,达到最大值6.71 N·m。
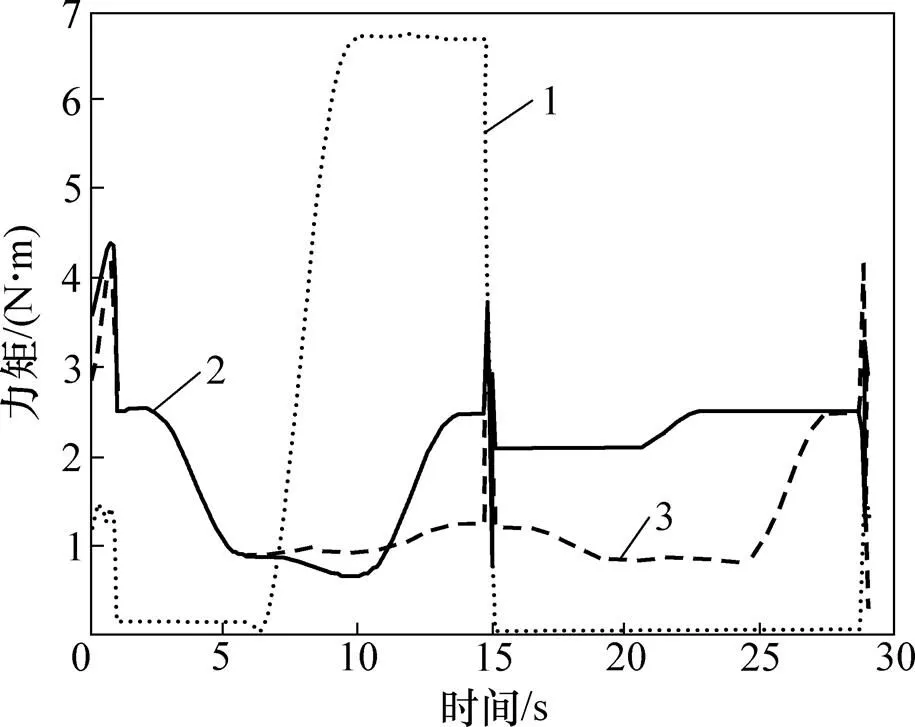
旋转关节:1—a;2—b;3—c。
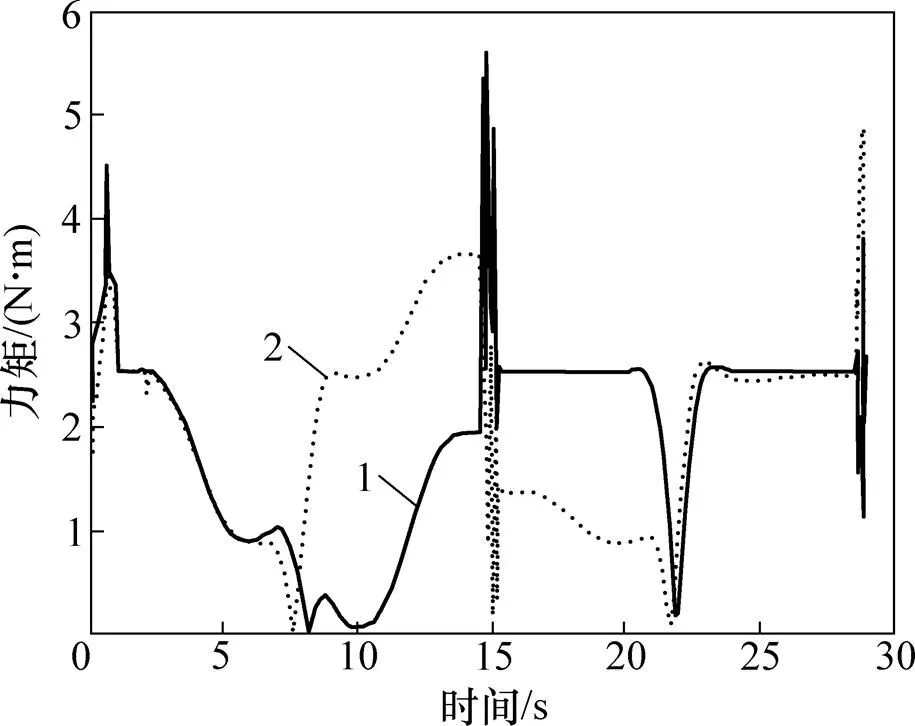
旋转关节:1—b;2—c。
3) 管屏过渡攀爬过程中,旋转关节c是主要承力关节,其关节力矩在14.7 s手爪S2运动至目标管道夹持时达到最大值3.99 N·m。
4.3 不同工况下各模块关节力矩对比
在攀爬运动过程中,手爪的夹持性能对机器人的安全运行至关重要。以管屏过渡为例,其手爪力矩时程曲线如图11所示。
由图11分析:手爪夹持管道的瞬间存在冲击碰撞,力矩达到极值,随后趋于平稳;受重力影响,下端手爪S2夹持时所需驱动力矩更大,在15.2 s达到最大值22.11 N·m。

夹持手爪:1—S1;2—S2。
不同工况下各模块关节力矩如表4所示。从表4可以看出:机器人动作幅度越大,关节力矩越大;在旋转关节中,管间过渡过程中a关节所需力矩最大,为6.71 N·m;夹持手爪中,管屏过渡过程所需手爪力矩最大,为22.11 N·m。各关节最大力矩均小于电机额定负载(见表2),验证了机器人的攀爬能力。

表4 不同工况下各模块关节力矩
5 结论
1) 针对电厂的多屏管道环境设计了1种管道攀爬机器人,根据任务需求提出直管攀爬、管间过渡、管屏过渡这3种步态,并通过运动学理论规划出各关节的角度−时间序列。
2) 通过ADAMS软件进行虚拟样机仿真。仿真结果表明:机器人能实现所规划的运动;直管攀爬应增大步距以节省能量;各工况中,管间过渡的旋转关节与管屏过渡的夹持手爪负载最大,对步态优化与样机设计具有指导意义。
[1] SPENKO M J, HAYNES G C, SAUNDERS J A, et al. Biologically inspired climbing with a hexapedal robot[J]. Journal of Field Robotics, 2008, 25(4/5): 223−242.
[2] AUTUMN K, BUEHLER M, CUTKOSKY M, et al. Robotics in scansorial environments[C]//Proceedings of SPIE: the International Society for Optical Engineering. Orlando, USA: SPIE, 2005: 291−302.
[3] ZHANG Houxiang, WANG Wei, GONZÁLEZ-GÓMEZ J, et al. Design and realization of a novel modular climbing caterpillar using low-frequency vibrating passive suckers[J]. Advanced Robotics, 2009, 23(7/8): 889−906.
[4] LAM T L, XU Y. A flexible tree climbing robot: Treebot-design and implementation[C]//Proceedings: IEEE International Conference on Robotics and Automation.Shanghai, China: IEEE, 2011: 5849−5854.
[5] LAM T L, XU Y. Climbing strategy for a flexible tree climbing robot−treebot[J]. IEEE Transactions on Robotics, 2011, 27(6): 1107−1117.
[6] YOON Y, RUS D. Shady 3D: a robot that climbs 3D trusses[C]//Proceedings: IEEE International Conference on Robotics and Automation. Rome, Italy: IEEE, 2007: 4071−4076.
[7] TAVAKOLI M, MARQUES L. 3DCLIMBER: climbing and manipulation over 3D structures[J]. Mechatronics, 2011, 21(1): 48−62.
[8] TAVAKOLI M, MARJOVI A, MARQUES L, et al. 3DCLIMBER: a climbing robot for inspection of 3D human made structures[C]//2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS. Nice, France: IEEE, 2008: 4130−4135.
[9] HAN S C, AN J, MOON H. A remotely controlled out-pipe climbing robot[C]//2013 10th International Conference on Ubiquitous Robots and Ambient Intelligence, URAI 2013. Jeju, Korea: IEEE, 2013: 126.
[10] HAN S, AHN J, MOON H. Remotely controlled prehensile locomotion of a two-module 3D pipe-climbing robot[J]. Journal of Mechanical Science and Technology, 2016, 30(4): 1875−1882.
[11] 曹志华, 陆小龙, 赵世平, 等. 电力铁塔攀爬机器人的步态分析[J]. 西安交通大学学报, 2011, 45(8): 67−72. CAO Zhihua, LU Xiaolong, ZHAO Shiping, et al. Gait analysis for electricity pylon climbing robot[J]. Journal of Xi’an Jiaotong University, 2011, 45(8): 67−72.
[12] 江励.双手爪式模块化仿生攀爬机器人的研究[D]. 广州: 华南理工大学机械与汽车工程学院, 2012: 17−48. JIANG Li. Development and analysis of a bio-inspired modular biped climbing robot[D]. Guangzhou: South China University of Technology. School of Mechanical & Automotive Engineering, 2012: 17−48.
[13] 朱海飞, 管贻生, 蔡传武, 等.具有多种运动方式的小型模块化双手爪机器人MiniBibot[J]. 机器人, 2012, 34(2): 176−181, 189. ZHU Haifei, GUAN Yisheng, CAI Chuanwu, et al. Minibibot: a miniature modular biped robot with multi-locomotion modes[J]. Robot, 2012, 34(2): 176−181, 189.
[14] 吴文强. 可重构模块化机器人建模、优化与控制[D]. 广州: 华南理工大学机械与汽车工程学院, 2013: 17−32. WU Wenqiang. Modeling.Optimation and control of reconfigurable modular robot[D]. Guangzhou: South China University of Technology. School of Mechanical & Automotive Engineering, 2013: 17−32.
[15] KIM J H, LEE J C, CHOI Y R. Vision-based pipe grasping scheme for a pole climbing robot[C]//2012 International Symposium on Optomechatronic Technologies, ISOT. Paris, France: IEEE, 2012: 6403252.
[16] KIM J H, LEE J C, CHOI Y R, et al. Automatic grasping of a pole climbing robot using a visual camera with laser line beams[C]//The 3rd International Conference on Control, Mechatronics and Automation, ICCMA. Barcelona, Spain: EDP Sciences, 2016: 03005.
[17] 吴伟国, 徐峰琳. 空间桁架用双臂手移动机器人设计与仿真分析[J]. 机械设计与制造, 2007(3): 110−112. WU Weiguo, XU Fenglin. Design and simulation analysis of a dual arm & hands mobile robot used in space truss[J]. Machinery Design & Manufacture, 2007(3): 110−112.
[18] 熊有伦, 丁汉, 刘恩沧. 机器人学[M]. 4版. 北京: 机械工业出版社, 1993: 20−48. XIONG Youlun, DING Han, LIU Encang. Robotics[M]. 4th ed. Beijing: China Machine Press, 1993: 20−48.
[19] 王润. 串联机器人运动学分析、结构优化设计及仿真研究[D]. 天津: 天津大学机械学院, 2012: 11−20. WANG Run. Research on the kinematics analysis, structural optimization design and simulation of serial robot[D]. Tianjin: Tianjin University. School of Mechanical Engineering, 2012: 11−20.
(编辑 陈灿华)
Motion planning and simulation of climbing robot for power plant pipeline
KOU Chongguang, XIE Tao, CHEN Xiao, YOU Penghui, XIAO Xiaohui
(School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)
To meet the kinematic demands of climbing task along a straight pipe, between pipes or between calandria pipelines in a multipanel paralleled pipelines environment, a 5-DOF climbing robot was analyzed and developed for power plant detection. Firstly, based on the motion demand analysis, the climbing robot structure configuration was designed. Secondly, climbing motions along a straight pipe between pipes and between calandria pipelines were planned, and three kinds of gaits were proposed. Afterwards, the kinematical model was established by using the Denavit−Hartenberg method and inverse kinematics was used to solve the corresponding position joint angle. Then angle-time series were obtained by quintic polynomial interpolation method. Finally, energy consumption and the torque of joints during the climbing process were analyzed by virtual prototyping simulation based on ADAMS. The results show that the planned gait can meet the needs of movement. With the increase of step distance from 50 mm to 150 mm in the straight pipe climbing, the maximum torque of the robot increases by 17.76% and the total energy consumption reduces by 39.94%,energy can be saved by increasing step in case of sufficient torque. In each condition, the load of rotating joints in climbing between pipes and clamping claw in the climbing between pipe screen are the maximun, and they should be checked in gait optimization and prototype design.
pipeline climbing robot; motion planning; kinematics; simulation analysis
TP242.2
A
1672−7207(2018)08−1936−08
2017−08−10;
2017−10−12
国家自然科学基金资助项目(51675385)(Project(51675385) supported by the National Natural Science Foundation of China)
肖晓晖,博士,教授,从事特种机器人与微操作机器人研究;E-mail:xhxiao@whu.edu.cn
10.11817/j.issn.1672−7207.2018.08.014
