缺失数据情形下概率密度函数的统计应用研究

张 亚,安佰玲

1.滁州城市职业学院基础部，滁州，239000;2.淮北师范大学数学科学学院,淮北,235000

1 相关研究与问题提出

概率密度函数是概率统计概念，主要用于计算数据密度大小[1]。一般情况下，设求解数据总体X对应的求解密度函数为f(x)，在总体数据X中抽取样本数据记为x1,x2,…,xn，根据给定的样本完成概率密度函数f(x)计算[2]。 目前，对于该函数的求解方法有很多种，应用较多的方法有最近邻密度估计法、正交序列估计法、核估计法和直方图估计法等[3]。

各个领域在应用该函数时，异常现象越来越频繁，主要表现为数据缺失[4]。为了避免数据缺失情况对概率统计结果造成影响，我国在此方面投入了大量资金，并设置了相关自然科学基金项目[5]。目前，国内学者对于缺失数据情形下概率密度函数的研究成果较少[6]。国外学者在此方面的研究成果更多，对于协变量有缺失的情况，利用参数模型，提出了概率密度函数估计方法[7]。除此之外，针对响应变量缺失情况，提出逆概率权法与校正法，充分分析了概率密度函数渐进性质，并对函数进行了估计计算[8]。在缺失数据情况下，极少有文献考虑经验似然置信区间问题，并作出数值试验。

2 数据缺失机制概述

从缺失机制与方式角度，可以将缺失数据样本归为以下三种类型。

(1)随机缺失样本：是一种依赖完全变量的数据样本。

(2)完全随机缺失样本：要求数据缺失既与完全变量无关，又与不完全变量无关。

(3)非随机缺失样本：该样本相比上述两种样本要繁琐一些，通常情况下，区分该样本采用的方法为排除法，如果数据样本不满足上述两种样本要求，则认为其为非随机缺失样本[9]。

目前，处理缺失数据的方法主要有两种，分别是完全记录单位法和填补法，前者包括删除法和加权调整法，后者包括单一填补法和多重填补法[10]。

3 缺失数据情形下的概率密度函数统计应用研究

3.1 非参数回归填补法

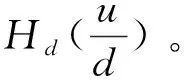
(1)完整样本数据情形。

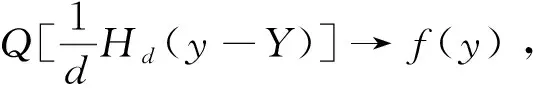
(2)缺失样本数据情形。

当函数集{Yj}出现数据缺失情况时，需要立即调整数据，然而在调整数据的过程中发现，在MAR假设条件下，

在上述公式中,U(x,y)=Q[Hd(y-Y|X=x)]，因此，使用非参数回归填补法求解函数f(y)的估计计算公式为：

3.2 逆概率权方法

该方法的估计计算方案如下：

首先，在满足X=x条件下，给定Y不缺失概率，用λ(x)表示，即λ(x)=P(σ=1|X=x)，并且将其记为λ(xj)=λj,1≤j≤m，

(1)当λj为已知量时，在MAR假设条件下

由上述公式可以得到逆概率权填补法的估算公式为

(2)一般情况下，λj未知，在估计计算时，可以使用以下方法对函数λ(x)进行估算：

在上述公式中，{Wmi(x):1≤i≤m}属于一组完全依赖函数集{x,Xj:1≤j≤m}的非负权函数。

4 缺失数据情形概率密度函数统计应用与分析

4.1 应用方案

为了探究本文提出的两种估算方案是否可行，将提出的估算方法应用到实际求解中，验证方案的可行性，最终达到解决缺失数据情形概率密度函数统计问题。

对非参数回归填补估计方案，通过分析构造函数f(y)经验似然置信区间，完成方案验证。采用同样的应用思路，探究逆概率权填补渐进置信区间。

在MAR 缺失机制下，设置如下数据缺失情形：

λ1(x)=P(σ=1|X=x)

={1+exp(-0.5x)}-1

针对上述情形，生成不完全样本数量5 000，表示形式为{xi,Yi,σi,i=1,2,…,m}，其中m取值260,200,140，同时取定区间1-α=0.95。使用上述不完全数据样本，采用逆概率权填补法和非参数回归填补法对样本函数的经验似然置信区间覆盖概率(CP)进行计算，同时求取平均区间长度(AL)。

4.2 应用结果与分析

按照上述应用方案执行，得到的结果真值在置信区间右方比率记为U，左方比率记为L，得到的结果见表1-3。

表1-3中的数据表明：(1)对于平均区间长度,采用非参数回归填补法得到的置信区间长度值更大一些；(2)当样本容量逐渐增加时，CP逐渐增加，最终达到0.95，在此期间，区间长度值有所减小；(3)接近名义覆盖水平的覆盖率获取方法为逆概率权填补法。

表1 f(0.6)不同样本容量m下的两种方法的AL与CP结果统计表

表2 f(0.8)不同样本容量m下的两种方法的AL与CP结果统计表

表3 f(1)不同样本容量m下的两种方法的AL与CP结果统计表

5 结 语

本文对缺失数据情形概率密度函数统计应用进行研究。研究依据概率密度函数理论和数据缺失机制理论，制定缺失数据情形概率密度函数估计方法，包括非参数回归填补法和逆概率权方法。通过分析实际应用结果可知，使用非参数回归填补法可以得到较大的置信区间平均长度值，而逆概率权填补法的应用结果更加接近名义覆盖水平覆盖率，CP随着样本容量的增加而变大，逐渐接近0.95。