铁电体的光伏效应∗

蔡田怡 雎胜

(苏州大学物理科学与技术学院,苏州 215006)

(2018年5月18日收到;2018年6月13日收到修改稿)

1 引 言

在现代经济迅速发展的驱动下,世界各国对能源的需求与日俱增,已成为世界经济可持续快速发展所面临的重大难题.在这一形势下,推进能源生产和消费革命,构建清洁低碳、安全高效的能源体系已成为我国近期的重要发展目标之一.开发和利用清洁、可再生的太阳能是解决问题和实现目标的重要思路.太阳能光伏电池的研究和设计也因此吸引了众多国内外研究者的广泛关注,其原理是利用光伏效应将太阳的光能转换为电能[1].目前,基于无机或有机半导体材料的光伏电池已经得到大量的研究,其中硅型光伏电池开发最早[2]、技术也最为成熟,已得到规模化生产,但其光电转换机制决定其转换效率不能突破Shockley-Queisser极限[3].虽然近来提出可以通过电池叠装等复杂的制造工艺提高光电转换效率,但毫无疑问造价不菲[4−6].因此,寻找新型的光伏材料以研制性能更优良、功能更丰富的太阳能电池已成为目前这一领域的研究热点.

40年前,Fridkin[7]提出可以利用铁电体实现光电能量转换,他甚至指出基于所谓的“光铁电晶体”能够制备太阳能电池.但在后来的研究工作中,以铁电体为基础的光伏器件研究大多仅仅局限于纯粹的学术领域,工业上的实际应用受到低量子效率以及低导电能力的限制.在理论上,铁电性的起源也并不清晰,直到现代铁电极化理论的建立[8],这一问题才得到明确的认识.近年来,很多令人兴奋的突破性成果在铁电体中被发现[9,10],包括高于能隙的光生电压、低能隙铁电体的发现和高光电转换效率,激发了众多研究者对铁电体光伏器件的研究热情.

需要注意的是,电子有电荷、晶格和自旋等多个自由度,自由度间相互作用、相互耦合,使铁电极化强度的量值和方向容易受到物理、化学和力学等多种外加手段的调控,使铁电体具有丰富的功能性和非比寻常的应用前景.例如,铁电体已经被用于制备记忆存储介质[11,12]、铁电场效应管和铁电随机存储器[13,14]等.铁电性和力学参量的耦合使铁电体还被设计应用于多种传感器中.最为重要的是,在一类“特殊”铁电体即多铁性材料中,还存在着活跃的磁性序参量,它与铁电序参量间存在着耦合作用,从而表现出丰富的磁电效应[15−18],例如,锰氧化物中的庞磁电阻、铁磁性和电荷序的共存以及巨磁介电效应等.这使多铁性材料从出现伊始就得到自旋电子学、磁电子学和光电子学等多个领域研究者的广泛关注[19−22].

本文以传统半导体中的光伏效应为出发点,介绍铁电体光伏效应的主要机制,包括体光伏效应和反常光伏效应,讨论铁电体在太阳能电池中的可能应用,探索增强光伏效应的方法,为铁电光伏效应引入新的自由度和新的调控手段.

2 传统光伏效应

当半导体吸收高于本征能隙能量的光子时,价带顶的电子将被激发跃迁至导带,产生电子和空穴载流子.这些被激发的载流子将很快衰减至基态,并通过发射光子或声子保持能量守恒.但是,当半导体中的静电势具有不对称结构(内建电场)时,可能将电子载流子和空穴载流子分离,向相反方向运动,从而出现光生净电子流或空穴流,即光电流.显然,光伏效应依赖于两个基本过程:首先是光生载流子的产生,这可以通过半导体吸收光实现;其次是在内建电场下光生电子和空穴被分离和收集,形成向特定方向流动的净电流.当人们认识到半导体对光的吸收能力后,后者成为设计制造太阳能电池的关键.

在太阳能电池的早期实验中,研究者曾在两个不同金属电极间插入硒薄层,形成肖特基势垒结构,不同金属电极间的功函数差异使金属-半导体接触界面附近的静电势不再对称,导致整流效应的出现.在1950年左右,研究者又设计出另一种结构以分离光生电荷.通过在硅薄膜的两端区域分别掺杂磷元素和硼元素,形成p-n结.如图1(a)所示,p-n结中的内建电场使光激发的电子空穴对被迅速分离,导致更为显著的光伏效应[23].传统光伏器件中,内建电场通常是依靠光伏器件结构中材料之间的显著差别在界面及其附近实现的,如p-n同质结、p-n异质结(例如CdS/CdTe薄膜电池)以及p-i-n结等.

图1 产生光伏效应的示意图[23] (a)半导体p-n结;(b)铁电光伏效应Fig.1.The photoelectric ef f ect in(a)the semiconductor p-n junction and(b)the ferroelectrics[23].

通过与理想光伏器件功率进行对比,可以容易地得到光电转换效率(power conversion efficiency,PCE)的一般定义.若入射光的功率为Pin,则光电能量转换效率η正比于开路电压Voc,短路电流Jsc和填充因子FF表示为

如图2所示,开路电压Voc和短路电流Jsc分别是光伏器件在理想条件下光生电压和光电流的最大值,理想太阳能电池产生的功率可以表示二者的乘积Pmax.由于载流子间的复合不可避免地带来能量的损失,实际器件在J-V曲线上所能得到的最大功率总是低于理想功率,它们的比值被称为填充因子(FF).显然,为了得到高光电转换效率的光伏器件,不仅要求具备良好的可见光吸收率和量子效率(输出电流),同时要求足够强的内建电场(输出电压).在传统的半导体光伏器件中,半导体对太阳光谱的吸收能力决定Jsc值的大小,而Voc的值受半导体的能隙所限制.另一方面,被光激发的热载流子通过非弹性散射弛豫至导带底,这一过程中能量的损失必然会导致PCE的降低.另外,为了得到较高的光电流,传统的半导体p-n结光伏器件对半导体/金属界面和制备薄膜技术均要求较高.

图2 太阳能电池的短路电流Jsc、开路电压Voc和理想功率Pmax[24]Fig.2.Schematic of solar cell output current as a function of voltage,for a shift current solar cell,displaying the linear relationship between current and voltage.Also shown are short-circuit current Jscand open-circuit voltage Vocpoints,and maximum power point,Pmax[24].

3 铁电光伏效应

为了突破光生电压的这一限制,研究者开始寻找产生内建电场的新机制,铁电体因为其具有高自发铁电极化强度而进入研究者的视野.研究者猜测铁电体中的铁电极化可以扮演“内建电场”的角色,迅速分离光生载流子向不同方向运动,并且这一相对较强的电场还将有效地降低载流子间的复合率,提高光电转换效率(图1(b))[23].实验上也证实,利用铁电体制备的太阳能电池可以得到较高的开路电压(Voc),并不受材料的本征能隙限制,在这一点上,明显优于p-n结半导体光伏器件.

目前,对铁电光伏材料和器件的研究包含以下独立的方向.随着单原子层可控的现代沉积技术的发展和现代铁电极化理论的建立,研究者试图从基础物理和材料设计的角度,探讨铁电氧化物中光伏效应的机制,寻找提高光电转换效率的新途径,BiFeO3成为这一方向上最受青睐的研究对象[25−29];受到发现高光电转换效率的鼓舞,越来越多的研究者将目光投向有机-无机杂化卤化物钙钛矿材料[30−36],尤其是CH3NH3PbI3,这无疑引领着太阳能研究领域新的发展趋势;还有些研究者进一步挖掘铁电光伏器件潜在的多功能性,在铁电体中,新的自由度(自旋自由度)被引入,光伏效应可被电场、磁场等多种外加手段所调控.

3.1 铁电光伏效应的唯象理论[37]

在短路条件下,光照使无对称中心的均匀介质产生稳态光电流jpv,并且jpv的值与光的极化相关.在开路条件下,这一结构可作为电流源,产生光电压,

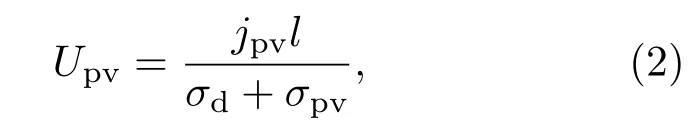
其中σd和σpv分别是暗电导和光电导,l是电极之间的距离.当σpv≫σd时,光伏效应产生的光生电场可以简化为

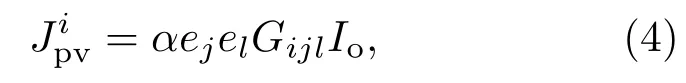
光电流的张量性质可以用下式表示:式中,ej和el是描述光极化的矢量分量;Gijl是三阶压电张量,G=el0ζφ(~ω)−1,其中参数ζ用来描述激发的反对称性.简单地,可以得到如下的标量关系:

单位面积铁电体的光电转换效率可以被定义为负载消耗的功率QR和吸收光的功率Qpv的比值,其中而因此,

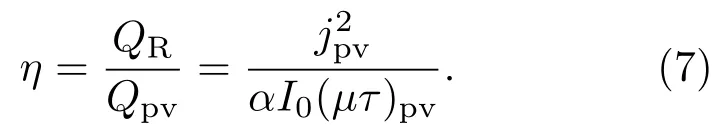
考虑到(5)式,光电转换效率进一步简化为η=GEpv.目前,实验上已经对大部分常见铁电体和压电体的G和Epv进行测量[38,39].以BaTiO3块材(C4v对称性)为例,实验发现G31∼ (3—6)× 10−9cm/V,Ep∼ 102V/cm,可以估计η∼10−7[38,40],显然这是个极低的值.但是,当铁电晶体的厚度减小到纳米尺度,即l与基态载流子的位移相比拟或者较小时,光生电场和光电效率会显著增强.当l≈l0时,所有光生载流子均不是热载流子,都对光电流有贡献,此时光电流达到最大值.l0的值由反对称参数ζ和光激发的能量决定.基于固体能带理论的估算表明l0的范围在10—100 nm之间[38],这暗示着铁电光伏器件在纳米尺度的应用前景.

3.2 体光伏效应

未掺杂单晶样品中的光伏效应被称为体光伏效应. 最早关于体光伏效应的报道出现于1956年[41],对BaTiO3单晶样品的光电流测量结果表明,光电流的值与样品的宏观电极化强度和方向密切相关.类似的实验结果在其他具有非对称中心的材料中也被发现,例如LiNbO3,LiTaO3以及被广泛关注的BiFeO3.

最早试图解释体光伏效应的理论模型认为铁电体中可能存在反对称的散射中心[42].如图3(a)所示,铁电体中随机分布着一些取向一致的楔形散射中心.即使仅存在载流子的随机扩散和漂移,铁电体内也会出现净电流.但是,由于熵增原理的限制,基于这一机制产生的电流在实空间上是局域的,并且不能持久.

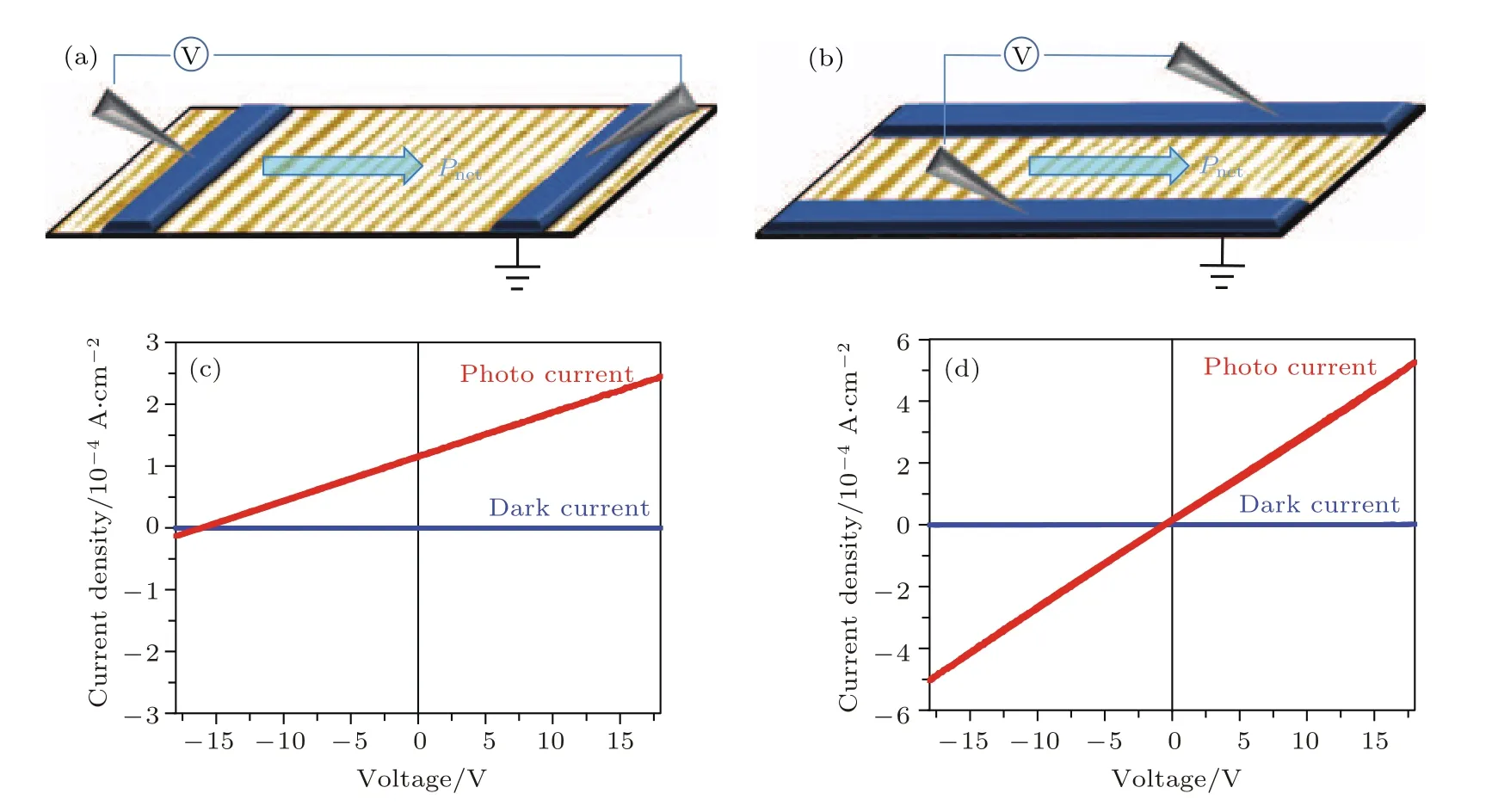
另一个理论模型则基于静电势的不对称[43],图3(b)显示电子和空穴的扩散过程,此时吸收中心的势具有明显的各向异性(可由电极化导致).当载流子吸收光子从E0态被激发至E态,若E

图3 体光伏效应模型[10],当(a)楔形散射中心[42]、(b)不对称的势阱[43]和(c)自旋轨道耦合作用[44]存在时净电流的产生Fig.3.Models for the bulk photovoltaic e ff ect[10]:(a)Asymmetric carrier scattering centres,resulting in a net fl ow from randomly drifting carriers,following Belinicher[42];(b)asymmetric potential well at a carrier generation centre;photogenerated carriers have a preferred direction of exit,following Lines[43];(c)relativistic splitting of the conduction band minimum establishes two distinct channels for electron excitation,polarized light promotes electrons preferentially to one channel,following Fridkin[44].

研究者认为当铁电体中存在较强的自旋-轨道耦合时,体光伏效应有着不同的物理起源[44].在这一机制中,同样需要晶体反演对称性的破缺[45].当自旋-轨道相互作用较弱时,所有的价带电子在吸收足够的光子后被激发的概率相等.但如果自旋-轨道耦合作用较强,在Rashba自旋轨道耦合作用下,导带进一步劈裂(如图3(c)所示),光生载流子的动量依赖于自旋,即不同极化的光照射将导致净电流,例如顺时针极化的光将激发kz>0的电子,而逆时针极化的光将激发kz<0的电子.由于价带和导带由不同的轨道所贡献,因此电子和空穴的自旋劈裂并不相同.当材料中含有重元素(Pb或Bi)时,自旋轨道耦合作用将变得更为重要,近年来对CH3NH3PbI3的研究正说明了这一点[46,47].

图4 与(a)有反演中心的晶体对比,(b)无反演中心的晶体中载流子具有非对称的动量分布,并产生净电流[37]Fig.4.(a)Isotropic and(b)anisotropic nonequilibrium carriers momentum distribution in centrosymmetric and noncentrosymmetric crystals corresponding to the classical and bulk photovoltaic ef f ects,respectively[37].

以上的三个物理模型虽然描述不同,但本质上都认为净光电流的产生是由于晶格势中运动的光生载流子具有不对称的速率(动量)导致.近来,有观点指出,净光电流的产生还可能与不对称的电子密度相关.载流子在能量空间里的激发,也伴随着实空间里的“虚”位移,即位移电流模型.事实上,位移电流导致的体光伏效应已经在铁电体[48−51]、量子阱[52]、有机晶体[53]和两维界面[54]等多种体系中发现.von Baltz和Kraut[55]首先提出用位移电流模型解释BaTiO3中的体光伏效应,在理论上很快用格林函数方法[56],在非线性光学的理论框架[57]下推导出位移电流的表达式.Young和Rappe[26]重新推导位移电流的表达式,使其可被用于第一性原理计算,并首次将计算得到的位移电流的值直接与实验结果相比较.在后来的第一性原理相关工作中,位移电流被认为是铁电体体光伏效应的主要贡献[24,58−62].

3.3 反常光伏效应

正如前文所描述,在传统的半导体器件中,能够获得的光电压一般被光吸收材料的能隙所限.但是,1946年Starkiewicz等[63]在PbS薄膜上的实验结果却首次打破了这一规则.紧接着,类似的实验结果也在CdTe,ZnTe和InP多晶样品中被报道[64−66].而对大量铁电薄膜光伏效应的研究表明,导致光伏性能提高的因素纷繁复杂,薄膜的铁电性能[67−70]、界面的结构和状态[70−74]、薄膜厚度、晶粒和电畴尺寸等尺度效应[67]以及空间电荷效应[69]等,都会对铁电薄膜的光伏性能有明显的影响.在已有的实验结果中,上百倍甚至上千倍于材料本征能隙的光电压被发现,光电流也得到提高,但光伏性能的改善敏感于样品的制备条件,因此实验结果很难被重复.目前还无法用统一的模型解释以上所有的实验现象,但研究者普遍认为这些显著的光伏效应,并不是材料本身所具有的,而更多地与材料的纳米或微米结构相关,区别于体光伏效应,称之为反常光伏效应.并大致可以归结为以下三种外禀因素.

1)铁电畴的畴壁.在铁电体中,光生载流子的分离由材料自身的电极化强度所驱动,畴与畴间产生电场.如图5所示,Yang等[25]在研究BiFeO3薄膜光伏效应时发现,BiFeO3中的光生电压随着极化方向上畴壁数量的增加线性增加.而垂直于极化方向上则没有观察到明显的光伏效应.简单估算可以发现,垂直于畴壁方向的电极化强度分量在畴壁处产生约10 mV的电压,畴壁宽度约为2 nm,因此电极化在畴壁处产生的电场高达5×106V/m,远大于传统半导体p-n结中的内建电场,可以驱动光生载流子的分离,产生反常光伏效应.由于铁电体中电畴数目很多,在电场的作用下,被电极化的畴首尾相连,畴壁如同一个个串联起来的纳米尺度的微电池.若这些铁电畴壁用串联的方式叠加起来,光生电压也可以沿着电极化方向逐渐累加,输出电压是每一个单元的和.当电极间距离越大,铁电畴壁越多,光照下产生的光生电压也就越高,这一模型可以很好地解释反常光伏效应.

图5 与畴壁相关的反常铁电光伏效应[25] (a)电极方向垂直于畴壁,(b)平行于畴壁;(c),(d)分别是图(a)和(b)中相应的I-V曲线Fig.5.Schematics of the anomalous photovoltaic ef f ect with(a)electrodes perpendicular to the domain wall and(b)electrodes parallel to the domain wall.The corresponding photocurrent-voltage curve for the devices in(a)and(b)are shown in(c)and(d),respectively[25].

2)肖特基结.当铁电体和金属电极相互接触时,界面处的能带将会发生弯曲,即肖特基势垒.起源于能带弯曲的内建电场可能驱动光生电子-空穴对的分离,产生光电流.显然,光电流强度主要由肖特基势垒的高度和电极附近耗尽层的宽度决定[72,75].与传统半导体太阳能电池类似,这一机制所产生的光生电压仍然受到铁电体本征能隙的限制.当采用不同电极构建铁电薄膜光伏器件时,由于上下两个电极与铁电体构成的肖特基结并不相同,产生的光生电压和电流不能相互抵消,这一效应将变得格外重要.例如,已有实验报道,在具有垂直结构的铁电光伏器件中光伏效应的增强可以归结为这一机制的贡献[76].另一方面,金属电极和铁电体界面处的肖特基势垒高度与铁电体的电极化强度相关,因此可以利用外加电场对肖特基势垒的高度进行调控,从而影响光生电压[73].由Au/BFO/Au构成的具有垂直结构的铁电二极管中,光生电流及光生电压都随着电极化方向的变化而变化[77].

3)退极化场效应.当铁电薄膜被极化时,薄膜表面具有高密度的极化电荷.当铁电薄膜与金属或半导体接触时,剩余极化所引起的表面电荷被金属或半导体中的自由电荷部分屏蔽,铁电薄膜内仍留下退极化场.退极化场可能具有很大的值.在BaTiO3薄膜(10—20 nm)中,当采用SrTiO3作为电极,BaTiO3中的退极化场高达45×106V/m[78].显然,这么强的退极化场可以驱动光生载流子的分离.退极化场的大小主要与铁电体的自发电极化强度、介电常数、厚度和电极的介电常数相关[74].越强的退极化场将产生较高的光生电压.

为了避免结型器件中界面态的控制问题,还有的研究者另辟蹊径,直接采用铁电体-半导体耦合方式构建器件[79].如图6所示,分离光生载流子的内建电场由电极化的纳米尺度电偶极子所形成的极化电场提供,利用包裹电偶极子颗粒的半导体吸光材料产生光生载流子.显然,在这一结构中,光生载流子的产生和分离被区分在不同材料内进行.电偶极子的作用仅是提供分离光生载流子的电场,并不参与光吸收,也不必考虑载流子在其中的输运问题.因此,纳米尺度电偶极子和半导体间不需要很好的电接触,可以降低对界面态的控制要求,在不削弱内建电场的同时,显著降低工艺难度和成本.理论计算表明[79],合理浓度的CdS纳米颗粒可以产生均匀且足够强的宏观电场,电场达到3×104V/cm,与理想p-n结内建电场相当.目前,实验上已在这一体系中获得超过8%的转换效率[80].

图6 偶极子极化产生的电场示意图[79]Fig.6.The electric f i eld induced by the electric dipole[79].

综上所述,铁电薄膜中的光伏效应可按照其起源分为体光伏效应和反常光伏效应,并存在多种物理机制.实验上测量得到的铁电体光伏效应可能来自于多种机制的贡献.因此,实验工作者的困惑在于如何区分体光伏效应和各种反常光伏效应的贡献.值得庆幸的是,现代极化理论的发展使研究者可以利用第一性原理方法计算各种不同机制对光伏效应的贡献,计算得到的结果已能与实验初步符合[26].

4 钙钛矿结构氧化物

大部分铁电体都具有钙钛矿结构,一般由三种元素组成,分子式可以表示为ABO3.B位阳离子和氧离子形成BO6八面体结构,通过分享顶点原子的方式形成三维空间结构.高温时,钙钛矿结构的铁电体大多具有高对称性的晶体结构,不表现出铁电极化.当温度降低,晶体结构发生畸变,转变为对称性较低的相,例如,长方、正交、菱面结构,并具有铁电性或反铁电性.由于钙钛矿结构氧化物铁电体同时具有长程序和短程序,它们的相图一般都非常复杂[81].大部分钙钛矿氧化物都是具有宽带隙的绝缘体,高温时以离子导电为主[82,83].对于离子型导电的氧化物,可以利用变价掺杂增加空位浓度而不是电子或空穴浓度.目前已有的实验结果表明基于钙钛矿氧化物的太阳能电池能量转换效率较低.例如基于体光伏效应的单晶BaTiO3太阳能电池,仅有10−7的极低能量转换效率[37].然而,近年来,通过减少层厚,优化畴壁结构和电极界面结构等方式,引入各种反常光伏效应,钙钛矿结构氧化物铁电体的光电能量转换效率得到显著提高[84].

阻碍钙钛矿氧化物铁电体实际应用的最主要因素之一是宽能隙,至少3 eV的能隙宽度导致其主要吸收波段在紫外区域.由于紫外光对太阳光谱的贡献仅为8%,因此目前在宽带隙铁电体中获得的最高能量转换效率仅为1.25%,这一数值是在PbZrTiO3与窄带隙的非晶硅薄膜的复合结构中得到的[85].针对这一缺陷,已有研究者对钙钛矿结构氧化物进行能带工程调控,使这些氧化物既保持良好的铁电性质,又有合适的能隙进行光吸收,从而提高光电转换效率[86,87].例如,相对于传统铁电材料,BiFeO3的能隙减小为2.7 eV,但仍保持有较大的铁电极化,同时具有奇异的线性和非线性光学响应[88]以及光伏效应[28,29,51,76,77,89−91].当用Cr替换BiFeO3中的部分Fe时,所形成的双钙钛矿结构Bi2FeCrO6光学带隙变化幅度可达几个eV,将能量转换效率提高至8.1%[84].

5 钙钛矿结构卤化物

杂化钙钛矿卤化物以极高的光电能量转换效率吸引着研究者以极大的热情投入到一个新的领域.自杂化钙钛矿卤化物首次作为光伏材料被报道以来[30],非晶和薄膜结构的器件研究已经获得显著进展[31−33,92−95],近来报道光电转换效率甚至已经超过20%.杂化钙钛矿卤化物的结构与钙钛矿氧化物类似,卤素原子取代氧离子,导致阳离子价态的平均值为+3.以CH3NH3PbI3为例,能带结构计算表明,能量最高的价带由I 5p带贡献,这导致价带顶能量高于钙钛矿氧化物.Pb离子的自旋-轨道耦合作用较强[96],导带的进一步劈裂使导带底的能量也明显低于钙钛矿氧化物.以上两种因素共同作用导致钙钛矿卤化物的光学能隙远小于具有同样结构的氧化物[47,97],可见光区域吸收强度显著增强[98].同时,钙钛矿结构所特有的丰富的物理和化学性质仍得到保留.

这类材料的另一个特别之处在于占据A位的不再是无机离子,而是有机分子,毫无疑问,这将引入额外的自由度.即使BX6八面体形成的三维结构仍可以导致铁电极化的出现,但晶体的对称性被明显降低.已有研究表明,CH3NH3分子具有较大的电偶极矩,对晶体的电极化强度以及优良的光伏性能有重要的贡献[99].A位有机分子的取向也会导致材料结构的变化[100].不仅如此,通过改变有机分子的大小,卤化物的结构发生改变,能隙也会随之得到调节[98].例如,尺寸较大的阳离子导致三维结构无法保持,断裂为二维层状结构[101−103].仅当选取尺寸较小的离子作为阳离子时,三维结构才是稳定的.

对钙钛矿结构卤化物器件的光伏性能研究发现,J-V曲线表现出特殊的电滞行为[104],离子扩散和铁电性被认为是导致这一异常现象的原因.目前不仅在实验上已经观测到铁电畴的存在[105],第一性原理计算结果也表明这类材料具有较大的自发电极化强度,量值可与无机钙钛矿材料相比拟[99].A位有机分子电偶极矩的取向无序随着温度和应力的改变而变化,这无疑增加了这类材料的复杂程度.研究者还利用第一性原理方法对CH3NH3PbI3的位移电流进行计算,发现在可见光区域的显著体光伏效应是一般钙钛矿氧化物的三倍,并且这一效应明显依赖于A位有机分子电偶极矩的取向[106].

6 自旋相关的铁电光伏效应

研究者不仅致力寻找具有高铁电极化强度、窄带隙和高输出功率的极性半导体材料,还试图引入新的自旋自由度,利用电场和磁场同时对光伏器件进行调控,丰富光伏器件的多功能性,发展新型光敏感多功能器件.双钙钛矿结构氧化物为这一方向的研究提供了广阔的研究平台.

除了目前已受到广泛关注的Bi2FeCrO6以及六角对称性的锰氧化物[107]外,近年来,大量LiNiO3型铁电和多铁材料被成功合成,例如Zn-SnO3[108],ZnTiO3[109],PbNiO3[110],ScFeO3[111]和Zn2FeTaO6[112].LiNiO3型结构是一种高畸变钙钛矿结构,具有菱面体对称性,空间群类型为R3c,当选取不同阳离子A位和B位时,相邻氧八面体的反向旋转和阴阳离子的相对位移将改变较大,并具有不同的铁电性和磁性质[113−119].ScFeO3即是其中一种性质较为特别的材料,它不仅具有较高的铁电极化强度,还具有弱铁磁性,这在已经发现的多铁性材料中并不多见.我们选取ScFeO3为母体材料,用另一种磁性离子对B位离子进行掺杂和替换,试图在保持母体所具有的高铁电极化强度的同时,对能隙进行调控,并引入自旋自由度[22].第一性原理计算结果表明,(0.17 6 x 6 0.83)具有较高的铁电自发极化强度(100µC/cm2)、弱铁磁性(磁化强度约为170 emu/cm3)以及适中的带隙宽度(1.8 eV).由于明显改善的可见光波段吸收,我们预测这一材料将优于传统的钙钛矿氧化物铁电体和多铁性材料,甚至是目前广受青睐的有机-无机杂化钙钛矿卤化物[120](图7).

图7 已研究的铁电光伏材料的铁电极化强度和能隙宽度[22]Fig.7.Map of ferroelectric polarization and band gap of popular polar materials[22].

更为重要的是,考虑如图8(a)所示的具有不同自旋的光生载流子,ScFe1−xCrxO3的能带计算结果表明,吸光后产生的光生载流子具有百分之百的自旋极化率(图8(b)).显然,如果利用ScFe1−xCrxO3制备光伏器件,光电流也将是百分之百被自旋极化的,因此ScFe1−xCrxO3可能被应用于光自旋电子学的器件中,实现显著的多功能性.如图9(a)所示,我们基于ScFe1−xCrxO3进一步设计具有典型三明治结构的太阳能电池,模型计算发现不同的电极化方向会导致太阳能电池内静电势的分布发生变化(图9(b)),从而导致具有显著差异的整流行为(图9(c)).图9(d)表明仅考虑反常光伏效应,在这一体系中计算得到其能量转换效率高达9.0%.可以预期,如果再叠加上体光伏效应的贡献,基于ScFe1−xCrxO3的光伏器件将具有显著的优势.另一方面,计算表明基于这一太阳能电池的输运行为表现出明显的自旋极化的特征,几乎在整个可见光光谱范围内产生的光电流都是100%自旋极化的,这为该类型的光伏器件在光伏产业和自旋电子学领域的应用开辟了新的途径,例如高效太阳能电池、自旋光伏器件等.

图8 (a)自旋极化的ScFe1−xCrxO3中光生载流子的弛豫过程;(b)光转换效率的自旋极化率[22]Fig.8.(a)Relaxation processes of photoexcited electrons in spin-polarized ScFe1−xCrxO3;(b)spin polarization of the photo conversion efficiency[22].

事实上,不仅铁电体的光伏效应可能受到自旋自由度的调控,它的其他非线性光学性质也被发现与自旋自由度相关.我们对具有四方对称性的BiFeO3薄膜[121,122]和块材[88],Bi2FeCrO6[114],BiCoO3[123]和PbVO3[124],甚至极性材料BiInO3,BiAlO3[125]和Bi2ZnTaO3[126]的非线性光学性质进行了计算.如图10所示,以BiFeO3块材的计算为例,我们发现介电常数的实部和虚部能与实验符合得很好,说明第一性原理计算结果的可靠性[88].进一步,第一性原理计算结果表明,这些材料的二次谐波产生(second harmonic generation,SHG)系数受到体系磁有序的影响,当磁有序从非铁磁序转变至铁磁序时,SHG系数明显增强,这表明可以利用磁场对它们的非线性光学性质进行调控,预示着多铁性材料光、磁和电的多功能性.归根结底,自旋自由度对多铁性材料非线性光学性质的调控起源于磁电序参量间的耦合作用.以BiFeO3为例,其铁电性主要来源于A位Bi离子的孤对电子,而铁磁性则主要由B位Fe离子的贡献.显然,铁电性和铁磁性具有截然不同的物理起源,毫无疑问,这意味着在BiFeO3中磁电耦合效应较弱.但即使在基态时电极化和磁化强度之间的耦合非常小,在光频段磁电耦合作用却变得十分重要,导致多铁性材料可能具有非常有趣的磁电线性和非线性光学性质.

图9 (a)ScFe1−xCrxO3三明治结构作为光伏器件的示意图;(b)铁电极化反转导致静电势的改变;(c)J-V曲线;(d)PCE随厚度的变化[22]Fig.9.(a)Illustration of generation and separation of photo-induced spinpolarized carriers in a ScFe1−xCrxO3-based sandwich structure.(b)Potential prof i le for ScFe1−xCrxO33(here,x=1/2),with the ferroelectric polarization pointing to the right-hand-side electrode.The dotted line shows the situation without ferroelectric polarization.(c)Current-voltage relationship of this sandwich structure with 100-nm-thick ScFe1/2Cr1/2O3.The shaded area is the maximum power output.(d)PCE as a function of the thickness of ScFe1−xCrxO3(1/6 6 x 6 5/6).Here,SFCO is for ScFe1−xCrxO3,SRO is for SrRuO3,RP and LP are for the ferroelectric polarization pointing to the right and the left,respectively[22].

图10 计算得到的BiFeO3块材实部和虚部,计算结果(红色实线)与实验数据(蓝色圆点)符合较好[88]Fig.10.Real and imaginary parts of the averaged dielectric function.Ab initio results with U=7 eV(red solid line)in good agreement with experimental data(blue round dot)[88].

7 结 论

铁电光伏效应因为其重要的应用前景和丰富的物理内涵受到国内外研究者的广泛关注.目前,研究者已经对铁电光伏效应的多种机制有比较深入的认识,找到了提高光伏效应的途径,探索具有高光电转换效率的新材料,并积极地通过引入新的自由度,实现铁电光伏器件的多功能性.但是,要将铁电光伏效应应用于实际的太阳能器件,还有很多的问题亟需解决.例如,如何区分多种机制对铁电光伏效应的贡献仍然比较困难,这无疑为准确、有效地提高光电转换效率带来不小的难度.如何利用能带工程原理结合薄膜制备技术,搜寻能隙较小、厚度较薄但铁电性优良的铁电体,实现较高的光电能量转换效率;如何更加深入地理解新的自由度(自旋自由度)在光生载流子的产生、输运和复合等过程中所扮演的角色及其对光伏效应的影响,这将帮助我们实现和开拓铁电光伏器件光敏感的多功能性.这些都是值得进一步研究的问题.