区域大气加权平均温度模型构建与适用性分析
2018-09-06王朋远李飞郑南山
王朋远,李飞,郑南山
(1.珠海市测绘院,广东 珠海 519015; 2.广东省科学技术职业学院 建筑工程学院,广东 珠海 519090; 3.中国矿业大学 环境与测绘学院,江苏 徐州 221116)
0 引 言
作为地球大气的重要组成成分,水汽的三相变化对于地球上生命的重要意义不言而喻。各种天气系统的演变、灾害性天气的监测和预报、区域乃至全球气候变化等均与大气中水汽含量有着十分密切的关系。传统的大气水汽探测手段受探测精度和时空分辨率的限制,不能满足水汽复杂时空变化的监测要求[1]。随着全球导航卫星系统(GNSS)技术的不断发展,其在很多领域得到了广泛应用,而利用地基GNSS反演大气水汽发展成为一门新兴技术。与传统水汽探测方法相比,GNSS水汽反演技术具有精度高、成本低、全天候作业、时空分辨率高和实时性强等诸多优势,能够有效弥补传统探测手段的不足,为空间大气水汽探测提供更及时、全面、可靠的信息资料。
利用地基GNSS技术反演水汽,首先要从对流层天顶总延迟中分离出天顶静力延迟,得到与水汽含量直接相关的天顶湿延迟量,通过转换参数将天顶湿延迟量转化为气象学中的重要气象参数——大气可降水量。转换参数的准确度直接影响大气可降水量的反演精度,而转换参数与大气加权平均温度直接相关。加权平均温度由气象探空站采集的气象数据确定,由于探空观测的时空分辨率较低,一般采用长期的气象数据资料建立加权平均温度经验模型。由于对流层存在区域性差异,不同区域不同时期的气象参数差异较大。研究表明[2-9],根据不同区域的气象参数建立适合本地区的加权平均温度模型有利于提高转换参数的准确度,进而提高GNSS水汽反演精度。本文旨在对区域加权平均温度模型的建立、模型的精度和适用性进行研究。
1 加权平均温度获取
文献[10]提出利用探空资料观测的温、湿、压资料计算加权平均温度的方法,即由探空站上空水汽压和绝对温度沿天顶方向积分可得,其算式为
(1)
式中:e和h分别为测站天顶方向上水汽压,hPa和绝对温度(K);z为探空站上空的垂直高度(m)常规探空资料提供的大气压,位势高度,气温,露点温度,相对湿度等值均为分层测量得到,为不连续值,通常将上式离散化,采用数值积分的形式,即
(2)
式中:ei、Ti分别为第i层大气的平均水汽压和平均气温;Zi为第i层大气层的厚度,单位均同上。这里,水汽压值可以根据露点温度td采用下式计算[11]:
(3)
(4)
探空观测数据可以从网站(http://weather.uwyo.edu/upperair/seasia.html)上获取,由于香港Kings Park探空站(编号45004)的观测资料层次丰富,低层数据间隔小,顶层数据高度能达到二十千米,整体数据质量相对较高。因此,本文基于香港探空站2012-2015年总体探空数据对构建区域化加权平均温度模型进行研究。利用Linux系统的文本传输命令curl按月份批量下载,并借助cat、awk、grep等相关指令将数据进行合并和格式转化。利用MATLAB对数据进行提取预处理,通过编程实现建模、解算和分析。
2 区域加权平均温度建模
2.1 加权平均温度与地面气象因素的关系
由式(1)可知加权平均温度Tm是水汽压e和气温T的积分,可以推断,加权平均温度与地面气象因素之间存在某种相关关系,利用2012-2015年香港探空数据对加权平均温度Tm与地面各气象因素的关系进行简要分析。图1(a)、(b)、(c)表明,Tm与地面气温Ts、露点温度Td和水汽压e具有良好的正相关,由图1(d)可知Tm与地面大气压P呈较好的负相关。Tm与各气象因素的相关系数如表1所示。

因素Tm-TsTm-TdTm-eTm-P 相关系数0.8130.8030.722-0.690
2.2 区域加权平均温度模型建立
基于Tm与各气象因素的相关性分析,利用香港探空站2012-2015年共2896个样本的数据建立香港地区加权平均温度的单因素和多因素模型。
2.2.1 单因素模型
图2是Tm与Ts的时间演变关系图,可以看出,加权平均温度与地面气温的变化趋势和升降幅度保持同步,二者的峰值和谷值对应得很好,加权平均温度Tm普遍比地面气温Ts低。利用加权平均温度Tm与测站地面温度Ts之间的线性相关关系建立回归公式,仍是获取加权平均温度本地化模型的重要手段。究其原因有:1)地面温度Ts较其它地面气象因子较易获取,且与Tm线性关系明显;2)诸如GAMIT、BERNESE等高精度GPS数据处理软件采用的加权平均温度公式为Tm与Ts的关系式,方便使用。
基于以上分析,本文建立基于地面气温的本地化加权平均温度单因素模型,其形式为
Tm=a+b·Ts,
(5)
为探究最优回归方程系数,这里采用统计学中的最小二乘原理,系数a,b须满足:
(6)
令
(7)
(8)
解得
(9)
(10)
由图2可以看到,Tm与Ts呈现出以年为周期的变化规律,分别以单年份和多年份的观测数据为基础建立相应年份的回归模型,并将Bevis公式应用于该地区进行比较分析,结果如表2所示。
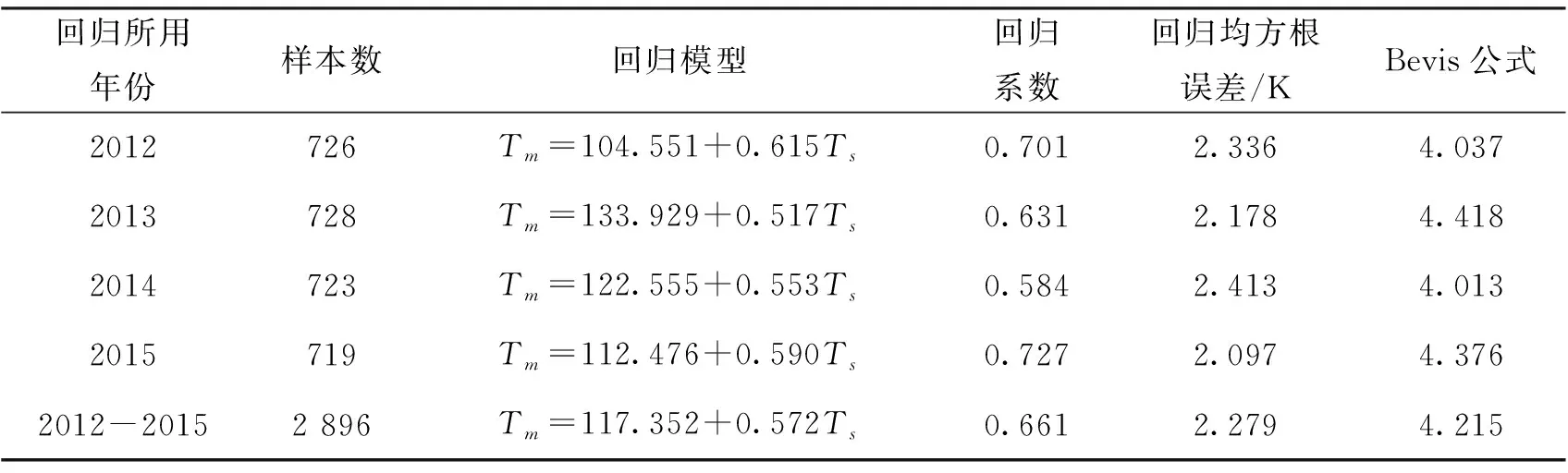
表2 单因素Tm回归模型统计结果
地基GNSS气象学研究中,要求可降水量的反演精度达到mm级,而3.4 K的加权平均温度Tm误差引起的可降水量误差约为1 mm[2].Bevis公式应用于香港地区时Tm误差均超过4 K,不能满足精度要求。因此该公式不适用于香港地区水汽反演。基于香港地区气象数据建立的区域Tm模型回归均方差小于2.5 K,模型精度比Bevis公式高,对比不同年份的统计结果发现,本文建立的区域Tm模型误差比Bevis减小了一半左右。以2012-2015年数据回归建立的单因素模型的拟合残差分布如图3所示,可以发现残差分布多集中在-2~2 K之间,少部分残差偏大可能是由于观测资料粗差引起的,总的来说本文建立的单因素模型精度较高。
2.2.2 多因素模型
相应于单因素模型,基于相同的观测数据采用多元回归分析方法建立香港地区多因素模型,结果如表3所示。对比表2和表3所示,对应年份的多因素模型的回归均方根误差均比单因素模型小,多因素模型精度略优于单因素模型,但多因素模型要求获取的气象参数较多。
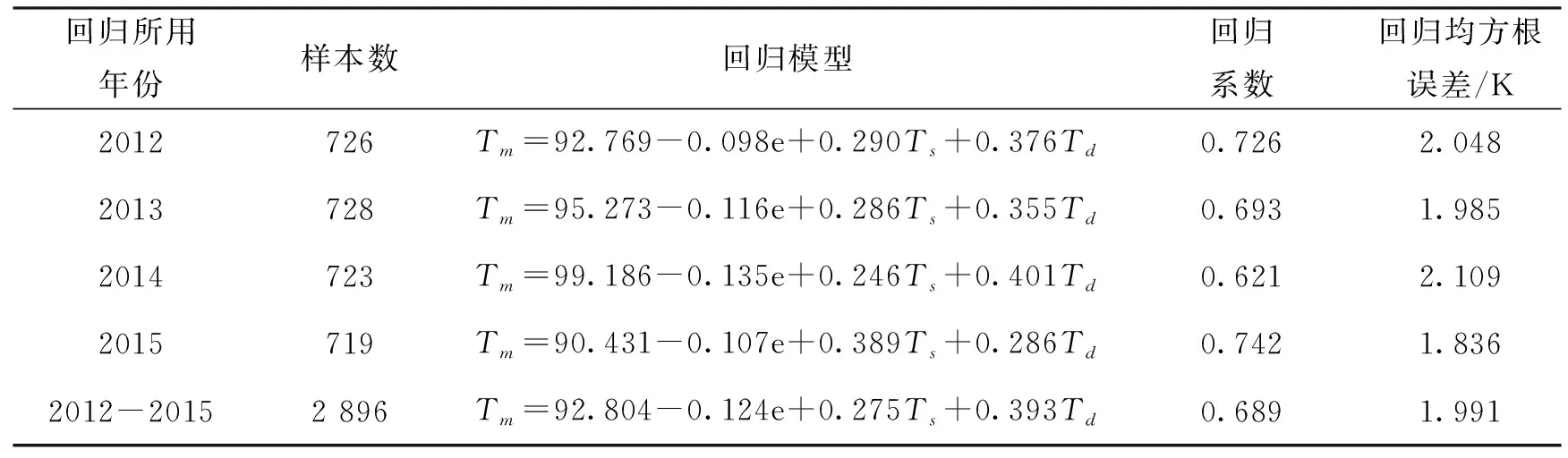
回归所用年份样本数回归模型回归系数回归均方根误差/K 2012726Tm=92.769-0.098e+0.290Ts+0.376Td0.7262.048 2013728Tm=95.273-0.116e+0.286Ts+0.355Td0.6931.985 2014723Tm=99.186-0.135e+0.246Ts+0.401Td0.6212.109 2015719Tm=90.431-0.107e+0.389Ts+0.286Td0.7421.836 2012-20152 896Tm=92.804-0.124e+0.275Ts+0.393Td0.6891.991
为了验证回归模型的预测精度和适用范围,用2012年数据建立的回归模型来逐年预测2013-2015年Tm,预测结果如表4所示。可以看到,无论是单因素回归模型还是多因素回归模型,预测均方差与相应年份的回归均方差相差均小于0.4 K,预测精度很高,与基于相应年份建立的区域Tm模型差异不大。因此,区域Tm模型一次建立可长期使用。相比之下,多因素回归模型的预测精度略高于单因素模型的预测精度,在气象参数获取充分的情况下,可采用多因素Tm回归模型。
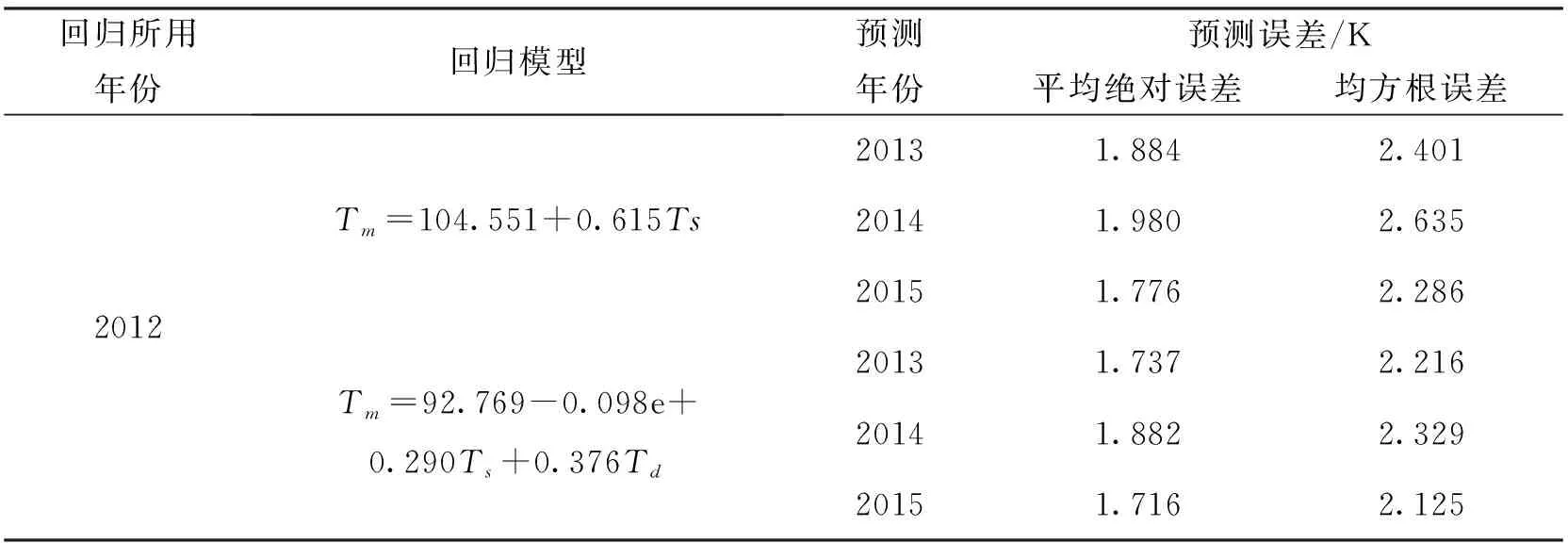
表4 回归模型的预测误差统计结果
3 区域加权平均温度模型的适用性分析
由上节讨论可知,Tm多因素模型比单因素模型精度略高。考虑到多因素模型要求获取的气象参数较多,而地面气温比其它气象因素更容易获取,实际应用时多采用单因素Tm模型。单因素模型简单,精度满足要求,普遍应用于目前的高精度GNSS数据处理软件。
为了验证本文建立的Tm单因素模型的适用性,与香港地区目前可用的Tm模型进行对比分析。文献[2]根据香港地区1996-1997年观测资料首次建立了香港地区Tm回归模型,这里记作Tm_l模型;文献[8]利用2003-2009年香港探空站资料建立了Tm回归模型,记作Tm_w模型;将本文建立的单因素回归模型记作Tm_b模型。三个模型的比较结果如表5所示。
由表5可以看出,Tm_b模型精度最高,Tm_w的模型精度和Tm_b相当,Tm_l模型精度较差,其原因可能是建立该模型采用的统计样本年份过早,现在的气候条件较当时的气候条件已发生了变化,而且Tm_l模型采用的样本量较少。相比之下,Tm_w模型采用03至09年七年的统计数据,样本更充分,且与现在的气候条件更接近,其精度与Tm_b模型差异不大,该模型依然有较好的适用性。

表5 香港地区不同Tm模型的比较
4 结束语
通过对香港探空站2012-2015年数据资料的分析处理,建立了香港区域加权平均温度单因素和多因素模型,并对模型精度和适用性进行了对比分析。结果表明,多因素模型精度优于单因素模型,但显著程度不高,而多因素模型需要的观测量较多,实际应用中可采用单因素模型;Bevis经验公式应用于香港地区时不满足精度要求,而加权平均温度模型一旦建立,可供较长时间内使用。与香港地区目前可用模型的对比表明,本文建立的模型精度更高,在地基GNSS水汽反演中为获取高精度大气可降水量,可利用较近年份探空数据建立回归模型。
