改进人工蜂群优化的K均值图像分割算法

李海洋 何红洲

文章编号： 2095-2163（2018）03-0045-05中图分类号： 文献标志码： A

摘要： 关键词： （School of Information Engineering， Mianyang Normal University， Mianyang Sichuan 621000， China）

Abstract： In the image segmentation， K-means clustering algorithm has the disadvantage of low accuracy and poor stability. The hybrid algorithm based on artificial bee colony and K-mean tend to be too inefficient to meet the application requirements. To cure the above problems， a new image segmentation algorithm called IABC-K is proposed in this study. The artificial bee colony algorithm is improved according to its different characteristics in honey source renewal and mining. An adaptive neighborhood search mechanism associated with optimal fitness is adopted to improve the speed of honey source renewal. A linear decreasing neighborhood search strategy associated with optimal fitness is adopted to improve the quality of honey source mining. Experimental results show that IABC-K algorithm is superior to other similar algorithms in terms of quality， efficiency and stability. IABC-K algorithm has better image segmentation quality and higher image segmentation efficiency. It can be applied in image processing field with high quality and performance requirements.

Key words：

基金項目：

作者简介：

收稿日期： 引言

K均值聚类算法是聚类问题研究的经典算法，常应用于图像分割[1]。但K均值聚类算法的聚类结果往往依赖于初始值的选取，图像分割质量较低[2]。针对K均值聚类算法的缺点，很多研究人员采用进化技术对K均值聚类算法进行优化。进化技术中，主要包括有：遗传算法[3]、粒子群优化[4-5]、人工蜂群优化[6]（artificial bee colony， ABC）等。其中，ABC算法性能优异，全局寻优能力强，能比遗传算法、粒子群优化算法更快收敛于最优解[7]。

在ABC算法优化K均值聚类的研究中，梁冰等[8]将与当前维度最优解差值的变化率作为权值，对蜜源的搜索公式进行了改进，提高了算法的鲁棒性和聚类精度。宋锦等[9]修改了ABC算法对蜜源的更新方法，获得了较好的图像分割质量。Shokouhifar等[10]利用ABC算法来调整模糊规则，使算法具有自适应特性。Cong等[11]通过变异操作增强了ABC算法的搜索能力，提高了算法的聚类质量。Bose等[12] 使用一种模糊隶属函数来搜索ABC算法最优解，用以初始化K均值聚类中心，使算法在收敛性、时间复杂度、鲁棒性和图像分割精度方面表现较好。赵文昌等[13]利用距离最大最小乘积方法对ABC种群进行初始化，并采用自适应搜索参数调整邻域搜索范围，得到了较好的图像分割效果。但是，上述混合聚类算法大都针对特定条件，并存在稳定性欠佳的问题，不能达到聚类质量和聚类效率同时提高的目的，因而难以应用在分割质量和分割效率要求较高的图像处理领域。

基于此，本研究提出一种新的ABC和K均值聚类的图像分割算法IABC-K。IABC-K算法分别改进了ABC算法的蜜源更新和蜜源开采公式，使其邻域搜索策略更符合不同进化阶段的要求，从而使算法获得了稳定性强、分割质量好、分割效率高的出色性能表现。

1相关算法

1.1K均值聚类算法

K均值聚类算法是从聚类样本X=xi∈Rd，i=1，2，…，n中随机选取k个聚类中心a1，a2，…，ak，将xi按最小距离分配到k个簇，其目标函数如式（1）所示：J=∑kj=1∑x∈Cjx-aj2（1）其中，x是每个簇内的样本。

当目标函数最小时，可根据式（2）更新k个聚类中心。数学公式具体如下：Cj=1N∑x∈Cjx（2）其中，N是第j个簇包含的样本数。

通过不断迭代，当k个簇的中心都不再变化或满足迭代条件时，可得到聚类结果。

1.2ABC算法

ABC算法通过模拟蜂群分工合作寻找最优蜜源的过程来求解优化问题，是一种基于蜜蜂群体智能的优化算法[14]。ABC算法求解优化问题的步骤如下：

步骤1种群的初始化。样本集X={xi∈Rd，i=1，2，…，n}表示待求解的优化问题，xi为d维向量；设算法最大迭代次数为MCN；每个蜜源的最大开采次数为limit。

步骤2随机选择蜜源，用来表示初始可行解，公式表述可见如下：Xji=Xjmin+rand0，1（Xjmax-Xjmin）（3）其中，j∈1，2，…，d；xji表示第i个可行解的第j维分量；rand0，1是区间0，1内均匀分布的随机数。

步骤3引领蜂在其对应的蜜源当前位置附近邻域内对蜜源进行更新，研究推得数学公式如下：Vji=Xji+φjiVji-Vjk （4）其中，k∈1，2，…，n，且k≠i；φji为区间-1，1内均匀分布的随机数，用来控制邻域搜索范围。

步骤4如果蜜源Vji=v1i，v2i，…，vdi的适应度优于蜜源Xji，则采用贪婪选择法用Vji代替Xji；如果蜜源Xji经过limit次开采后都没有更新，说明该蜜源质量较差，则蜜源Xji应被放弃，其对应的引领蜂转化为侦察蜂，并根据式（3）随机选择新蜜源。

步骤5在每个引领蜂更新蜜源后，跟随蜂在引领蜂种群内选择一只引领蜂，跟随其前往蜜源采蜜。跟随蜂选择引领蜂的概率计算如式（5）所示：pi=fi/∑ni=1fi（5）其中，fi为第i个蜜源适应度值。

然后，跟随蜂在被选蜜源位置附近采用式（4）开采蜜源。

步骤6若算法当前迭代次数t

2ABC算法改进

在ABC算法中，引领蜂和跟随蜂共用式（4） 实现蜜源的更新和开采，而式（4）中的邻域搜索范围控制系数φji是一个在区间[-1，1]内均匀分布的随机数，会对ABC算法性能产生影响，使算法收敛速度过慢或求解精度不高[15]。当ABC算法与K均值聚类算法相混合后，ABC算法的这种影响会被放大并传导至混合算法，造成混合算法整体性能下降。本研究根据ABC算法不同阶段特点，对ABC算法的蜜源更新及开采策略进行了改进，并设计给出了改进ABC算法与K均值混合算法步骤。

2.1蜜源更新策略

在ABC算法中，蜜源更新目的是通过适应度函数值判断可行解的优劣， 保持每个可行解优良性质。这一阶段，算法应尽量避免陷入局部最优，实现蜜源快速更新，才能获得算法高效性。但式（4）中φji是随机产生的。如果引领蜂所对应蜜源为优质蜜源而随机产生的φji较小，就会使该引领蜂寻优能力下降，并不断放弃优质蜜源；如果引领蜂所对应蜜源为劣质蜜源而随机产生的φji较大，就会扩大该引领蜂的邻域搜索范围，使算法迟迟不能收敛。本研究对原算法的蜜源搜索公式做出了改进，采用与最优适应度关联策略，在蜜源更新过程中加入搜索邻域优良个体信息，能使算法快速收敛于最优解。研究得到这一过程公式可表示为：Vji=Xji+φjifibest（Vji-Vjk）（6）其中，fibest是第i个蜜源的第j维分量的最优适应度值。

同时，为避免算法陷入局部最优，本研究采用了自适应策略，对φji的取值也提供了一定了改进，研究中将使用如下数学公式：

φji=φmin+φmax-φminfi-fminfavg-fminfi≤fmin

φmaxfi>fmin （7）

其中，φmin和φmax為常数，用以控制邻域搜索的最小、最大范围；favg和fmin为当前所有蜜源的平均适应度和最小适应度。

采用以上最优适应度关联的自适应搜索策略后，当fi与fibest相差较大时，可通过式（7）自动增大φji，避免算法陷入局部最优，使算法快速逼近最优解；当fi与fibest相差较小时，可通过式（7）自动减小φji，提高算法局部寻优能力，实现精细搜索。

2.2线性递减的蜜源开采策略

在ABC算法中，蜜源开采的目的是在每个可行解中继续寻优，找到最优解。在蜜源开采初期，算法应采用较大的开采系数，从而保持较强的全局寻优能力，快速逼近最优解；在蜜源开采后期，算法应采用较小的开采系数，实现细致的局部寻优。但式（4）中开采系数φji是随机变化的，与对蜜源开采阶段的要求不相适应。如果在蜜源开采初期，随机产生的φji比较小，就会降低算法的全局寻优能力，使算法迟迟不能逼近最优解；如果在蜜源开采后期，随机产生的φji比较大，则会造成对蜜源的过度开采，降低算法效率。针对这一问题，本研究对式（4）进行了改进。在数学理论上，即如式（8）所示：Vji=Xji+γ fibest（Vji-Xji）（8）其中，γ为邻域搜索范围调整系数，对应计算则如式（9）所示：γ=γmax-t×（γmax-γmin）tmax（9）其中，γmax和γmin为常数，用以控制邻域搜索最大最小范围，这里取γmax=0.9， γmin=0.3；t和tmax分别为当前迭代步数和最大迭代步数。

式（8）采用了最优适应度关联的搜索范围线性递减的策略，能使开采系数随进化步数逐渐降低。其优点是：在蜜源开采初期，γ相对较大，利于大范围搜索，能使算法快速逼近全局最优，提高算法效率；在蜜源开采后期，γ相对较小，利于算法实现局部精细搜索，提高算法寻优质量。

3IABC-K算法

经过对ABC算法的改进，结合K均值聚类，本研究提出了一种新的人工蜂群优化与K均值聚类混合算法IABC-K。

3.1算法思想

IABC-K算法首先将图像分割问题转化为ABC算法搜索最佳蜜源问题，然后采用改进蜜源更新和开采策略的ABC算法进行寻优，利用改进ABC算法全局寻优能力强的优点，使算法快速逼近全局最优。当算法逼近全局最优或得到指定阈值时，使用当前搜索到的全局最优解作为K均值初始聚类中心，将算法切换到K均值聚类算法，利用K均值聚类局部寻优精细的特点继续寻优，直至找到最优解。

3.2蜜源适应度计算

在进行图像分割时，首先将图像转化为d维数据点样本集，并根据式（3）随机选择n个蜜源作为优化问题解空间。其中，第i个蜜源的适应度计算方法如式（10）所示：fi=∑dj=1∑xi∈Cjxi-cj2（10）3.3算法切换

ABC算法切换至K均值聚类的时机由蜜源群体适应度方差σ2决定。在对蜜源的开采进程中，fi与favg将逐渐趋同，并使σ2逐渐变小。当跟随蜂搜索到最优蜜源附近时，σ2将小于某指定阈值。这时，可停止跟随蜂的开采工作，输出跟随蜂搜索到的当前最优解作为K均值聚类中心，进入K均值寻优阶段。σ2的计算如式（11）所示：σ2=∑ni=1fi-favg（11） 3.4算法步骤

IABC-K算法步骤如下：

步骤1初始化样本集X并设置引领蜂、跟随蜂和侦察蜂数量；设置MCN和limit初始值。

步骤2采用式（3）进行蜜源初始化，并根据式（10）计算初始化后的每个蜜源的适应度值fi，记录最优适应度值fibest。

步骤3根据式（7）计算φji，然后根据式（6）进行蜜源更新：若蜜源Vji优于蜜源Xji，则用Vji代替Xji；若Xji经limit次开采后无更新，则放弃Xji，其对应引领蜂转化为侦察蜂，根据式（3）随机勘探新蜜源并替代Xji，再按式（10）重新计算fi，记录fibest。

步骤4根据式（5）所得概率使跟随蜂选择引领蜂或蜜源。

步骤5根据当前进化步数t按式（9）计算γ。再根据式（8）进行蜜源开采。

步骤6根据式（11）计算σ2。若σ2不小于指定阈值，则转到步骤5，按式（8）继续开采蜜源；若σ2小于指定阈值，则算法转到K均值聚类，并以跟随蜂搜索到的k个当前最优解作为K均值聚类的初始中心，同时按式（1）计算每个数据点到各聚类中心距离，再按式（2）继续搜索更优解。

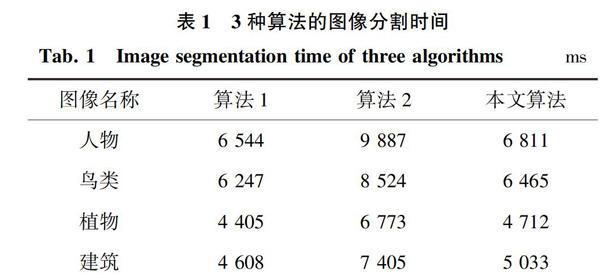
步骤7若算法当前迭代次数t

4实验结果和分析

本研究将IABC-K算法（以下简称本文算法）与其它算法进行了对比实验。参与对比的算法为K均值聚类算法（以下简称算法1），ABC与K均值聚类混合算法（以下简称算法2）。算法2和本文算法参数设置相同：种群大小为20；个体维度为5；limit取20；MCN取500。实验环境为Intel（R） Core（TM）i7 @2.67 GHz ＼＼RAM 4GB＼＼ Windows 7，仿真平台为Matlab R2012a。实验数据为伯克利图像分割测试数据集。研究中选取了4幅图像进行分割实验，结果如图1所示。

在图1中，图1（a）从左到右依次为实验图像原图，包括：人物（481×321；115 KB）；鸟类（481×321；104 KB）；植物（321×481；93.5 KB）；建筑（481×321；113 KB）。图1（b）～（d）分别为实验图像在算法1、算法2和本文算法下的分割结果。为了更好地比较3种算法的分割质量，给出了实验结果的局部放大图，如图2所示。

图2（a）～（d）分别为实验图像原图和算法1、算法2和本文算法分割实验结果的局部放大图。从图2（a）～（d）第一列可以看出，在箭头所指的人物左侧脸颊處，原图存在阴影，算法2和本文算法均较好地分割出了该阴影而算法1却丢失了该阴影；对人物鼻梁处的头发，算法1分割结果较为模糊，而算法2和本文算法较清晰。从图2（a）～（d）第二列可以看出，在箭头所指的鸟的翅膀处以及鸟的胸腹羽毛处，本文算法很好地保持了其轮廓的完整性，具有最好的分割效果；算法2也基本保持了轮廓的完整性但效果稍差，而算法1结果存在残缺。图2（a）～（d）第三列显示的是3种算法对植物图像的分割，可以看出，算法1和算法2结果中，树与海水背景相互混杂，树叶轮廓不完整；本文算法不但清楚地分开了树与海水背景，而且树叶轮廓较完整。图2（a）～（d）第四列显示的是3种算法对建筑图像的分割。在原图中，建筑楼层分为3层，但算法1已经分辨不出来；算法2虽然可以分辨但不够完整；本文算法的分割结果清晰完整，明显优于算法1和算法2。

本研究对4幅图像各重复了20次分割实验，并对比了3种算法的平均运行时间。实验运行结果可见表1。

图像名称算法1算法2本文算法人物6 5449 8876 811鸟类6 2478 5246 465植物4 4056 7734 712建筑4 6087 4055 033从表1可以看出，在对4幅图像进行分割时，算法1平均运行时间最少，算法2平均运行时间多于本文算法，说明本文算法的图像分割效率优于算法2、但低于算法1。

实验结果表明：本文算法图像分割质量优于算法1和算法2，效率略低于算法1而高于算法2。究其原因即在于：本文算法在ABC算法蜜源更新阶段引入了与最优适应度关联的自适应邻域搜索机制，增强了算法综合寻优能力，使算法能快速逼近最优解，提高了算法效率；本文算法在ABC算法蜜源开采阶段采用与最优适应度关联的线性递减策略，可有效匹配蜜源开采阶段的特点和要求，从而能提高算法寻优质量和效率；本文算法以ABC算法寻优结果初始化K均值聚类中心，解决了K均值聚类对初始中心的依赖问题，提高了算法稳定性。此外，本文算法效率略低于算法1，原因在于本文算法的复杂度要高于算法1。

5结束语

本文提出的IABC-K算法根据ABC算法在蜜源更新和蜜源开采阶段的不同特点，分别采取了与最优适应度关联的自适应蜜源更新策略和线性递减蜜源开采策略，取得了较好的图像分割质量和更高的图像分割效率。但如何改进ABC算法，有效解决图像分割存在问题，还有待深入研究。

参考文献

[1] MACQUEEN J. Some methods for classification and analysis of multivariate observations[C] // Proc. of 5th Berkeley Symposium on Math. Stat. and Prob. Berkeley：University of California Press， 1967：281-297.

[2] SIDDIQUI F U， ISA N A M. Enhanced moving K-means （EMKM） algorithm for image segmentation[J]. IEEE Transactions on Consumer Electronics， 2011， 57（2）： 833-841.

[3] 詹森， 秦大同， 曾育平. 基于遗传优化K均值聚类算法工况识别的混合动力汽车能量管理策略[J]. 中国公路学报， 2016， 29（4）： 130-137，152.

[4] 李海洋， 文永革， 何红洲， 等. 基于随机权重粒子群和 K-均值聚类的图像分割[J]. 图学学报， 2014， 35（5）： 755-761.

[5] LI Haiyang， HE Hongzhou， WEN Yongge . Dynamic particle swarm optimization and K-means clustering algorithm for image segmentation[J]. International Journal for Light and Electron Optics， 2015， 126（24）： 4817-4822.

[6] 柯钢. 基于增强蜂群优化与 K-means 的文本聚类算法[J]. 计算机应用研究， 2016， 33（8）： 2298-2302.

[7] KIRAN M S， HAKLI H， GUNDUZ M， et al. Artificial bee colony algorithm with variable search strategy for continuous optimization[J]. Information Sciences， 2015， 300：140-157.

[8] 梁冰， 徐华. 基于改进人工蜂群的核模糊聚類算法[J]. 计算机应用， 2017，37（9）：2600-2604.

[9] 宋锦， 高浩， 王保云. 改进人工蜂群算法在图像分割中的应用[J]. 电视技术， 2016， 40（8）： 8-14.

[10]SHOKOUHIFAR M，JALALI A. Optimized sugeno fuzzy clustering algorithm for wireless sensor networks[J]. Engineering Applications of Artificial Intelligence， 2017，60： 16-25.

[11]CONG T D， WU Zhijian， WANG Zelin， et al. A novel hybrid data clustering algorithm based on Artificial Bee Colony algorithm and K-Means[J]. Chinese Journal of Electronics， 2015， 24（4）：694-701.

[12]BOSE A， MALI K. Fuzzy-based artificial bee colony optimization for gray image segmentation[J]. Signal， Image and Video Processing， 2016，10（6）：1089-1096.

[13]赵文昌， 李忠木. 融合改进人工蜂群和K均值聚类的图像分割[J]. 液晶与显示， 2017，32（9）：726-735.

[14]秦全德， 程适， 李丽， 等. 人工蜂群算法研究综述[J]. 智能系统学报， 2014， 9（2）： 127-135.

[15]周新宇， 吴志健， 邓长寿， 等. 一种邻域搜索的人工蜂群算法[J]. 中南大学学报（自然科学版）， 2015， 46（2）： 534-546.

[16]YEH C C， YANG M S. Evaluation measures for cluster ensembles based on a fuzzy generalized rand index[J]. Applied Soft Computing， 2017， 57：225-234.（上接第44页）

[5] 陈昌领，冯晓东，邵惠鹤. 单生产线序贯多目的批处理过程短期调度的MILP建模[J]. 系统仿真学报，2001，13（S1）：69-71.

[6] 戴智杰，宋执环，宋春跃. 基于遗传算法的浸染生产排缸策略[J]. 运筹与管理，2006，15（2）：149-153.

[7] 莫丰勇，郝平，杨马英. 基于遗传算法的拉动式浸染生产动态排产策略[J]. 计算机应用，2008，28（S2）：97-99.

[8] 莫丰勇. 印染企业浸染生产排产优化问题研究及系统设计[D]. 杭州：浙江工业大学，2008.

[9] LAOBOONLUR P ，HODGSON T J，THONEY K A. Production scheduling in a knitted fabric dyeing and finishing process[J]. The Journal of The Textile Institute，2006，97（5）：391-399.

[10]PINEDO M L. Scheduling： Theory， algorithms， and systems [M]. 2nd ed. New Jersey，USA： Prentice-Hall Inc， 2001.