理解，数学教学的应然追寻

江苏徐州市铜山区黄集实验小学（221145）

《义务教育数学课程标准（2011年版）》指出：“课程内容的选择要贴近学生的实际，有利于学生体验与理解、思考与探索。”数学理解就是从生活经验表象中抽象出数学知识的过程，可以促进学生知识的迁移，让学生对知识做到“知其然且知其所以然”。那么，如何促进学生的数学理解，提升学生的思维品质呢？笔者从自身的教学实践出发，进行了积极的探索。

一、建立新知的基本模型，铺设数学理解的基石

皮亚杰指出：“数学知识是以一定的内在的逻辑组织起来的结构系统。”学生学习新知的过程，就是把新知与自身已有的知识经验进行对比，然后不断抽象、提炼，将其内化到自身的认知结构中的过程。在实际的数学学习中，学生更多会关注知识的局部散点状态，对数学知识的学习往往处于线性的积累状态，缺乏整体的把握。有的新旧知识之间的联系非常密切，旧知能自然生长出新知，新知又涵盖了旧知，知识的迁移自然而无痕迹；有的新旧知识之间的联系不紧密，恰处于知识的区分点，这类新知往往不易于学生理解。因此，教师应从学生的数学理解出发，关注知识之间的逻辑关系，从整体结构上引导学生建立新知的认知模式，促进学生深层次的数学理解。

如教学苏教版教材三年级“小数的初步认识”时，由于缺少相应的知识联系支撑，学生由整数的认识向小数的认识迁移时遇到困难。教师可先通过创设研究课桌的长和宽的长度的情境，揭示引入小数的必要性，感受一位小数与十分之几的联系，体会一位小数的含义；接着，引入生活中购物的情境，激活学生的日常生活经验，让学生在熟悉的商品价格的基础上认识小数，然后观察小数与以前学过的数的不同之处，形成“铅笔的价钱0.6元就是6角”的认知，并从元和角的进位关系理解零点几元的含义。通过“圆珠笔的价格是1元2角，就是1.2元”之类的问题，激活学生已有的生活经验，明确几元几角可以改成用“元”作单位的小数，明确“十分之几可以写成一位小数，一位小数表示十分之几”。通过丰富的生活经验建立促进学生理解的数学模型，不仅给学生的认知提供了起点和支撑点，还为学生进一步探究数学知识打下了知识基础和方法基础。

二、构建准确的知识表象，深入数学理解的核心

知识表象，就是学生对抽象的知识的直观感知，它具有概括性和可描述性。构建准确的知识表象，就能快速地回忆和提取，便于思维集中于问题解决的关键点，使学生的数学理解更有效。知识表象的构建，是一个不断深化、提升、纠正和精确的过程。在这个过程中，学生经历观察、操作、想象、思考，不断把生活经验表象化，促使思维逐渐走向深刻。

如教学苏教版教材四年级“三角形的认识”时，教师引导学生通过操作，体会三角形的特征，促使学生把隐性的认知建构为准确的知识表象。教师在方格纸中画出4个点（如下图），要求学生先选择3个点连成三角形，探究一共有多少种不同的方法，使学生的空间能力得到提升，然后思考可以去掉哪个点，使得剩下的3个点仍能连成三角形，让学生明白，构成三角形的3个点不能在同一条直线上，深化学生对三角形的认识。

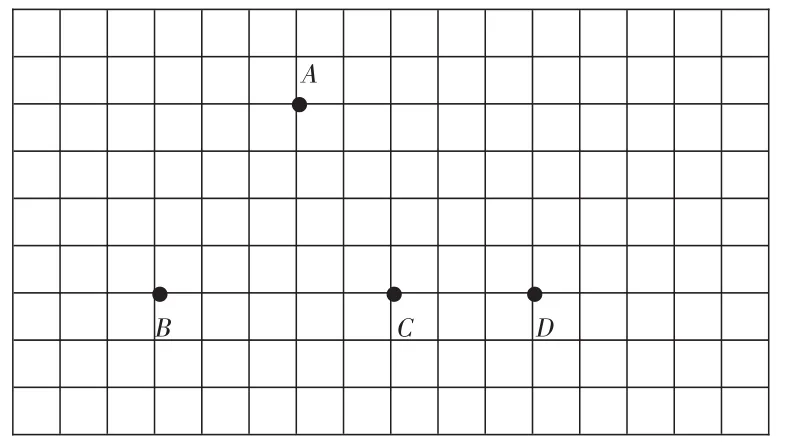
通过数学活动，让学生体验和感悟数学知识的形成过程，顺应了学生的思维，同时让学生建立起清晰的知识表象，使学生收获知识与技能。学生通过实验操作，深刻理解了知识的本质特征，提升了认知水平和数学思维品质。

三、着眼知识之间的联系，夯实数学理解的根本

数学学习，是把从外部获取的数学材料进行加工、整理，并内化到认知结构的过程。这个过程中，需要找到新知与原有知识之间的相同点和不同点，建立紧密的知识联系，才能形成良好的认知结构。教师应着眼知识之间的联系，从学生的认知实际出发，促使学生亲历知识的发生和发展过程，感悟其中的基本数学思想，积累活动经验，引领学生的思维发展。

如教学苏教版教材四年级“三角形三边的关系”时，教师先引导学生动手实践，让学生感悟到数学来源于生活，然后通过观察、分析、猜想、计算、比较、验证等数学活动，培养学生的空间观念、数学理解能力、合情推理能力以及抽象概括能力。

教师给每个小组（2人）提供了分别长3厘米、4厘米、5厘米和8厘米的小棒各1根，让学生用其中的3根围三角形。在交流时，教师让学生说出哪些小棒能围成三角形，哪些不能围成三角形。

生1：3厘米、4厘米和5厘米的小棒以及4厘米、5厘米和8厘米的小棒这两组小棒可以围成三角形，而3厘米、4厘米和8厘米这个组合的小棒不能围成三角形。

师：3厘米、5厘米和8厘米这组小棒能围成三角形吗？

（出示学生的围法，不能围成三角形）

师：为什么这组小棒不能围成三角形呢？

生2：其中两根小棒不能首尾相接。

师：看来3根小棒能不能围成三角形也是有条件的。仔细观察刚才的4组数据，你有什么发现？

（学生观察、交流，得出结论：三角形任意两边的和大于第三边）

教师从学生已有认识出发，让学生通过围三角形的活动获取直接的数学活动经验，培养了学生分析数据、推理和数形结合的意识。

四、组织合理的认知结构，促进数学理解的升华

数学知识的学习过程，就是学生组织、内化和完善认知结构的过程。随着活动体验的深入，学生的活动经验不断丰富，认知不断增多，需要进行认知结构的再组织。因此，教师要从学生的认知特点出发，顺应学生的思维，给予学生足够的时间和空间，让学生充分经历观察、分析、比较、验证等数学探究过程，使学生的认知由模糊走向清晰，由肤浅走向深入，由片面走向全面，认知结构不断趋向合理、丰满、完善。

如教学苏教版教材五年级“圆的认识”时，教师首先进行“你说我猜测”的游戏活动，出示长方形、平行四边形和圆这三种图形，要求描述时不能带有名称中的任何字词，发展学生用语言描述图形特征的能力。接着，创设“投球比赛”的情境，引导学生思考：为什么要围成圆形队伍？为什么把球筐放在中心位置才公平？这时，引领学生对正方形、长方形、圆进行对比，直观得出将球筐放在圆形队伍的中心位置，每个人到中心的距离都相等，这样比赛才公平，然后在此基础上，把研究的对象引向圆的本质特征——一中同长。最后，通过画圆和折圆的活动，进一步探究圆心、半径和直径的相关知识。这个环节层层递进，符合学生的认知特点，逐步引导学生组织合理的认知结构，由新知向旧知过渡，不断加深学生的数学理解，使学生的数学思维品质不断提升。

综上所述，数学理解是动态的发展过程。在数学课堂教学中，教师应基于学生已有的认知水平和知识经验，创设具有启发性的问题情境，让学生亲历知识的形成过程，顺应学生的思维，促进学生的数学理解，发展学生的数学智慧。