复杂约束条件下求解带权最短路径方法

杨 澜，段卓辉，邓宏涛*

（1.江汉大学 数学与计算机科学学院，湖北 武汉 430056；2.华中科技大学服务计算技术与系统教育部重点实验室/集群与网格计算湖北省重点实验室，湖北 武汉 430074）

0 引言

随着硬件条件的不断发展和RDMA、SDN、NFV技术的不断完善，网络拓扑变得越来越复杂，网络环境也变得更加复杂。在复杂的环境下，寻找带权最短路径成为一大挑战。传统的搜索算法并不能较好适应复杂的网络环境，回溯算法［1］、深度优先算法［2］、A*算法［3］都无法解决复杂约束条件下的带权最短路径问题，繁杂的约束条件破坏了深度遍历或广度遍历求解带权最短路径的可能，多约束条件下求解带权最短路径成为NP难问题。

为了解决复杂约束条件下带权最短路径问题，已有研究基于传统的Dijkstra算法、Floyed算法和A*算法实现了定路径规划的优化算法［4-6］。虽然这些研究尝试在约束条件下解决带权最短路径问题，但条件建模多偏向于路径权值变化的单一约束。基于稳定分支的变权网络最优路径算法［4］优化了Dijks⁃tra算法并设计稳定树算法动态调整权值路径，使其最短权值路径保持稳定，但真实网络的约束条件不仅只有权值变化。基于复杂权值优化的A*路径搜索算法［5-6］也是侧重于适应复杂权值变化，并通过优化A*算法求解带权最短路径问题。但该算法与变权网络最优路径算法存在相同的问题，并不能求解出复杂约束条件下最优的带权最短路径可行解。

传统的带权最短路径算法已经可以在较小时间复杂度内求出最优解，如SPFA算法［7］等，但当带权最短路径问题遇到复杂的约束条件，权值最小的贪心思想将不再适用，每次路径的选择需严格满足约束条件，问题规模从较小复杂度转化成NP难。最直观的解决思想就是遍历所有路径，查找其满足约束条件路径的最小值。虽然这种思路直接明了并能求出精确解，但随着计算规模增大，其耗时较高。

剪枝可以减小图规模，剔除显然不满足约束条件的遍历路径从而减小遍历开销。剪枝遍历算法虽然可以解决复杂条件下的带权最短路径问题，但其算法复杂度还是随着图规模的变大而急速增加。虽然存在动态剪枝等［8-9］优化策略，但其求解的时间复杂度还是过于庞大。启发性算法虽能解决复杂约束条件下的带权最短路径问题，如PSO算法［10］、蚁群算法［11］、遗传退火算法［12］等，但其求解迭代耗时较高，启发路线复杂，自学习不稳定，极易陷入局部最优的情况。这类算法并不适合直接用于求解复杂约束条件下带权最短路径问题。

本文将复杂网络环境中的约束条件抽象成几类传统图中约束条件组合，同时将实时网络转化为多种约束的抽象图。在考虑权值、顶点约束和边约束的情况下解决带权最短路径问题。本文提出基于压缩图的禁忌搜索算法，通过考虑多种约束条件来对求解图进行压缩，并利用优化禁忌搜索算法求解带权最短路径。

1 问题描述和网络建模

为解决复杂网络环境下带权最短路径问题，首先需要对复杂网络环境中的约束条件进行建模，将复杂网络环境转化为带约束条件的图数据结构。将网络约束条件转化为图的约束条件组合后即可利用优化搜索算法解决复杂约束条件下带权最短路径问题。

通过对网络环境中可能存在的一些复杂约束情况进行分析，将其与图中约束条件对应组合进行建模。由此，约束可分为以下4类：必须经过的边；必须经过的顶点；不能经过的边；不能超过的最大跳数。利用上述4种基本约束类可以组合成各种复杂的网络环境约束条件。下面通过这4种抽象约束条件类对几类常见的网络环境情况进行分析：

1）服务点损坏：因为长时间工作，很可能导致网络中某服务点产生异常。基于约束类可将此抽象为与该服务点链接的所有边都不可达，这样就可以在原有的网络拓扑图中将损坏服务点剔除。

2）网络拥塞：网络拥塞是一个非常复杂的情况，基于约束类可通过不能经过的边加上必须经过的边和顶点来模拟网络协议中对拥塞情况下做出的妥协，并可以利用更新约束条件来形成当前环境下的新网络拓扑。

3）信号衰减：基于约束类利用最大跳数来限制数据路由能通过的节点个数（路由器）。并通过必须经过的节点（信号放大器）来实现长距离传输。

综上所述，此类约束条件所组合的抽象类确实能在一定程度上含括复杂网络环境中的约束。通过利用基础约束条件抽象类适当搭配所形成的约束组合，能将复杂网络环境转化为多种约束条件的传统图。

2 算法设计和实现

在对NP难图算法问题的研究中，图的规模大小是影响求解NP难问题的重要因素。图划分通过图压缩提升寻找最短路径的效率［13］。虽然剪枝算法能在一定程度上压缩图规模，但其压缩过程是在DFS遍历过程中进行，实际上并不能有效降低图规模。本文提出了一种针对复杂约束条件的图压缩算法，并介绍了基于图压缩的禁忌搜索算法。

图压缩算法的具体步骤如下（原图中的点为顶点，压缩图中的点为节点）：

1）选取原图中的必过顶点、起点、终点作为压缩图的节点。

2）利用SPFA算法计算原图中满足最大跳数的任意两点之间的最短路径权值，并记录其对应跳数和路径。

3）取压缩图中的任意两节点，并取步骤2）中所算出的原图中此两点的最短路径权值和作为压缩图此两点边上的权值，反复这一步骤直到压缩图形成完全图。

4）找到原图中必过边对应的顶点，并将这两顶点在压缩图中的边权值赋值为必过边权值，并改动步骤2）中记录下来的最短路径权值、对应跳数和路径。

压缩图必定包含约束条件中的必定经过顶点。在新构造的压缩图中，只存放起点、终点、必须经过顶点。之后利用SPFA算法计算新构造的压缩图中任意两点在原图中的带权最短路径，将计算出来的值记为新压缩图中边的权值。同时记录压缩图节点间在原图中的最短路径和跳数。压缩图减少了顶点数量，只保留必须经过顶点，减少了图规模。此时压缩过的完全图中所有边的权值为原图中顶点间最短路径权值。

如图1所示，顶点0到3间存在必过边，顶点3为必过顶点，起点为0，终点为5。若使用上述方法进行压缩则可能去掉必过约束边。因此，在压缩过程中，如果存在必过边，那么这两个顶点间的最短路径为必过边，权值为必过边权值（见图2）。

图1 实例原图Fig.1 Example graph

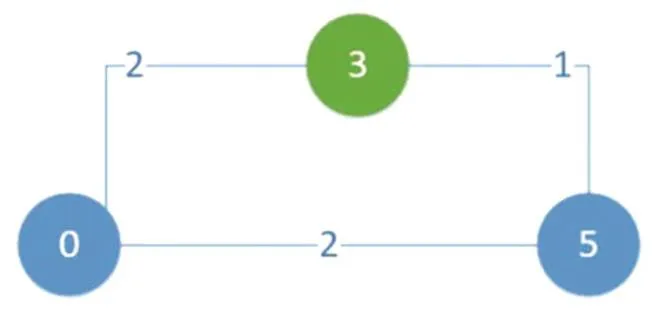
图2 最终压缩图Fig.2 Final compression graph

在图压缩算法中，SPFA以权重优先查找最短路径［14］，这会舍去跳数低的高权值路线，从而因不满足跳数约束条件导致无解。笔者在图压缩算法查找最短路径的SPFA中加入了最大跳数约束，避免在图压缩过程中失去可行解。

虽然图压缩算法缩小了原图规模，但因压缩图是一个由必过节点组成的完全图，其图复杂程度和必过节点数息息相关。如果当约束条件中必过顶点个数较多时，压缩图规模还是会较大，若此时使用剪枝DFS算法求解，则依旧是NP难问题。所以为了避免这种情况的发生，本文使用禁忌搜索算法对压缩图的带权最短路径进行求解。

因压缩图是由必过顶点组成的完全图，所以压缩图上的单源最短路径（single-source shortest path，SSSP）问题就被转化为了旅行家问题（traveling salesman problem，TSP）［15］。通过设计禁忌搜索算法（Tabu search algorithm）以适应压缩后图规模依旧过大的特殊情况。

在禁忌搜索算法中，首先按照随机方法产生一个初始解作为当前解，随后在当前解的邻域中搜索若干个解，取其中的最优解作为新的当前解。为了避免陷入局部最优解，算法允许一定的下山操作，使解的质量变差从而激活搜索，以偏向全局最优解。另外，为了避免对已搜索过的局部最优解重复搜索，本算法使用禁忌表记录已搜索的局部最优解历史信息，从而使搜索过程避开局部极值点，从而开辟新的搜索区域。

在搜索中构造一个短期循环记忆禁忌表，禁忌表中存放刚刚进行过的T（T为禁忌表长度）个邻居的移动，这种移动即解的简单变化。禁忌表中的移动称为禁忌移动。对于进入禁忌表中的移动，在以后的T次循环内是禁止的，以避免回到原来的解，从而避免陷入死循环。T次循环后禁忌解除。禁忌表是一个循环表，在搜索过程中被循环修改，使禁忌表始终保持T个移动。即使引入了禁忌表，禁忌搜索仍可能出现循环。当迭代内所发现的最好解无法改进或无法离开它时，算法停止。

3 测试评估

实验的硬件测试环境：CPU为主频2.6 GHz的20核Intel（R）Xeon（R）CPU E5-2670，内存大小64 GB。实验采用CentOS 7系统，内核版本为4.7.0。

测试案例使用中兴提供（http://challenge.zte.net/activity.php?mod=info#title2）的网络测试案例拓扑，如图3所示。绿色节点为必须经过顶点，绿色边为必须经过边，红色边为无法通过边。对DFS剪枝、压缩图剪枝、压缩图禁忌搜索算法进行测试。

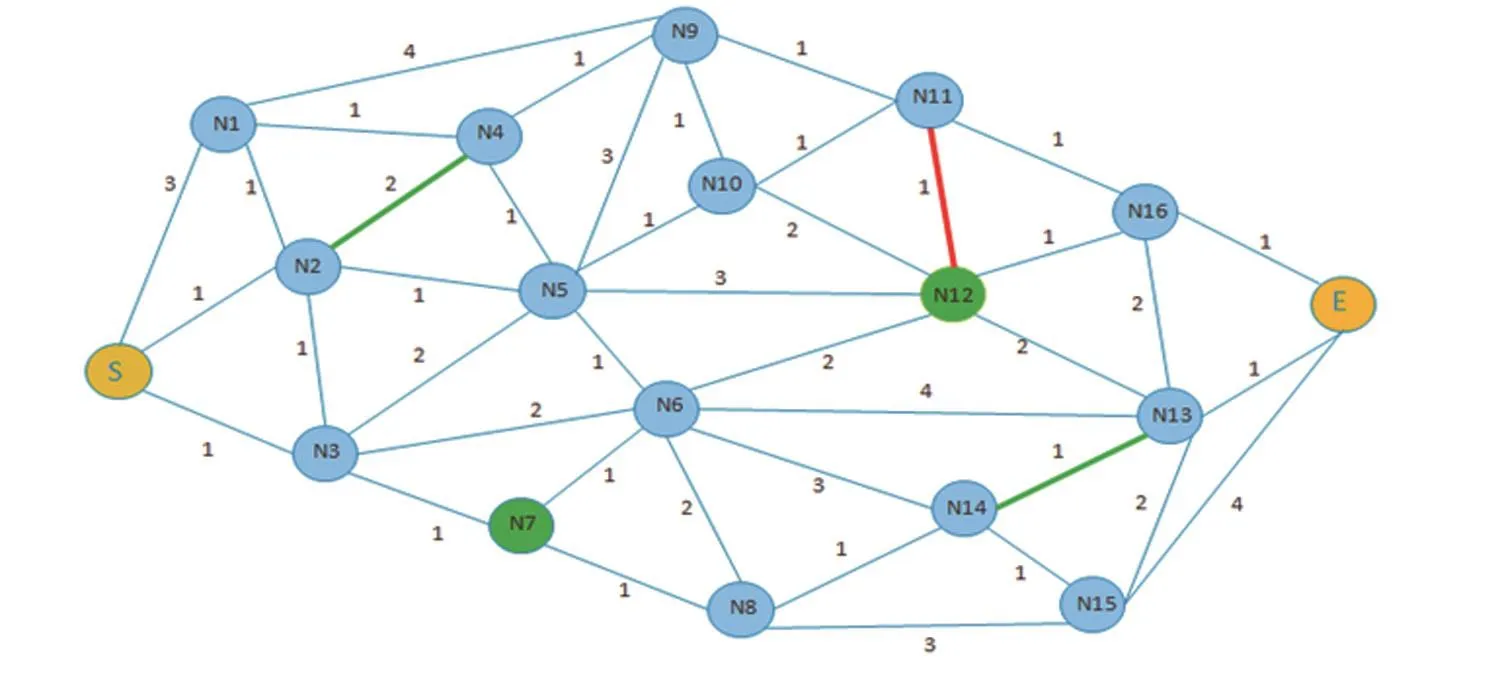
图3 中兴网络测试拓扑Fig.3 Topology of ZTE network test

3.1 算法对最大跳数约束条件的敏感性

通过运用控制变量法将约束边、约束顶点保持不变，并调整同一案例上允许的最大跳数来测试算法运行时间。在中兴网络测试拓扑上，分别设置最大跳数为11、12、13、14跳，并测试各算法的运行时间，结果如图4所示。

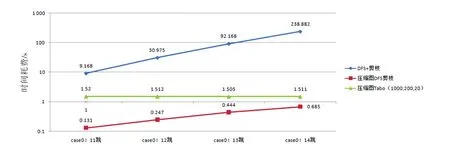
图4 算法测试结果Fig.4 Results of the algorithm test

从实验结果可以看出，DFS剪枝算法对最大跳数约束是敏感的，不论是在原图还是压缩图，其运行时间都随最大跳数增加而增加。当约束条件规模变大时，其性能将会变差。从图4中可以发现，基于压缩图的DFS剪枝性能要大幅优于原图DFS剪枝，这说明图压缩算法起到了化简图的作用，并大大提高了DFS剪枝算法的性能。而压缩图禁忌搜索算法对最大跳数不敏感，当图规模变大，其运行时间不会明显增加，并且耗时远小于DFS剪枝。这说明压缩图禁忌搜索算法并不会因为约束条件规模增大而性能变差。

3.2 图规模对算法性能的影响

为了探究算法性能优化是否会因图规模大小而不同，控制最大跳数不变，观察图规模变化对算法的影响。为了满足测试需要，笔者构建了相同约束数量，不同图规模的测试用例数据见表1。

表1 不同规模图用例表Tab.1 Cases table of different size graphs

设定最大跳数为11跳，并记录不同算法对应的运行时间，结果如图5所示。DFS剪枝算法和压缩图DFS剪枝算法整体上对图规模敏感，虽耗时呈现线性上涨的趋势，但存在明显波动。笔者分析了这些波动点（DFS剪枝在case 1、case 3、case 5上约束11跳和压缩图DFS剪枝在case 1上约束11跳），在case 3和case 5上设置约束跳为12跳进行重复实验，此时运行时间恢复正常增加趋势。由于case 1、case 3和case 5用例上存在一个11跳的无解空间，导致DFS在深度遍历的情况下找不到11跳的满足条件，提前剪枝，大大收缩了图规模，从而导致敏感性波动。但从整体趋势来说，DFS剪枝算法、压缩图DFS剪枝算法都对图规模敏感，并随着图规模的增加使得运行时间增加，这说明DFS算法不能适用于大规模图的求解。而压缩图禁忌搜索算法对图规模并不敏感，并且能在较小耗时求解。这说明了压缩图禁忌搜索算法能较好求解具有约束条件的大规模图。

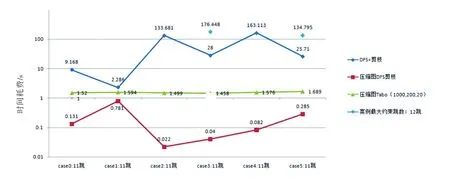
图5 最大跳数11情况下图规模敏感性实验图Fig.5 Figure scale sensitivity test with maximum hops 11

4 结语

文本旨在解决复杂网络环境下求解带权最短路径（开销最短路径）问题，并提出了基于压缩图的禁忌搜索算法。通过图压缩算法，将复杂约束条件下的带权最短路径问题转化为旅行家问题（TSP），再通过优化禁忌搜索算法求解复杂约束条件下带权最短路径问题。实验结果表明，基于压缩图的禁忌搜索算法具有求解快、时间复杂度低、收敛快、对图规模和约束条件不敏感的优点。在后续研究中，笔者将致力于优化基于压缩图的禁忌搜索算法在稀疏图上的性能，并考虑加入图划分的并行禁忌搜索算法以解决超大规模图的问题。