具有可选服务和负顾客的M/G/1/N可修排队系统
2018-09-05高显彩单雪红
高显彩,单雪红
(宿州学院 数学与统计学院,安徽 宿州 234000)
0 引言
许多学者都对负顾客排队模型都作了大量研究[1]-[4].文[5]研究了带负顾客的M/G/1重试可修排队系统,文[6]研究了具有优先权的M/G/1重试可修排队系统,文[7]研究了有可选到达、服务台可修的M/G/1重试可修排队系统.本文在此基础上研究具有可选服务和负顾客的M/G/1/N可修排队系统,利用补充变量法和状态转移分析模型,得到了瞬态队长分布及稳态队长分布的相关排队指标.
1 模型描述

(2)系统容量有限.若N个服务台全部工作时,则刚到的正顾客就会离去;若有空闲的服务台,则刚到的正顾客进入系统等待服务.如果服务台发生故障,需修理,顾客或等待服务台修理好后继续接受服务,或自动离开,服务台修好后正常工作.
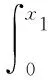
2 系统状态及其概率定义
设N(t)为t时刻系统中的正顾客数, {N(t)|t≥0}不是Markov过程.引入补充变量X1,2(t),表示正顾客在t时刻已接受的必选服务和可选服务的时间.


则{N(t),S(t),I(t),X1,2(t)|t≥0}是马尔可夫过程.

定义P(k,j,i,t)=P{N(t)=k,S(t)=j,I(t)=i}(k=0,1,2,…N;j=0,1,2;i=0,1)
P(k,j,i,x,t)dx=P{N(t)=k,S(t)=j,I(t)=i,x 初始条件:假定开始时系统处于空闲状态,且有P(0,0,1,0)=1 通过分析得偏微分方程组: (1) (2) (3) (4) (5) (6) 边界条件: (7) (8) (9) (10) 对(1)~(10) 式取L变换并解方程组得到: (11) (12) (13) (14) (15) (16) (17) (18) (19) 定理1 瞬态队长分布的L-Z变换 (20) 定理2 稳态队长分布的广义概率母函数 (21) 证明:由L变换的终值定理和式(20)得: 本文研究具有可选服务和负顾客的M/G/1/N可修排队系统,利用补充变量法、状态转移分析法,得到了瞬态队长分布的L-Z变换、稳态队长分布的概率母函数.3 建立模型方程与求解




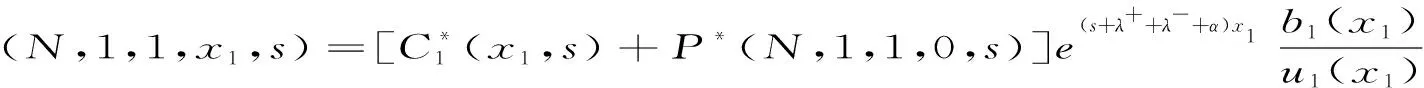








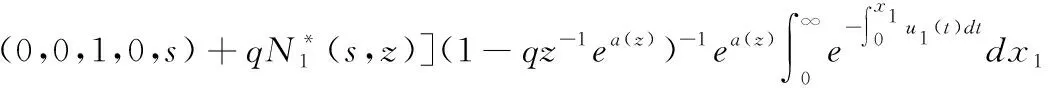


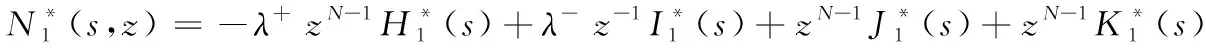

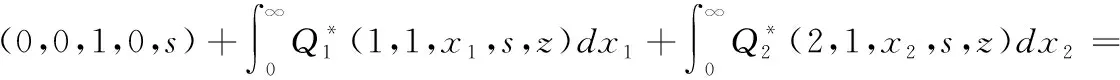
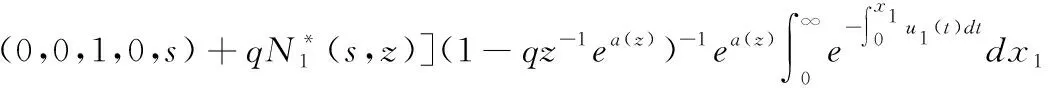



4 结论
