不完全信息下基于证据推理的直觉模糊多属性决策方法
2018-09-04刘文清王应明蓝以信
刘文清,王应明,蓝以信
(福州大学 决策科学研究所,福州 350116)
0 引言
直觉模糊集(IFS)[1]是Atanassov于1983年提出的概念,是对模糊集概念的拓展,由隶属度、非隶属度和犹豫度(未知度)三方面组成。因此IFS在表达模糊性和不确定性等方面具有更优秀的灵活性和实用性,直觉模糊多属性决策也成为当前决策领域的一个研究热点[2]。近年来关于直觉模糊集在多属性决策上的方法研究层出不穷,并广泛地应用于专家系统、医疗诊断、模式识别、决策分析等众多领域[3]。
在实际决策中,存在着大量属性值信息不完全的问题,因此针对属性值信息不完全的直觉模糊多属性决策问题有着很强的现实意义。由于众多直觉模糊信息集成的方法都只能应用在属性值信息完全的情况下,因此目前在处理属性值信息不完全时,一般都是用直觉模糊相似度函数等方法先将属性值补全,使之变成信息完全的直觉模糊多属性决策问题。但是补全信息等于丢失了此类直觉模糊多属性决策问题中信息不完全这一特性和信息,同时当数据量较大且缺失数据较多时,其计算量会非常大。
证据推理是对证据理论的发展,Wang等[4]提出的ER组合方法解决了证据理论中Dempster组合规则融合证据时造成的证据冲突问题,在不确定决策和不完全信息多属性决策上有着广泛应用。张洪涛等[5]用证据推理方法将属性值信息不完全的多个专家意见进行集结,并应用于汽车企业自主创新能力的评价中。施海柳等[6]在并购决策中利用证据推理来集结有数据缺失的多时点投入产出信息。
为此,本文针对目前方法在属性值信息不完全的直觉模糊多属性决策问题上的不足,提出了不完全信息下基于证据推理的直觉模糊多属性决策方法,利用证据推理可以处理不完全信息和不确定信息的特点,在集成直觉模糊信息时得到的结果依然为直觉模糊数,以免造成信息的丢失,还可以保留信息不完全这一信息,并且省去了补全信息的繁琐。最后算例分析验证了本文方法的有效性和可行性。
1 基本理论
1.1 直觉模糊集相关理论
定义1[7]:设B为论域E上的一个直觉模糊集,则B定义为如下形式:

其中 μ(x)为元素 x∈E 属于 B的隶属度,v(x)为元素x∈E属于B的非隶属度,并且满足以下条件:

显然,直觉模糊集作为模糊集的一般化,每个传统模糊集都可以写成如下形式:

定义2[7]:对任意的 x∈E 有 πB(x)=1-μB(x)-vB(x),称为元素x为直觉模糊集B的犹豫度或未知度。显然,对传统模糊集来说,对任意的x∈E都有πB(x)=0。
E中的元素x属于B的隶属度与非隶属度所组成的有序对 μB(x),vB(x)称为直觉模糊数。
1.2 证据推理基本概念
定义3[8]:H={H1,H2,…,HP} 为证据的识别框架,H1,H2,…,Hp表示定性值 Y1,Y2,…,Yp对应评价等级,HN⊆H 表示未知信息,(Hk,βk)表示在等级 Hk的置信度为 βk,(HN,βN)表示关于未知信息 HN的置信度为 βN,则称 βk为Hk上的等级置信度,βN为HN上的等级置信度,其中

定义 4[9]:H={H1,H2,…,HP} 为识别框架,若集函数
m∶2H→[0,1] 满足≤1,称m为H上的基本可信度分配(BPA)。
2 不完全信息下基于证据推理的直觉模糊多属性决策模型
2.1 问题描述
假设一个直觉模糊多属性决策问题有l个备选方案和n个评价属性,令S={s1,…,si,…,sl}表示方案集 ,A={A1,…,Aj,…,An} 表示为属性集,对应属性的权重为W={ω1,…,ωj,…,ωn} ,满足
方案 si在属性 Aj下的直觉模糊评价值为μj(si),vj(si),对应的未知度为 πj(si)=1-μj(si)-vj(si),1≤i≤l,1≤j≤n 。则有如下直觉模糊决策矩阵:

2.2 属性值信息缺失的处理
当属性值缺失为空时,说明此时可获得信息为零,此属性值是完全未知的,因此其隶属度和非隶属度应为0,未知度为1。若将隶属度和非隶属度补齐为非零数字,则未知度π≠1,表明此属性值信息并不是完全未知,而是可知的,这与属性值缺失的本身含义不符,因此有如下定义。
定义5:当属性值缺失时,则赋值为 0,0,即隶属度u=0,非隶属度v=0,未知度π=1。
采用定义5来处理属性值缺失不仅简单,并且可以保留信息缺失这一信息,更加合理。
2.3 直觉模糊信息的处理
证据推理在融合不确定信息有着广泛应用,但是并不能直接处理直觉模糊信息,因此需要将直觉模糊信息转化为证据推理可以处理的等级置信度。
通过比较直觉模糊集的定义与定义3可以看出,直觉模糊集与等级置信度有着相似之处,HN表示未知信息,而π表示未知程度,因此有如下定义。
定义6:设 H={H1,H2}为属性的识别框架,等级H1表示隶属度,等级H2表示非隶属度,HN⊆H表示未知度。则(H1,μ)表示在等级H1的置信度为μ,(H2,ν)表示在等级H2的置信度为 ν,(HN,π)表示关于未知度HN的置信度为π,简记为 μ,ν,其中μ+ν+π=1。
按定义6将属性值的直觉模糊信息看作为等级置信度信息,则可用证据推理来对直觉模糊信息进行集成。
2.4 基于证据推理的直觉模糊信息集结
证据推理在多属性决策问题中的应用是将各属性看作证据,属性值则为证据的具体值,则基于证据推理的直觉模糊信息集结方法如下:

其中 1 ≤i≤l ,1 ≤j≤n ,m1j(si)+m2j(si)+mNj(si)=1 。由上述公式计算可以得到BPA决策矩阵,表示如下:

其中 m1j(si)为方案 si在属性 Aj关于等级 H1的BPA,m2j(si)为方案 si在属性 Aj关于等级 H2的BPA,mNj(si)为方案si在属性Aj关于未知度HN的BPA。
第二步:将BPA决策矩阵用ER方法进行集结,集结公式如下:

其中 k=1,2,1≤i≤l,1≤j≤n。则可以得到方案 si总的BPA值:m1(si),m2(si),͂N(si),mˉN(si)。
第三步:计算方案si总的直觉模糊评价信息。由方案总的BPA计算得到方案总的直觉模糊评价信息,如下:

2.5 直觉模糊数的排序比较
在现实决策环境中,对直觉模糊数的比较和排序是非常重要的一个问题,同时也是决策过程中重要的一步。这里采用了谭吉玉等[3]提出的相对于最大直觉模糊数的贴近度来进行排序,其不仅蕴含了得分函数和精确函数的排序原理,而且克服了在排序时得分函数处于绝对优势地位的不足。相对于最大直觉模糊数的贴近度计算公式如下:

按照C(si)值的大小对方案进行排序 (i= 1 ,2,…,l) ,C值越大,方案越优。
3 算例分析
在信息化条件下进攻战斗中,敌方利用其火力打击我陆军地面进攻部队,致使我方进攻受阻,严重影响了我方作战计划的实施。为能争取战场主动控制权,上级命令对该区域实施火力打击,破坏敌防御系统。我某数字化师利用先进的侦察系统获取了该地区的目标情报,制定了三种不同的火力打击行动方案现有5位相关领域的战略战术专家DM1、DM2、DM3、DM4、DM5对这3种方案依据其评价指标做出评价信息,如表1至表5所示:
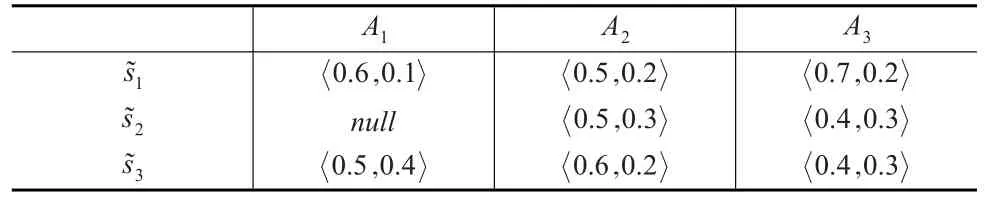
表1 专家DM1对敌作战体系毁伤评估
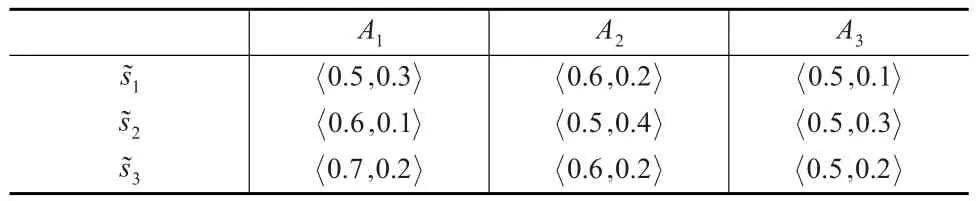
表2 专家DM2对敌作战体系毁伤评估

表3 专家DM3对敌作战体系毁伤评估

表4 专家DM4对敌作战体系毁伤评估

表5 专家DM5对敌作战体系毁伤评估
属性权重则为 ω1=(0.3,0.3,0.4),由于各个专家的重要性相等,因此假设各专家权重相等 ω2=(0.2,0.2,0.2,0.2,0.2)。
可以看到评价信息有几处缺失,是属性值信息不完全的直觉模糊多属性决策问题。由于有五位专家分别对三个方案做出评价,同时也是多属性决策中的群决策问题。
首先将其看作5个多属性决策子问题,对5个子问题分别用基于证据推理的直觉模糊信息集结方法来得到每位专家对3种方案总的评价值,如表6所示:
然后将决策表表6看做一个多属性决策问题,专家可以看作为属性,再用基于证据推理的直觉模糊信息集结方法得到各方案总的直觉模糊评价值,最后进行排序比较,选出最优方案。将本文方法结果与文献[10]的结果进行比较,见表7:

表6 各专家对3种方案总的评价值

表7 文献[10]方法与本文方法结果对比
从表7可以看出本文方法与文献[10]结果差别在于方案1与方案3的排序不同,出现这种情况的原因是文献[10]是用IFWA算子来集结直觉模糊信息。由于方案͂3的评价值中存在极端数据即非隶属度为0的情况,而IFWA算子在遇到非隶属度为0的直觉模糊数时其计算得到的直觉模糊数的非隶属度必为0。因此通过IFWA算子计算得到方案͂3的总的直觉模糊评价值非隶属度必为0,这样就导致方案͂3的评估不合理。
用基于证据推理的直觉模糊信息集结法来计算文献[10]中补齐后的直觉模糊评估信息,所得结果为͂=〈0.7531,这与本文所得排序结果相同,说明本文方法在遇到直觉模糊评估信息缺失时所得结果是合理的,表明本文方法可以有效地解决属性值信息不完全的直觉模糊多属性决策问题。
4 结论
在实际的直觉模糊多属性决策问题中,由于各种原因会导致属性值信息的缺失,现有的直觉模糊信息集成方法并不能直接有效地处理这类问题。本文提出了不完全信息下基于证据推理的直觉模糊多属性决策方法。该方法定义了如何用直觉模糊数来表示属性值的缺失,简单合理易懂,免去了补齐数据这一步骤,同时保留了数据缺失这一信息。通过分析直觉模糊集与证据推理之间的相似性将直觉模糊集中的隶属度、非隶属度和未知度转化为证据推理中的等级置信度,由等级置信度得到BPA后用ER组合方法来集结信息,最后计算各方案总评估值的贴近度来进行方案排序。算例分析验证了所提方法的有效性和可行性,为属性值信息不完全的直觉模糊多属性决策问题提供了新的途径,具有一定的应用意义。
