含柔性负荷的主动配电网优化模型研究*
2018-09-03贾先平邹晓松袁旭峰熊炜
贾先平, 邹晓松, 袁旭峰, 熊炜
(贵州大学 电气工程学院,贵阳 550025)
0 引 言
近年来,柔性负荷成为了学术研究的重点,柔性负荷的调度和调节是缓解供需侧矛盾的重要手段之一。柔性负荷的柔性调节能力改变了原本负荷单向、被动接受调节的历史,也使负荷参数的刚性、不确定性等特征发生了变化。另外电动汽车、分布式电源的接入使负荷具有了一定电源的作用。随着并入电网的分布式电源越来越多、电动汽车和储能元件等柔性负荷的大量增加和普及[1],使得配电网优化调度研究成为一个面临巨大挑战的课题,需要综合考虑能耗、网损和大量接入的分布式新能源[2]。主动配电网的优化调度引入柔性负荷能够积极消纳间歇式新能源、削峰填谷,有利于丰富电网调度运行的调度手段[3-4]。文献[5]研究柔性负荷的控制框架与策略,考虑了馈线控制和电力客户两方面的利益,基于混合系统模型提出柔性负荷信息物理融合的控制模型与方法,对柔性负荷合理的调度实现系统运行经济性。
主动配电网(ADN)[6]优化调度的建模有分时段调度、多目标协调优化等的优化调度方法策略,二层规划模型是多层规划模型中的一种特殊情况[7]。上层模型与下层模型之间有着内在的联系,上下层模型有各自的目标函数和约束条件,下层模型作为上层模型的约束,二者相互制约、相互影响[8]。文献[9]将完整的调度周期分为日前24 h负荷调度、日内1 h符合调度、日内15 min负荷调度和实时负荷调度4个时间尺度建立多时间尺度的柔性负荷互动响应调度模型,设计了“多级协调、逐步细化”的调度策略,提高系统调度的经济性。文献[10]考虑了储能和柔性负荷的时空联系与网络潮流的影响,建立一可再生能源利用率最大、网络损耗最小和用户满意度最高的主动配电网多目标优化调度模型,通过设定可控分布式发电单元、储能系统及柔性负荷的调度有限级量化的ADN各单元间的协调作用,积极消纳可再生能源,有效的减少网络有功损耗,提高用户满意度。文献[11]不仅考虑到ADN内部安全运行又考虑到多竞争者参与的电力市场出清,基于随机规划提出一种ADN策略竞价的二层模型,以ADN的收益最大化为上层模型的优化目标函数,以社会效益最大化为下层模型的目标函数,基于互补理论将二层规划模型转化为单层规划模型求解,即能够充分接纳ADN内部可再生资源,调动柔性负荷,又能使ADN安全运行实现最大化经济效益。二层优化问题尤其适合多目标函数优化问题,各个目标函数之间存在着相互影响的关系,二层规划利用这种关系,结合决策变量的特点将系统分为2层,上层目标函数为总目标函数,根据该层的决策变量、可行域等做出决策;下层目标函数为上层目标函数决策的一部分,受到上层模型的制约,各个目标函数根据自己的目标函数调整自己的决策变量,获得目标函数最大化。
在多时间维度、多目标协调优化调度模型的建立中引入储能、分布式发电单元、柔性负荷都体现出了主动配电网优化调度关键技术的不断发展。文中结合含有柔性负荷的主动配电网的特点模拟一个典型ADN馈线系统,系统含有分布式DG单元、常规负荷和柔性负荷(可转移负荷和可中断负荷)。针对模拟的馈线系统建立二层优化调度模型,上层模型以ADN系统运行费用最低为目标函数,下层模型以微网区域运费费用最低作为目标函数,上层模型选择遗传算法求解,下层模型选择模拟退火算法求解,并给出算法求解流程。
1 柔性负荷
柔性负荷优化调度是主动配电网未来发展的潜在发展趋势和研究方向。柔性负荷就是具有柔性特征的负荷,这种负荷是灵活可变可调节的负荷。含柔性负荷的主动配电网优化调度考虑将调度灵活的负荷资源作为调度对象,采用适当的需求响应措施,实现柔性负荷与电源之间的源-荷互动响应,达到积极消纳间歇式新能源优化资源配置的目的。柔性负荷常用的调度模式包括基于电价的模式、基于合同约定的模式、需求竞价模式等。柔性负荷的分类从用户自主响应特性可以将柔性负荷分为可转移负荷、可平移负荷和可削减负荷三种类型[12]。按照对电价的敏感程度可以将柔性负荷分为可转移负荷和可削减负荷两种类型[13]。文中将柔性负荷分为可转移负荷和可中断负荷两个种类。
(1)可转移负荷出于对电价的考虑可以将用电行为从电价较高的时刻转移到电价较低的其他时刻,但是该用电行为仍然会发生,例如工厂生产用电、居民洗衣用电等等,可转移负荷虽然对电价比较敏感但是在一定的用电周期内总的用电量是保持固定不变的。具体表示如下:
PFLsh=PFLsh(λt)
(1)
式中PFLsh表示为柔性负荷的可转移量,即可转移负荷;λt表示为t时刻的实时电价
(2)可中断负荷对电价敏感,但其用电行为具有较大的灵活性,当其电价过高时可以减少直至取消用电行为,并且不再另外的时间段继续该用电行为,例如空调用电、娱乐用电等。具体表示如下:
式中PFLin表示柔性负荷可中断量,即可中断负荷;λM表示用户对电价敏感的临界价格。当电价低于λM时,用电行为不受电价的影响;当电价高于λM时,用户的用电行为是电价的函数。
2 二层数学模型
二层规划模型具有鲜明的层次性,上层模型和下层模型之间密切结合、相互制约,但是下层模型具有上层模型决策控制允许的范围内的自主权[12]。智能电网的迅速发展使得主动配电网的优化调度更趋向于多目标的优化,二层规划模型的鲜明的层次性正好可以满足多目标的优化问题,将优化模型分为上层模型和下层模型[13]。文中所述的二层规划模型中上层规划模型以主动配电网运行成本最低为目标函数,约束条件包括节点电压约束,支路潮流约束、节点功率平衡约束、线路出口功率上下限约等;下层模型以各个微网区域运行费用最少为目标函数,约束条件包括区域功率平衡约束、分布式单元发电功率上下限约束,柔性负荷上下限约束等。上层规划模型制约下层模型,下层模型作为上层模型的约束独立存在。
典型的ADN系统如图1所示,包含了四个降压变压器、四个不同电压等级的分布式DG发电单元和三个微网区域,并且以此系统为例建立二层优化调度模型。

图1 含有柔性负荷的ADN简易馈线系统Fig.1 ADN feeder system with flexible load
上层模型:
minC=CG1-CD1+CDG1+Cposs1+∑F
(4)
(7)

(14)
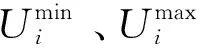
下层模型:
∑F=minF1+minF2+minF3
(17)
(21)


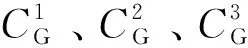
3 求解算法
3.1 算法简介
遗传算法是模拟生物进化过程的空间搜索算法,通过模拟生物进化自然选择和遗传过程中发生的繁殖、交叉和基因突变现象迭代产生新的种群,按照某种机理筛选出最有个体作为下一代遗传算子组合的对象,得到最优种群的智能优化算法[14-16]。遗传算法能够在约束条件较少的情况下面向全局寻找潮流计算的最优解,算法的稳定性较高,能够广泛运用到配电网的优化调度中求解最优方案[17]。模拟退火算法是基于概率的一种算法,是一种随机搜索算法,是通过赋予搜索过程一种时变且最终趋于零的概率突跳性,从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法[18]。由于二层规划本身具有很强的层次性,如果上下两层模型均采用遗传算法的话求解过程会变得相当复杂,因而文中结合遗传算法和模拟退火算法的特点构建一个混和计算模型来求解所提出的二层规划模型。
3.2 求解步骤
混合算法求解流程如图2所示。
(1)给定网络初始数据;
(2)形成节点的导纳矩阵Y及迭代的雅可比矩阵B;
(3)输入节点已知数据,通过求解潮流方程,得到上层关于遗传算法的初始群体,形成初始可行解空间,设定初始解为X0;
(a)根据初始可行解空间,利用模拟退火算法,选定初始温度T0,马氏链长度L0,温度衰减因子ΔT,终止温度Tfinal;

图2 混合算法求解流程Fig.2 Hybrid algorithm to solve the process
(b)产生一次随机的扰动,产生新的可行解空间,得到一个新解Xk;
(c)根据Metropolis准则判断是否接受新解,若新解的函数值小于或等于初始值的函数值,则接受新解,子代个体替换父代个体进入下一代;若新解函数值大于初始值函数值,如果依概率接受新解,则子代个体替换父代个体进入下一代;
(d)判断是否满足停止准则Tk (4)在步骤(3)输出的下层模型最优解的基础上对上层模型求解,利用遗传算法依据遗传算子(选择、交叉、变异)的概率运算形成新的群体; (5)并判断所得群体是否满足上层迭代停止准则,满足则输出结果为模型最优解,输出上、下层目标函数值和各节点电压,不满足则回到步骤(3)继续迭代。 采用IEEE-33节点主动配电网系统,如图3所示,在该系统中拥有33个节点,32条支路,主动配电网系统中包含有4个电压等级不同的分布式电源,分布式电源主要包含风机和光伏,每个微电网装机容量为 0.5 MW。系统中划分3个微网区域作为下层优化调度区域,其余部分作为上层优化调度区域,微网区域中含有常规负荷和柔性负荷,上层优化区域中仅含有常规负荷,支路数据和节点数据参见文献[19]。 图3 IEEE-33节点图Fig.3 IEEE-33 node diagram 从表1可以得出,主动配电网引入可转移负荷优化调度的时候,整个调度周期内主动配电网系统的运行成本随着可转移负荷转移率的增加而下降。主动配电网系统优化之前系统的购电成本和系统网损成本分别为11 260.88元和1 905.90元,通过负荷的转移对主动配电网进行优化调度之后,主动配电网系统购电成本和系统网损成本依次降低为8 912.73元和1 742.24元;由于用户部分负荷由峰时段转移到谷时段,导致谷时段对于分布式电源需求增大以至于分布式电源发电运行成本,分布式电源的发电运行成本由1 875.30元上升到2 152.79元,上升了14.80%;可转移负荷调度成本随着转移率的增加而逐渐增加,当转移率为20%的时候可转移负荷的调度成本是850.02元。通过该调度周期对主动配电网的优化调度,整个系统运行成本由23 171.47元下降到20 288.83元,下降了14%。 表1 主动配电网总运行成本单位:元Tab.1 Total operating cost of active distribution network (Unit: Yuan) 如图4所示,早、晚高峰时段的负荷转移到谷时段,使得负荷曲线波峰明显的出现下降,波谷负荷上升。由此可得可转移负荷的实质就是把电价较高的峰时段负荷转移到电价较低的谷时段,降低用户生产用电成本,也降低了电网的运行成本,减轻电网尖峰负荷的压力。 图4 可转移负荷优化调度前后负荷曲线Fig.4 Load curve before and after optimized dispatchable load transfer 如表2所示,在整个调度周期中可中断负荷参与到调度之前主动配电网系统购电成本为11 260.88元,分布式电源发电运行成本为1 875.30元,主动配电网的网络损耗成本为1 905.90元,微网区域总的运行成本为8 129.91元,整个主动配电网运行成本为23 171.99元;当可中断负荷引入主动配电网的优化调度之后,随着中断率的不断上升,系统购电成本、分布式电源发电运行成本、系统网损、微网区域总的运行成本和主动配电网总的运行成本均逐渐下降,随之也产生相应的负荷调度成本,这是由于对中断负荷的用户经济补偿的费用。从表格可以得出并不是负荷中断量越大,整个主动配电网的运行成本就会最低,当可中断负荷中断率为20%的时候微网区域总的运行成本和整个主动配电网的系统的运行成本均达到最低值,分别为7 434.43元和21 049.78元,此时则为主动配电网最优的运行状态,主动配电网在该调度周期内运行成本降低了10.08%。 表2 主动配电网运行成本单位:元Tab.2 Active distribution network operating costs (Unit: Yuan) 如图5所示是主动配电网引入可中断负荷进行优化调度前后的负荷曲线对比。将可中断负荷引入主动配电网时候,中断了用户在峰时段的部分负荷,导致负荷曲线在峰时段出现了明显的下降,负荷曲线也变得更平缓。 图5 可中断负荷优化调度前后负荷曲线Fig.5 Load curves before and after interruptible load optimization 文章中上层规划模型采用遗传算法求解,下层规划模型采用模拟退火算法求解,构建遗传算法与模拟退火算法的混合求解模式,能够有效的降低单一算法求解的复杂程度。 算例分析表明: (1)针对含有柔性负荷的主动配电网的多目标优化特点,并加入大量的分布式单元的情况下,以典型的ADN馈线系统为例和经济调度的宗旨,建立了含有柔性负荷的二层优化调度模型;构建遗传算法和模拟退火算法的混合算法求解流程; (2)对柔性负荷的合理分类和调度使得主动配电网更灵活可调节,降低主动配电网运行成本,分析了柔性负荷不同调度量对系统运行成本的影响。4 算例分析

4.1 可转移负荷对系统影响分析

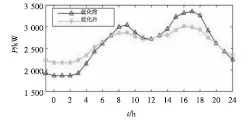
4.2 可中断负荷对系统影响分析

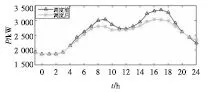
5 结束语
