时变相量下基于陷波滤波算法的下垂控制方法改进*

魏卿，吕智林 ，许柳，孟泽晨

(广西大学 电气工程学院，南宁 530004)

0 引 言

在孤岛微网中，可再生能源的利用越来越普遍，逆变器的控制方式决定了微电网运行的特点，与传统主从控制方式相比下垂控制因其弱通信以及高冗余特性成为时下研究的热点[1-4]。

下垂控制环节中频率的偏差和电压幅值的波动都会受功率的影响，并且单相或三相不平衡系统中功率的获取通常夹杂着不同频率的纹波，因此在功率控制外环中通常会引入一阶低通滤波器(LPF)来滤除纹波。但是由于低通滤波器存在低频极点，影响整个系统的动态特性和稳定性，导致系统响应缓慢甚至出现振荡。基于此文献[5]在下垂方程中引入PI环节，但PI环节的引入会使系统下垂特性变差。文献[6-7]将一阶低通滤波器替换为一个基本周期内对电压电流的积分环节。文献[8]提出了新的滤波方法，但存在系统鲁棒性不强的问题。

下垂控制器的设计通常是基于分布式线路的准静态模型进行小信号稳定性分析[9]。然而准静态模型下的近似忽略了电网电路元件中的动态特性，即认为电压和电流相量变化缓慢。根据准静态下的小信号模型选择控制参数，不符合实际系统的动态变化过程，因此需要更为准确的小信号模型作为选择合适下垂参数的指导。文献[10]建立了相对完整的微电网动态相量模型。文献[11]将时变相量的建模方法应用于逆变器并联系统的小信号建模中，该模型能够较好的反映出系统对扰动的动态过程，但是文献[11]在下垂控制功率环中采用的仍是传统的一阶低通滤波算法。

为更好的描述系统的暂态过程和获得高质量的功率波形，引入陷波滤波器(notch filter)，同时建立陷波滤波算法下的时变相量下垂控制小信号模型，来精确选择稳定范围内的下垂参数，仿真和实验结果验证时变相量模型的准确性和陷波滤波器引入的有效性。

1 下垂控制在两种相量下的比较

逆变器等效电路如图1所示。

图 1 逆变器等效电路Fig.1 Equivalent circuit of an inverter

传统下垂控制功率计算可表示为：

其有功和无功功率可分别表示为：

式(1)中的复功率S是建立在“准静态”相量基础之上，忽略了时变量的暂态影响。文献[12]给出了三相正弦信号e(t)的时变相量表示形式：

P(e(t))代表时变量e(t)向时变相量的转化，e(t)的导数用时变相量可表示为：

则图1中逆变器系统等效模型由式(5)可得：

(6)

此时功率可表示为：

对式(7)、式(8)在平衡点(E,U,δ)处线性化得：

(11)

(12)

为了和时变相量对比，将式(2)、式(3)线性化，同时考虑上述条件得到“准静态”相量下的解耦形式：

在Δδ，ΔU单位阶跃信号输入作用下，通过对比两种小信号模型下的响应(图2)可得在相同条件下时变相量模型能精确拟合系统实际的动态响应，即传统“准静态”相量下的模型不能准确描述系统的暂态过程。(ω=100π rad/s，E=230 V，Z=0.2 Ω,X/R=10, Δδ=0.2, ΔU=5)

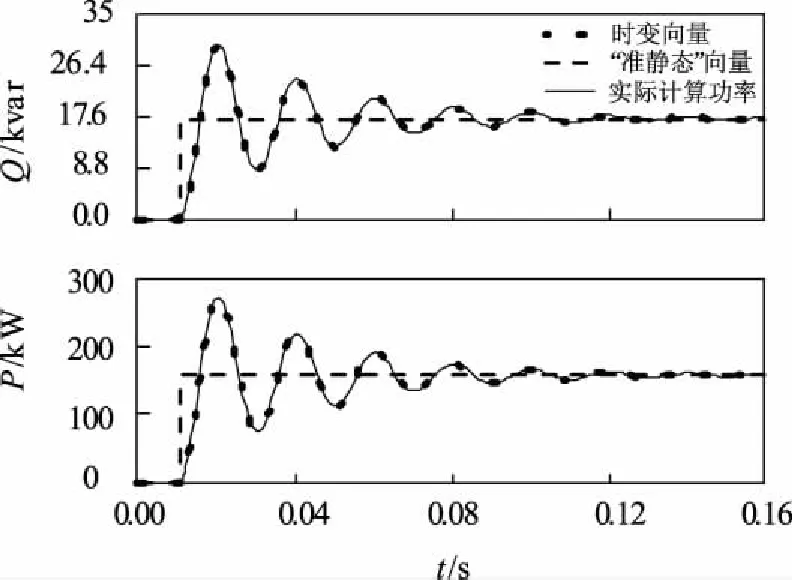
图 2 ΔP和ΔQ对相角Δδ和ΔE变化的阶跃响应Fig.2 Response of ΔP and ΔQ to a step change of Δδ and ΔE

2 下垂控制中改进的滤波算法

传统下垂控制结构如图3所示，通常在功率外环引入一阶低通滤波器见式(15)，来滤除高频干扰波，间接为电压外环提供平稳的参考信号，获取良好的控制效果，由于一阶低通滤波器存在低频极点导致功率带宽有限，影响整个系统的稳定性和动态性能，使系统响应缓慢甚至产生振荡。

基于此引入“陷波”滤波器：

传统的一阶低通滤波器由于低频极点而带宽受到限制，因此必须在响应速度与纹波抑制之间做出权衡，实际上高的截止频率响应速度会更快，但纹波抑制效果相对较差。陷波滤波器在一阶低通滤波器的基础上引入了带有两个极点和零点的二阶传递函数，因此在不扩大纹波范围的基础上提高了系统的动态特性。并且由于下垂控制是基于频率的有差调节，纹波的频率会随负荷的改变而改变，为确保整个频带内存在一个合适的纹波衰减值，滤波器品质因素Q需要进行合理的设置，在陷波滤波器F2(s)中，通过调节ξ1，ξ2的值可以轻易的实现，而一阶低通滤波器则不具备上述优点[11]。文中一阶低通滤波器截止角频率ωc选为31.416 rad/s，陷波滤波器的角频率参数ωc′和ωn分别为94.247 8 rad/s与628.318 5 rad/s，图4中陷波滤波器在中心频率100 Hz处的增益为-67.5 dB，而一阶低通滤波器在此处的增益仅有-26 dB，所以高频纹波在陷波滤波器下衰减更加迅速，滤波效果更为理想。

图 3 下垂控制结构图Fig.3 Structure diagram of droop control

图 4 两种滤波器下的伯德图对比Fig.4 Bode plot comparison between F1 and F2

3 时变相量与“准静态”相量模型的建立

感性系统下，下垂控制方程为：

ω=ω*-mP

(17)

E=E*-nQ

(18)

对式(17)、式(18)线性化经陷波滤波器可改写为：

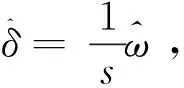
同样为了对比将式(13)、式(14)代入式(19)、式(20)可以得到 “准静态”相量下的δ-P，U-Q闭环特征方程：

(23)

(24)

4 仿真分析

4.1 时变相量与“准静态”相量小信号模型的稳定性分析

利用Matlab画出两种相量模型随下垂系数m,n变化的根轨迹，从而分析下垂系数的选取对系统稳定性的影响，进而得出两种模型的差异，电气仿真参数如表1所示。

表1 逆变器仿真参数表Tab.1 Simulation parameters of inverter

由于式(21)～式(24)的特征值分别受m和n分别影响，因此需要分别来讨论。

(1)有功功率下垂系数m的影响

图5是时变相量与“准静态”相量小信号模型在m变化下的根轨迹。

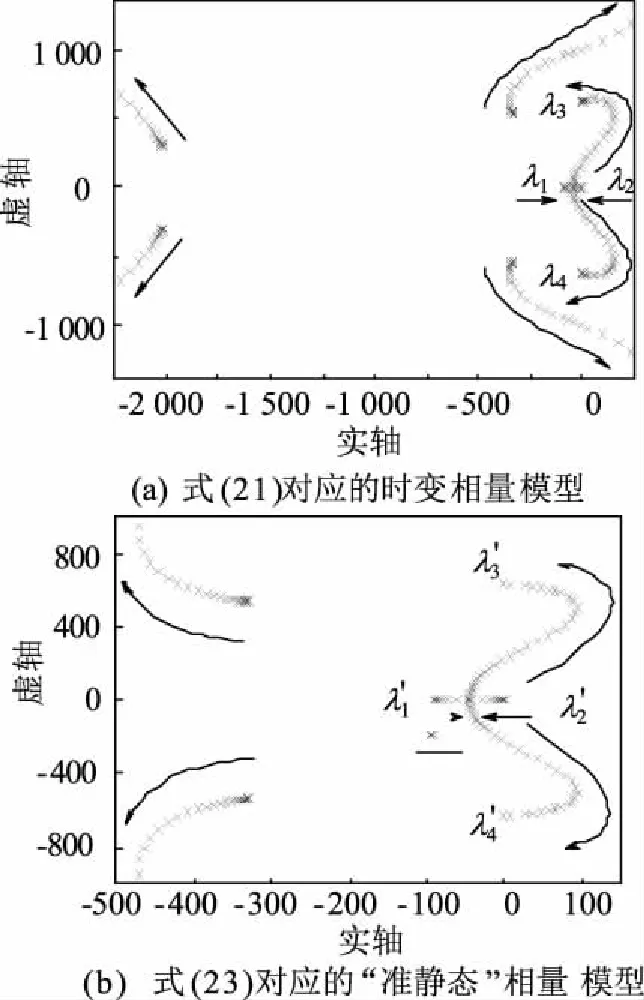
图 5 m变化时对应的根轨迹Fig.5 Root locus for varying m

系统的特征根分布在高、中、低三个频域，其中高频和中频特征根因距虚轴较远而衰减迅速对系统稳定性影响不大，这里主要分析低频特征根。低频下两种相量模型均具有4个特征根，分别为时变相量下两个实根λ1，λ2和一对共轭虚根λ3，λ4；“准静态”相量小信号模型下两个实根λ1′，λ2′和一对共轭虚根λ3′，λ4′，随着m的增大λ1，λ2与λ1′，λ2′分别沿箭头方向变成一对共轭根后向正实部平面运动，其中在图5(a)中λ1，λ2在m≥0.000 752时进入正实部平面，最终共轭根与虚轴相交于点λ3，λ4；图5(b)中λ1′，λ2′在m≥0.001 15时进入正实部平面不稳定区域，最终与虚轴相交于点λ3′，λ4′，所以系统在m=0.000 752时仍处于稳定状态，此时的振荡频率为30 Hz，超调量为78%，因此可以得出当0.000 752≤m≤0.001 15时，对于“准静态”小信号模型来说特征根位于稳定的左半平面，而在时变相量模型下特征根位于不稳定的右半平面。

图6为m取0.000 9时，按照图3搭建Simulink仿真模型后系统输出的有功功率波形，可以看出虽然参数取值在“准静态”模型下系统是稳定的，但实际仿真结果表明系统有功功率出现振荡并发散，系统是不稳定的。

图 6 m=0.000 9时逆变器输出的有功波形Fig.6 Output active powers of inverter whenm=0.000 9

(2)无功功率下垂系数n的影响

图7是时变相量与“准静态”相量小信号模型在n变化下的根轨迹。低频下两种小信号模型的特征根有5个，两对共轭复根，一个实根。图7(b)中准静态相量小信号模型下所有特征根均位于左半平面，无论n怎么变化系统均处于稳定状态，而图7(a)中时变相量小信号模型下随着n的增大，共轭根处于稳定区域但实根λ则向正实部平面运动，在n≥0.035时进入正实部平面，系统将不稳定。

图 7 n变化时对应的根轨迹Fig.7 Root locus for varying n

图8为n取0.04时，搭建Simulink仿真模型后系统输出的无功功率波形，仿真结果表明系统无功功率出现振荡，系统处于不稳定状态。

图 8 n=0.04时逆变器输出的无功波形Fig.8 Output active powers of inverter when n=0.04

通过分析可以得出，“准静态”模型下的根轨迹基本处于左半平面的稳定区域，而在时变相量模型下如果m,n的取值不适当，则会超出稳定区域，这是由于传统小信号模型的建立是在平衡点附近较小范围之上，“准静态”模型下的稳定参数往往不能满足实际系统的动态调节，即“准静态”模型下的稳定范围被扩大。因此使用时变相量模型可以更大程度上考虑暂态过程影响，选取下垂参数更加精确。

4.2 基于两种滤波算法下系统功率波形的分析对比

根据时变相量下的根轨迹选择合适的下垂系数m=0.000 268,n=0.002 53在这组参数下式(21)有3对共轭复根分别为λ1,2=-2030.8±j330.2，λ3,4=-338j±550.5,λ5,6=-27.6±j108.9；式(22)的闭环特征根有6个其中两对共轭根为λ1,2′=-202.01±j302.4，λ3,4′=-330.3±j535.4，两个实根分别为λ5′=-6.4，λ6′=-86.1，此时系统特征根均位于左半平面的稳定区域。

为了对比验证两种滤波算法的纹波抑制效果，在Matlab/Simulink中根据图9微电网拓扑结构和表1中电气参数搭建系统的仿真模型，仿真过程为两台容量均为3 kVA的逆变器分别带相同本地负荷并联运行，其中有功负荷为1.9 kW，无功负荷为1.5 kvar，逆变器1选择陷波滤波算法，逆变器2选择传统的一阶低通滤波算法。

系统在两种滤波算法下有功与无功波形如图10所示，陷波滤波算法要比一阶LPF算法到达稳态的时间快0.1 s，故动态性能更优，并且整个过程中陷波滤波算法得到的功率曲线更加平滑，纹波比传统一阶LPF更小，故采用陷波滤波算法的下垂控制可获取相对平稳的功率波形，从而为电压控制环提供高质量的参考电压，达到理想的控制效果。

图 9 微电网研究案例Fig.9 Case study on micro-grid

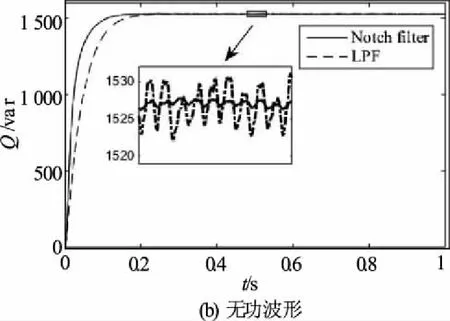
图 10 两种滤波算法下的功率波形Fig.10 Power waveforms under two filtering algorithms

5 实验验证

采用图11的dSPACE实验平台搭建下垂控制系统来进一步验证所提出的改进方法。文中不考虑功率均分问题，单台开关频率为10 kHz三相逆变器即可满足实验要求，考虑到安全及实验条件因素选用额定电压为12 V的三节蓄电池串联作为直流侧恒压电源，滤波电感为2 mH，负载均为三相平衡的阻性负载，其中本地负载为2.2 Ω，投切负荷为5.6 Ω。

图11 实验示意图Fig.11 Wiring diagram of physical experiment

三相PWM互补脉冲信号直接采用dSPACE平台自带RTI(real-time interface)模块DS1104SL_DSP_PWM3产生。信号采样频率为10 kHz，死区时间设为5 μs。为同步PWM与数据采集周期，CPU采用中断的处理方式，实验波形由Control Desk人机界面窗口记录。

实验过程为逆变器启动接上2.2 Ω的本地负载后开始稳定工作，一段时间后并上5.6 Ω的投切负载，最终系统负荷恢复至本地负载。改进后的下垂控制的电压、电流实验波形如图12所示，分析可知由于投切负载时产生扰动，电压经过0.2 s稳定在8 V，电流由4 A增大至5.2 A，系统频率波动在±0.5 Hz内，故改进的方法可以满足下垂控制的要求。

图 12 突变负载时电压和电流实验波形Fig.12 Voltage and current experimental waveforms for sudden load

两种滤波算法下的有功、频率的对比实验波形分别如图13、图14所示。通过分析明显可得所提出滤波算法下的有功和频率波形的毛刺比传统滤波算法下的更小，并且波形过渡平滑。

图 13 两种滤波算法下的有功实验波形Fig.13 Active power experimental waveforms under two filtering algorithms

图 14 两种滤波算法下的频率实验波形Fig.14 Frequency experimental waveforms under two filtering algorithms

综上所述，陷波滤波算法下基于时变相量小信号模型设计的下垂控制器，能够在保证系统稳定的状态下，实现良好的纹波抑制效果。

6 结束语

引入了陷波滤波器分别建立了“准静态”相量和时变相量下的下垂控制小信号模型。准静态相量模型将稳定工作点区域放大，不能反映出系统真实的动态过程，控制参数的选择往往导致系统偏离稳定运行点。通过对两种模型的对比分析可得时变相量小信号模型能更真实反应系统的暂态过程，下垂参数整定更为精确；一阶低通滤波器由于带宽的限制必须在系统响应速度与纹波抑制效果之间做出权衡，仿真和实验表明陷波滤波器的引入使得功率输出波形平滑稳定，纹波波动范围明显减小，同时使系统具有快速的响应速度。