基于QD-SOA级联XGM与XPM波长转换Q因子特性*
2018-09-03密术超王海龙张书玉胡永倩
密术超,王海龙,张书玉,胡永倩,龚 谦
(1.山东省激光偏光与信息技术重点实验室 曲阜师范大学 物理系,山东 曲阜 273165;2.中国科学院 上海微系统与信息技术研究所 信息功能材料国家重点实验室,上海 200050)
0 引 言
全光波长转换器作为一种光学器件,因其可以在全光通信网和密集波分复(DWDM)技术中具有不可替代的作用,始终是国内外广泛关注的焦点。波长转换器能够在两个不同波长上将信息自由转换,并且能够在DWDM技术中实现光波长的转换,实现波长重复利用,提高了波长利用率,同时降低波分复用系统的阻塞率,提高波分复用系统的灵活性和可靠性[1-2]。如今,国内和国外的许多学者已对全光波长转换器进行了广泛探索,如基于半导体光放大器(SOA)的交叉增益调制(XGM)、交叉相位调制(XPM)和四波混频效应(FWM)等利用SOA的多种非线性效应[3-4]。将量子点技术应用于半导体光放大器形成了的量子点半导体光放大器(QD-SOA)。它的一些性质与其他类型的SOA相比具有更突出优势,如更宽的频率带宽、更低的噪声指数、更低的阈值电流、更快的增益恢复和更高的差分增益等[5]。因此,基于QD-SOA实现的全光波长转换器在研究领域受到极大关注[6-8]。本文主要分析了将XGM和XPM两种结构级联在一起,仿真分析了这种结构的波长转换器的Q因子特性,讨论了损耗系数、最大模式增益、注入电流、有源区长度、探测光功率、信号光功率以及电子从激发态ES到基态GS的跃迁时间t21等因素对Q因子的影响,以基于XPM波长转换作为参照对比,同时参考误码率BER(Bit Error Rate)的变化[9],给出了数值模拟的结果。
1 基本原理
1.1 理论模型
QD-SOA的有源区中分布着一定方式排列的量子点。量子点有激发态(Excited State,ES)和基态(Ground State,GS),此外还有浸润层(Wetting Layer,WL)。当电流从外部进入到QD-SOA时,电子最开始进入到能级较高的浸润层,在浸润层中产生大量载流子,然后产生的载流子由浸润层开始向能级较低的激发态跃迁,最后再由激发态向能级最低的基态跃迁。处于基态的载流子与进入到有源区的光子发生辐射放大,最终完成波长转换[10]。在分析QD-SOA的特性时,一般为了方便地描述在基态和激发态中载流子的占有率变化和在浸润层中载流子的浓度变化、增益特性和输出特性,通常采用的是三能级速率方程。能级结构如图1所示[1]。

图1 QD-SOA能级结构
假设QD-SOA为理想状态,忽略三阶非线性极化、群速度色散、ASE噪声和带内效应的影响来简化模型。此时,在浸润层、激发态以及基态载流子的速率方程[11-12]可以描述如下:
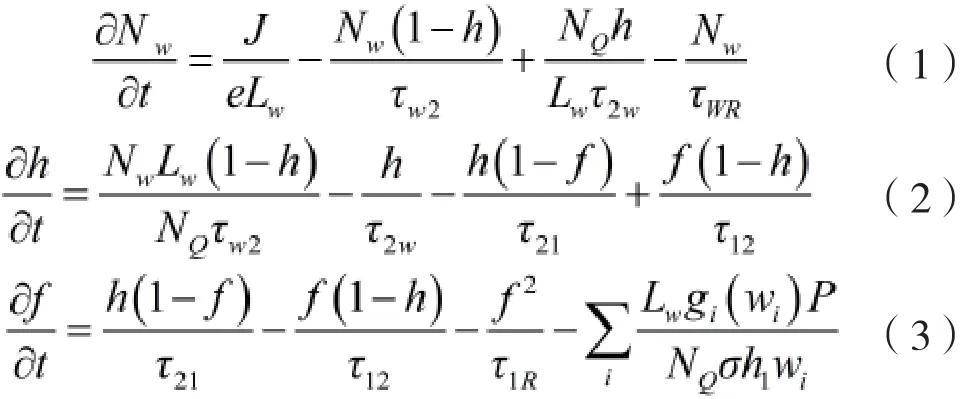
其中,Nw、h和f分别为浸润层中载流子的浓度、基态(GS)中电子的占有几率和激发态(ES)中电子的占有几率;NQ为表面量子点的密度,J和e分别为注入电流密度和电子的电量,Lw为有源区的厚度,τw2和τ2w分别为电子从浸润层到激发态的弛豫时间和电子从激发态到浸润层的跃迁时间,τwR和τ1R分别为浸润层中电子的自发辐射时间和量子点内电子的自发辐射时间,τ21和τ12分别为电子从激发态到基态的跃迁时间和电子从基态到激发态的跃迁时间,gi是模式增益,δ为有源区横截面积,h1wi是光子能量,wi是光的频率。
在QD-SOA中可用下面等式[13]描述输入信号光传播的方程:

其中,Z为信号光在QD-SOA中的传导方向,E+(E-)分别为信号光与传导方向对应的光场强度的正(反)方向,η和Γ分别为波导的线宽增强因子和信号光的光场限制因子,,α 是信号j= ( -1int光的损耗系数。式(4)和式(5)的边界条件是:

1.2 工作原理
图2为基于QD-SOA级联XGM与XPM全光波长转换器的结构示意图。波长为λ1的信号光与波长为λ2的探测光首先经过一个耦合器,通过耦合进入第一个QD-SOA即XGM结构中,完成信号光携带的信息转换到探测光的波长上,同时经过QD-SOA后放大输出转换光λ3。之后,转换光λ3作为第二个QD-SOA的信号光与探测光λ2经过耦合器,通过耦合输入到第二个QD-SOA中,探测光λ2输入到第三个QD-SOA中即XPM结构完成波长转换,输出转换光λ4,最终完成级联XGM和XPM的波长转换。信号光λ1与探测光λ2经过第一个QD-SOA即第一级XGM波长转换中,λ1和λ3波形一一对应单极性相反,在第二级XPM波长转换中,利用XPM的反相转换[14]输出波形,这样输入信号λ1通过波长转换器转换到输出信号λ4上。

图2 基于QD-SOA级联XGM、XPM全光波长转换器结构
在实现级联XGM和XPM的波长转换过程中,把QD-SOA进行细化分段[15],通过牛顿迭代法[16]和四阶龙格-库塔法[17]对QD-SOA进行数值模拟,所选取的部分参数如表1所示[18]。输入信号光和探测光的波长分别为1 500 nm和1 550 nm,脉冲宽度为0.1 ps。如图3所示,当输入信号光λ1为11011时,输出转换光λ4为11011。

表1 基本参数

图3 级联XGM和XPM波长转换前后对比
2 数值模拟
Q因子是波长转换系统的重要指标之一,它的高低决定了信号传输有效性和可靠性。因此,采用Q因子来衡量转换信号的质量。Q因子定义为[19]:

2.1 损耗系数与Q因子的关系
图4为损耗系数α与Q因子和误码率之间的关系。由图4(a)可知,当损耗系数为100时,Q因子为8.85 dB,误码率为4.64×10-19;当损耗系数为200时,Q因子为8.83 dB,误码率为5.07×10-19;当损耗系数为300时,Q因子为8.82 dB,误码率为5.33×10-19。由此可知,增大损耗系数α,Q因子逐渐降低,误码率逐渐增大。由于损耗系数α增大,光信号在通过QD-SOA时所受到的损耗越大,这会导致基态中与载流子发生辐射的光子的数量减小,大大减小了载流子和光子发生辐射的概率,造成Q因子减小,随之误码率增大。与XPM波长转换相比,如图4(b)所示,级联XGM与XPM波长转换的Q因子更高,性能优越。
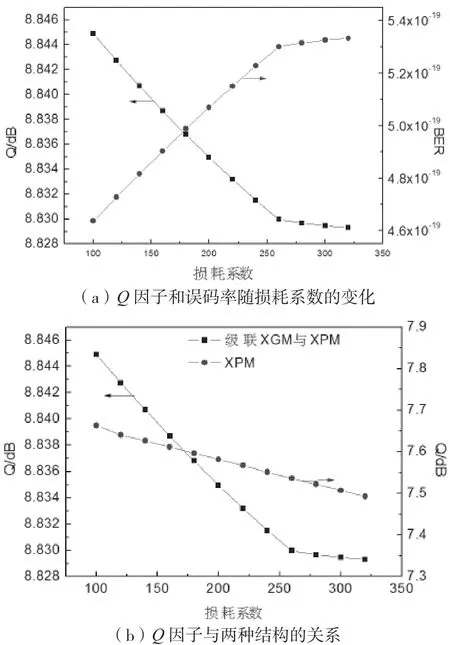
图4 损耗系数与Q因子和误码率的关系
2.2 最大模式增益与Q因子的关系
图5 为最大模式增益gmax与Q因子和误码率的关系。由图5(a)可知,当最大模式增益为1 000 m-1时,Q因子为9.45 dB,误码率为1.68×10-21;当最大模式增益为2 000 m-1时,Q因子为9.10 dB,误码率为4.17×10-21。当最大模式增益为3 000 m-1时,Q因子为8.82 dB,误码率为5.33×10-21。由此可知,随着最大模式增益gmax增大,Q因子逐渐减小,误码率逐渐增大。当增大最大模式增益gmax时,相当于增大了QD-SOA中的光增益,增加了有源区中光子和载流子发生辐射的速率,而基态中由于发生辐射被快速消耗的载流子不能及时得到补充,造成Q因子降低,误码率随之增大。与XPM波长转换相比,如图5(b)所示,级联XGM与XPM波长转换的Q因子更高,性能优越。

图5 最大模式增益gmax与Q因子和误码率的关系
2.3 注入电流与Q因子的关系
图6 为注入电流I与Q因子和误码率的关系。由图6(a)可知,当注入电流为30 mA时,Q因子为8.81 dB,误码率为5.91×10-19;当注入电流为40 mA时,Q因子为8.83 dB,误码率为5.33×10-19;当注入电流为50 mA时,Q因子为8.84 dB,误码率为5.04×10-19。由此可知,随着注入电流I的增大,Q因子逐渐增大,误码率逐渐减小。这是由于随着注入电流的加大,进入QD-SOA有源区中的电子越多,在浸润层中产生的载流子的数量逐渐变大,向基态跃迁的载流子越多。因此,在基态中由于发生辐射被快速消耗的载流子能够及时得到补充,光增益逐渐增大,所以Q因子逐渐增大,误码率逐渐减小。与XPM波长转换相比,如图6(b)所示,级联XGM与XPM波长转换的Q因子更高,性能优越。

图6 注入电流与Q因子和误码率的关系
2.4 探测光功率与Q因子的关系
图7 为探测光功率与Q因子和误码率的关系。由图7(a)可知,当探测光功率为-8 dBm时,Q因子为7.96 dB,误码率为8.40×10-16;当探测光功率为0 dBm时,Q因子为8.83 dB,误码率为7.03×10-18;当探测光功率为-8 dBm时,Q因子为10.78 dB,误码率为2.16×10-20。由此可知,随着探测光功率的增大,Q因子逐渐增大,误码率逐渐减小。如图7(b)所示,探测光功率从-8 dBm增大到8 dBm时,误码率从10-16量级减小到10-20量级,探测光功率对误码率影响很大。因此,探测光功率可以在保证通信质量的前提下灵活选取。
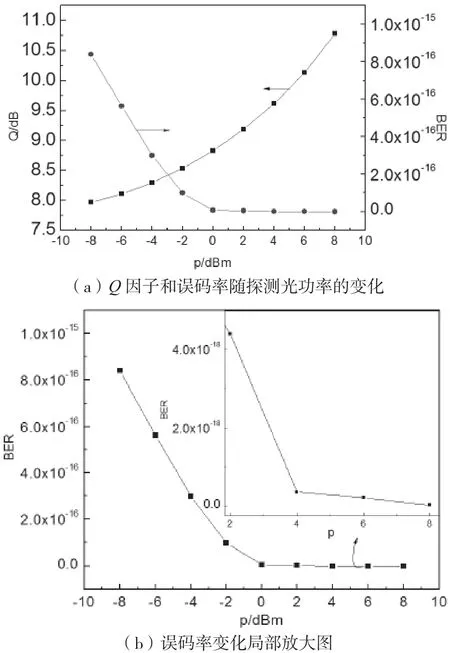
图7 探测光功率与Q因子和误码的关系
2.5 有源区长度与Q因子的关系
图8 为有源区长度L与Q因子和误码率的关系。由图8(a)可知,当有源区长度为1.0 mm时,Q因子为8.34 dB,误码率为3.77×10-17;当有源区长度为1.5 mm时,Q因子为9.88 dB,误码率为1.08×10-18;当有源区长度为2.0 mm时,Q因子为11.23 dB,误码率为5.54×10-21。由此可知,当增加有源区长度时,Q因子增大,误码率减小。这是由于有源区的长度增长,相当于有更多的光子进入有源区,增大了光子与载流子发生辐射的几率,从而增大了光增益,因此Q因子增大,误码率减小。与XPM波长转换相比,如图8(b)所示,级联XGM与XPM波长转换的Q因子更高,性能优越。

图8 有源区长度与Q因子和误码的关系
2.6 信号光功率与Q因子的关系
图9 为信号光功率与Q因子和误码率的关系。

图9 信号光功率与Q因子和误码率的关系
由图9(a)可知,当信号光功率为5 dBm时,Q因子约为9.65 dB,误码率为2.45×10-22;当信号光功率p=10 dBm时,Q因子约为8.83 dB,误码率为5.33×10-19;当信号光功率为15 dBm时,Q因子约为8.01 dB,误码率为5.73×10-16。由此可知,随着信号光功率增大,Q因子逐渐降低,误码率逐渐增大。信号光功率也是Q因子和误码率主要影响参数之一。同时,信号光和探测光功率的选取都对Q因子和误码率影响较大,且对它们影响相反。因此,必须兼顾二者的功率。与XPM波长转换相比,如图9(b)所示,级联XGM与XPM波长转换的Q因子更高,性能优越。
2.7 电子从激发态ES到基态GS的跃迁时间与Q因子的关系
图10为电子从激发态ES到基态GS的跃迁时间t21与Q因子和误码率的关系。
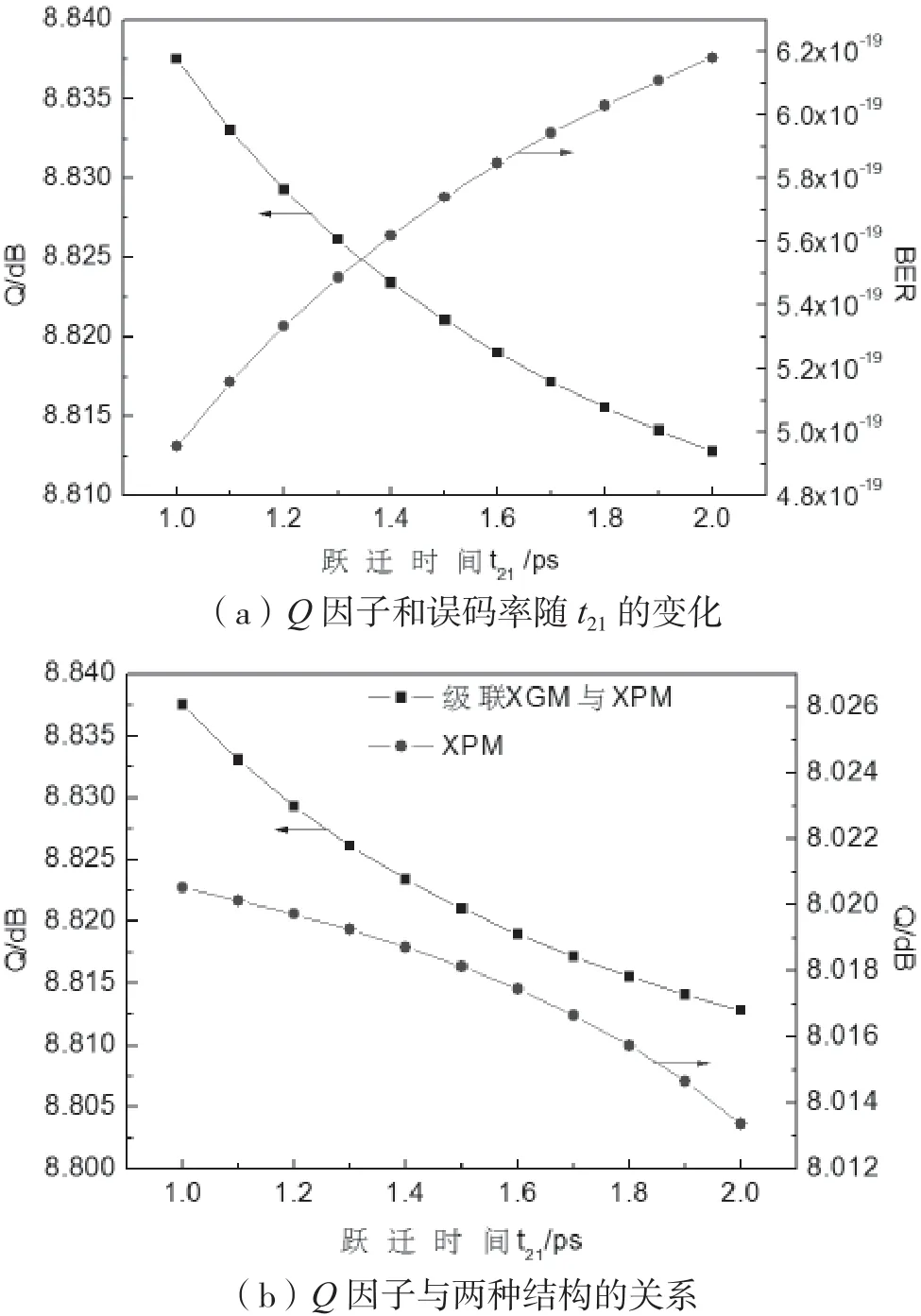
图10 t21与Q因子和误码率的关系
由图10(a)可知,当t21为1.0 ps时,Q因子约为8.84 dB,误码率为4.95×10-19;当t21为1.5 ps时,Q因子约为8.82 dB,误码率为5.74×10-19;当t21为2.0 ps时,Q因子约为8.81 dB,误码率为6.18×10-19。由此可知,随着t21增大,Q因子逐渐降低,误码率逐渐增大。这是由于随着t21增大,电子在激发态的占有率减小,发生辐射的速率降低,光增益减小,造成Q因子逐渐降低,误码率逐渐增大。与XPM波长转换相比,如图10(b)所示,级联XGM与XPM波长转换的Q因子更高,性能优越。
3 结 语
研究基于QD-SOA级联XGM与XPM波长转换Q因子和误码率特性,将基于XPM波长转换作为参照,对比分析了损耗系数、最大模式增益、注入电流、探测光功率、有源区长度、信号光功率、电子从激发态ES到基态GS的跃迁时间等参数对波长转换的影响。结果表明,探测光功率、有源区长度、信号光功率对改善波长转换器的性能和输出信号的质量具有较大的影响,而损耗系数、最大模式增益、注入电流、电子从激发态ES到基态GS的跃迁时间对改善波长转换器的性能和输出信号的质量具有一定的影响:较大的探测光功率和有源区长度;较小的信号光功率能够很好地提高Q因子和降低误码率;基于QD-SOA级联XGM与XPM波长转换器的Q因子高于基于XPM波长转换器,性能更优越。
