多角度论述洛伦兹力做功问题

邓欣宇

(南京市金陵中学 江苏 南京 210005)

洛伦兹力是带电粒子在磁场中运动的驱动力，是研究带电粒子运动规律的基础，正确认识洛伦兹力，对于理解带电粒子在磁场中运动有重要作用．关于洛伦兹力做功高中《物理·选修3-1》中仅轻描淡写地说洛伦兹力总是与粒子的运动方向垂直，不对粒子做功．

但下面的问题中，似乎洛伦兹力又做了功．为了彻底搞清楚洛伦兹力是否做功，本文多角度地进行了论述．

1 问题描述

在空间有竖直方向的匀强磁场，磁感应强度为B，方向垂直纸面向里．在磁场中有一长L,内壁光滑且绝缘的细筒水平放置，筒底部有一质量为m,带正电荷q的小球．现使细管在水平面内以u的速度向右匀速运动．问带电小球离开细筒时其动能增加多少？洛伦兹力所起的作用是什么？

2 受力分析

为了清晰地分析小球的运动，现建立直角坐标系xOy，小球初始静止位置为坐标原点，细管运动方向为x方向，垂直方向为y方向，如图1所示．

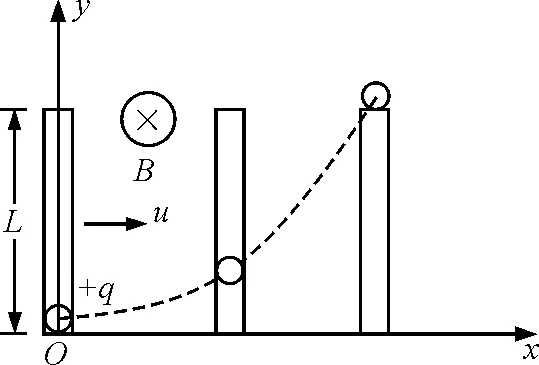
图1 直角坐标系

小球随细管一起沿x正向运动，磁场对运动的带电小球有力的作用，这个力叫洛伦兹力．对于运动的正电荷，洛伦兹力的方向确定是正电荷运动方向与磁场方向所在的平面内，右手四指由正电荷运动方向旋转至磁场方向，大拇指所指的方向即是洛伦兹力的方向．如果是负电荷，大拇指所指方向的反方向即是洛伦兹力的方向．本例中，四指由u旋转至B方向，确立了因u而产生的洛伦兹力f1指向y的正方向．在洛伦兹力f1作用下，小球在y方向运动，速度为v，因v又产生洛伦兹力f2，f2指向x的负方向，如图2(a)所示．

图2 受力分析

本例B和u垂直，洛伦兹力f1和f2的大小

f1=qBuf2=qBv

(1)

由于小球沿x方向做匀速运动，小球在x方向的受力是平衡的，说明细管的管壁对小球有x正方向的弹性力f3，有

f2=-f3

由牛顿第三定律作用力与反作用力关系知道，细管的管壁对小球有x负方向的弹性力，同时细管的管壁受到小球对其x正方向的弹性力f4，如图2(b)所示，有

f4=-f3=f2

(2)

由于细管沿x方向做匀速运动，其x方向受力是平衡的，则细管还要受到外力f5作用

f5=-f4

(3)

由式(2)和式(3)知道，f5=-f2．这说明外力f5与洛伦兹力f2大小相等，方向相反．

上面的分析中出现了两个洛伦兹力，它们与小球运动速度存在“先后”关系，如图3所示.

图3 力与运动的关系

图中可见：力产生了运动，此时力是“母”，运动是“子”，两者相平行．运动产生洛伦兹力，此时运动是“母”， 洛伦兹力是“子”，两者相垂直．

3 运动分析

将x，y方向分别应用牛顿第二定理，得

(4)

小球沿x轴做匀速运动，沿y轴做初速度为零的匀加速运动．

小球离开细管时速度

(5)

小球离开细管时动能增加

(6)

小球运动方程

(7)

消去式(7)中的t，得小球轨迹方程

(8)

这是一个二次函数．

4 做功分析

本文从功的定义、功率、力与速度关系及运动轨迹4个角度分析洛伦兹力做功情况．

4.1 功的定义角度

功的定义为W=Fscosθ，一个力做功与否，取决于力和物体在力的方向上发生的位移，与力的名称、性质无关．对于本例中，在洛伦兹力f1的方向上，小球有位移，所以洛伦兹力f1对小球是做功的．f1大小不变，在小球离开细管时，其位移为L．f1做功

Wf1=f1L=qBuL

(9)

洛伦兹力f2的反方向上，小球也有位移，所以洛伦兹力f2对小球也做功，为负功．f2大小是变化的，f2做功的计算需用积分，在小球离开细管时，f2反方向位移为s.f2所做的功

(10)

洛伦兹力f1与f2做功总和

Wf1+Wf2=0

(11)

洛伦兹力f1与f2做功总和为零．

4.2 功率角度

功率是指力在单位时间内做的功，功率=力×速度．

f1和f2的功率

Pf1=f1v=qBuv

Pf2=-f2u=-qBvu

(12)

所以

Pf1+Pf2=0

(13)

洛伦兹力f1与f2每个时刻功率之和为零，则f1与f2一段时间内做功总和必为零，即洛伦兹力f1与f2做功总和为零．

4.3 力与速度关系角度

图2(a)中f1和f2的合力与u和v的合速度有何关系？

(14)

α=ββ+γ=α+γ=90°

(15)

可见f1,f2的合力与u,v的合速度垂直．也就是说洛伦兹力的合力与小球的合运动方向垂直．所以洛伦兹力的合力对小球的合运动做功为零．

4.4 运动轨迹角度

小球在y方向做匀加速直线运动，y方向速度v满足下列关系

(16)

所以

(17)

对小球轨迹方程式(8)求导，得出

所以

f1dy=f2dx

(18)

Wf1+Wf2=

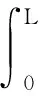
(19)

式中xL是小球在y方向运动的位移L对应的x方向的位移．

以上从4个角度分析了洛伦兹力的合力对小球的合运动做功为零．

4.5 洛伦兹力的作用

既然洛伦兹力的合力对小球的合运动做功为零，那么小球离开细管时动能为什么会增加？下面来解释这个问题．

前面已证明得出外力f5与洛伦兹力f2大小相等，方向相反，f5=-f2．则外力f5在x方向做正功，考虑到式(6)、式(9)和式(11)得

Wf5=-Wf2=Wf1=ΔEk

(20)

说明外力克服洛伦兹力f2，通过洛伦兹力f1做功转化，外力做功转变为小球动能的增加．

也就是说小球动能的增加完全来源于外力做功，洛伦兹力在其中只是起到“二传手”作用，对小球动能的增加没有本质来源作用．

5 结论

(1)细管中带电小球在磁场中随细管做匀速直线运动的同时，还做匀加速直线运动，带电小球运动轨迹为二次函数．

(2)洛伦兹力的合力与小球的合运动方向垂直．

(3) 从功的定义、功率、力与速度关系及运动轨迹4个角度分析得出洛伦兹力的合力对小球的合运动做功为零．

(4)小球动能的增加完全来源于外力做功，洛伦兹力分力做功在能量转换中只是起到“二传手”作用，对小球动能的增加没有本质来源作用．