拉船中几个力学问题

钱树高

(昆明理工大学理学院 云南 昆明 650051)

夏英齐

(云南师范大学物理与电子信息学院 云南 昆明 650500)

在贵刊上一些不同看法的文章[1～3]最初引起我们的注意．我们肯定了文献[3]的正确性，并指出速度合成与分解的基础(依据)在于：运动的合成与分解．又，拉船过程中，绳上点做曲线运动，这也是基于运动的合成与分解，它沿绳运动，又绕定滑轮转动．我们还对文献[1]认为也是不能用速度合成与分解的几个例子，提出了我们的分析与看法[4]．不同的看法、解法、有疑点、有争论,可以明辨是非，对促进学术繁荣是十分有益的．

1 岸上用绳拉湖中船

一人站在岸上以速度v拉绳(或收绳)，或者拉伸跨定滑轮的绳以速度v奔跑，使湖中船靠岸(图1)．求船速V和加速度a．

图1 岸上人拉船示意图

用多种方法可求得到

(1)

若拉绳的加速度为

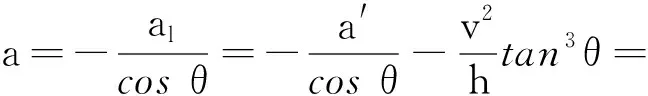
(2)

类似的，拉斜坡上的车(图2)，有同样的关系；

图2 斜坡拉车情形

拉球面上的车(图3)也有

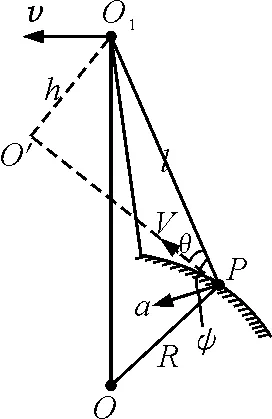
图3 球面拉车情形

还可求得

(3)

2 岸边用绳拉河中船

岸边一人用绳拉河中船靠岸，拉绳速度为v1，水流速度为v2(绳与船在同一水平面上)，求船速和加速度(图4).

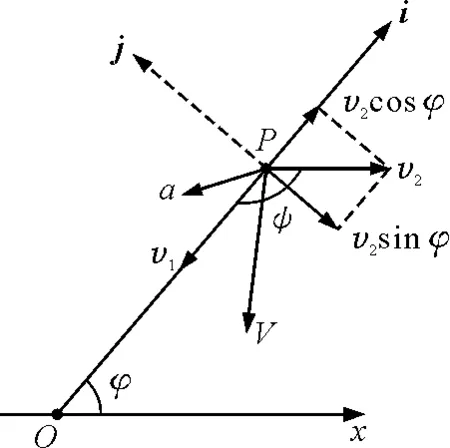
图4 拉河中船靠岸

船的径向速度

船的横向速度

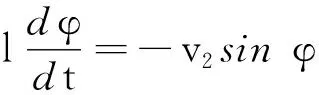
径向加速度

(4)

横向加速度

(5)

3 岸边用二绳拉湖中船

岸边二人分别用二绳拉湖中船靠岸，拉绳速度为v1和v2，相应的绳长为l1和l2，二绳夹角为ψ(二绳与船在同一水平面上)，求船速度和加速度(图5)．

图5 二人分别用二绳拉船

3.1 船的速度和加速度

用做功的观点，可以得到[5]

(6)

由式(6)，得

(7)

于是

(8)

用运动合成与分解的方法，也可求解：从O1(或O2)来看，船的运动可以视为沿绳方向的运动(v1或v2)，和绕O1(或O2)的转动，因此有

及

和上面做功法的结果相同．

对船的加速度也可类似的求解，有

其中沿绳的径向加速度

(9)

(10)

由此即可定出a和θ′.

若匀速拉绳a1=0，a2=0， 此时可求得

tanθ′=

(11)

及

(12)

可以证明，在二绳拉船中，船绕O1转动的角速度ω和角加速度β为

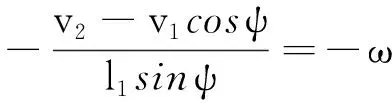
(13)

+(l1v1-l2v2)2cosφ1]=

(v2cosψ-v1)[l1v1+l2v2-(l1v2+l2v1)cosψ]}=

(14)

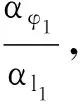
例如，l1=l2(=l),v1=v2(=v)，即对称拉船，可求得

与高h的湖岸上拉船一样，这是很显然的．

另一方面，由式(13)、(14)、(4)及(5)，也可求得上述结果．

又如

用二法都可求得

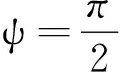
湖船的加速度

而河船的

二者并不相同，应该注意，拉绳或收绳速度不同于河水的作用速度．

3.2 与岸上拉绳之联系

设船约束在圆周上运动(l1=R,v1=0)，如图6所示，这里ψ=∠O1PO2.

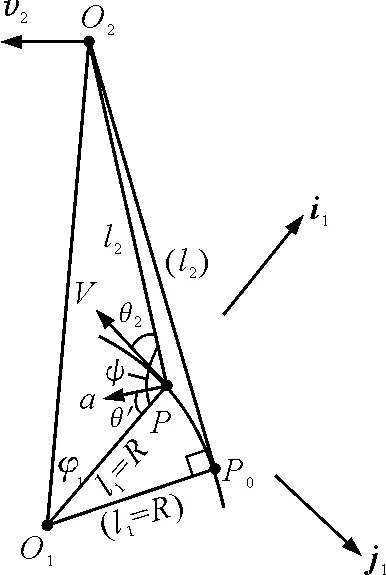
图6 船被约束在圆周上

有

可见

又

由

可得

(15)

及

(16)

还可从另一观点来看，船做圆周运动的向心加速度和切向加速度为

(17)

其中角加速度可由式(14)令v1=0而得

(18)

故

(19)

如果令R→∞(图6)，则球面上圆周变成平面(斜坡或湖面)上一条直线，求得的结果和式(2)是完全一致的．这样，岸上拉船的问题就作为一种特殊情况和二绳拉船完全统一起来了．

可以指出，有些文献说是在“河岸”上“拉河中小船”可能是笔误疏忽[6，7]，也许不是，因此我们还是来照题分析思考一下在河中船的运动，“船向岸靠拢的速度”, 向原点O或岸边靠近的速率是否仍然与湖中小船靠岸的速率相同，读者可自行讨论．