金属分形表面腐蚀过程的数值模拟*

□ 冯 丽 □ 蔡 琦

1.海军工程大学核能科学与工程系 武汉 430033

2.海军上海地区装备修理监修室 上海 200136

1 研究背景

在海洋环境下，金属材料的腐蚀现象日益突出。目前，已有的腐蚀模型大多采用逆向建模方法，即先通过模拟试验方法获得试样腐蚀产物层，再采用扫描电镜、光学显微镜等仪器得到腐蚀图像，最后通过数字图像处理技术对腐蚀图像进行数据分析和评价。然而，腐蚀是材料和环境作用造成的一个缓慢变化过程，具有很大的不确定性和试验环境依赖性。采用正向建模方法，对材料腐蚀损伤过程进行数值模拟，能够避免繁杂耗时的试验过程。目前有少数二维或三维腐蚀模型采用正向建模方法［1-2］，然而所建立的三维腐蚀模型均未考虑材料腐蚀前表面缺陷或粗糙度的影响，而是将材料表面作为平面处理后，这样所得到的数值模拟结果势必与真实表面腐蚀结果存在差异。

笔者首先基于分形理论，采用MATLAB软件编程生成三维分形表面；然后采用三维元胞自动机方法，在模拟分形表面的基础上，对材料在海水中的腐蚀损伤过程进行微观模拟，研究金属腐蚀形貌与分形特征参数之间的关系及变化规律，为腐蚀微观模型的进一步研究提供思路。

2 分形理论

分形理论是研究复杂随机现象的有力工具［3］，目前已有的腐蚀模型多采用逆向建模方法，先通过试验方法得到腐蚀产物层，再应用计算机图像分析与处理技术观察腐蚀表面分形特征，计算腐蚀图像分维指标，用以描述腐蚀过程。笔者采用正向建模方法，应用MATLAB软件编程，采用数值模拟方法直接生成分形表面，在模拟分形表面的基础上，采用三维元胞自动机方法建立腐蚀微观模型，模拟分形粗糙表面在海洋环境下的腐蚀损伤过程，研究腐蚀形貌与分形特征参数之间的关系及变化规律，为考虑表面缺陷或表面粗糙度效应的腐蚀规律和腐蚀机制研究提供思路。

文献［4］对前人提出的二维分形函数进行拓展，由二维空间引入三维空间。文献［5］在前人研究的基础上，得到分形函数的三维直角坐标表达式：

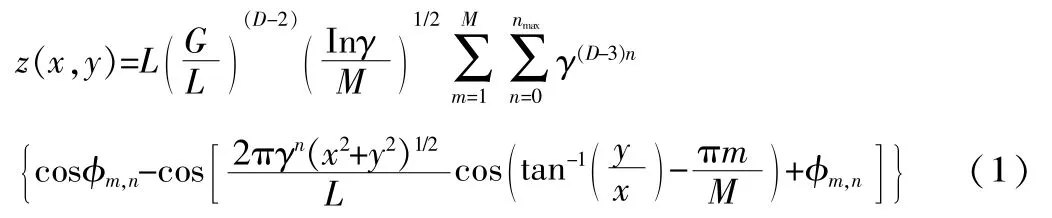
式中：x，y为高度是z的点的直角坐标；D为分形维数，2≤D≤3；G为分形粗糙度；γ为与轮廓谱密度相关的参数，γ＞1；M为叠加峰值数量；φm，n为随机相位；L为取样长度；n为自然数序例；nmax=int［log（L/LS）/logγ］，LS为测量尺度。

由式（1）对随机表面进行模拟，假设G=1.36×10-2nm，M=10，γ=1.5，D=2.8，得到三维分形模拟表面，如图1所示。

3 腐蚀模型

3.1 元胞自动机方法

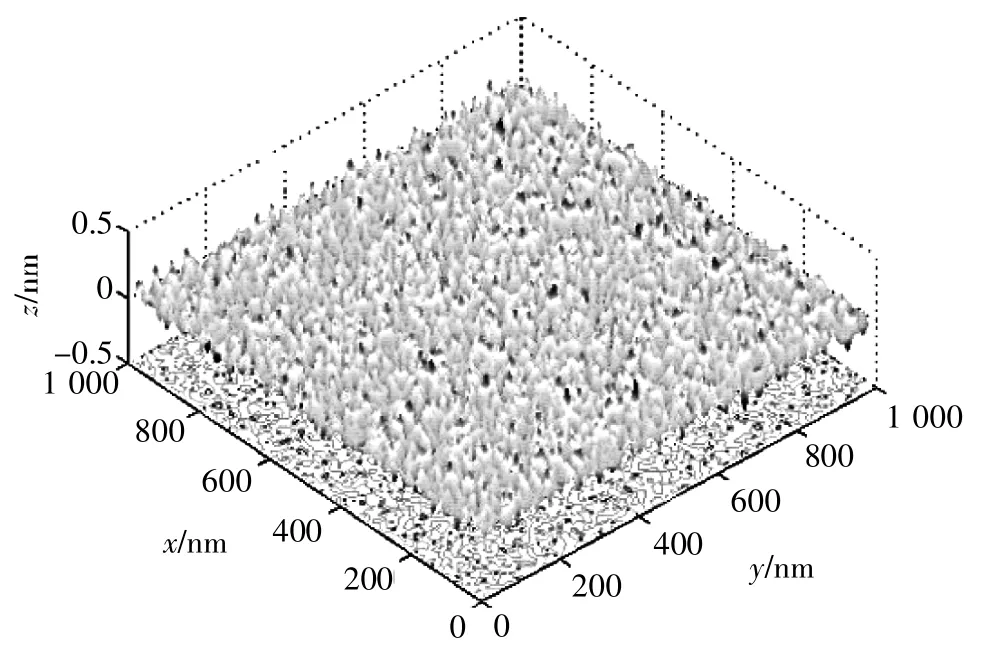
▲图1 三维分形模拟表面

元胞自动机方法可将复杂的空间系统离散为有限的规则的网格空间，从而简化计算。由于三维元胞自动机方法能更真实地模拟实际情况，近年来已有不少研究者采用三维元胞自动机方法来模拟简化一些工程实际情况，如基于元胞自动机方法对材料点蚀过程进行数 值模拟等［6-10］。

笔者在模拟三维分形表面的基础上，采用三维元胞自动机方法对表面腐蚀损伤过程进行微观模拟。由于考虑了表面缺陷或表面粗糙度的效应，因此更符合实际，具有合理性，并对腐蚀过程和机制的进一步研究具有指导意义。

3.2 数值模拟

（1） 应 用 MATLAB编程。选取直角坐标x和y方向的 1 nm×1 nm平面，在x和y方向将 0～1 nm均分为100个网格，再由分形函数生成三维分形表面，此表面作为腐蚀前，即t=0时刻的表面形貌。

（2）应用三维元胞自动机方法。选取1 nm×1 nm×1 nm 立方体，在x、y和z方向将 0～1 nm均分为100个网格，其中-0.5≤z≤0.5， 从而将金属材料和海水系统离散划分为有序的元胞。在模拟系统中考虑三种类型元胞：① 金属性元胞，即金属原子；② 腐蚀性元胞，即氯离子；③ 非腐蚀性元胞，即水分子。

（3）设定边界条件和各相关参数。应用MATLAB编程对每个时间步长进行迭代计算，得到不同时刻金属材料腐蚀前后的表面形貌数据。为了提高计算速度、简化模拟程序，腐蚀模型的计算方法采用文献［11］提出的观点，即在模拟程序运行时，某一时刻只考虑材料与海水界面间相关的元胞。

3.3 实例

程序中各参数取值如下：轮廓谱密度相关参数γ=1.5，表面能ΔG=0.25 J/m2，叠加峰值数量M=10，分形粗糙度G=1.36×10-2nm，分形维数D=2.8，氯离子数量∶水分子数量=40∶60。图2、图3分别显示了腐蚀模型中使用的分形表面和元胞自动机模型网格，图4、图5分别显示了z=0截面腐蚀前后元胞分布，表1列出了不同分形维数和分形粗糙度时金属表面腐蚀前后形貌统计参数，时刻0表示腐蚀前，时刻300 s表示腐蚀后。

无论以何种方式形成的表面，在微观上都不可能是非常平整或光滑的，并且是由许多微观不规则的凸峰和凹谷组成的粗糙表面。凹凸不平的粗糙表面金属原子与海水中的水分子和氯离子接触，氯离子随机分布在海水中，当它与表面金属原子接触，并向金属原子的方向运动时会发生腐蚀现象，氯离子将替换金属原子，金属原子则被腐蚀消耗掉。腐蚀现象发生后，更多的表面金属原子将被腐蚀消耗掉。由数值统计结果可知：G不变时，表面粗糙度值随D增大而迅速减小；D不变时，表面粗糙度值随G增大而增大。

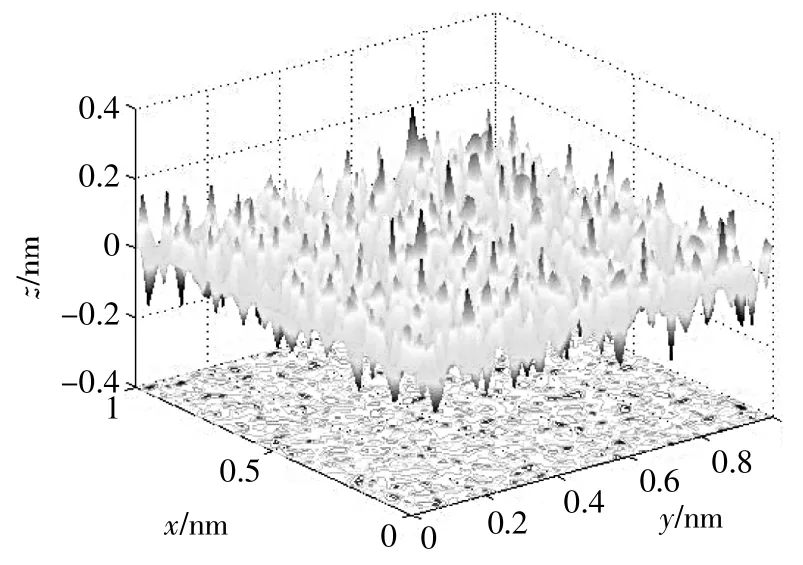
▲图2 腐蚀模型中分形表面

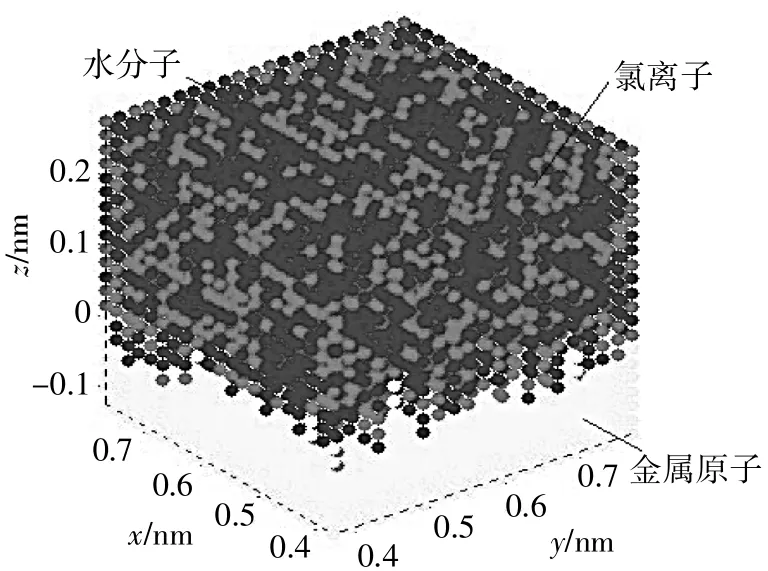
▲图3 元胞自动机模型网格

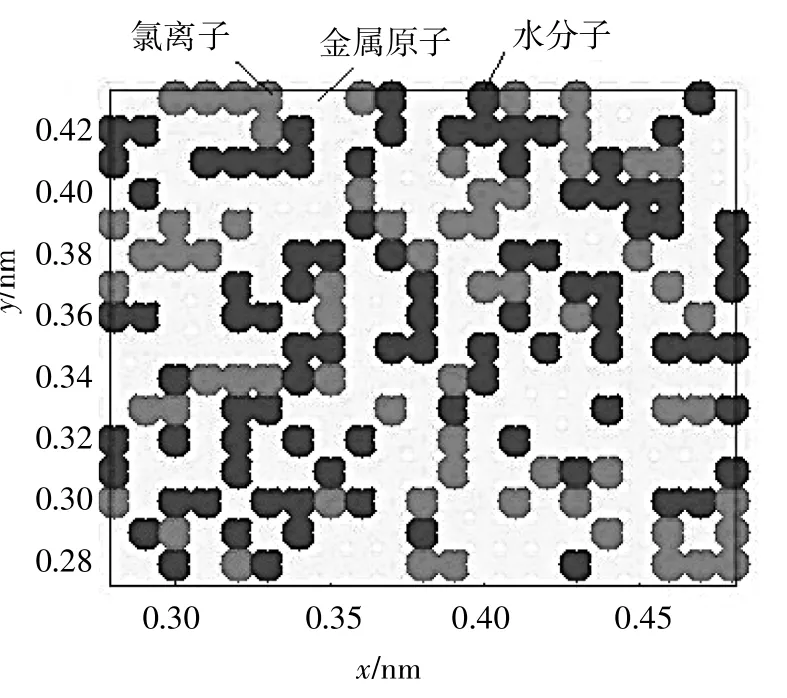
▲图4 z=0截面腐蚀前元胞分布

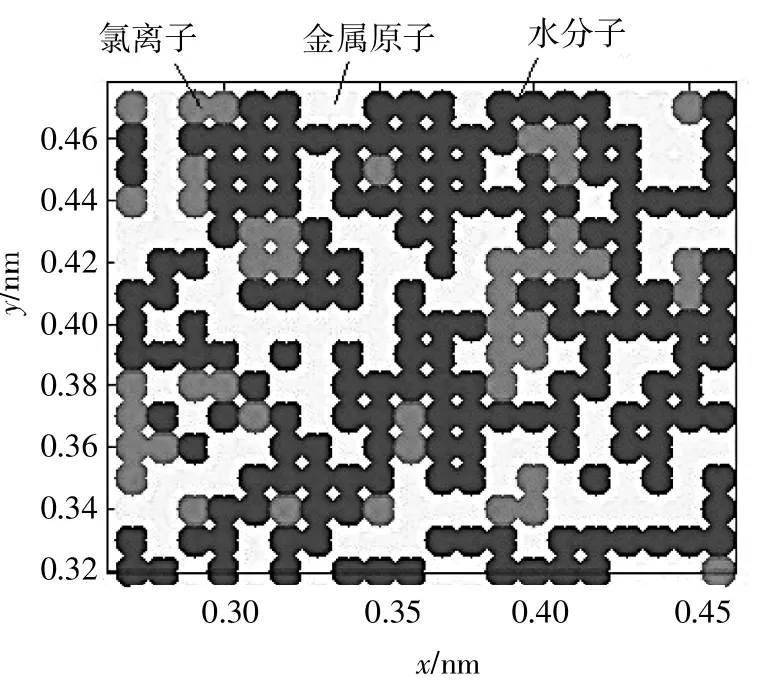
▲图5 z=0截面腐蚀后元胞分布

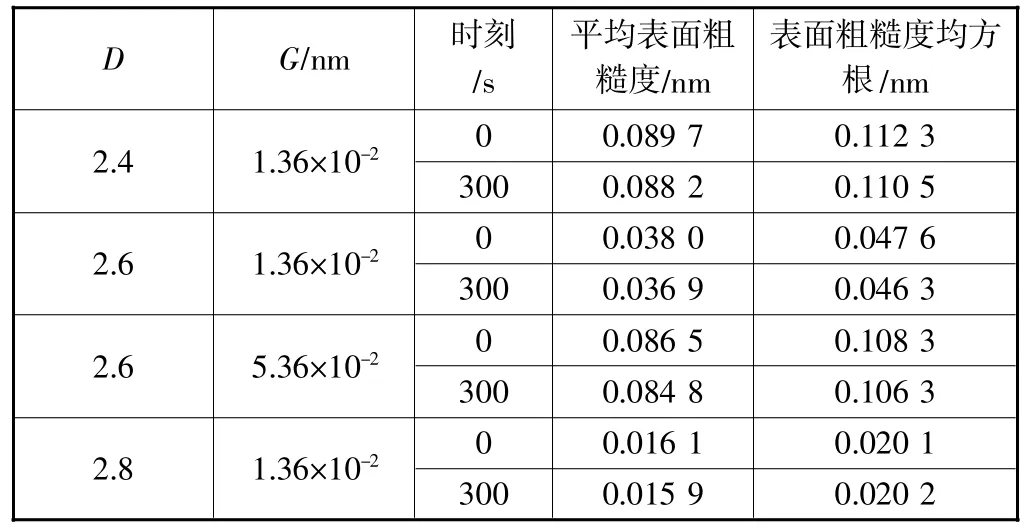
表1 金属表面腐蚀前后统计参数

4 结论

基于分形理论建立腐蚀微观模型，并应用MATLAB编程对分形粗糙表面的微观腐蚀过程进行数值模拟。建立的腐蚀模型为考虑表面缺陷或表面粗糙度效应的腐蚀规律和腐蚀机制研究提供了思路。

由腐蚀后截面上元胞分布可知，金属材料表面发生腐蚀后，部分金属原子被氯离子腐蚀消耗掉，进而被水分子填充，因而表面金属原子逐渐减少，水分子逐渐增多，符合客观规律，同时，证明了所建立模型的合理性。

由金属表面腐蚀前后统计参数：分形粗糙度不变时，表面粗糙度值随分形维数的增大而迅速减小；分形维数不变时，表面粗糙度值随分形粗糙度的增大而增大。